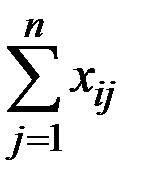Рассмотренная статистическая балансовая модель производства характеризует состояние экономики в данный момент и не учитывает динамику развития народного хозяйства.
Получаемые средние уровни затрат не отражают многообразия возможных технологий, реализацию достижений технического прогресса.
Поэтому на основе межотраслевого баланса нельзя решать задачи экономической динамики, т.е. определять оптимальные темпы и пропорции развития различных отраслей народного хозяйства.
На частичное устранение недостатков статических балансовых моделей направлены динамические модели.
По характеру математической модели динамические балансы представляются в виде системы линейных дифференциальных или разностных уравнений.
В качестве примера рассмотрим динамическую модель, позволяющую учитывать капиталовложения в различные объекты экономической системы, а также связь между общими объектами производства в различные периоды.
Обозначим количество продукции 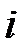 –го объекта, затрачиваемое в данный период на капиталовложения в
–го объекта, затрачиваемое в данный период на капиталовложения в 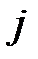 –й объект, через
–й объект, через 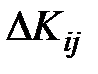 .
.
Номер периода обозначим индексом 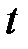 .
.
Тогда балансовая система уравнений (2.3) преобразуется в систему
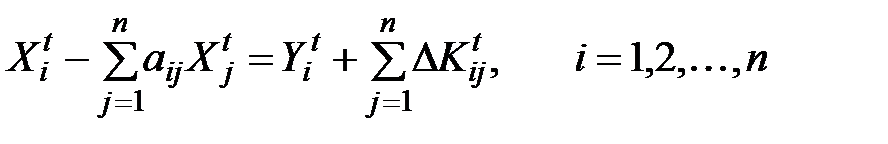 . (2.11)
. (2.11)
Обычно предполагают, что необходимые для объекта капиталовложения пропорциональны приросту продукции объекта, т.е.
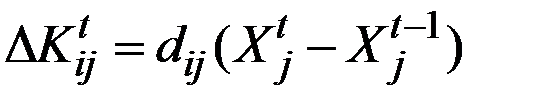 .
.
В результате уравнение (2.11) приводится к виду
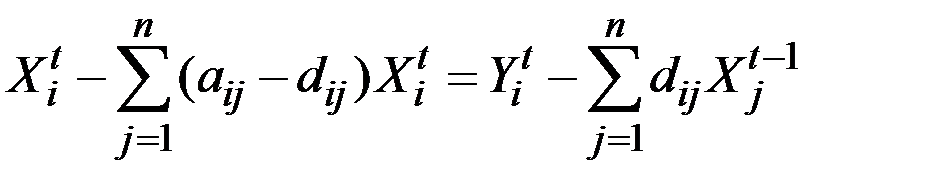 . (2.12)
. (2.12)
Величины 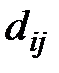 , называемые коэффициентами вложений, позволяют выявить необходимую связь, существующую между периодами.
, называемые коэффициентами вложений, позволяют выявить необходимую связь, существующую между периодами.
Из системы (2.12), зная общие объёмы производства по всем объектам в период 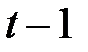 и объёмы потребления, можно найти объёмы производства в период
и объёмы потребления, можно найти объёмы производства в период 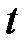 .
.
Такого рода модели учитывают динамику развития экономической системы.
Пример 2.2. Завод состоит из двух основных цехов и одного вспомогательного, каждый из которых выпускает один вид продукции.
Известны (табл. 2.4) расходные коэффициенты (прямые затраты) аi j единиц продукции i–го цеха, используемые как “сырье” (“промежуточный продукт”) для выпуска единицы продукции j–го цеха, а также количество единиц уi продукции i–го цеха, предназначенных для реализации (конечный продукт).
Таблица 2.4
Исходные данные задачи
Цеха
Прямые затраты а ij
Конечный
продукт yi
Определить:
1) коэффициенты полных внутрипроизводственных затрат;
2) валовой выпуск (план) для каждого цеха;
3) производственную программу цехов;
4) коэффициенты косвенных затрат.
Решение. Обозначим производственную программу завода через
Х = (х1, х2, х3),
где хi есть валовой выпуск продукции i–го цеха.
План выпуска товарной (конечной) продукции обозначим через
Y = (у1, у2, у3).
Кроме того, введём матрицу А = ||аi j|| расходных коэффициентов, указанных в таблице.
Тогда производственные взаимосвязи завода могут быть представлены следующей системой трёх уравнений:
х i – (ai1xi + ai2x2 + ai3x3) = yi ; (i = 1, 2, 3),
или в матричной форме
X – AX = Y .
Решение этого уравнения запишется через обратную матрицу:
X = (E – A)–1Y,
где Е – единичная матрица третьего порядка.
Элементы матрицы
(Е – А)– 1 = ||si j||
представляют собой искомые коэффициенты полных внутрипроизводственных затрат.
1) Выполнив необходимые расчёты, получим коэффициенты полных внутрипроизводственных затрат 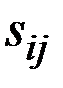
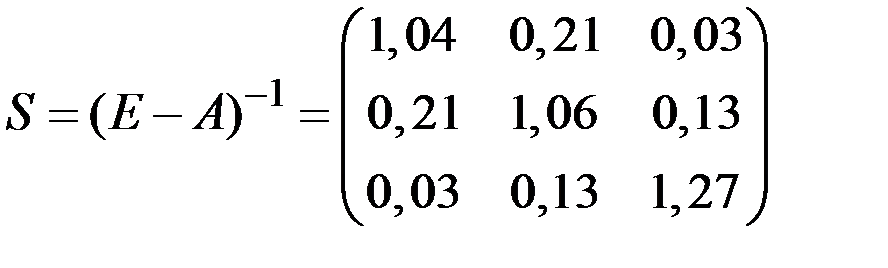 .
.
Таким образом, например, для выпуска единицы конечной продукции 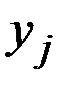 I, II и III цехов необходимо затратить продукции 1–го цеха соответственно 1,04; 0,21 и 0,03 единиц.
I, II и III цехов необходимо затратить продукции 1–го цеха соответственно 1,04; 0,21 и 0,03 единиц.
2) Для определения валового выпуска 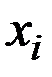 продукции всех трёх цехов воспользуемся равенством
продукции всех трёх цехов воспользуемся равенством
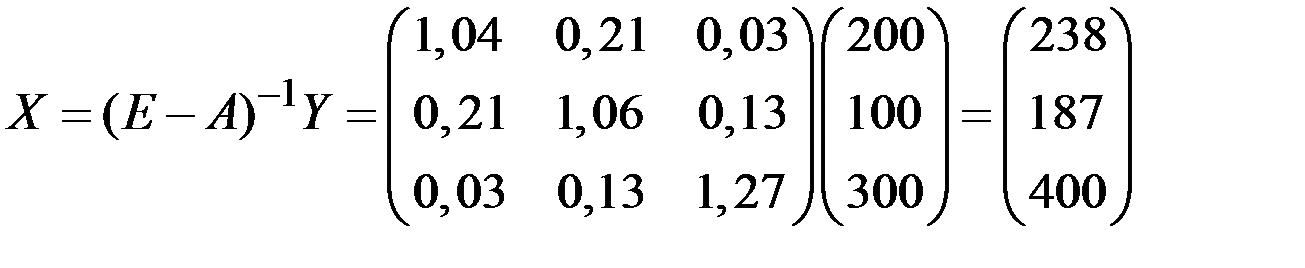 .
.
Следовательно, получим план
х1 = 238, х2 = 187 и х3 = 400.
3) Производственную программу каждого из цехов 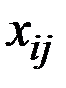 можно определить из соотношения
можно определить из соотношения 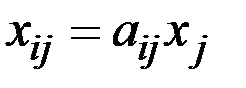
(j = 1, 2, 3; i = 1, 2, 3).
В результате получим следующую таблицу (с округлением) производственной программы завода:
| Цеха | Внутрипроизводственное потребление хij | Итого
| Конечный продукт yi | Валовой выпуск х i | ||
| I | II | III | ||||
| I II III | 0 47 0 | 38 0 19 | 0 40 80 | 38 87 99 | 200 100 300 | 238 187 400 |
4) Коэффициенты косвенных затрат найдём как разность между 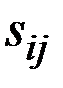 и ai j или в матричной форме
и ai j или в матричной форме
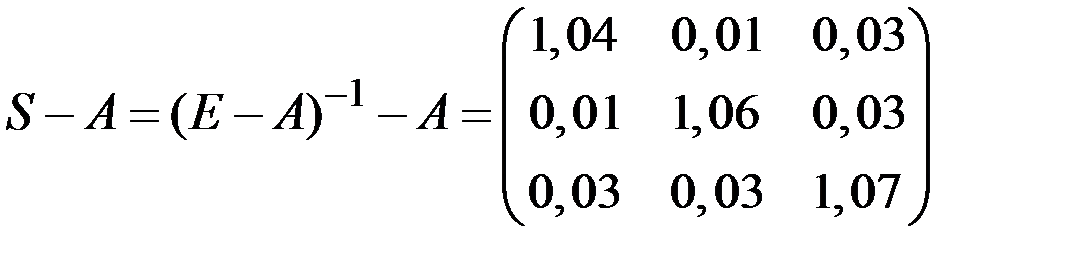 .
.
Пример 2.3. Добавим факторы. Дополнительно к данным примера 2.2 в следующей таблице указаны расходные нормы двух видов сырья и топлива на единицу продукции соответствующего цеха, трудоёмкость продукции в человеко–часах на единицу продукции, стоимость единицы соответствующего материала и оплата за 1чел.–час.:
|
Факторы | Нормы расхода | Стоимость, руб. | ||
| I | II | III | ||
| Сырье «а» Сырье «б» Топливо | 1,4 – 2,0 | 2,4 0,6 1,8 | 0,8 1,6 2,2 | 5 12 2 |
| Трудоёмкость | 10 | 20 | 20 | 1,2 |
Определить: 1) суммарный расход сырья, топлива и трудовых ресурсов на выполнение производственной программы;
2) коэффициенты полных затрат факторов: сырья топлива и труда на единицу конечной продукции каждого цеха;
3) расход сырья, топлива и трудовых ресурсов по цехам;
4) производственные затраты в рублях по цехам и на всю производственную программу завода;
5) производственные затраты на единицу конечной продукции.
Решение. 1) Суммарный расход сырья «а» можно получить, умножив соответствующую 1–ю строку исходной таблицы на вектор X , т.е.
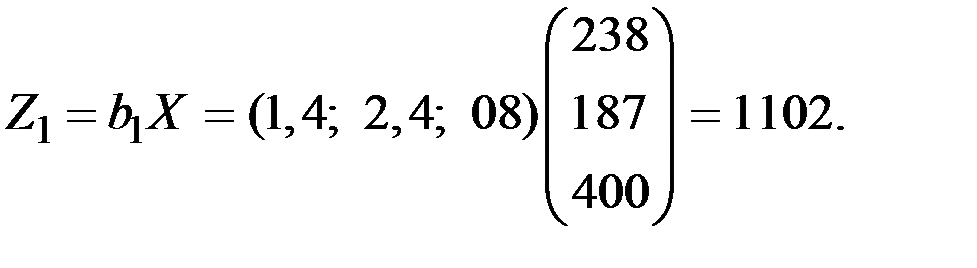
Аналогично можно получить расход сырья «б» и т.д.
Все это удобно записать в виде произведения
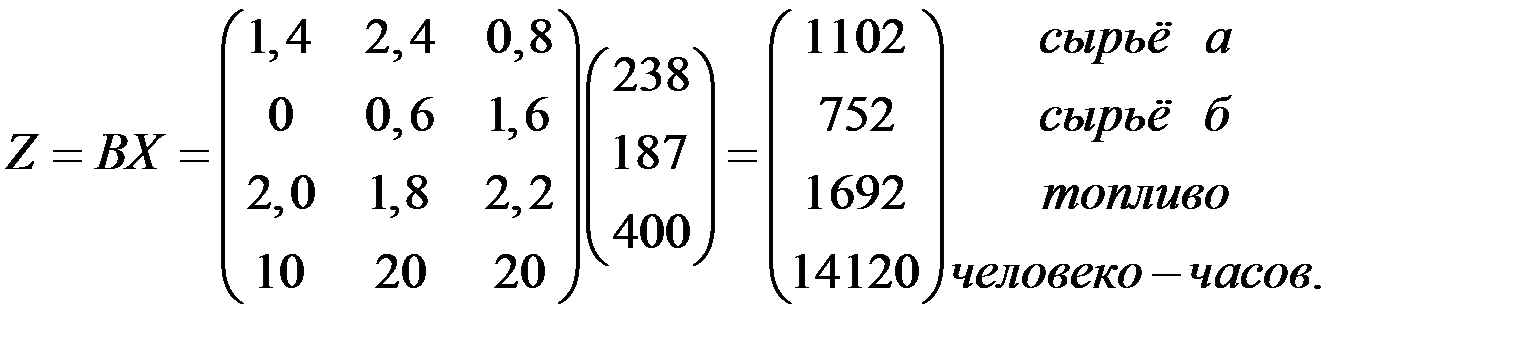
2) Расход сырья «а» на единицу конечной продукции I цеха найдём из выражения
с11 = 1,4s11 + 2,4s21 + 0,8s31.
Следовательно, соответствующие коэффициенты полных затрат сырья, топлива и труда на каждую единицу конечного продукта получим из произведения матриц:
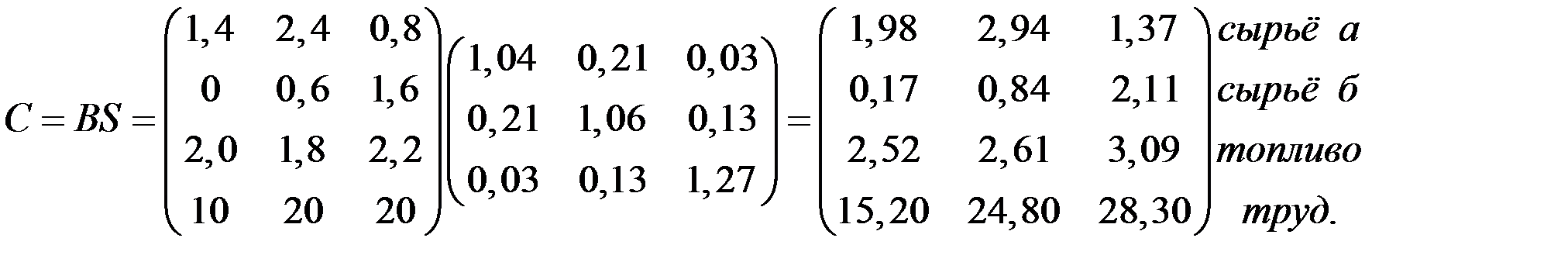
Например, для изготовления у1 = 1 необходимо затратить 1,98 ед. сырья «а», 0,17 ед. сырья «б», 2,52 ед. топлива и 15,2 чел.–ч.
3) Расход сырья, топлива и т.д. по каждому из цехов получим из умножения их расходных норм на соответствующие валовые выпуски по цехам. В результате получим матрицу полных расходов факторов:
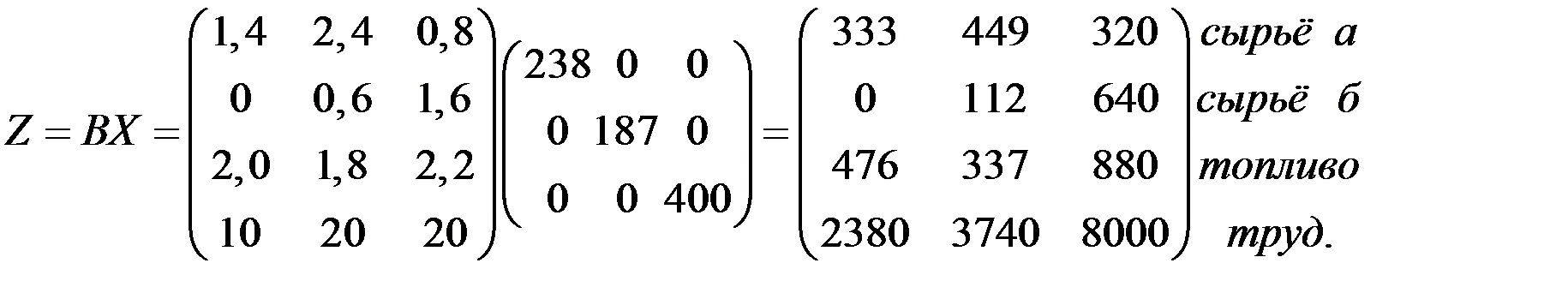
4) Производственные расходы по цехам можно получить путём умножения слева строки стоимостей Р = (5; 12; 2; 1,2) на матрицу Z:
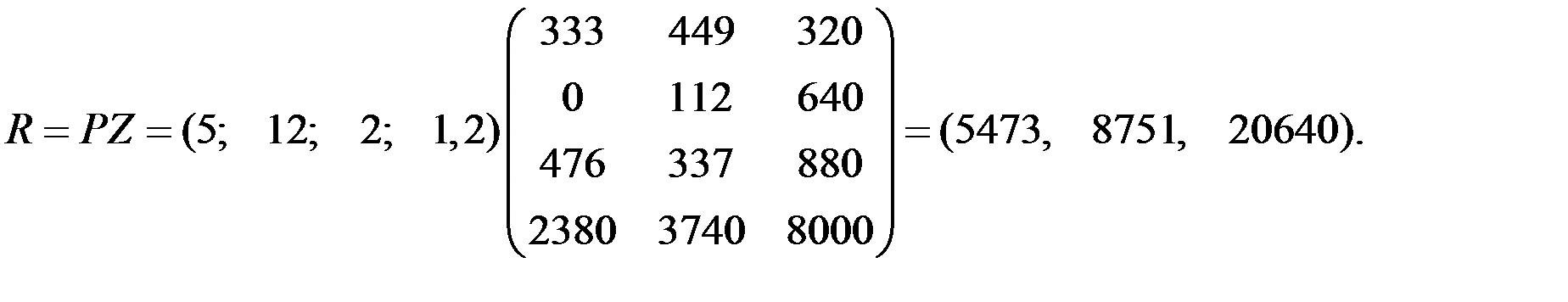
Затраты на всю производственную программу завода составят:
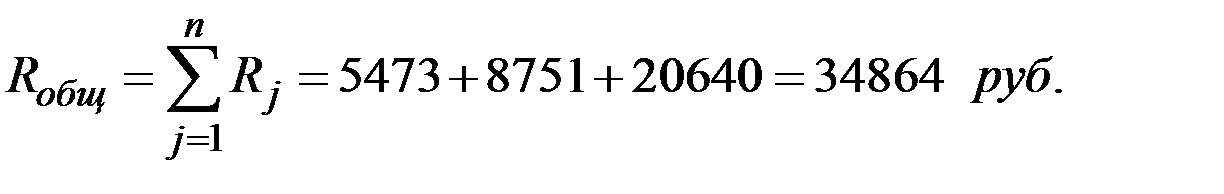
5) Производственные затраты на единицу конечной продукции, необходимые для определения себестоимости продукции, можем найти путём умножения строки цен на матрицу коэффициентов полных затрат факторов:
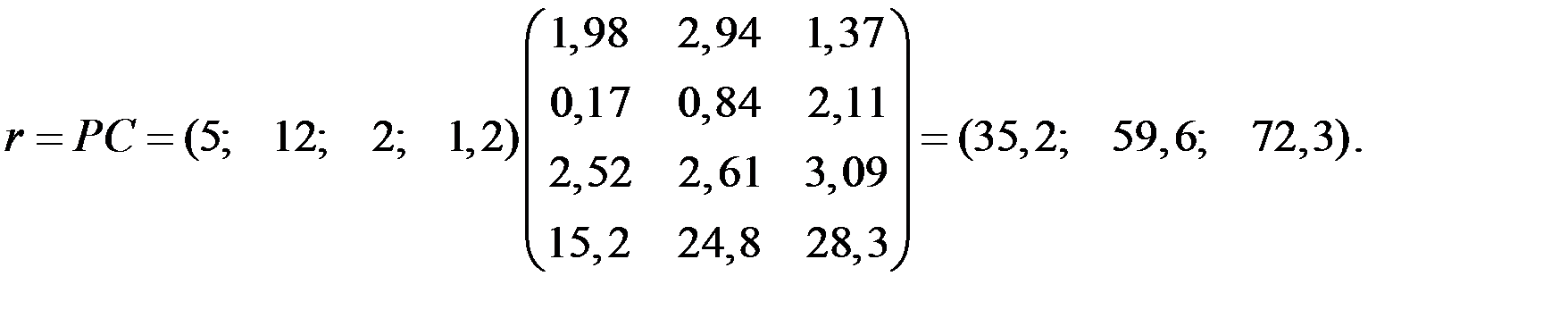
Внутрипроизводственные затраты на единицу товарной продукции I, II и III цехов соответственно составляют: 35,2 руб., 59,6 руб. и 72,3 руб.
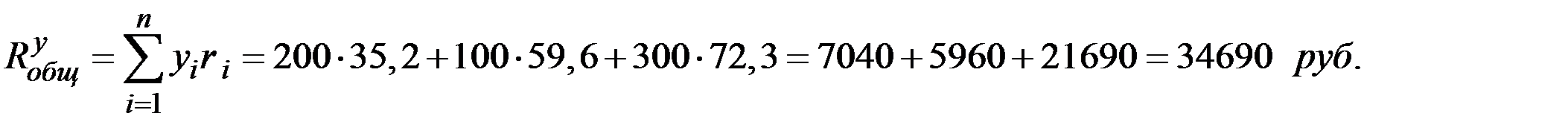
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 2
1. В чём заключаются суть и особенности балансовых моделей?
2. Что такое коэффициенты прямых, косвенных и полных затрат?
3. Как происходит укрупнение балансовой таблицы?
4. Укажите особенности динамических балансовых моделей.
5. Приведите примеры использования балансовых моделей.
Задание 2.1. Предприятие состоит из двух основных цехов и одного вспомогательного, каждый из которых выпускает один вид продукции. Известны расходные коэффициенты (прямые затраты) единиц продукции i–го цеха, используемые как промежуточный продукт для выпуска единицы продукции j–го цеха, а также количество единиц уi продукции i –го цеха, предназначенных для реализации (конечный продукт). Заданы также расходные нормы двух видов сырья и топлива на единицу продукции соответствующего цеха, трудоёмкость продукции в человеко–часах на единицу продукции, стоимость единицы соответствующего материала и оплата за 1чел.–час. Определить:
1) коэффициенты полных затрат;
2) валовой выпуск (план) для каждого цеха;
3) производственную программу цехов;
4) коэффициенты косвенных затрат.
5) суммарный расход сырья, топлива и трудовых ресурсов на выполнение производственной программы;
6) коэффициенты полных затрат сырья топлива и труда на единицу конечной продукции каждого цеха;
7) расход сырья, топлива и трудовых ресурсов по цехам;
8) производственные затраты по цехам и на всю программу предприятия;
9) производственные затраты на единицу конечной продукции.
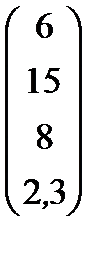
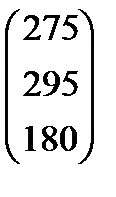
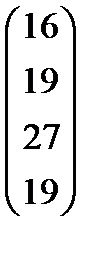
Варианты заданий приведены в табл. 2.8.
Таблица 2.8
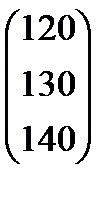
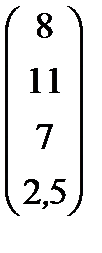
Варианты заданий
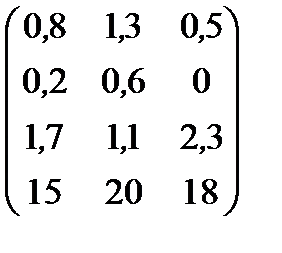
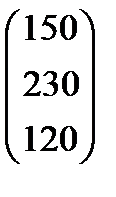
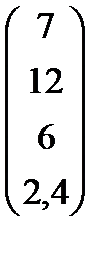
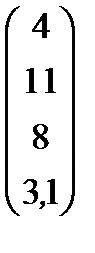
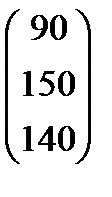
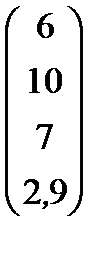
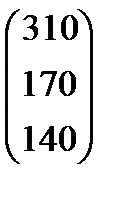
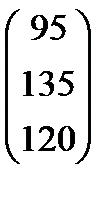
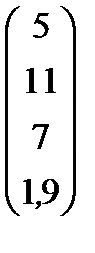
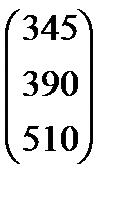
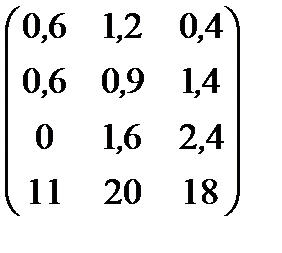
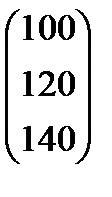
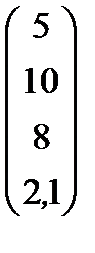
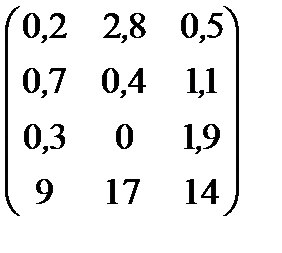
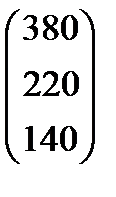
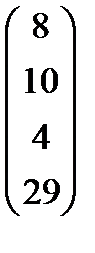
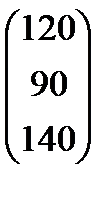
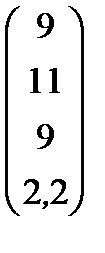
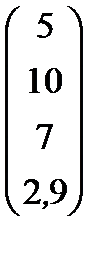
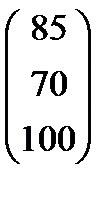
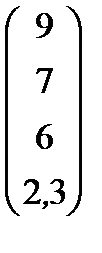
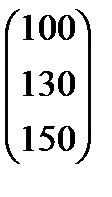
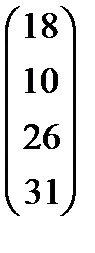
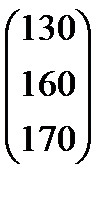
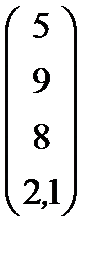
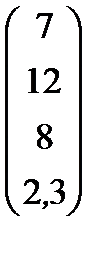
| Номер варианта | Матрица коэффициентов прямых затрат | Матрица прямых затрат факторов | Конечный продукт | Стоимость единицы фактора |
| 1 | 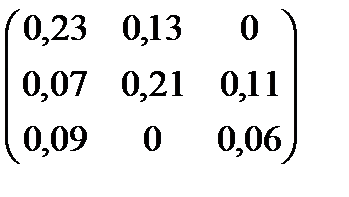
| 
| 
| 
|
| 2 | 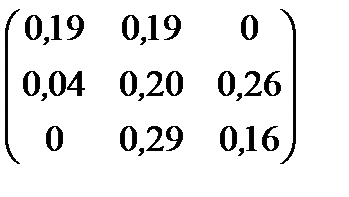
| 
| 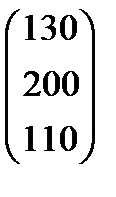
| 
|
| 3 | 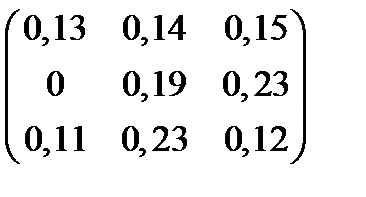
| 
| 
| 
|
| 4 | 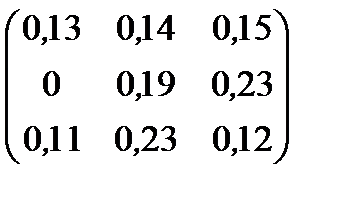
| 
| 
| 
|
| 5 | 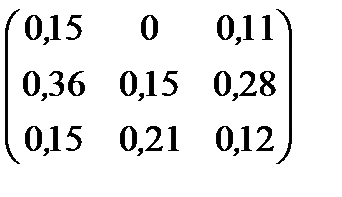
| 
| 
| 
|
| 6 | 
| 
| 
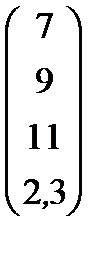
| 
|
| 7 | 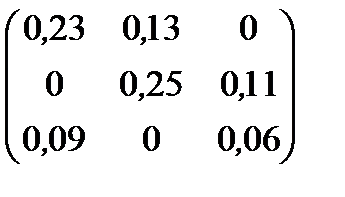
| 
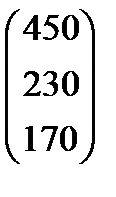
| 
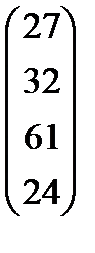
| 
|
| 8 | 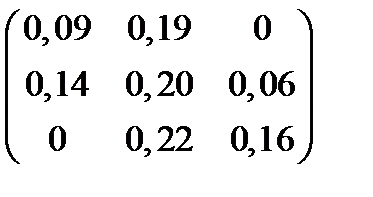
| 
| 
| 
|
| 9 | 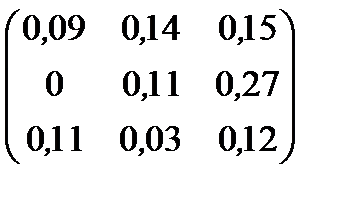
| 
| 
| 
|
| 10 | 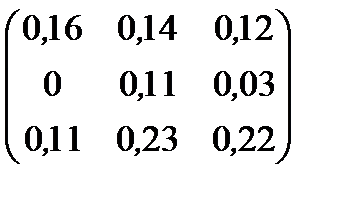
| 
| 
| 
|
| 11 | 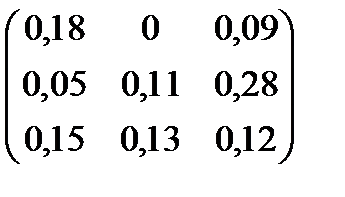
| 
| 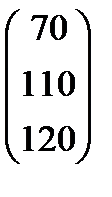
| 
|
| 12 | 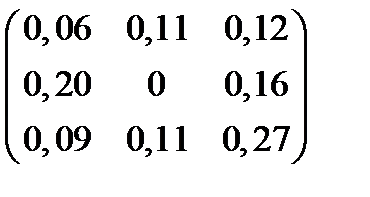
| 
| 
| 
|
| 13 | 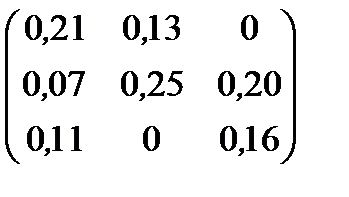
| 
| 
| 
|
| 14 | 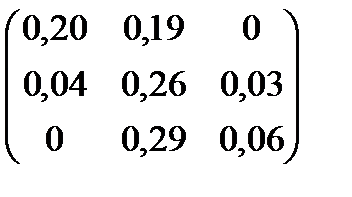
| 
| 
| 
|
| 15 | 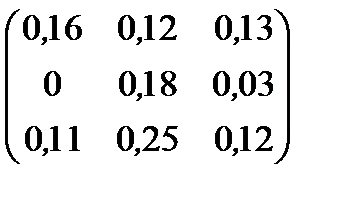
| 
| 
| 
|
| 16 | 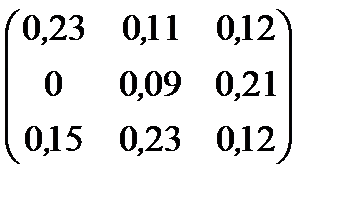
| 
| 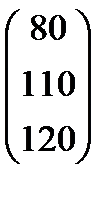
| 
|
| 17 | 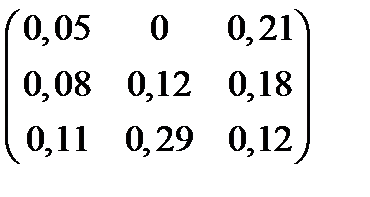
| 
| 
| 
|
| 18 | 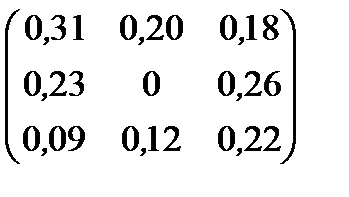
| 
| 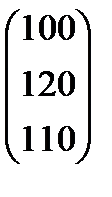
| 
|
| 19 | 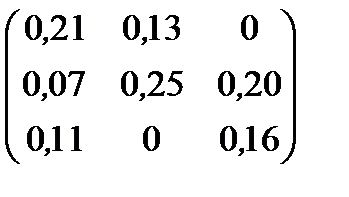
| 
| 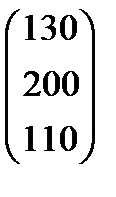
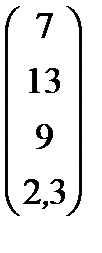
| 
|
| 20 | 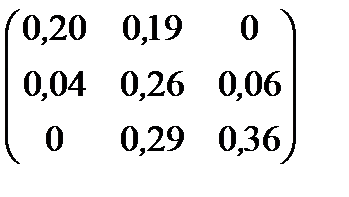
| 
| 
| 
|
| 21 | 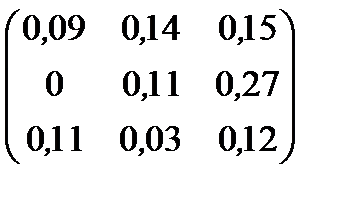
| 
| 
| 
|
Дата: 2019-03-05, просмотров: 955.