В народном хозяйстве вырабатывается большое число наименований различных видов и типов продукции.
Учесть все их при построении балансовой модели производства часто невозможно из–за отсутствия данных, а также вследствие большого объёма технической информации.
Иногда целесообразно проводить укрупнение (объединение) балансовой таблицы.
При этом возможно объединение таких видов продукции, которые являются результатом последовательной переработки тех или иных видов сырья (например, железная руда – чугун – сталь – прокат).
Такое объединение называется вертикальным.
Кроме того, возможно объединение продуктов, сходных по своему экономическому назначению, потребительским свойствам (различные виды топлива, зерна, химикатов и т.п.), именуемое горизонтальным объединением.
После объединения, например, двух объектов экономической системы 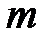 –го и
–го и 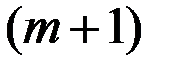 –го коэффициент прямых затрат объединённого объекта
–го коэффициент прямых затрат объединённого объекта
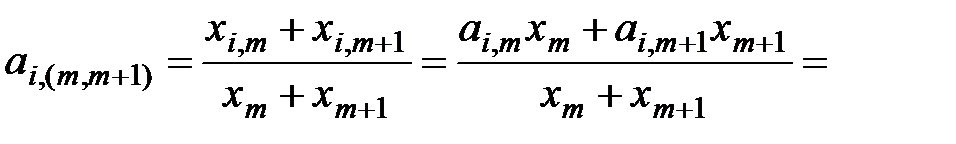
 ,
,
где удельные веса объёмов производства отдельных объектов в объёме объединённого объекта определяются соотношениями:
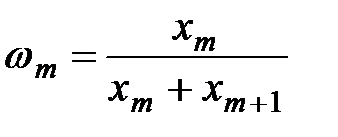 ;
;
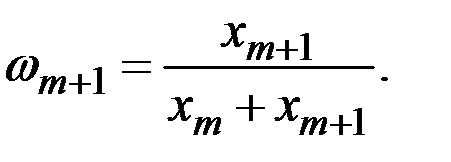
Для перехода от детальной таблицы к укрупнённой пользуются матрицей агрегирования 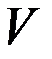 , для которой номер строки i соответствует номеру укрупнённого объекта, номер столбца j соответствует номеру исходного объекта:
, для которой номер строки i соответствует номеру укрупнённого объекта, номер столбца j соответствует номеру исходного объекта:
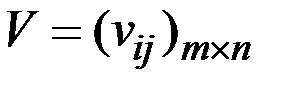 ;
;
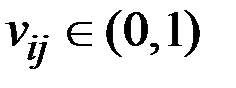 ,
, 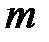 <
< 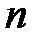 .
.
Например,
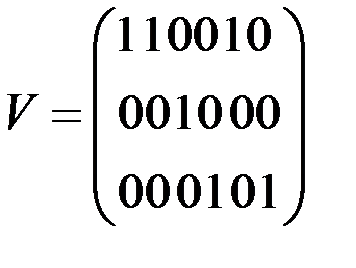 .
.
Данная матрица агрегирования соответствует случаю, когда:
1–й объединённый объект включает 1, 2 и 5–й исходные объекты;
2–й объединённый объект включает 3–й исходный объект;
3–й объединённый объекты включает 4–й и 6–й исходные объекты.
Процесс объединения в матричной форме может быть записан следующим образом:

где 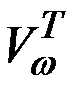 – матрица, полученная из
– матрица, полученная из 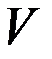 путём транспонирования и замены единичных элементов значениями удельных весов продукции отдельных объектов в соответствующем укрупнённом объекте.
путём транспонирования и замены единичных элементов значениями удельных весов продукции отдельных объектов в соответствующем укрупнённом объекте.
Тогда на основании уравнений (2.4) и (2.9) будем иметь
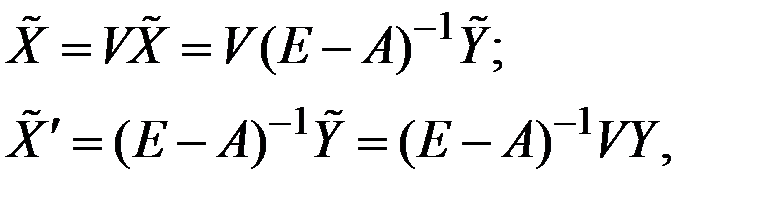
где 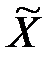 получено при укрупнении результатов расчёта по исходной балансовой таблице, а
получено при укрупнении результатов расчёта по исходной балансовой таблице, а 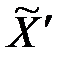 получено при расчётах по укрупнённой таблице, причём
получено при расчётах по укрупнённой таблице, причём 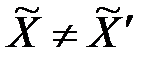 из–за потери информации.
из–за потери информации.
Возникает проблема такого укрупнения, при котором вектор 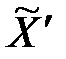 должен как можно меньше отличаться от вектора
должен как можно меньше отличаться от вектора 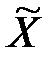 .
.
Смешанные балансовые задачи
Конкретные особенности производства и имеющиеся данные приводят к различным дополнениям и видоизменениям общей схемы построения баланса и решения балансовых уравнений.
Иногда по ряду объектов задаются объёмы производства этих объектов, а по ряду других – объёмы конечного продукта, т.е. смешанный состав неизвестных в балансовой модели производства (табл. 2.3).
Таблица 2.3
Блочно–матричный вид смешанной балансовой модели производства
| Валовый выпуск | Структурная матрица | Конечный продукт |
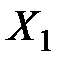
| 
| 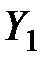
|
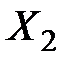
| 
| 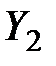
|
Все виды продукции делятся на две группы (по строкам).
В первой группе искомыми являются валовые выпуски 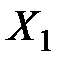 , заданы объёмы конечного продукта
, заданы объёмы конечного продукта 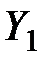 .
.
Во второй группе искомыми являются 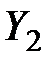 и заданными
и заданными 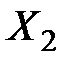 .
.
Запишем в блочно–матричном виде системы балансовых уравнений:
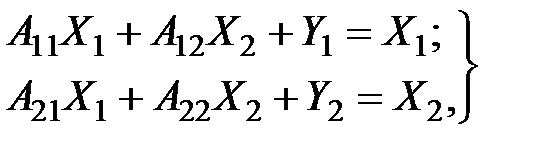 (2.10)
(2.10)
где 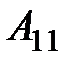 – матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты (группа 1);
– матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты (группа 1);
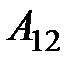 – матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты, на производство продукции объектов, по которым заданы объёмы производства;
– матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты, на производство продукции объектов, по которым заданы объёмы производства;
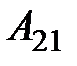 – матрица коэффициентов прямых затрат объектов, по которым заданы валовые объёмы производства, на производство продукции объектов, по которым заданы конечные продукты;
– матрица коэффициентов прямых затрат объектов, по которым заданы валовые объёмы производства, на производство продукции объектов, по которым заданы конечные продукты;
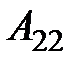 – матрица коэффициентов прямых затрат объектов, по которым заданы валовые объёмы производства.
– матрица коэффициентов прямых затрат объектов, по которым заданы валовые объёмы производства.
Решение системы (2.10) проводится в два этапа.
Сначала решается первое уравнение и находится вектор 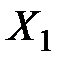 :
:
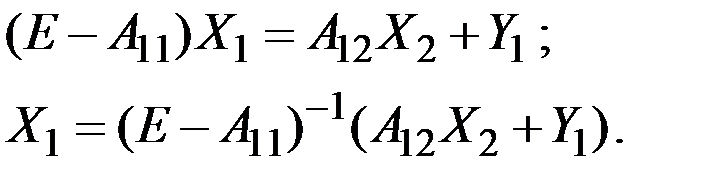
Затем найденный вектор 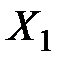 подставляется во второе уравнение и определяется вектор
подставляется во второе уравнение и определяется вектор 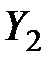 :
: 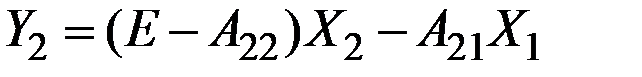 .
.
Дата: 2019-03-05, просмотров: 478.