Экономических систем
Для функционирования отдельных экономических объектов необходимы не только продукция других экономических объектов этой системы, но и такие факторы производства, как производственные фонды (оборудование, производственные площади и т.д.), природные ресурсы (вода, газ, лес, полезные ископаемые и т.д.), труд.
Кроме этого, экономическая система может получать продукцию от других экономических систем.
Ограниченность факторов производства и поставок из других экономических систем является причиной того, что реально не всякий вектор конечной продукции может быть произведён данной экономической системой.
Поэтому при планировании необходимо не только определять потоки продукции между отдельными объектами системы, но и найти потребность системы в факторах производства и поставок извне.
При этом допустимым для экономической системы является такой план, при котором потребности в факторах производства и импорте не превышают соответствующих ограничений.
Рассмотрим способ определения потребности системы в факторах производства и поставок извне.
При этом как факторы производства, так и импортируемые продукты будем называть факторами.
Пусть имеем 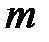 факторов.
факторов.
Потребность системы в факторах на планируемый период будем обозначать вектором
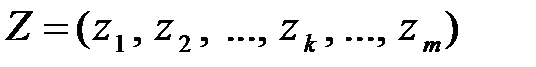 ,
,
где 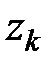 – потребность в
– потребность в 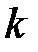 –м факторе.
–м факторе.
Потребность всех объектов в факторах может быть охарактеризована матрицей коэффициентов прямых затрат факторов:
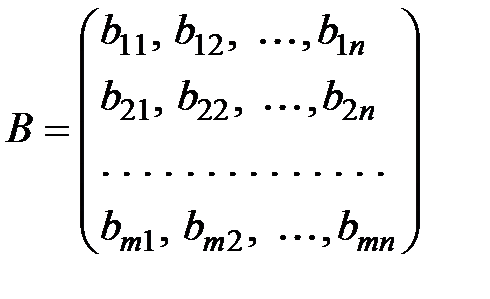 .
.
Числа 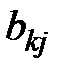 – коэффициенты прямых затрат факторов.
– коэффициенты прямых затрат факторов.
Коэффициент 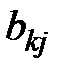 указывает, какое количество
указывает, какое количество 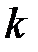 –го фактора необходимо j–му объекту для того, чтобы этот объект мог произвести одну единицу продукции
–го фактора необходимо j–му объекту для того, чтобы этот объект мог произвести одну единицу продукции 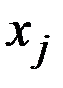 .
.
Если вектор полного выпуска продукции объектами системы есть 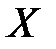 , то суммарная потребность системы в
, то суммарная потребность системы в 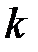 –м факторе
–м факторе
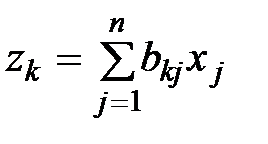 ,
, 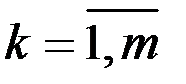
или в матричной форме
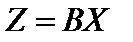 . (2.7)
. (2.7)
Вектор 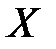 является решением системы балансовых уравнений, поэтому с учётом формы (2.5) из выражения (2.7) получим
является решением системы балансовых уравнений, поэтому с учётом формы (2.5) из выражения (2.7) получим
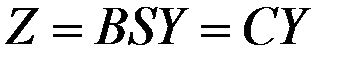 . (2.8)
. (2.8)
Соотношение (2.8) позволяет определить суммарную потребность Z в факторах для любого вектора конечной потребности 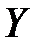 , а также установить экономический смысл матрицы
, а также установить экономический смысл матрицы 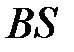 .
.
Для этого рассмотрим частный вид вектора 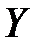 , когда
, когда 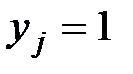 , а
, а 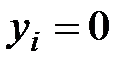 при
при 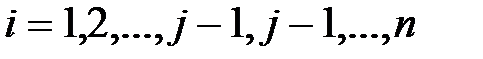 .
.
Тогда на основании соотношения (2.8) будем иметь
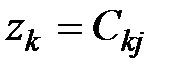

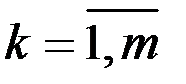 ,
,
где 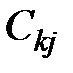 (
( 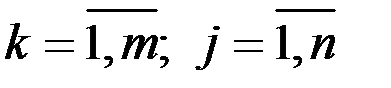 ) – элементы матрицы
) – элементы матрицы 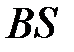 .
.
Таким образом, элемент 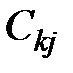 показывает, какое суммарное количество
показывает, какое суммарное количество 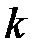 –го фактора необходимо системе для того, чтобы
–го фактора необходимо системе для того, чтобы 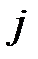 –й объект мог выпустить одну единицу конечной продукции
–й объект мог выпустить одну единицу конечной продукции 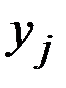 .
.
В связи с этим матрицу 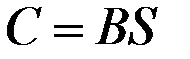 называют матрицей коэффициентов полных затрат факторов.
называют матрицей коэффициентов полных затрат факторов.
Количество каждого фактора, которое может быть использовано системой, ограничено.
Это значит, что известны 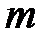 чисел
чисел 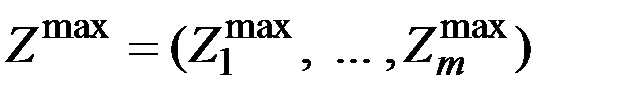 , имеющих следующий смысл: план для данной экономической системы допустим, если требуется для его реализации количество
, имеющих следующий смысл: план для данной экономической системы допустим, если требуется для его реализации количество 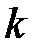 –го фактора не большее
–го фактора не большее 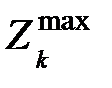 для всех
для всех 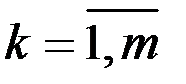 .
.
Поэтому экономическая система может выпустить только такой вектор конечной продукции 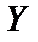 , который удовлетворяет условию
, который удовлетворяет условию
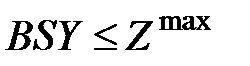 .
.
Пример 2.1. Рассмотрим экономическую систему, состоящую из двух объектов. За предшествующий период исполнение баланса характеризуется данными, представленными в первых 5 столбцах табл. 2.2. При этом в системе использованы следующие факторы: 1) труд (в человеко–часах) и 2) капиталовложения (в тысячах рублей). Требуется составить матрицы прямых и полных затрат экономической системы. Найти показатели нового плана: валовую продукцию и суммарную потребность системы в факторах при заданном объёме конечной продукции (табл. 2.2).
Таблица 2.2
Исполнение баланса производства
| Номер объекта | Потребление | Валовый | Конечная | ||
| и фактора | 1 | 2 | выпуск | продукция | |
| Производство | 1 2 | 100 275 | 160 40 | 500 400 | 480 100 |
| Факторы: Труд Кап.вложения | 1 2 | 250 750 | 80 800 | – – | – – |
Решение. Используя формулу определения коэффициентов прямых затрат (технологических коэффициентов) 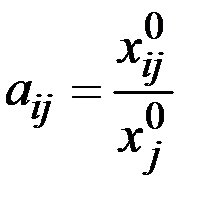
вычисляем эти коэффициенты
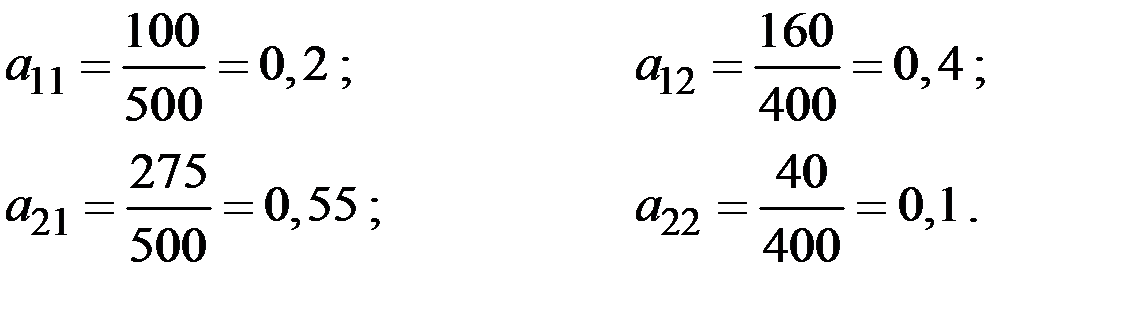
Аналогично определяем коэффициенты прямых затрат факторов, исходя из того, что коэффициент 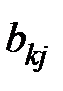 прямых затрат
прямых затрат 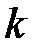 –го фактора для
–го фактора для 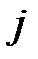 –го объекта равен отношению затрат этого фактора объектом к полному выпуску продукции этим объектом, взятым за прошедший период:
–го объекта равен отношению затрат этого фактора объектом к полному выпуску продукции этим объектом, взятым за прошедший период:
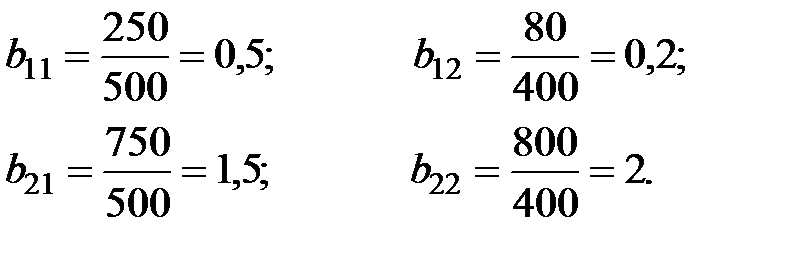
Таким образом, имеем матрицы коэффициенты прямых затрат производства и факторов
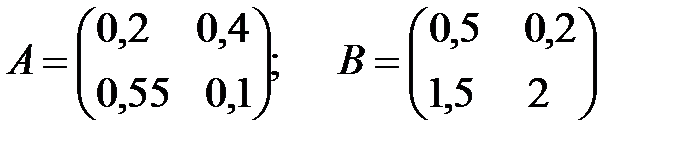 .
.
Далее вычисляем матрицу полных затрат производства  .
.
Так как
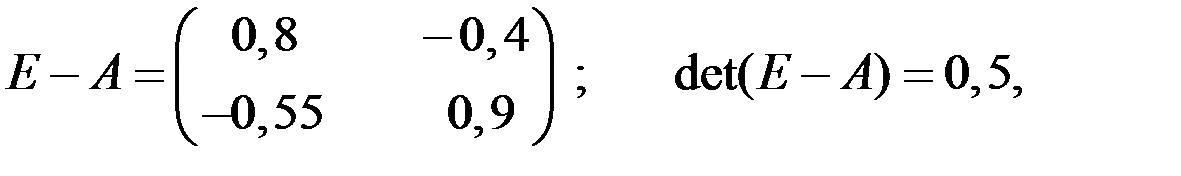
то
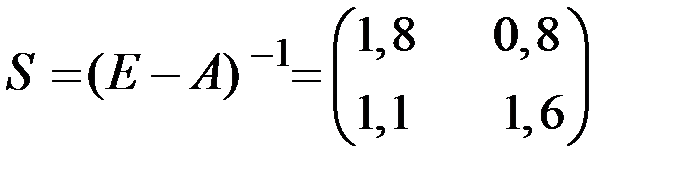 .
.
Вычислим матрицу коэффициентов полных затрат факторов:
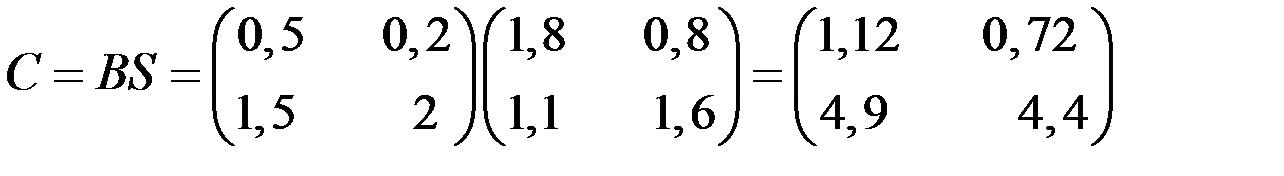 .
.
Зная значение вектора конечной продукции 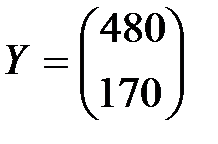 , по формулам (2.5) и (2.8) можем найти показатели плана: валовую продукцию и суммарную потребность системы в факторах.
, по формулам (2.5) и (2.8) можем найти показатели плана: валовую продукцию и суммарную потребность системы в факторах.
Тогда валовая продукция объектов составит величины
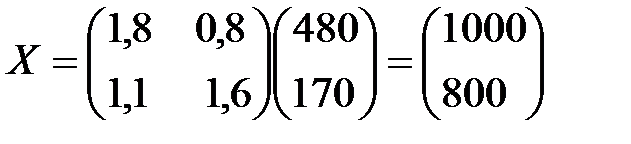 .
.
Потребность системы в факторах составит величины
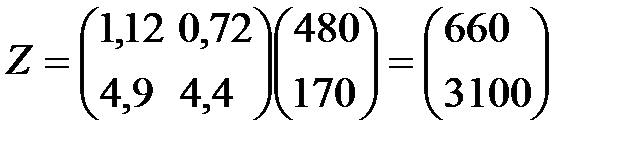 .
.
Отсюда заключаем, что запланированный выпуск конечного продукта может быть достигнут при валовом выпуске объектов 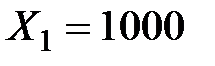 и
и 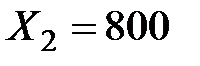 при суммарных затратах труда
при суммарных затратах труда 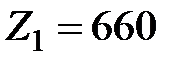 и при затратах капиталовложений
и при затратах капиталовложений 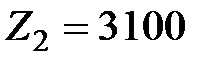 .
.
Дата: 2019-03-05, просмотров: 465.