Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.
В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции
f(x1, x2, …, х n)
при условиях
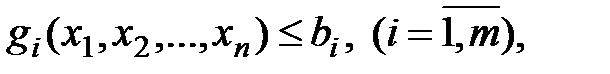
где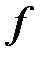 
и 
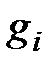– заданные функции,
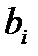– некоторые действительные числа.
В зависимости от свойств функци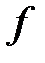й 
и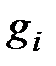 
математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определённых классов задач.
Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования.
При этом если все функци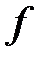и 
и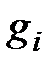 
линейные, то соответствующая задача является задачей линейного программирования.
Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.
Наиболее изученным разделом математического программирования является линейное программирование.
Для решения задач линейного программирования разработан целый ряд эффективных методов (например, симплексный метод), алгоритмов и программ.
Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования.
Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования.
В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что её переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно–линейного программирования.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
В задачах параметрического программирования целевая функция или функции, определяющие область возможных изменений переменных, либо то и другое зависят от некоторых параметров.
В задачах дробно–линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными.
Выделяют отдельные классы задач стохастического и динамического программирования.
Если в целевой функции или в функциях, определяющих область возможных изменений переменных, содержатся случайные величины, то такая задача относится к задаче стохастического программирования.
Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
Производственные функции
Производственная функция – функция, устанавливающая количественную связь между результатом (эффектом) некоторого процесса и условиями его получения, по крайней мере часть из которых является управляемыми (хотя и не обязательно) в рамках изучаемого процесса.
Под результатом чаще всего понимается выпуск продукции (фактический или максимально возможный) некоторой производственной единицы – предприятия, отрасли, региона, народного хозяйства в целом в натуральном или денежном выражении, а под условиями – ресурсы (затраченные, использованные или наличные).
В рамках производственной функции ресурсы обычно называют факторами производства.
Для отдельного предприятия или отрасли, выпускающей однородный продукт, производственные функции часто связывают объём выпуска в натуральных единицах с затратами рабочего времени по видам трудовой деятельности, различным видам сырья, энергии и т.д. (измеренными, как и выпуск, в натуральных единицах). Они отражают реально действующую технологию или спектр возможных технологий.
Производственные функции на уровне крупных отраслей, регионов или народного хозяйства в целом обычно используют агрегированные стоимостные измерители и отражают не только (и не столько) технологические, но и экономические закономерности («Затраты – Выпуск»).
Концепция производственных функций базируется в первую очередь на идее замещения между факторами, т.е. на гипотезе о том, что один и тот же выпуск может быть получен при разных комбинациях используемых ресурсов.
При этом речь идёт о замещении как между различными ресурсами в рамках одной и той же технологии, так и между различными технологиями производства одного и того же продукта или между различными продуктами, имеющими разную ресурсоёмкость.
Формально производственная функция записывается в виде:
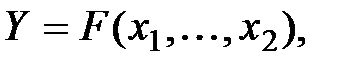
где Y – объём выпуска,
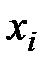– объём i –го фактора производства.
Вид функции F и значения её параметров определяются из теоретических представлений и имеющейся конкретной информации о моделируемом объекте.
Оценка параметров производится методами регрессионного анализа, поэтому любая оценённая производственная функция представляет собой уравнение регрессии.
Производственные функции народнохозяйственного уровня чаще всего имеют вид:
Y = F(K, L) или Y = F(K, L, t),
где K и L характеризуют ресурсы (затраты) основных фондов (капитала) и живого труда (численность работников),
t – время, вводимое для описания воздействия прочих факторов (неучтённых в K и L), среди которых главную роль играет научно–технический прогресс.
Наиболее часто используются производственная функция Кобба–Дугласа, производственная функция с постоянной эластичностью замещения (CES –функция), а также производственная функция леонтьевского типа и линейная производственная функция.
В теоретических работах в некоторых случаях используются производственные функции, записанные в неявном виде, иногда многофакторные.Производственные функции позволяют рассчитать ряд характеристик, описывающих различные стороны производственного процесса.
Наиболее часто используются следующие характеристики.
1. Предельная производительность (предельный продукт) i –го фактора:
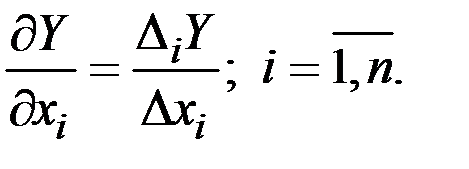
Показывает, на сколько единиц увеличится выпуск при увеличении затрат i–го фактора на одну (малую) единицу и при неизменном количестве остальных факторов.
Обычно предельная производительность меньше средней:
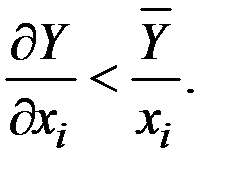
2. Частная эластичность выпуска по i–му фактору (частная факторная эластичность):
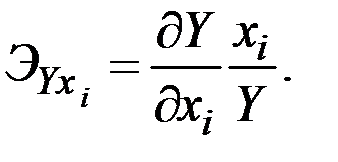
Показывает, на сколько процентов увеличится выпуск при увеличении затрат i–го фактора на 1% при неизменном количестве остальных факторов. Представляет собой отношение предельной и средней производительностей.
3. Предельная норма замены (замещения) i–го фактора j –м.
Показывает количество j –го фактора, которое требуется для замены одной единицы i–го фактора при сохранении неизменного объёма выпуска и неизменного количества остальных факторов.
По определению предельная норма замены равна:
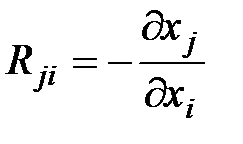при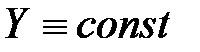 
, 
.
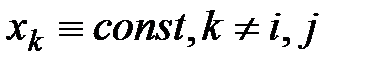Легко видеть, что предельная норма замены равна отношению предельной производительности i–го фактора к предельной производительности j–го фактора со знаком минус:
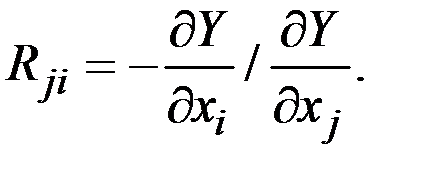
4. Эластичность замены (замещения) i–го фактора j–м. Наряду с предельной нормой замены характеризует возможности замещения одного фактора другим. В простейшем случае определяется как
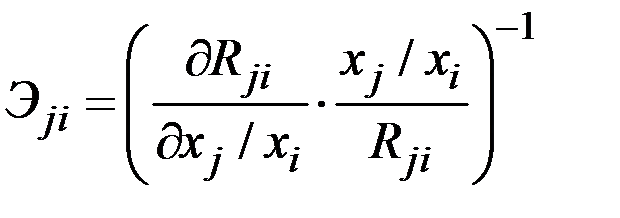при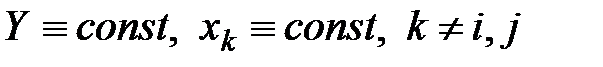 
.
Имеются и другие определения эластичности замещения для многофакторных производственных функций.
Все существующие определения эквивалентны только для двухфакторных линейно однородных производственных функций.
В этом случае все они приводят к формуле
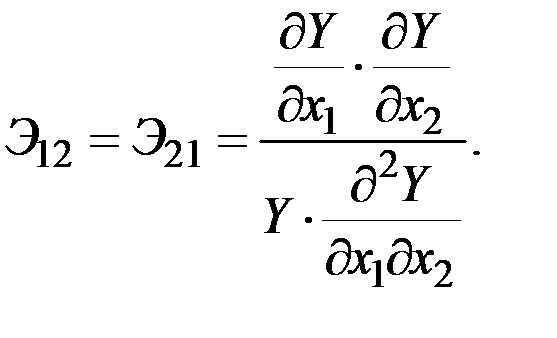
1. Производственная функция Кобба–Дугласа – наиболее часто используемая производственная функция, которая имеет следующий вид
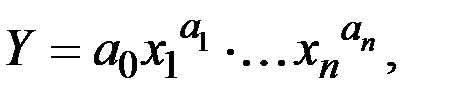
где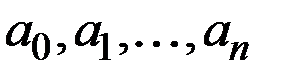 
– параметры функции.
Частная эластичность выпуска по каждому ресурсу в рамках производственной функции Кобба–Дугласа постоянна и равна соответствующему показателю степени. Эластичность замены между любыми двумя ресурсами равна единице.
Предельная производительность i–го ресурса имеет вид: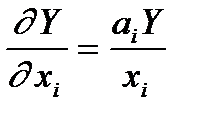 
.
Предельные нормы замещения равны:
.
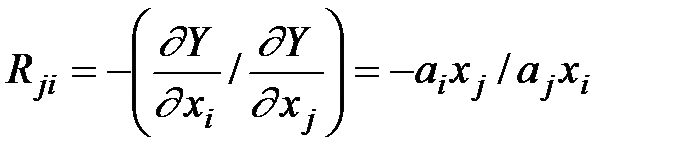При пропорциональном росте объёмов производственных ресурсов предельная норма замещения не изменяется.
Удовлетворяя большинству теоретических требований, эта функция сочетает в себе простую математическую запись и небольшое количество параметров, численные значения которых могут быть легко оценены.
В частности, после логарифмического преобразования функции Кобба–Дугласа её параметры могут быть оценены методом наименьших квадратов.
Кроме того, эта функция может быть приведена к виду:
,
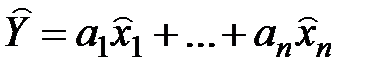где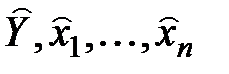 
– темпы прироста.
В непрерывном времени это равенство является точным, в дискретном – приближенным.
В случаях, когда требуется отразить воздействие научно–технического прогресса на экономические процессы, часто используется производственная функция Кобба–Дугласа–Тинбергена, имеющая вид:
где t – время, g – темп прироста выпуска под влиянием НТП.
2. Производственная функция леонтьевского типа – производственная функция, в рамках которой отсутствует возможность замещения между ресурсами. Имеет вид
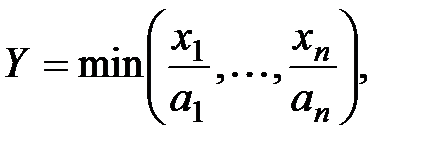
где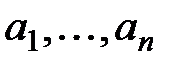 
– параметры.
Предельная норма замены между любыми двумя ресурсами для указанной функции равна бесконечности, а эластичность замещения – нулю.
Таким образом, в рамках леонтьевской функции предполагается, что ресурсоёмкость производства по каждому ресурсу фиксирована и, следовательно, объём выпуска однозначно определяется количеством лимитирующего фактора.
Обобщённая производственная функция леонтьевского типа имеет вид
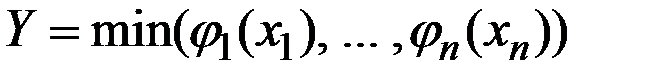
и обладает практически теми же свойствами, что и отмеченная выше.
3. Линейная производственная функция – наиболее простая из производственных функций. Имеет вид:
,
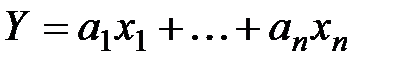где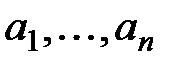 
– параметры.
Линейная производственная функция предполагает неограниченные возможности замещения между ресурсами (все предельные нормы замены постоянны, а эластичности равны бесконечности). Является предельным случаем производственной функцией с постоянной эластичностью замещения, когда все эластичности стремятся к бесконечности. Используется редко, поскольку гипотеза о линейности в большинстве случаев не является адекватной.
4. Производственную функцию с постоянной эластичностью замещения часто называют функцией CES (от англ. constant elastisity of substitution).
В двухфакторном случае имеет вид:
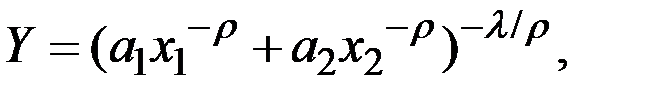
где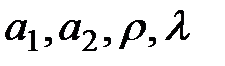 
– параметры.
Эластичность замещения в рамках этой функции равна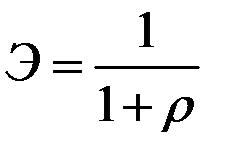 
.
Предельная производительность i–го ресурса
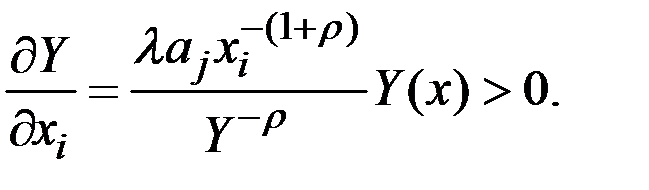
Эластичность выпуска по i–му ресурсу
,
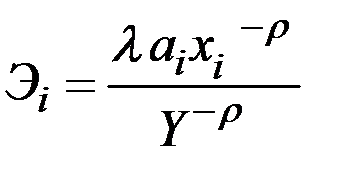а предельные нормы замещения равны
.
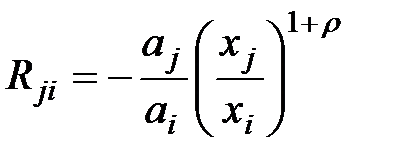Функция CES считается наиболее гибкой и теоретически содержательной. Линейная производственная функция и функция Кобба–Дугласа являются её предельными случаями:
первая – при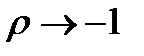 
(т.е. при 
),
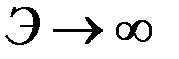вторая – при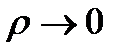 
(т.е. при 
).
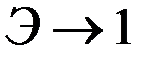Однако статистическая оценка параметров функции затруднена.
Для отражения воздействия научно–технического прогресса используется следующая модификация функции CES:
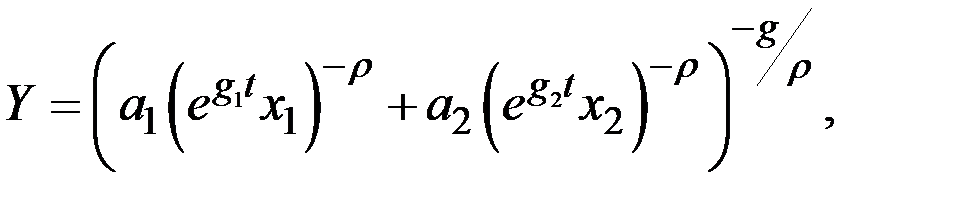
где t – время, g – темп прироста выпуска под влиянием НТП.
В соответствии с различными определениями эластичности замещения существуют различные обобщённые функции на случай n ресурсов.
Наиболее известны среди них функции
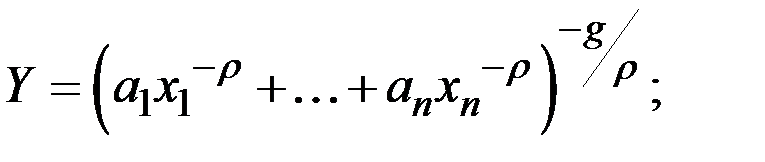
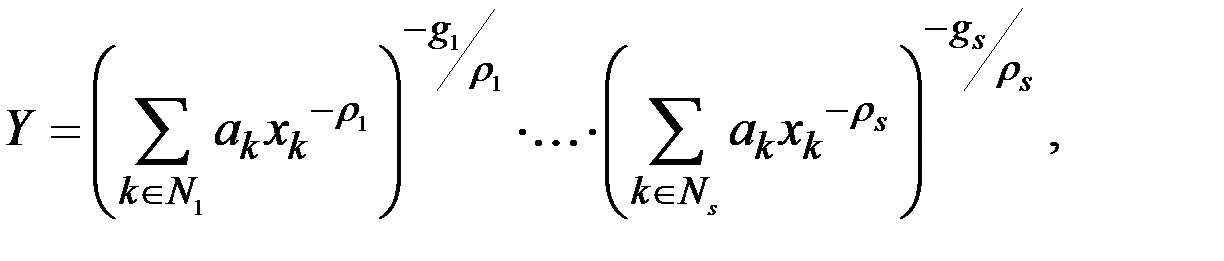
где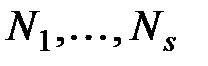 
– непересекающиеся подмножества индексов, в сумме составляющие множество 
.
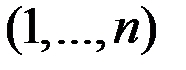Для первой функции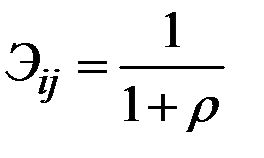 
при всех i, j а для второй:
Отметим некоторые предположения, используемые при применении производственных функций.
1. Производство невозможно при отсутствии хотя бы одного ресурса, т.е.
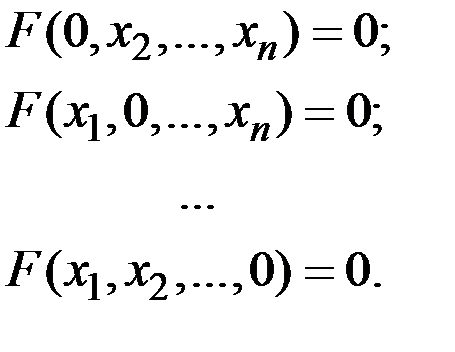
Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Полное его отсутствие не может быть компенсировано другими ресурсами.
2. При увеличении затрат производства выпуск продукции не уменьшается:
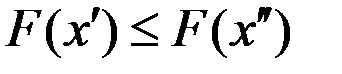при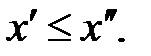 
Если F(x) дифференцируема, то последнее условие можно записать в виде:
, 
.
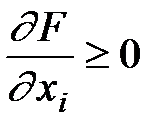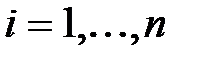3. По мере увеличения количества одного ресурса при постоянных количествах других предельная производительность использования этого ресурса не возрастает.
Для дважды дифференцируемых производственных функций можно записать:
.
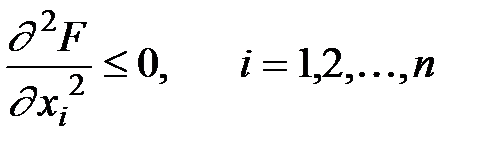Это условие означает, что рост вооружённости средствами производства приводит к росту выпуска продукции, но темп роста выпуска продукции всё время падает.
В случае экстенсивного роста производства, т.е. роста только за счёт количества ресурсов без повышения эффективности их использования, последнее соотношение имеет разумную интерпретацию: поскольку каждая следующая количественно возрастающая единица производственного ресурса должна соединяться со всё меньшим приходящимся на неё количеством других ресурсов, эффективность использования этого ресурса уменьшается.
Часто вместо третьего условия формулируется более сильное требование: F(x) – вогнутая (выпуклая вверх) функция, т.е. для любых двух неотрицательных векторов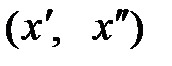 
и любого числа 
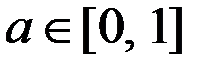справедливо неравенство
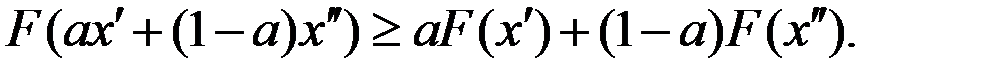
Если F(x) дважды непрерывно дифференцируема, условие вогнутости эквивалентно требованию неположительной определённости матрицы вторых производных функции F(x) при всех положительных значениях вектора ресурсов x, т.е. для всех векторов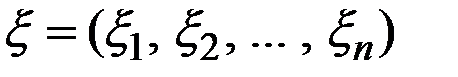 
выполняется неравенство
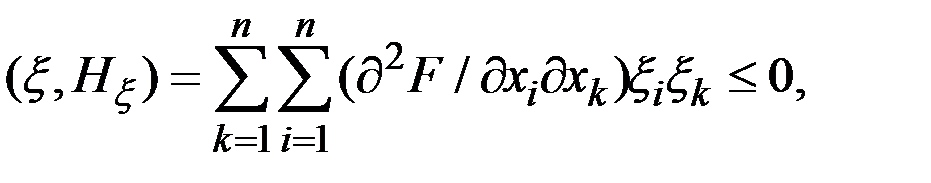
где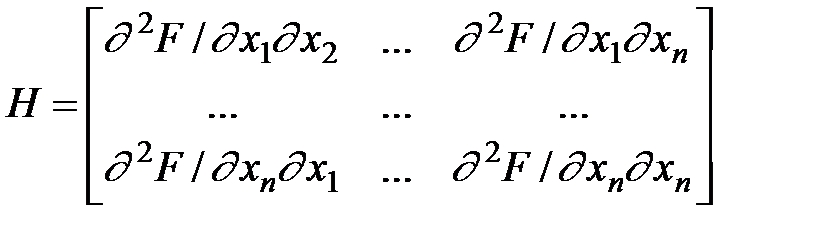 
.
Матрица H называется матрицей Гессе (или гессианом).
4. Производственная функция характеризуется определённой отдачей от расширения масштабов производства с точки зрения изменения выпуска продукции при пропорциональном изменении затрат ресурсов, которое математически выражается в умножении всех компонент вектора x на положительный скаляр t.
Принято говорить, что скалярная функция F(x) является однородной функцией степени d, если для любого вектора x и любого скаляра t она удовлетворяет соотношению
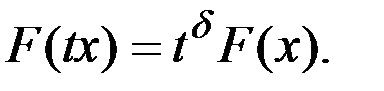
Математически данное предположение состоит в требовании однородности производственной функции.
Если d > 1, то говорят, что производственная функция характеризуется возрастающей отдачей от расширения масштабов производства.
Если d = 1 – постоянной отдачей (наиболее часто встречающийся случай), а при d < 1 – убывающей отдачей.
Спецификация ПФ – выделение факторов и выбор формы функции.
Параметризация ПФ – расчёт параметров функции по статистическим данным.
Верификация ПФ – проверка адекватности (истиности) функции.
Изокванта – множество точек , в которых производственная функция постоянна и равна заданной величине (рис. 1.1 – 1.2).
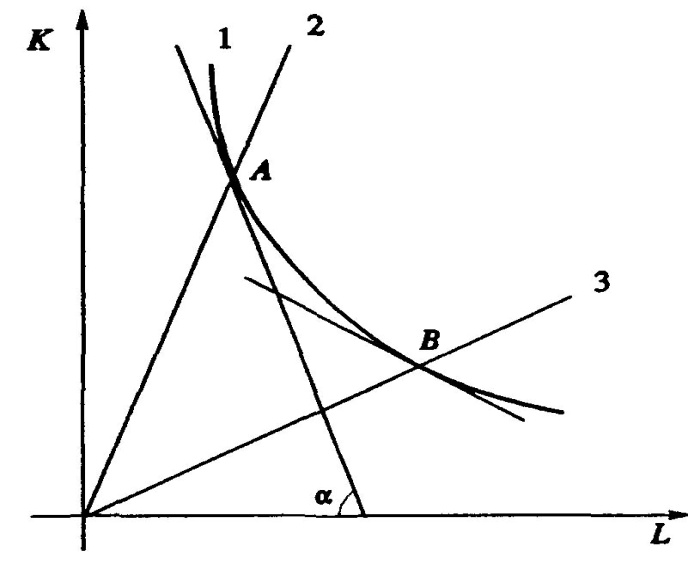
Рис. 1.1. Графическая интерпретация предельной нормы замены по изокванте
При перемещении по изокванте из точки А в точку В наклон касательной меняется. Меняется и соотношение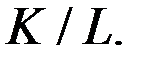 
Это соотношение постоянно вдоль каждой прямой, проходящей через начало координат (прямые 2, 3).
Величина (1/Э) показывает относительное изменение тангенса угла наклона уровня изокванты на единицу изменения соотношения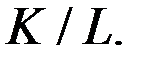
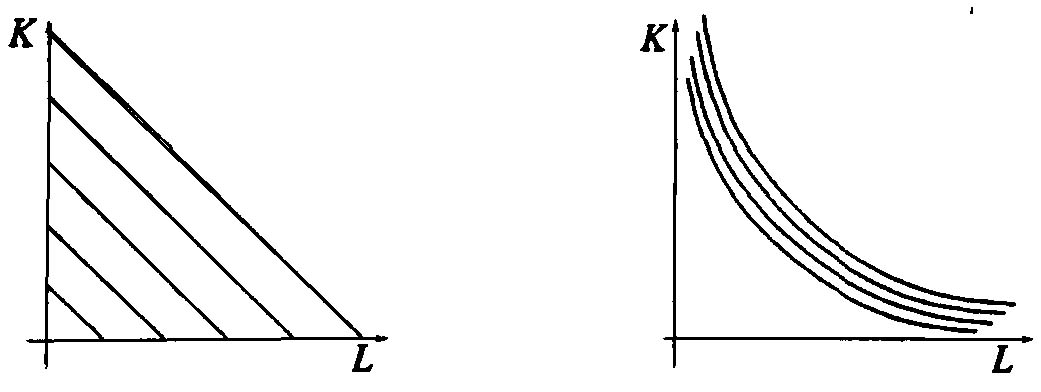
Линейная ПФ ПФ Кобба-Дугласа
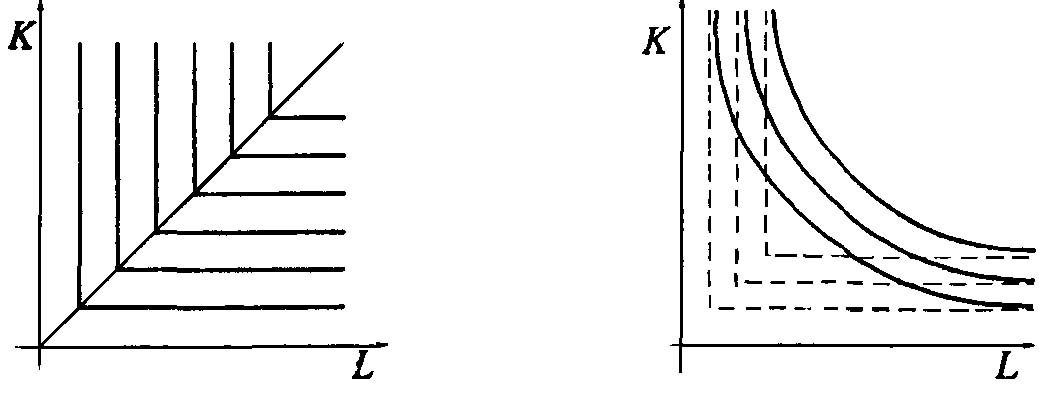
ПФ Леонтьева ПФ CES
Рис. 1.2. Семейства линий уровня различных производственных функций
Имитационное моделирование
Имитационное моделирование на ЭВМ предполагает экспериментирование по специально разработанной программе (рис. 1.3).
Основной принцип метода статистического (имитационного) моделирования состоит в построении вероятностного процесса, характеристики которого представляют решение поставленной задачи.
| Имитаторы случайных воздействий |
| Реализованная на ЭВМ модель системы |
| Статистическая обработка результатов многократного моделирования |
Рис. 1.3. Составные части статистического моделирования на ЭВМ
Моделирующий алгоритм приближённо воспроизводит процесс–оригинал в смысле его функционирования во времени, причём имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания.
После построения вероятностной модели решаемой задачи, она многократно имитируется на ЭВМ и, после проведения достаточно большого числа испытаний и накопления необходимого объёма выборочных данных, находится оценка требуемых параметров.
При имитационном моделировании динамические процессы системы–оригинала подменяются процессами, имитируемыми моделирующим алгоритмом в абстрактной модели.
Но при этом соблюдаются такие же соотношения длительностей, логических и временных последовательностей, как и в реальной системе.
Предпосылками имитационного моделирования процессов и систем является следующее.
1. Часто исследование только по реальным статистическим данным не даёт необходимой полноты исследования, требует большого объёма исходной информации, которую не всегда удаётся получить, либо её получение связано со значительными затратами.
Иногда и достоверность реальной статистики не удовлетворяет требованиям исследования.
В этом случае недостающая информация может быть сгенерирована с применением ЭВМ методом Монте–Карло (методом статистического моделирования) по заранее заданным вероятностным характеристикам процесса.
2. Другой предпосылкой целесообразности применения статистического моделирования является трудность аналитического описания взаимодействий элементов системы и учёта случайных факторов, в условиях действия которых функционирует рассматриваемая система.
3. Моделирование позволяет исследовать поведение системы в условиях, трудно наблюдаемых в действительности.
4. Моделирование позволяет интенсифицировать исследование.
Преимущества имитационных моделей не умаляют значения моделей аналитических. Их надо считать взаимодополняющими инструментами экономико–математического анализа.
Во–первых, имитационная модель может включать в себя в качестве оптимизационных блоков те элементы исследуемой системы, которые могут быть формализованы в виде соответствующих оптимизационных аналитических моделей.
Во–вторых, построение имитационных моделей в ряде случаев предшествует построению оптимизационных аналитических моделей, поскольку прежде чем оптимизировать функционирование той или иной системы, необходимо понять особенности этого функционирования.
В этих случаях предварительные исследования на имитационных моделях часто дают возможность построения достаточно простых и эффективных аналитических моделей.
К недостаткам имитационного моделирования можно отнести:
1) отсутствие структурированных принципов построения имитационных моделей (что требует значительной проработки каждого конкретного случая её построения);
2) методологические трудности поиска оптимальных решений;
3) трудности, связанные со сбором и подготовкой репрезентативных статистических данных;
4) уникальность имитационных моделей, что затрудняет использование готовых программных продуктов;
5) сложность анализа и осмысления результатов, полученных в результате вычислительного эксперимента;
6) достаточно большие затраты времени и средств, особенно при поиске оптимальных траекторий поведения исследуемой системы.
Одним из основных параметров при имитационном моделировании является модельное время, которое отображает реальное время функционирования исследуемой системы.
В зависимости от способа продвижения модельного времени методы моделирования подразделяются:
1) на методы с приращением временного интервала;
2) методы с продвижением времени до особых состояний.
В первом случае модельное время продвигается на некоторую величину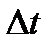 
. Далее определяются изменения состояния элементов системы, которые произошли за это время. После этого модельное время снова продвигается на величину 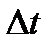и т.д. до конца периода моделирования. Шаг приращения выбирается, как правило, постоянным, но в общем случае он может быть и переменным. Этот метод носит название «принцип ».
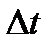Во втором случае в текущий момент модельного времени t сначала анализируются будущие особые состояния системы (иногда их называют события), которые изменяют динамику функционирования исследуемой системы.
В общем случае в качестве особых состояний можно выделить (на примере моделирования систем массового обслуживания): поступление заявок на обслуживание; начало обслуживания заявки; освобождение канала после обслуживания заявки; завершение моделирования.
В самом общем случае в системе могут быть выделены события и других типов, например, возникновение отказа (поломки) канала обслуживания в процессе обслуживания заявки, а также завершение восстановления устройства после отказа.
После анализа событий выбирается наиболее раннее время (момент) и модельное время продвигается до момента наступления этого события.
При этом считается, что состояние системы не изменяется между двумя соседними событиями.
Затем определяется реакция системы на выбранное событие, в частности определяется характер и момент наступления нового особого состояния (события), и т.д.
Процедура повторяется до завершения периода моделирования.
Данный принцип называют «принципом особых состояний».
Модель в этом случае работает, «перепрыгивая» от одного события к другому, значительно экономя машинное время моделирования.
Поскольку имитационный эксперимент выполняется на ЭВМ, как правило, с очень высоким быстродействием, время работы модели весьма незначительно (минуты).
Такое отражение в ЭВМ реального процесса называют «сжатием времени», преимущества которого становятся очевидными, если попытаться получить эту же информацию, используя реальную моделируемую систему.
Время окончания работы моделируемого алгоритма либо задаётся, как правило, с помощью ограничения, накладываемого непосредственно на продолжительность имитируемого периода, на так называемую глубину моделирования, либо выход из алгоритма осуществляется по достижении требуемой точности статистических оценок рассчитываемых характеристик моделируемой системы.
Степень детализации элементов моделируемой системы в условиях многократной реализации модели требует своего оптимального решения: с одной стороны, желательно до минимума сократить объём вычислений, с другой – не потерять при этом требуемой точности расчётов.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 1
1. В чём суть и преимущества моделирования как метода исследования и познания?
2. Что такое математическая модель?
3. В чём отличие статических моделей от динамических, детерминированных моделей от стохастических?
4. Назовите этапы построения экономико–математической модели. Приведите пример построения и уточнения модели.
5. В чём проявляется системный подход к разработке и исследованию экономико–математических моделей?
6. Приведите классификацию и охарактеризуйте основные типы математических моделей.
7. Охарактеризуйте основные процессы специального типа, используемые в предпосылках моделей экономики.
8. Что такое производственная функция?
9. Охарактеризуйте основные виды и особенности производственных функций.
10. Каковы особенности имитационного моделирования?
БАЛАНСОВЫЕ МОДЕЛИ ЭКОНОМИКИ
Дата: 2019-03-05, просмотров: 409.
