При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение результативного признака в текущий момент времени 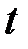 формируется под воздействием ряда факторов, действовавших в прошлые моменты времени .

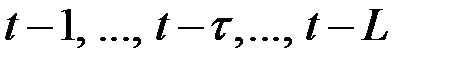Например, на выручку от реализации (прибыль компании) текущего периода могут оказывать влияние расходы на рекламу или проведение маркетинговых исследований, сделанные компанией в предшествующие моменты времени.

Величина 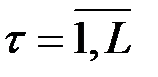 характеризует запаздывание в воздействии фактора на результат и называется в эконометрике лагом, а временные ряды самих факторных экзогенных переменных, сдвинутые на один или более моментов времени, – лаговыми переменными.

Часто требуется решение задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей.

Например, как повлияют инвестиции в промышленность на валовую добавленную стоимость этой отрасли экономики будущих периодов или как может измениться объём ВВП, произведённого в периоде 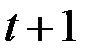, под воздействием увеличения денежной массы в периоде ?

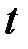Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных.

Эти модели называются моделями с распределённым лагом.

Модель с распределённым лагом порядка 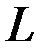 имеет вид

.

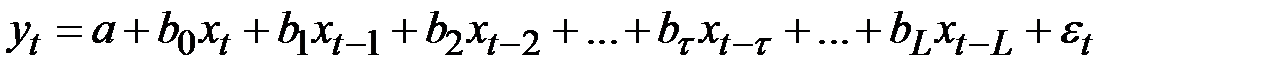Модель говорит о том, что если в некоторый момент времени 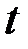 происходит изменение переменной 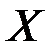, то это изменение будет влиять на значения переменной  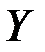в течение  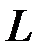следующих моментов времени.

Коэффициент регрессии 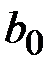 при переменной  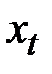характеризует среднее абсолютное изменение  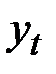при изменении  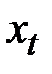на одну единицу своего измерения в некоторый фиксированный момент времени  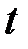без учёта воздействия лаговых значений фактора Х.

Этот коэффициент называют краткосрочным мультипликатором.

В момент 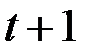 совокупное воздействие факторной переменной  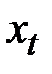на результат  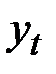составит  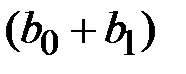условных единиц, в момент  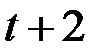это воздействие можно охарактеризовать суммой  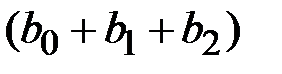и т.д.

Полученные таким образом суммы называют промежуточными мультипликаторами.

С учётом конечной величины лага можно сказать, что изменение переменной 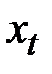 в момент  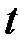на 1 условную единицу приведёт к общему изменению результата через  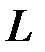моментов времени на  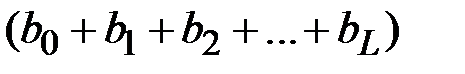абсолютных единиц.

Введём следующее обозначение:

.

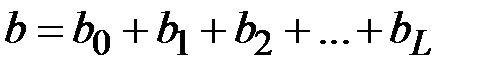Величину 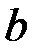 называют долгосрочным мультипликатором.

Он показывает абсолютное изменение в долгосрочном периоде 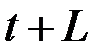 результата  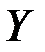под влиянием изменения на 1 единицу фактора .

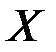Относительные коэффициенты модели с распределённым лагом вычисляются по формуле

.

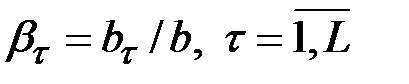Если все коэффициенты 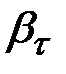 имеют одинаковые знаки, то для любого  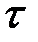имеем соотношение     

.

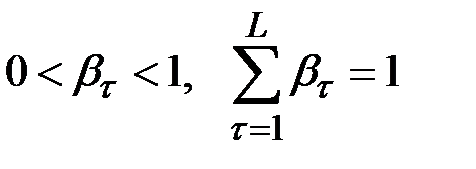В этом случае относительные коэффициенты 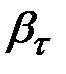 являются весами для соответствующих коэффициентов .

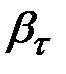Каждый из них измеряет долю общего изменения результативного признака в момент времени .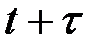

Зная величины 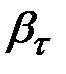, с помощью стандартных формул можно определить ещё две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага.

Средний лаг модели определяется по формуле средней арифметической взвешенной 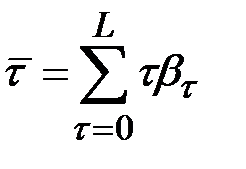 и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени .

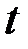Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.

Медианный лаг – это величина лага, для которого

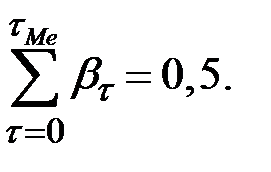
Это тот период времени, в течение которого с момента времени 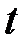 будет реализована половина общего воздействия фактора на результат.

Изложенные выше приёмы анализа параметров модели с распределённым лагом действительны только в предположении, что все коэффициенты при текущем и лаговых значениях исследуемого фактора имеют одинаковые знаки.

Это предположение вполне оправдано с экономической точки зрения: воздействие одного и того же фактора на результат должно быть однонаправленным независимо от того, с каким временным лагом измеряется сила или теснота связи между этими признаками.

Однако на практике получить статистически значимую модель, параметры которой имели бы одинаковые знаки, особенно при большой величине лага 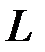, чрезвычайно сложно.

Применение обычного метода наименьших квадратов к таким моделям в большинстве случаев затруднительно по следующим причинам.

1. Текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом.

Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов.

2. При большой величине лага снижается число наблюдений, по которым строится модель, и увеличивается число её факторных признаков. Это ведёт к потере числа степеней свободы в модели.

3. В моделях с распределённым лагом часто возникает проблема автокорреляции остатков.

Вышеуказанные обстоятельства приводят к значительной неопределённости относительно оценок параметров модели, снижению их точности и получению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно.

Поэтому на практике оценку параметров моделей с распределённым лагом проводят в предположении определённых ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.