Временные ряды называются «белым шумом», если лежащая в их основе переменная имеет среднюю, равную нулю, постоянную дисперсию и нулевую корреляцию последовательных наблюдений (нулевую автокорреляцию).
Примером «белого шума» являются остатки в регрессионной модели, полученной методом наименьших квадратов.
Если переменная «белого шума» подчиняется нормальному распределению, то имеем дело с гауссовским белым шумом.
Авторегрессионным называется процесс, при котором значение ряда находится в линейной зависимости от предыдущих значений.
Если анализируемый динамический процесс зависит от значений, отстоящих от 1 до p временных шагов назад, то это авторегрессионный процесс (autoregressive process) порядка p, то есть AR(p).
Например, AR(3) можно отобразить следующей зависимостью:
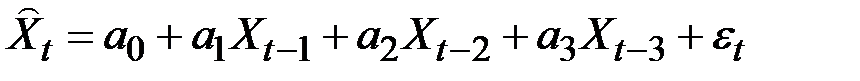 ,
,
где 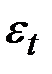 – остаток (ошибка, точность) регрессионной модели.
– остаток (ошибка, точность) регрессионной модели.
В модели скользящей средней (moving average process) моделируемая величина задаётся линейной функцией от прошлых ошибок, то есть разностей между прошлыми смоделированными значениями и прошлыми фактическими наблюдениями.
Например, модель MA(3) имеет вид
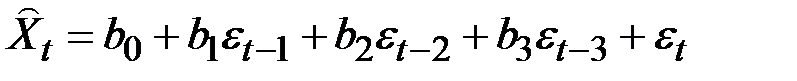 ,
,
где 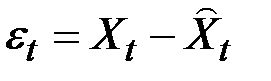 .
.
Авторегрессионная модель скользящей средней ARMA(p , q) имеет p временных шагов в авторегрессионном процессе и q интервалов в модели скользящей средней.
Например, ARMA(3,3) выглядит следующим образом:
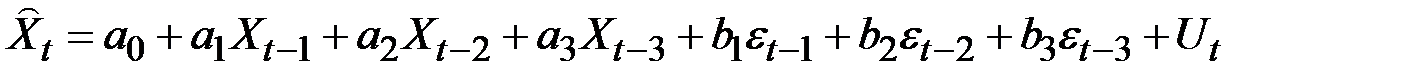 ,
,
где 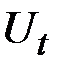 – остаточный член ошибки в данном уравнении.
– остаточный член ошибки в данном уравнении.
Авторегрессионный процесс и процесс скользящей средней предполагают, что анализируемые данные являются стационарными.
Интегрирование процесса I(d) означает, какого порядка d разности 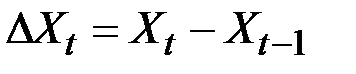 должны быть рассчитаны для того, чтобы получить стационарный временной ряд.
должны быть рассчитаны для того, чтобы получить стационарный временной ряд.
Если ряд уже стационарный, то есть для него не требуется вычисление разности, то такой ряд называется интегрированным рядом нулевого порядка I(0).
Если имеем ряд I(0), то его дисперсия будет конечна.
Изменения рассматриваемой переменной будут иметь только промежуточное влияние на временной ряд.
Коэффициенты автокорреляции будут постепенно убывать таким образом, что их сумма станет конечной.
Если же имеем ряд I(1), то изменения будут иметь постоянный эффект, дисперсия с течением времени будет возрастать до бесконечности.
Построение моделей с переменными I(1) может привести к видимой, но ложной корреляции, которую ошибочно можно принять за причинную связь, в то время как такой связи на самом деле нет.
И об этом может сказать корреляция рядов I(0).
7. Авторегрессионные интегрированные модели скользящей средней объединяют в себя процессы интегрирования, авторегрессии и скользящего среднего.
Если перед применением ARMA необходимо определить разности уровней с целью получения стационарного ряда, то надо знать порядок d этих разностей.
Процесс ARIMA (p,d,q) (autoregressive integrated moving average process) обладает тремя параметрами:
p – порядок авторегрессии;
d – порядок предварительно определяемых разностей;
q – порядок скользящей средней в модели.
Частные случаи
ARIMA (0,0,0):
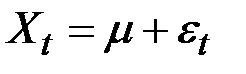 (если
(если 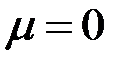 , то это «белый шум»),
, то это «белый шум»),
где 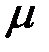 – средний уровень шума;
– средний уровень шума; 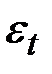 – ошибка.
– ошибка.
ARIMA (1,0,0):
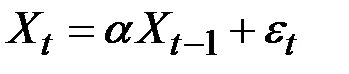 , ARIMA (1,0,0) = AR(1),
, ARIMA (1,0,0) = AR(1),
где 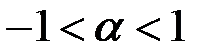 ;
; 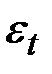 – элемент белого шума.
– элемент белого шума.
Если 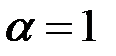 , то процесс не будет стационарным и потребуется вычисление разностей.
, то процесс не будет стационарным и потребуется вычисление разностей.
Это будет пример ARIMA (0,1,0), то есть процесс вида
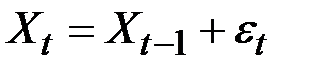 (случайное блуждание).
(случайное блуждание).
ARIMA (0,0,1):
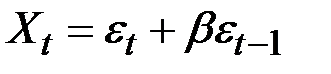 .
.
ARIMA (1,0,1):
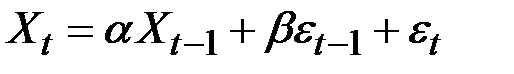 .
.
Дата: 2019-03-05, просмотров: 613.