Марковские процессы обладают тем свойством, что в отличие от случайных процессов общего вида для их полной характеристики достаточно знать только двумерные законы распределения.
Рассмотрим некоторую экономическую систему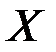 
с дискретными состояниями 
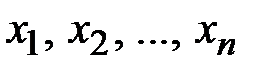, которая переходит из состояния в состояние под влиянием каких–то случайных событий (приход клиента в фирму, вызовы на телефонной станции, выходы из строя элементов аппаратуры, открытие отдела или филиала фирмы, прибытие грузовых или пассажирских составов на железнодорожную станцию, сбои вычислительной машины, неисправности в системе автоматики и т.д.).
Говорят, что в системе Х происходит случайный процесс, если она с течением времени может под влиянием случайных факторов переходить из состояния в состояние. В системе протекает случайный процесс с дискретным временем, если переходы из состояния в состояние могут происходить только в строго определённые, разделённые конечными интервалами моменты времени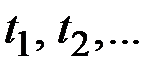 
.
Случайные процессы с непрерывным временем характеризуются тем, что переход системы из состояния в состояние возможен в любой момент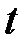 
.
Система называется системой с дискретными состояниями, если она имеет счётное (в частном случае – конечное) множество возможных состояний и переход из одного состояния в другое осуществляется скачком.
Возможные состояния системы наглядно изображаются с помощью так называемого графа состояний, на котором состояния системы изображены прямоугольниками (кружками), а возможные переходы системы из состояния в состояние – стрелками, соединяющими соответствующие прямоугольники.
Случайный процесс с дискретными состояниями называется марковским процессом, если все вероятностные характеристики процесса в будущем зависят лишь от того, в каком состоянии этот процесс находится в настоящий момент времени, и не зависит от того, каким образом этот процесс протекал в прошлом («будущее зависит от прошлого только через настоящее»).
Следует заметить, что случайный процесс, любые ординаты которого являются независимыми случайными величинами, полностью определяется одномерным законом распределения своих ординат.
В частности, для случая непрерывных величин – плотностью вероятности ординаты этого процесса, взятой в момент времени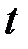 
.
Очевидно, что вследствие отсутствия вероятностной связи между ординатами такого процесса его корреляционная функция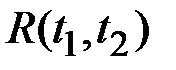 
отлична от нуля только при 
.
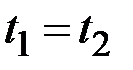Строго говоря, процессов с независимыми ординатами в природе не существует, так как все процессы, соответствующие реальным явлениям, обладают известной плавностью и, следовательно, соседние ординаты таких процессов не могут быть независимыми.
Для марковских случайных процессов полной характеристикой является двумерный закон распределения ординат процесса.
Определение марковского процесса можно записать и в другом виде: если для любых моментов времени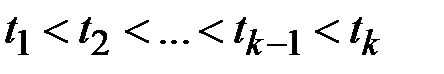 
справедливо соотношение
,
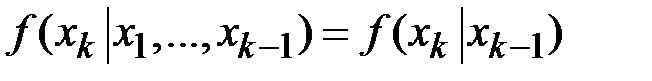то такой процесс называется марковским.
Плотность вероятности ординат марковского случайного процесса любого порядка может быть выражена через условные двумерные плотности вероятностей типа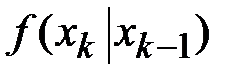 
и плотность вероятности 
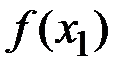первой ординаты. Однако и условные двумерные законы распределения однозначно выражаются через двумерные законы распределения.
Если обозначить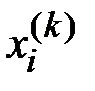 
событие, состоящее в том, что после 
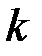шагов система находится в состоянии 
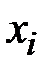, то случайный процесс, происходящий в этой системе, можно представить как последовательность (цепочку) событий, например, 
.
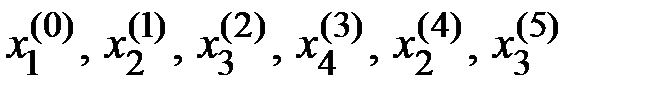Такая случайная последовательность называется марковской цепью, если для каждого шага вероятность перехода из любого состояния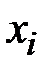 
в любое 
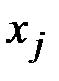не зависит от того, когда и как система пришла в состояние .
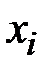Для любого шага (момента времени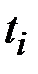 
) существуют какие–то вероятности перехода системы из любого состояния в любое другое (некоторые из них могут быть равны нулю, если переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии.
Эти вероятности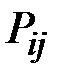 
называются переходными вероятностями марковской цепи.
Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага.
В противном случае марковская цепь называется неоднородной.
Если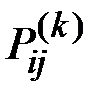 
– вероятность перехода системы из состояния 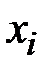в состояние 
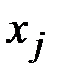на 
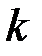–м шаге, то вероятность того, что система 
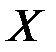будет находиться после 
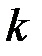шагов в состоянии 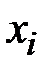выражается формулой
; 
.
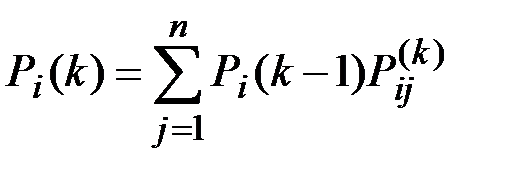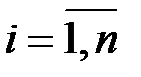Широкое приложение марковские процессы находят в построении моделей систем массового обслуживания.
Другое типичное приложение марковских процессов в экономике – прогнозирование спроса.
Случайное блуждание
Случайное блуждание – это случайный процесс специального вида, который можно интерпретировать как модель, описывающую перемещение частицы в некотором фазовом пространстве под воздействием какого–либо случайного механизма.
Фазовым пространством обычно бывает m–мерное евклидово пространство или целочисленная решётка в нём.
Случайные механизмы могут быть различными.
Чаще рассматривают блуждания, порождённые суммированием независимых случайных величин или цепями Маркова.
Траектории простейших блужданий в случае m = 1 описываются начальным положением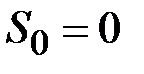 
и последовательностью сумм
,
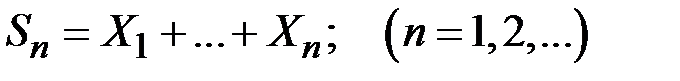где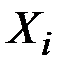 
– независимы и имеют распределение Бернулли
.
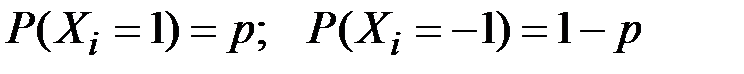Значение Sn можно интерпретировать как выигрыш одного из двух игроков после n партий в игре, в которой этот игрок в каждой из партий выигрывает один рубль с вероятностью p и проигрывает его с вероятностью 1 – p.
Если игра ведётся с помощью подбрасывания симметричной монеты, то следует положить p = 0,5.
В этом случае имеем блуждание Бернулли, или симметричное блуждание.
При допущении, что начальный капитал 1–го игрока равен b, а 2–го игрока равен a, игра закончится, когда блуждающая частица (с координатами S1, S2, …) впервые коснётся одного из уровней a или – b. В этот момент один из игроков разорится.
Это классическая задача о разорении, в которой барьеры в точках a и – b можно рассматривать как поглощающие.
В приложениях, связанных с теорией массового обслуживания, частица вблизи барьеров может вести себя иначе.
Например, если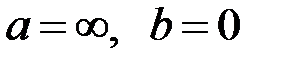 
, то положение 
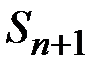блуждающей частицы в момент (n + 1) описывается соотношением
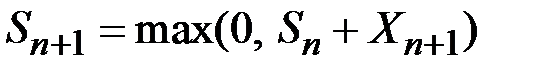
и барьер в точке 0 можно назвать задерживающим. Существуют и другие возможности для поведения частицы вблизи барьеров.
Если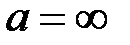 
, то имеем блуждание с одной границей.
Если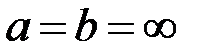 
, то получим неограниченное блуждание.
Изучение описанных случайных блужданий происходит обычно с помощью аппарата дискретных цепей Маркова и, в частности, путём исследования соответствующих уравнений в конечных разностях.
Пусть, например, Pk есть вероятность разорения первого игрока в задаче о разорении, если его капитал равен k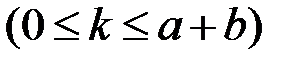 
, а суммарный капитал обоих игроков фиксирован и равен a + b.
Тогда из формулы полной вероятности (по первому скачку) следует, что Pk удовлетворяет уравнению
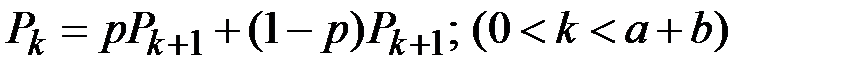
и граничным условиям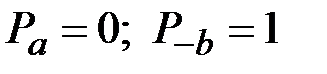 
.
Отсюда получают
.
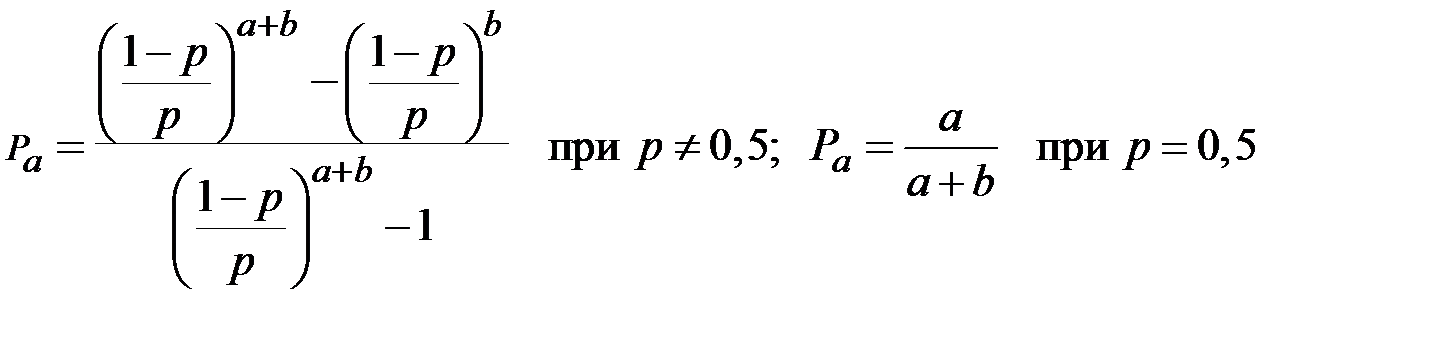Вторая из этих формул показывает, что даже «безобидная» игра (в которой оба игрока имеют одинаковые шансы) приводит к разорению с вероятностью, близкой к 1, если капитал 2–го игрока a велик по сравнению с b.
На практике можно считать, что случайное блуждание – это стохастический процесс, в котором изменения уровня достигаются прибавлением случайной переменной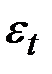 
с постоянной дисперсией и средней, равной нулю:
,
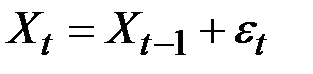где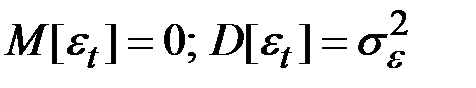 
.
При этом
.
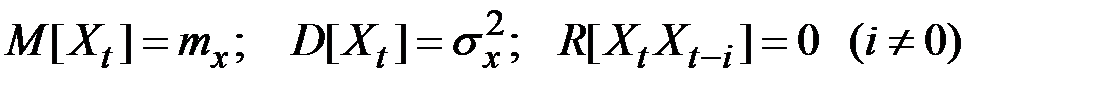Процесс случайного блуждания характеризуется нулевой корреляцией отдельных наблюдений.
Иногда случайное блуждание может включать элемент сдвига (тренд):
.
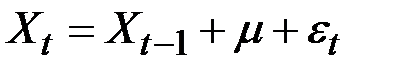Случайное блуждание имеет два важных свойства: свойство Маркова и мартингальное свойство.
Свойство Маркова состоит в том, что вся информация, необходимая для определения условий вероятности будущего (следующего) значения переменной, содержится в текущем значении (состоянии) этой переменной, а не в историческом распределении её вероятности.
Мартингальное свойство означает, что условное ожидание будущего значения величины равно текущему значению переменной.
Мартингал
Мартингал – это более общий стохастический процесс, чем случайное блуждание, так как в мартингале изменения задаются значением случайной переменной с нулевым математическим ожиданием, но не обязательно с постоянной дисперсией.
И изменения не должны быть независимыми.
Мартингал – стохастическая последовательность
,
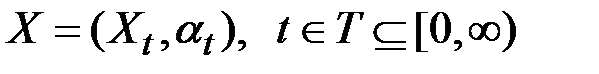заданная на вероятностном пространстве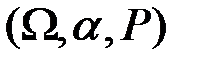 
с выделенным на нем неубывающим семейством σ–алгебр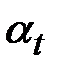 
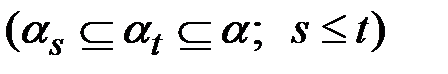, такая, что 
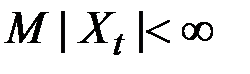, Xt являются 
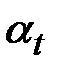–измеримыми и 
.
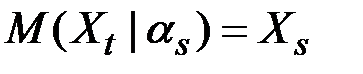Родственными понятиями являются стохастические последовательности, образующие субмартингал, для которых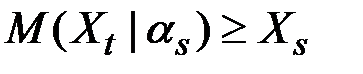 
, и супермартингал, для которых 
.
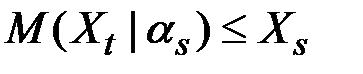Например, если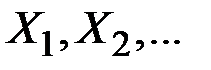 
– последовательность независимых случайных величин с нулевым математическим ожиданием, то 
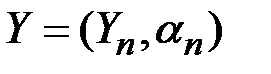с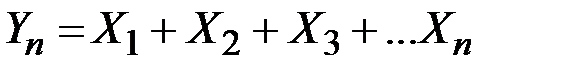 
, 
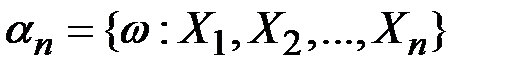является мартингалом при 
.
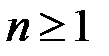Термин «мартингал» возник из игровой практики, в которой мартингалом называлась система игры со следующими правилами.
Пусть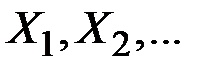 
– последовательность независимых случайных величин, соответствующих схеме Бернулли, то есть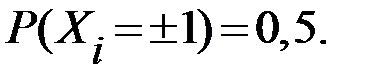 
И пусть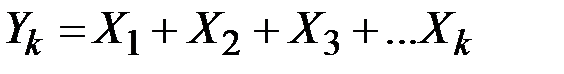 
;
;
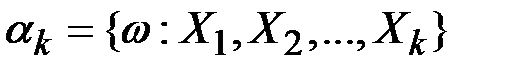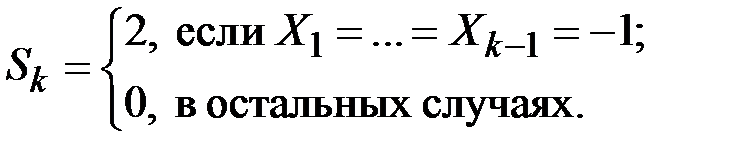
Игрок выигрывает единицу капитала, если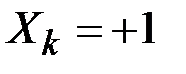 
и проигрывает единицу, если 
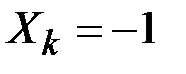, а Sk – величина его ставки в k–й партии.
Игровой смысл функции Sk состоит в том, что игрок увеличивает ставку вдвое при проигрыше и прекращает игру при первом выигрыше.
Здесь последовательность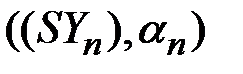 
образует мартингал (субмартингал), где
.
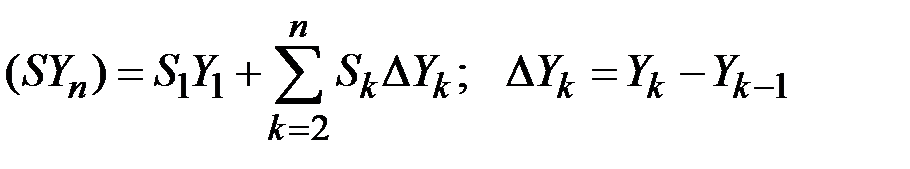На практике случайные блуждания с положительным сдвигом (трендом)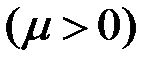 
называется субмартингалом, а с отрицательным сдвигом 
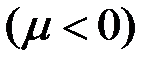– супермартингалом.
Непрерывные во времени случайные блуждания называются диффузионным процессом.
4. Основной процесс Винера (броуновское движение)
Это разновидность марковского процесса.
Здесь изменение показателя X за малый промежуток времени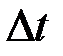 
определяется зависимостью
,
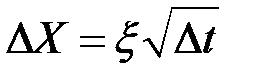где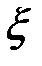 
– нормированная нормальная случайная величина N(0,1).
В силу нормальности величины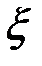 
величина 
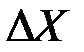тоже будет нормально распределена со средней, равной нулю, дисперсией 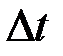и средним квадратическим отклонением 
.
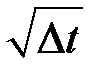В пределе можно записать
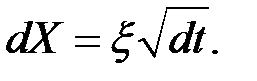
В основном процессе Винера переменная X изменяется случайным образом на величину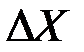 
, которая зависит от другой случайной величины 
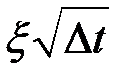, имеющей среднюю, равную нулю, и среднее квадратическое отклонение 
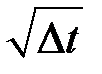. Разные значения 
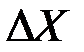независимы и распределены по закону 
.
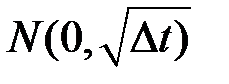Если дисперсия отдельной величины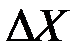 
равна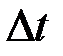 
, то дисперсия за более длинный промежуток времени (сумму периодов) будет равна 
.
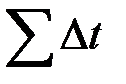Степень изменчивости уровня показателя X увеличивается с увеличением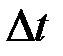 
, тогда как степень изменчивости на каждом шаге постоянна.
Процессы Винера часто применяют для описания экономических процессов, в частности финансовых показателей.
Применение броуновского движения к описанию цен активов затруднено по трём причинам.
1. Активы характеризуются различными степенями волатильности (изменчивости в единицу времени). В броуновском движении волатильность постоянна (одна).
2. Активы имеют положительное ожидаемое среднее значение дохода. В броуновском движении среднее значение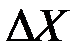 
предполагается равным нулю, а следовательно и будущая цена не будет отличаться от настоящей ( 
).
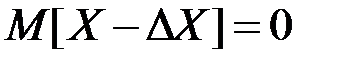3. В броуновском движении предполагается, что абсолютные изменения в цене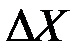 
независимы от величины X.
Однако на практике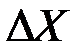 
зависит от X.
Чаще независимыми от X являются пропорциональные процентные изменения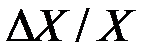 
.
Указанные выше три замечания (проблемы) учитываются следующим образом.
1. Конкретный актив имеет свою конкретную степень волатильности (изменчивости, риска) 
.
Следовательно, исходное уравнение можно записать в виде
.
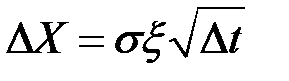Здесь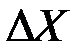 
имеет распределение 
.
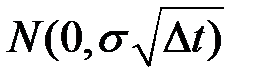2. Требование положительности ожидаемого дохода удовлетворяется добавлением тенденции (тренда) к основному процессу Винера, что приводит к обобщённому процессу Винера
.
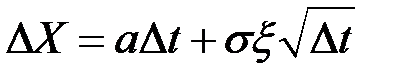Параметр тенденции a представляет собой изменение X за малый промежуток времени dt (скорость тенденции, абсолютный доход за единицу времени).
Величина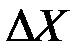 
имеет распределение 
.
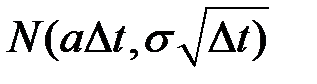Малое изменение в цене актива за малый временной интервал можно смоделировать следующим стохастическим дифференциальным уравнением:
.
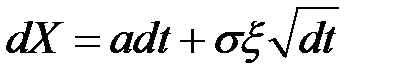Обобщённый процесс Винера может рассматриваться как непрерывный во времени эквивалент субмартингального процесса, включающего в себя детерминированный тренд и основной стохастический процесс Винера.
3. На практике чаще используется процентная ставка доходности, зависящая от риска и не зависящая от уровня цены актива. При этом абсолютный доход является функцией цены актива, но ставка дохода не должна зависеть от цены актива.
Стохастический процесс Ито
Процессе Ито является обобщённым процессом Винера, в котором параметры a (ожидаемый доход) и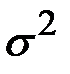 
являются функциями от переменных X и t (цены актива и времени):
.
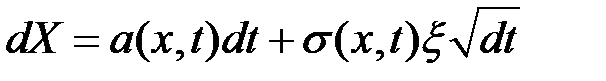Пусть r – ожидаемая ставка доходности (десятичная дробь).
Тогда rX будет абсолютным доходом.
Для малого промежутка времени 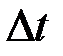ожидаемый абсолютный доход будет равен величине 
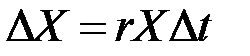, что в пределе даёт соотношение
.
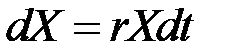Разделив обе части равенства на X, получим ставку доходности
.
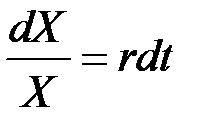Отсюда следует, что абсолютное изменение цены актива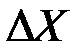 
является функцией цены актива 
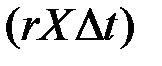, а ставка доходности 
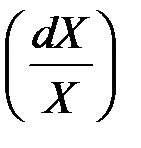не зависит от цены актива.
Можно установить функциональную зависимость абсолютного ожидаемого дохода от цены актива, но степень неопределённости этого дохода в течение малого периода времени будет независима от цены актива.
Это означает, что инвестор испытывает одинаковую неопределённость относительно будущих доходов независимо от того, стоит актив 1 тыс. или 8 тыс. руб.
Следовательно,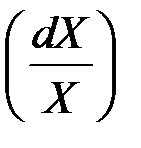 
является функцией от rdt и 
.
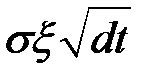Эти два слагаемых и составляют процесс Ито (геометрическое броуновское движение):
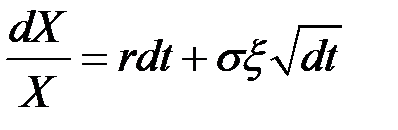или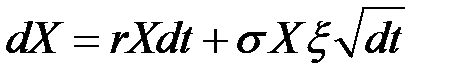 
.
В этом процессе ожидаемый абсолютный доход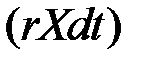 
будет тем больше, чем выше цена актива.
Дисперсия фактических изменений цены актива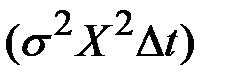 
зависит от величины квадрата этой цены.
Величина dX имеет распределение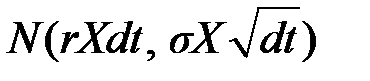 
, а величина 
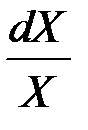имеет распределение 
.
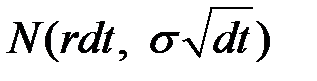Если переменная Y является функцией переменной X, которая следует процессу Ито в форме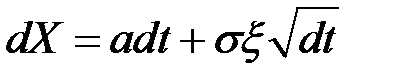 
, то и переменная Y будет следовать процессу Ито в форме
.
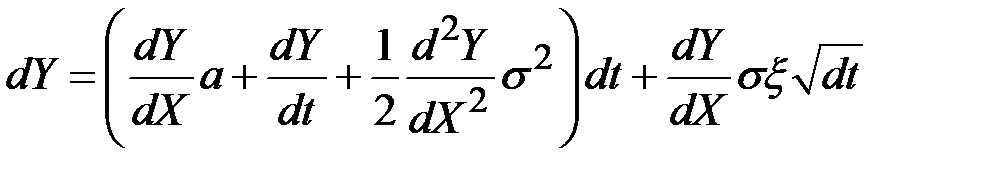Составным элементом здесь также является основной процесс Винера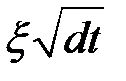 
.
Переменная Y имеет скорость тенденции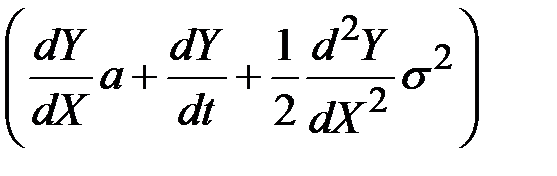 
и норму изменчивости (волатильности) 
.
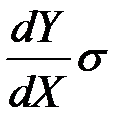В частности, если X – цена актива, лежащего в основе производных финансовых инструментов (опционы, фьючерсы и др.),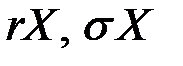 
– ожидаемые доход и среднее квадратическое отклонение актива соответственно, то переменная Y, являющаяся функцией от X и t, будет следовать процессу Ито в форме
.
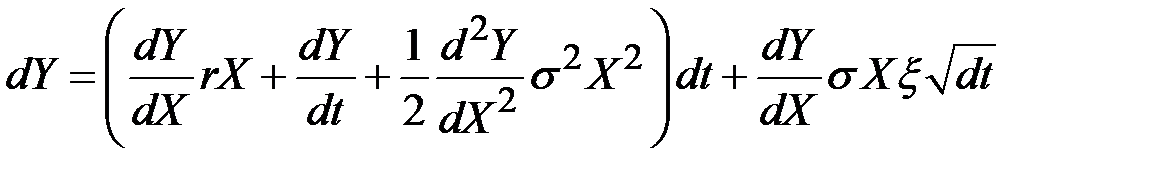Это выражение можно использовать при определении стоимости производных финансовых инструментов.
Процессы Ито для основного актива и для производной ценной бумаг содержат стохастический элемент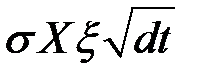 
, но в разных пропорциях.
Следовательно, можно заказать длинную позицию (купить) по основной переменной X и короткую (продать) по производной переменной Y таким образом, что эти два стохастических процесса исключат друг друга.
В результате портфель ценных бумаг, состоящий из длинной позиции по X и короткой по Y, может стать безрисковым и должен (будет) иметь безрисковую процентную ставку.
Это означает, что безрисковой процентной ставки может быть достаточно для дисконтирования будущей стоимости и приведения её к текущей.
Построим портфель П, состоящий из одной короткой позиции по Y и длинной позиции по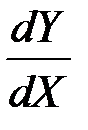 
единиц основного актива X.
Тогда изменение стоимости портфеля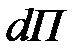 
будет равно
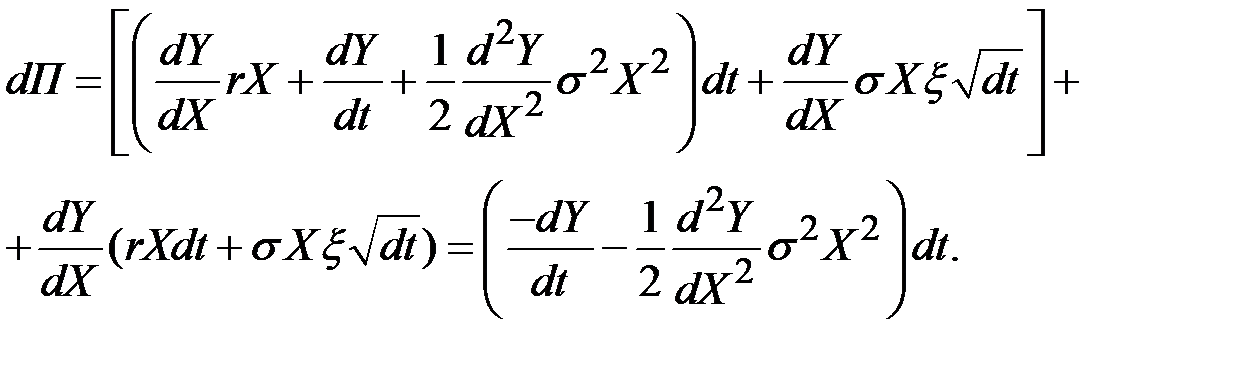
Так как портфель является безрисковым в каждом коротком промежутке времени, он имеет мгновенную безрисковую процентную ставку r0.
Поэтому любое изменение П за малый промежуток должно быть равно произведению безрисковой процентной ставки и стоимости безрискового портфеля за тот же малый временной интервал.
Тогда
.
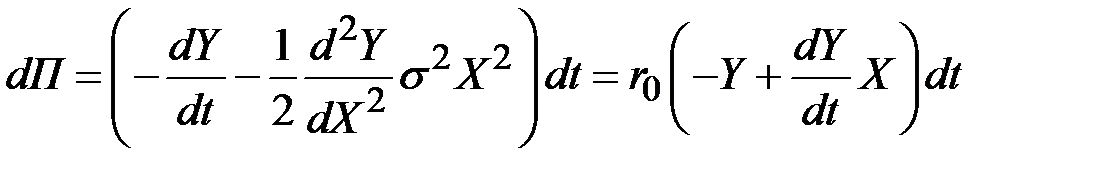Раскрыв скобки и упростив, получим
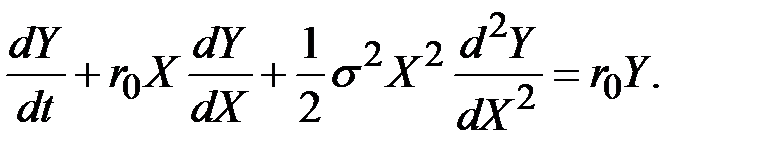
Это означает, что ожидаемый доход или скорость тенденции r может быть заменена безрисковой процентной ставкой r0.
Тогда отпадает необходимость в том, чтобы знать ожидаемую ставку дохода по основному активу в процессе определения цены производного финансового инструмента.
Необходимо ещё знать 
основной переменной (фактически должны знать распределение вероятностей основного актива).
Последнее уравнение – уравнение в частных производных, выведенное Блэком и Сколсом для определения стоимости любого производного финансового инструмента.
Для разных типов таких инструментов уравнение имеет разные решения, которые зависят от ограничивающих условий для каждого из этих типов инструментов.
Уравнение описывает скорость изменения переменной (цены), но не описывает уровень значения этой переменной.
Такую информацию и представляют ограничивающие условия.
Описывая цены активов, часто делают два предположения (допущения):
1) цены активов следуют процессу Ито;
2) цены активов распределены логарифмически нормально и, как следствие, непрерывно наращённый доход распределён по нормальному закону.
Можно показать, что эти два допущения неразрывно связаны друг с другом.
Пусть цена актива X следует процессу Ито в форме
.
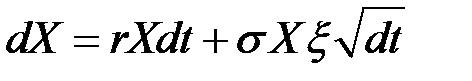Натуральный логарифм этой переменной нормально распределён
,
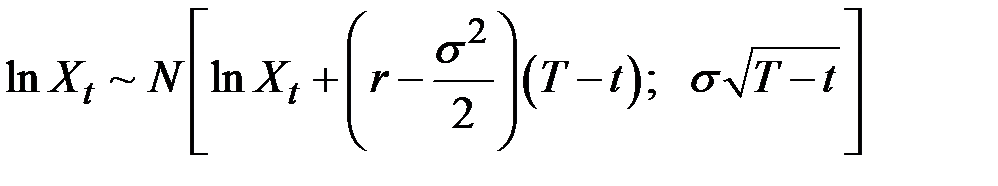где t – текущее время;
T – будущая точка во времени;
(T – t) – период времени анализа цены актива.
Пусть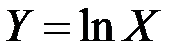 
.
Переменная Y также будет следовать процессу Ито, в котором
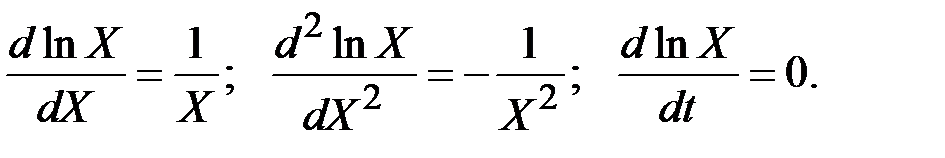
Подставляя эти выражения в формулу процесса Ито для Y, получим
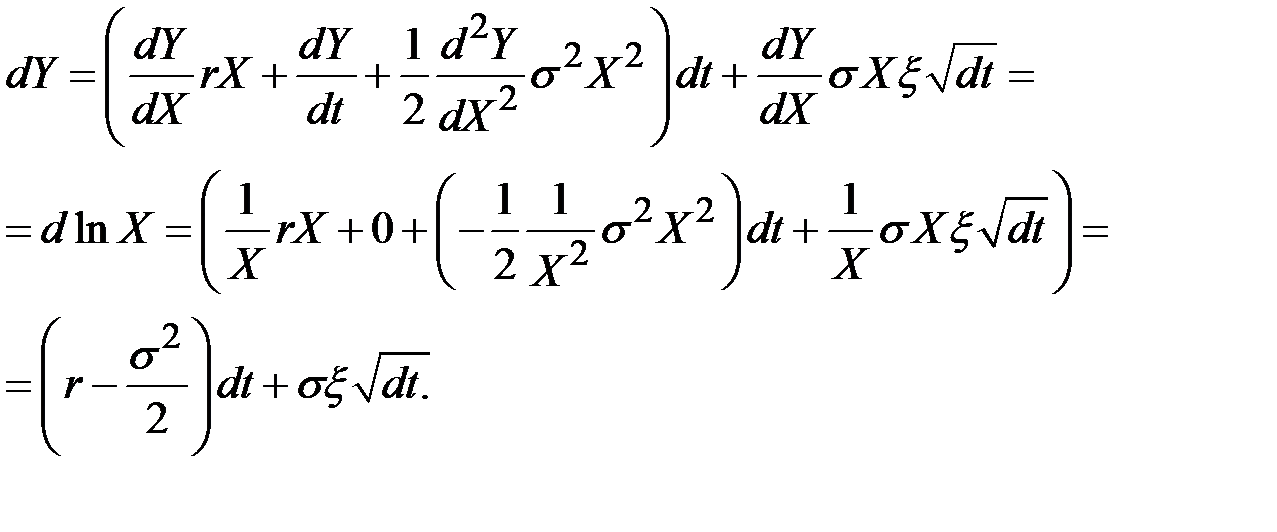
Таким образом, lnX следует процессу Винера.
Дата: 2019-03-05, просмотров: 549.
