Определение. Пусть функции
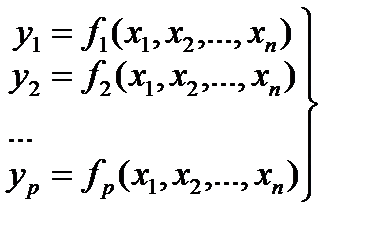
определены и дифференцируемы в открытой области D . Одна из этих функций, например, f1 называется функционально зависящей в области D от остальных, если существует дифференцируемая функция Ф такая, что
f1(x) = Ф(f2(x),f3(x),…,fp(x)), " x Î D.
Функции y1,…, yp называются функционально зависимыми в области D , если одна из них зависит в D от остальных. В противном случае система называется независимой.
Теорема 1 (необходимое условие зависимости функций). Пусть дана система функционально зависимых в области D функций из класса C1
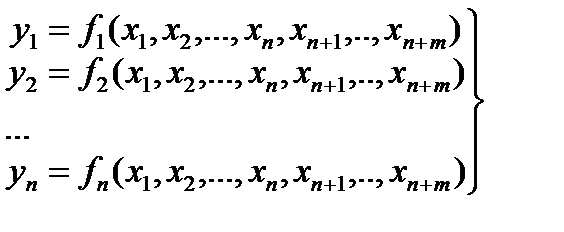 .
.
Тогда в любой точке D ранг rang 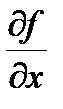 < n .
< n .
Доказательство. Предположим для определенности, что
fn(x) = Ф(f1(x),…, fn -1(x)), " x Î D .
Тогда по правилу дифференцирования сложных функций
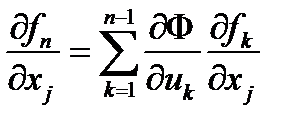 .
.
Эти равенства означают, что n –я строка матрицы Якоби является линейной комбинацией остальных строк. Коэффициентами этой линейной комбинации являются частные производные 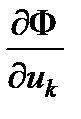 .
.
Следствие 1. m =0 и система зависимая. Тогда якобиан 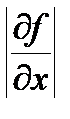 =0 в области D .
=0 в области D .
Следствие 2 (достаточное условие функциональной независимости). Пусть rang 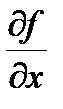 = n в точке x0 , тогда система независима в D .
= n в точке x0 , тогда система независима в D .
Замечание. Отметим, что условие функциональной зависимости связано с областью D . Система может оказаться независимой в D и зависимой в некоторой части этой области.
Теорема 2 (достаточное условие функциональной зависимости). Если
rang 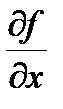 £ r < n в любой точке области D , а в некоторой точке x 0 ранг rang
£ r < n в любой точке области D , а в некоторой точке x 0 ранг rang 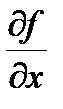 = r
= r
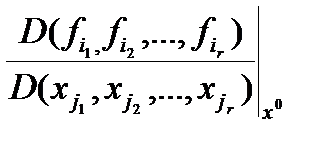 ¹ 0.
¹ 0.
Тогда
1) все r функций 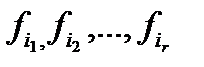 являются независимыми в области D ,
являются независимыми в области D ,
2) существует окрестность точки x0, в которой любые из оставшихся функций зависят от выбранных r функций.
6.5. Условный экстремум
Условный экстремум. Необходимые и достаточные условия условного экстремума.
Необходимые условия
Рассмотрим функцию
u = f(x1, x2,…., xn , xn +1,…, xn + m), или кратко u = f(x) (6.12)
определенную в области D Ì Rn + m . Обозначим через D1 множество точек из D , удовлетворяющих n условиям
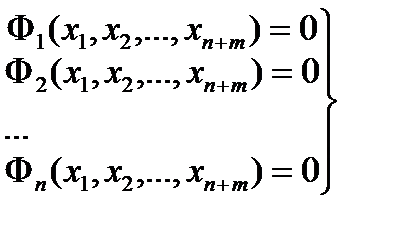 , Ф(x)=0. (6.13)
, Ф(x)=0. (6.13)
Условия (6.13) назовем уравнениями связи.
Определение. Точка x0=( 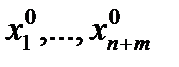 ) называется точкой условного максимума функции (6.12) при связях (6.13), если существует окрестность этой точки U(x0) такая, что
) называется точкой условного максимума функции (6.12) при связях (6.13), если существует окрестность этой точки U(x0) такая, что
"xÎU(x0)ÇD1 : f(x)< f(x0).
Аналогично определяется условный минимум и условный экстремум.
Введем обозначения p =(x1, x2,…, xn), q =(xn +1, xn +2,…, xn + m), x =( p , q)=(x1, x2,…, xn + m), p0=( 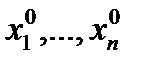 ), q0=
), q0= 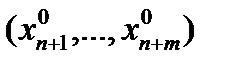 , x0=(, p0 ,q0)=(
, x0=(, p0 ,q0)=( 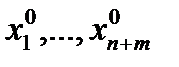 ). Будем предпологать, что ФÎ C1(U(x0)) и
). Будем предпологать, что ФÎ C1(U(x0)) и
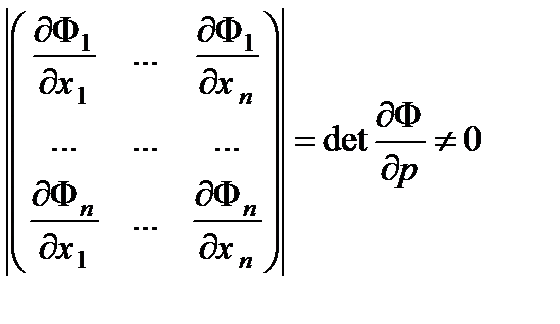 , в точке x0.
, в точке x0.
Можно считать, что якобиан отличен от нуля в U(x0 ). В этом случае в каждой точке этой окрестности выполнены условия теоремы существования и единственности системы функций, заданных неявно системой уравнений (6.13) и эту систему можно разрешить относительно p в окрестности точки q 0 = 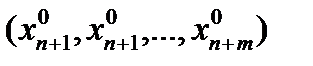
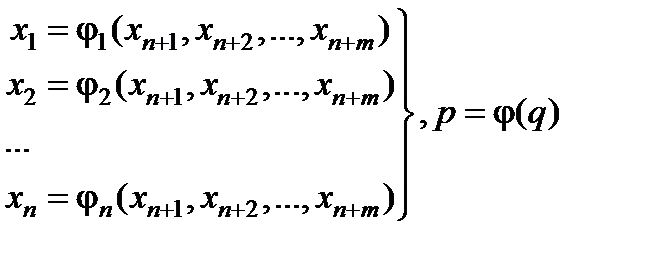 (6.14)
(6.14)
Таким образом, любая точка из области U(x0)ÇD1 может быть записана в виде
(j1(q),j2(q),…,jn(q), q).
Тогда необходимым и достаточным условием для условного экстремума в точке x0 будет «безусловный» экстремумом функции
F(q) = f(j1(q),j2(q),…,jn(q), q) в точке q0.
В силу этого необходимыми условиями условного экстремума будет условия
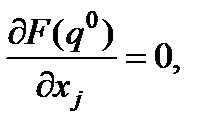 j = n +1, n +2,…, n + m .
j = n +1, n +2,…, n + m .
В частности,
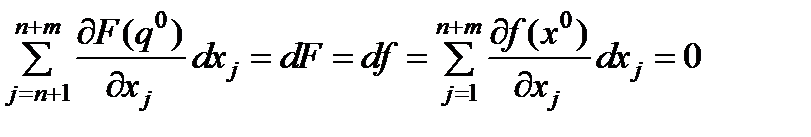 (6.15)
(6.15)
Продифференцируем тождества (6.13)
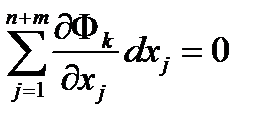 (6.16k)
(6.16k)
Умножим каждое уравнение (6.16k) на l k сложим их c уравнением (6.15). В результате получим
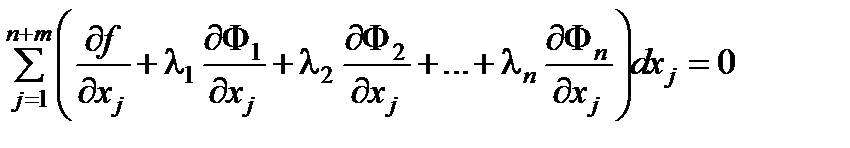 (6.17)
(6.17)
Выберем li так, чтобы множители при зависимых дифференциалах dxj (т.е. при j =1,2,…,n) обращались в 0
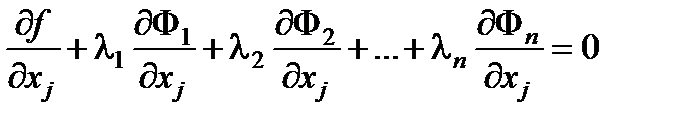 , j =1,2,…, n . (6.18)
, j =1,2,…, n . (6.18)
Это можно сделать в силу того, что 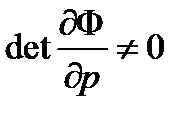 . Тогда из (6.17) получим
. Тогда из (6.17) получим
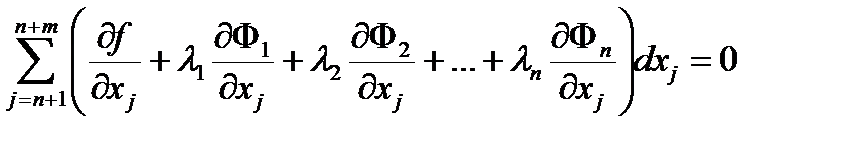 . (6.19)
. (6.19)
Так как dxj , j = n +1,…, n + m – дифференциалы независимых переменных, то из (6.19) следует, что все множители при этих дифференциалах равны нулю
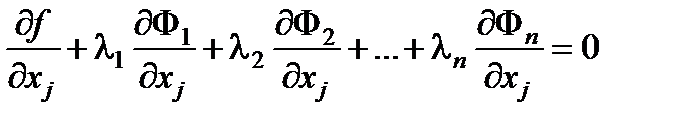 , j = n +1, n +2,…, n + m . (6.20)
, j = n +1, n +2,…, n + m . (6.20)
Таким образом, как это следует из (6.18), (6.20) для всех j будут выполнены равенства
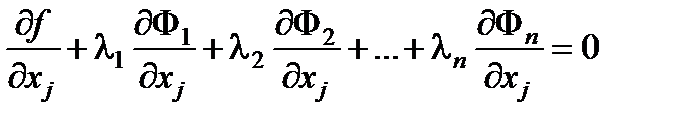 , j =1,2,…, n + m . (6.21)
, j =1,2,…, n + m . (6.21)
Поводя итог, можно сказать, что точка условного экстремума x0 должна удовлетворять системам уравнений (6.13), (6.21)
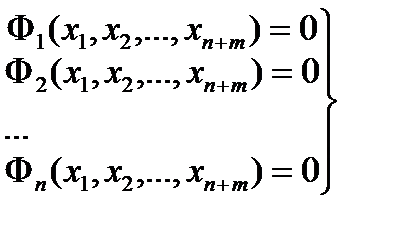 ,
,
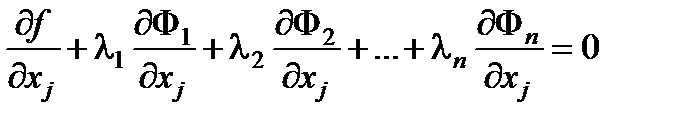 , j =1,2,…,n + m ,
, j =1,2,…,n + m ,
которые дают m +2n уравнений для определения m +2n неизвестных. Этими неизвестными являются: n + m координат точки x0 и n неопределенных множителей lj . Эти множители называются множителями Лагранжа. Доказанное утверждение сформулируем в виде теоремы
Теорема (необходимые условия для условного экстремума). Пусть функция
u = f(x1,…, xn + m)
определена в области D Ì Rn + m , x0 внутренняя точка D и заданы n непрерывно дифференцируемые связи
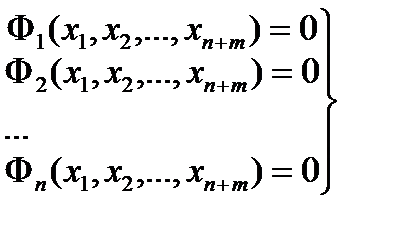 ,
,
причем
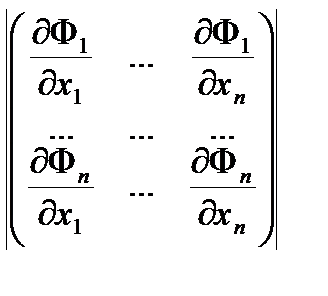 ¹0, в точке x0.
¹0, в точке x0.
Тогда в точке x0 выполнены условия
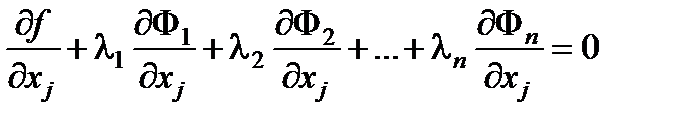 , j =1,…, n + m . (6.22)
, j =1,…, n + m . (6.22)
Замечание. При составлении уравнений (6.22) для поиска точек «подозрительных» на условный экстремум удобно использовать функцию Лагранжа
L = f + 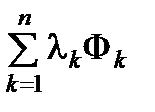 ,
,
условия (6.22) тогда запишутся в виде
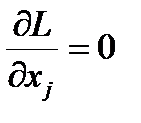 (или dL=0).
(или dL=0).
Достаточные условия
Пусть в точке x0= 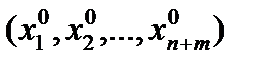 выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df = f(x) – f(x0) при условии, что xÎD1 (область, определяемая уравнениями связи). Для таких точек DFi = 0, поэтому Df = DL , и исследование поведения Df сводится к исследованию поведения приращения функции Лагранжа DL . По формуле Тейлора
выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df = f(x) – f(x0) при условии, что xÎD1 (область, определяемая уравнениями связи). Для таких точек DFi = 0, поэтому Df = DL , и исследование поведения Df сводится к исследованию поведения приращения функции Лагранжа DL . По формуле Тейлора
DL = 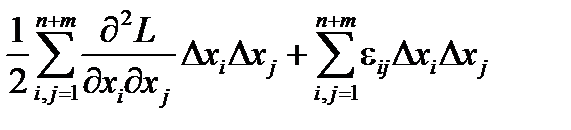 , eij ® 0 при Dxi ® 0.
, eij ® 0 при Dxi ® 0.
Если выразить приращения Dxi (i =1,…. n ) зависимых переменных через приращения Dxk (k = n +1,…. n + m) независимых переменных (это можно сделать, продифференцировав уравнения связи), то можно получить выражение для DL следующего вида
DL = 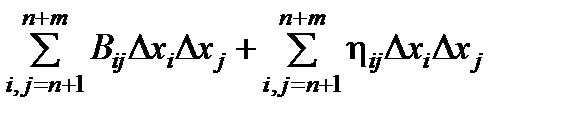 , hij ®0 при Dxi ®0.
, hij ®0 при Dxi ®0.
После этого можно использовать достаточные условия, выведенные для «безусловных» экстремумов по квадратичной форме 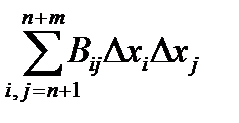 .
.
Пример 1. Частный случай
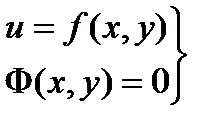 , L = f +lF, dL =0 (необходимое условие)
, L = f +lF, dL =0 (необходимое условие)
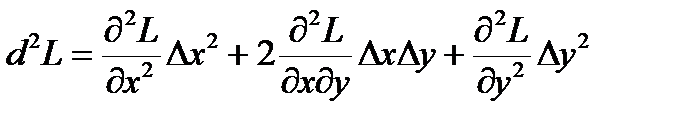 , DL =
, DL = 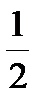 d 2 L +er2,
d 2 L +er2,
0= dF= 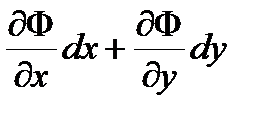 , dy =–
, dy =– 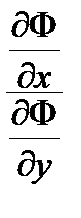 dx , после подстановки получим
dx , после подстановки получим
DL = BDx2+ o(Dx2). В зависимости от полученного коэффициента B можно сделать вывод о наличии условного экстремума.
Пример 2.
u = x2+12xy +2y2, 4x2+ y2=25.
L=x2+12xy+2y2+l(4x2+y2–25), dL=(2x+12y+8lx)dx+(4y+12x+2ly)dy,
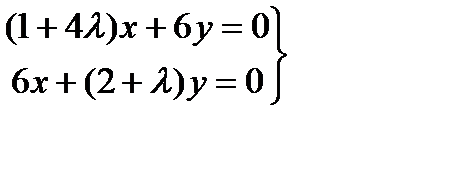 ,
, 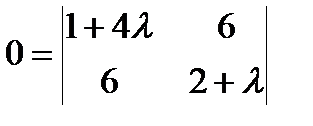 , 4l2+9l-34=0, l1,2=2;
, 4l2+9l-34=0, l1,2=2; 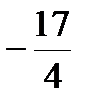 .
.
l1=2, 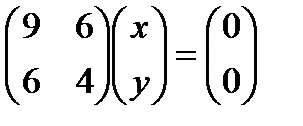 ,3x +2y =0, y =-
,3x +2y =0, y =- 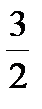 x ,
x ,
4x2+ 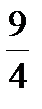 x2=25,
x2=25, 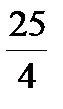 x2=25, x =±2,
x2=25, x =±2,
l1=2, точки (2,-3), (-2,3).
l2= 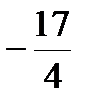 ,
, 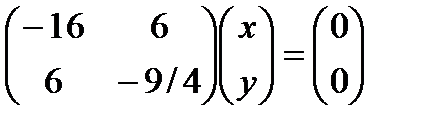 ,-8x +3y =0, y =
,-8x +3y =0, y = 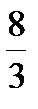 x , 4x2+
x , 4x2+ 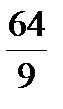 x2=25,
x2=25, 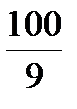 x 2=25, x = ±
x 2=25, x = ± 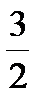 .
.
l1= 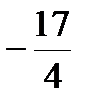 , точки (
, точки ( 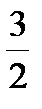 ,4), (-
,4), (- 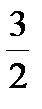 ,-4).
,-4).
d2L=(2+8l)dx2+24dxdy +(4+2l)dy2, 8xdx +2ydy =0, dy = -4 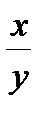 dx .
dx .
1) (2,-3), l=2
d2L =(2+16)dx2-24·4 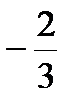 dx2+8·16
dx2+8·16 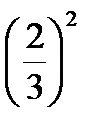 dx2=[18+64+…]dx2 минимум.
dx2=[18+64+…]dx2 минимум.
Пример 3 (3659). u = x – 2y + 2z , x2 + y2 + z2 = 1
L = x – 2y + 2z +l( x2 + y2 + z2 – 1)
dL =(1 + 2l x)dx +( – 2 + 2l y)dy +(2 + 2l z)dz,
d 2L = 2l dx2 + 2l dy2 + 2l dz2
1 + 2lx = 0, -1 + l y = 0, 1 + l z =0,
x = 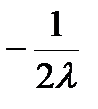 , y =
, y = 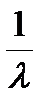 , z =
, z = 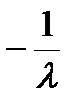 , подставляя в уравнение связи найдем l = ±3/2
, подставляя в уравнение связи найдем l = ±3/2
(-1/3, 2/3, -2/3), l = 3/2
(1/3, -2/3, 2/3) l = -3/2, дифференцируя уравнение связи получим
xdx + ydy + zdz = 0, dz = 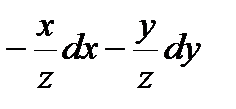 , dz2 = …,
, dz2 = …,
d 2L = … = 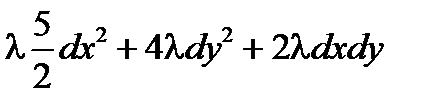 главные миноры
главные миноры 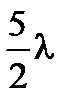 , 9l2.
, 9l2.
Дата: 2019-03-05, просмотров: 395.