Дана система

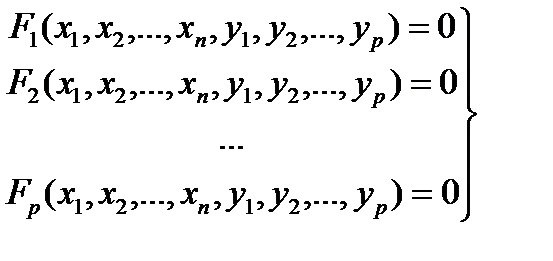                                          (6.8)

Будем предполагать, что выполнены условия теоремы существования и единственности неявной функции, заданной этой системой уравнений. Обозначим эту функцию y = f(x) . Тогда в некоторой окрестности точки x⁰ справедливы тождества

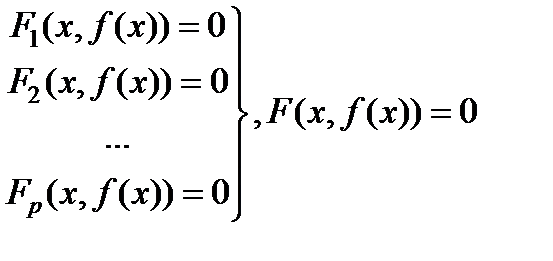
Дифференцируя эти тождества по x_j получим

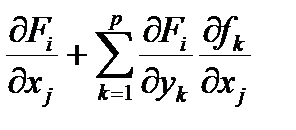=0.                                            (6.9)

Эти равенства можно записать в матричном виде

,

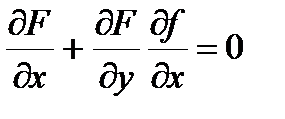или в развернутом виде

.

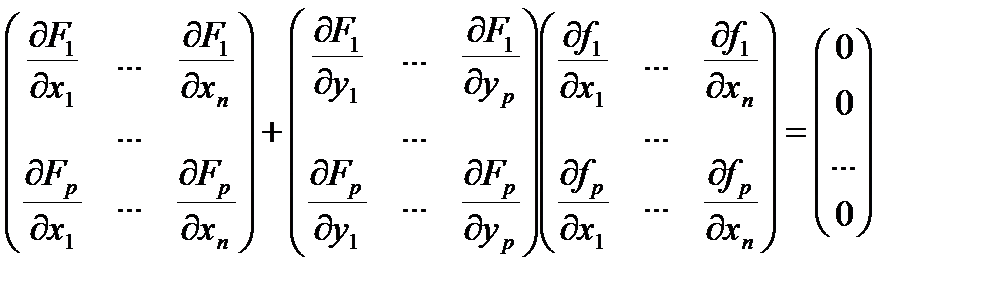Отметим, что переход от равенства F(x , f(x))=0 к 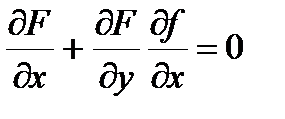, соответствует правилам дифференцирования для случая, когда x и y являются точками одномерного пространства. Матрица  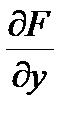по условию не вырождена, поэтому матричное уравнение  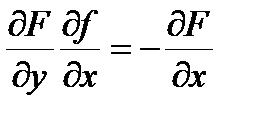имеет решение  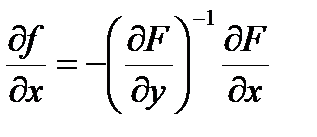. Таким образом, можно найти частные производные первого порядка неявных функций 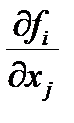. Для нахождения дифференциалов обозначим

dy = 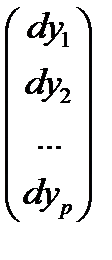, dx = 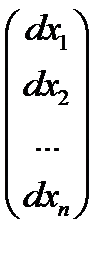, дифференцируя равенства (6.8), получим

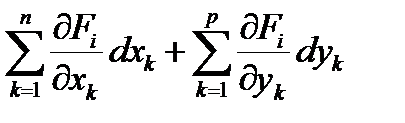=0 , 

или в матричном виде

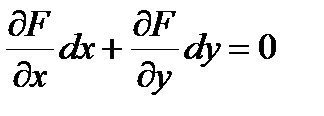.                                            (6.10)

В развернутом виде

.

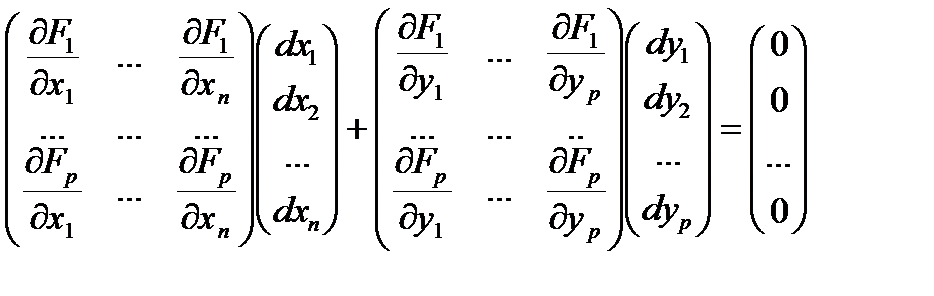Так же как и в случае частных производных, формула (6.10) имеем такой же вид, как и для случая одномерных пространств n =1, p =1. Решение этого матричного уравнения запишется в виде 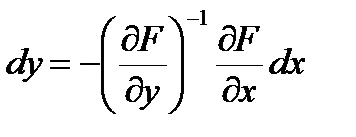. Для нахождения частных производных второго порядка нужно будет дифференцировать тождества (6.9) (для вычисления дифференциалов второго порядка дифференцировать нужно тождества (6.10) ). Таким образом, получим

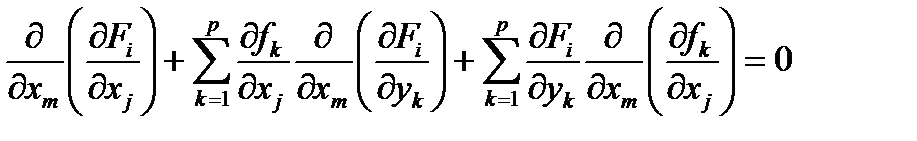
или

,

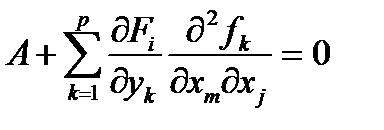где через A обозначены слагаемые, не содержащие искомые .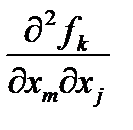

Матрицей коэффициентов этой системы для определения производных 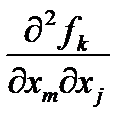служит матрица Якоби .

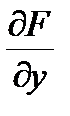Аналогичную формулу можно получить для дифференциалов. В каждом из этих случаев будет получаться матричное уравнение с той же матрицей коэффициентов 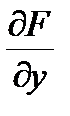 в системе уравнений для определения искомых производных или дифференциалов. То же самое будет происходить и при следующих дифференцированиях.

Пример 1. Найти 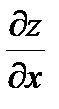, , 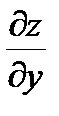 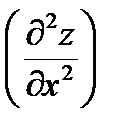в точке u =1, v =1.

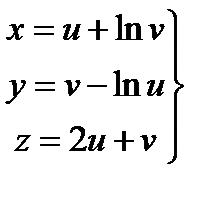
Решение. Дифференцируем заданные равенства

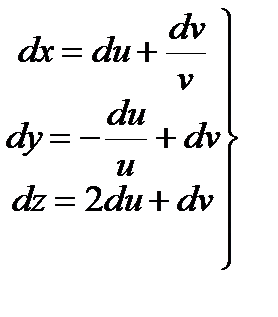                                           (6.11)

Отметим, что из условия задачи следует, что независимыми переменными мы должны считать x , y . Тогда функциями будут z , u , v . Таким образом, систему (6.11) следует решать относительно неизвестных du , dv , dz . В матричном виде это выглядит следующим образом

.

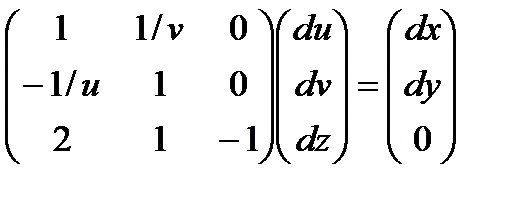Решим эту систему, используя правило Крамера. Определитель матрицы коэффициентов

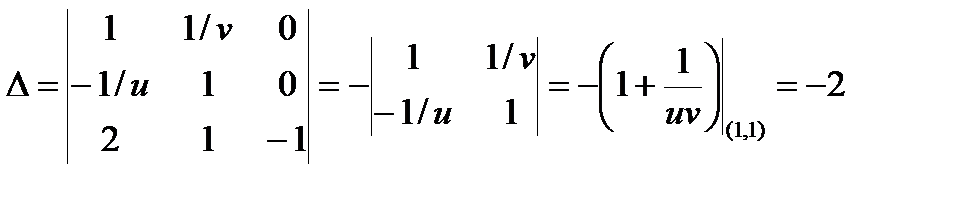, Третий «замещенный» определитель для dz  будет равен (его вычисляем разложением по последнему столбцу)

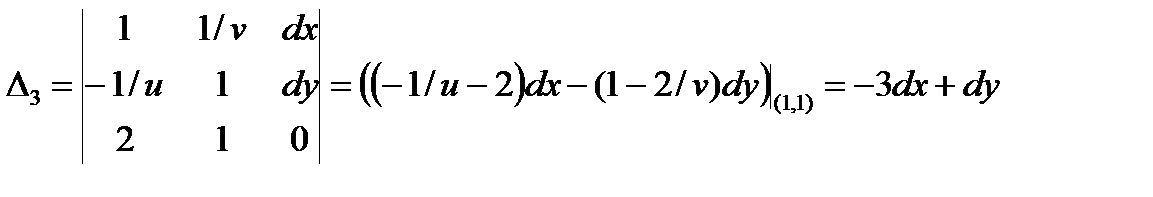, тогда

dz = 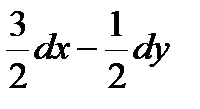, и , .

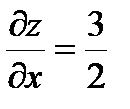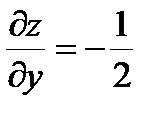Дифференцируем (6.11) еще раз (x , y – независимые переменные)

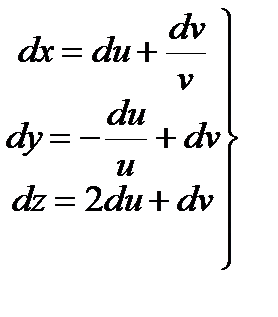
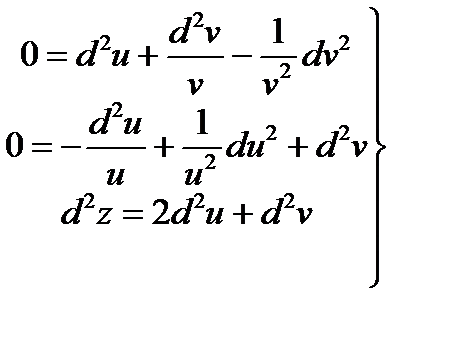
или

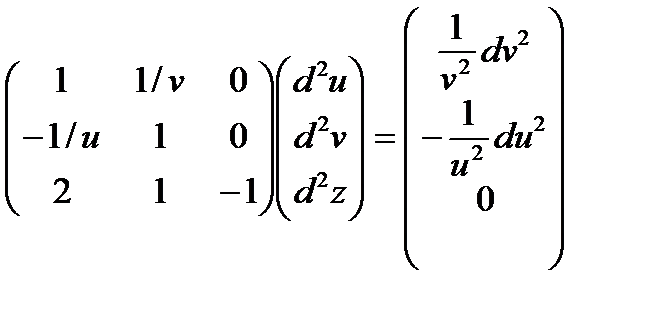
Матрица коэффициентов системы та же самая, третий определитель

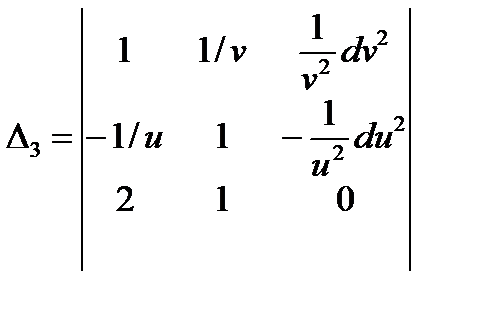
Решая эту систему, получим выражение для d ² z откуда можно будет найти нужную производную.

6.3. Дифференцируемые отображения

Производные отображения. Регулярные отображения. Необходимые и достаточные условия функциональной зависимости.