Пусть u = f(x) = f(x₁, x₂,…, x_n), где x_k – независимые переменные, так, что Dx_k = dx_k . Первый дифференциал функции

du = df = = .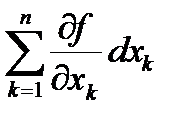

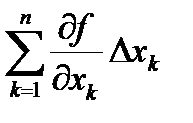Дифференциал в точке 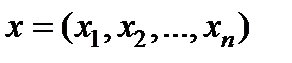рассматривается, как функция 2n независимых переменных

                                            .

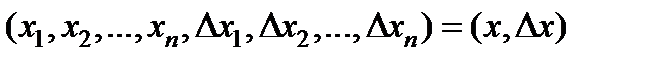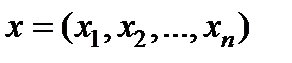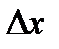Логически более естественно рассматривать , как точку, а  , как вектор. Вторым дифференциалом называется дифференциал от df , как функции точки x =(x₁, x₂,…, x_n). При этом точка (а лучше вектор) считается фиксированным. Кроме того, при втором дифференцировании приращения Dx_k  выбираются теми же самыми, что и при первом дифференцировании. Второй дифференциал обозначается d²u . Используя простейшие свойства дифференциала (x_k - независимое переменное) , получим

.

Последнее равенство можно было бы принять за определение второго дифференциала для случая независимых переменных.

Если сравнить последнее выражение с видом суммы, возведенной в квадрат

,

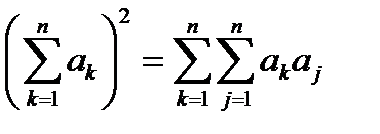то можно ввести некоторую удобную форму записи дифференциалов старших порядков. Определим символический дифференциальный оператор

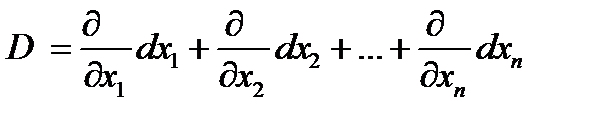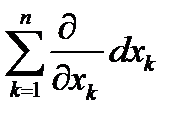= , Df = df

и правила действий с этим символическим оператором 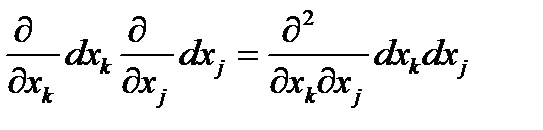. Согласно этим правилам D² = DD = 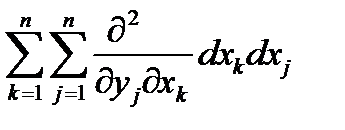. Точно также

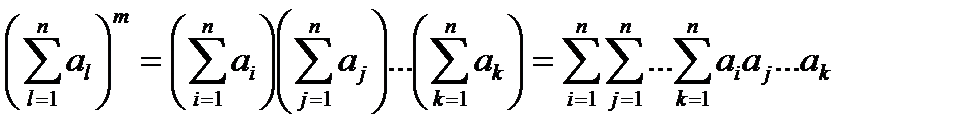
Отсюда для D^m = D(D^{m -1}) получается формула

D^m = .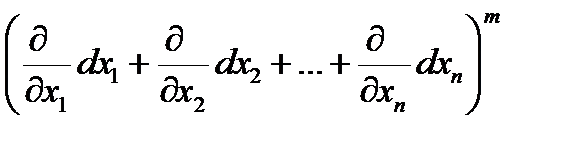

Таким образом, d²f = D²f , d^mf = D^mf .

Пример. u = f(x , y), D = 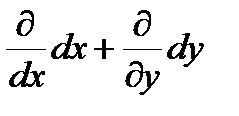. По формуле бинома

d^mf = D^mf = .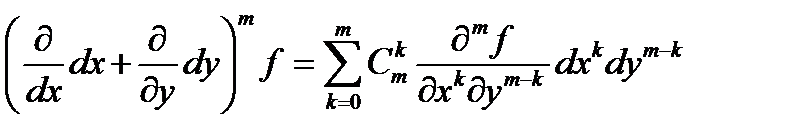

В общем случае

d^mf = D^m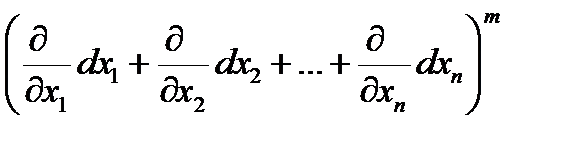f == f = = =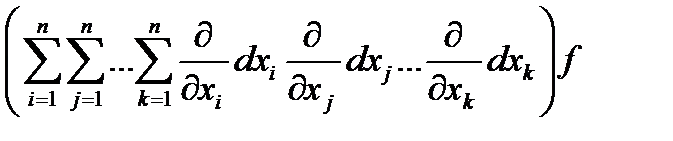

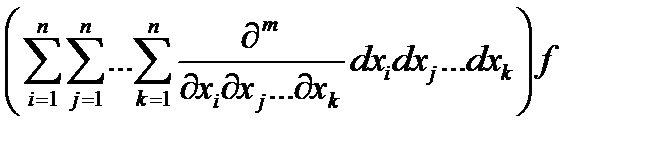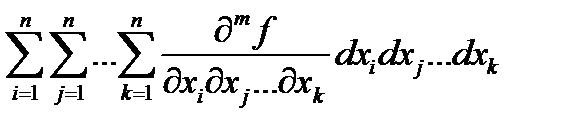
Определение. Через C^m ( G ) обозначают множество всех функций, определенных на открытом множестве G , имеющих там непрерывные частные производные до m –го порядка включительно.

Замечание. Дифференциалы высших порядков не обладают свойством инвариантности.

Пример. u = f(x , y), x = j(t₁,…, t_m), y = y(t₁,…, t_m), du = 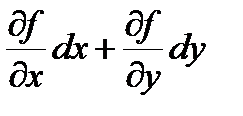, d²u = .

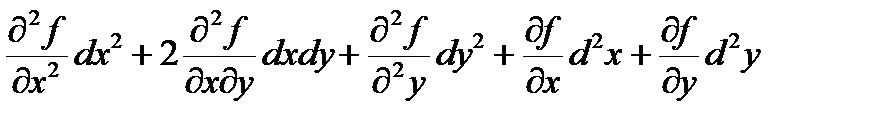Отметим, что в частном случае, когда внутренние функции суперпозиции являются линейными u = f(x₁, x_2,…, x_n), x_k = j_k(t₁,…, t_m)= a_k1t₁+…+ a_kmt_m , свойство инвариантности дифференциалов высших порядков будет выполняться, так как

d ²x_k=d ²j_k =0, …, d ^px_k = d ^pj_k = 0 .

Пример. Пусть u  = f(x)  (m +1) – раз дифференцируемая в некоторой окрестности U_r(x⁰) функция . Зафиксируем xΠU_r(x⁰) и положим x(t) = x⁰ + t  Dx  , F(t) = f(x(t)) . Тогда функция F(t) – (m +1) – раз дифференцируема в некоторой окрестности (-d , 1 + d ) интервала (0,1) (рис. 5.5)

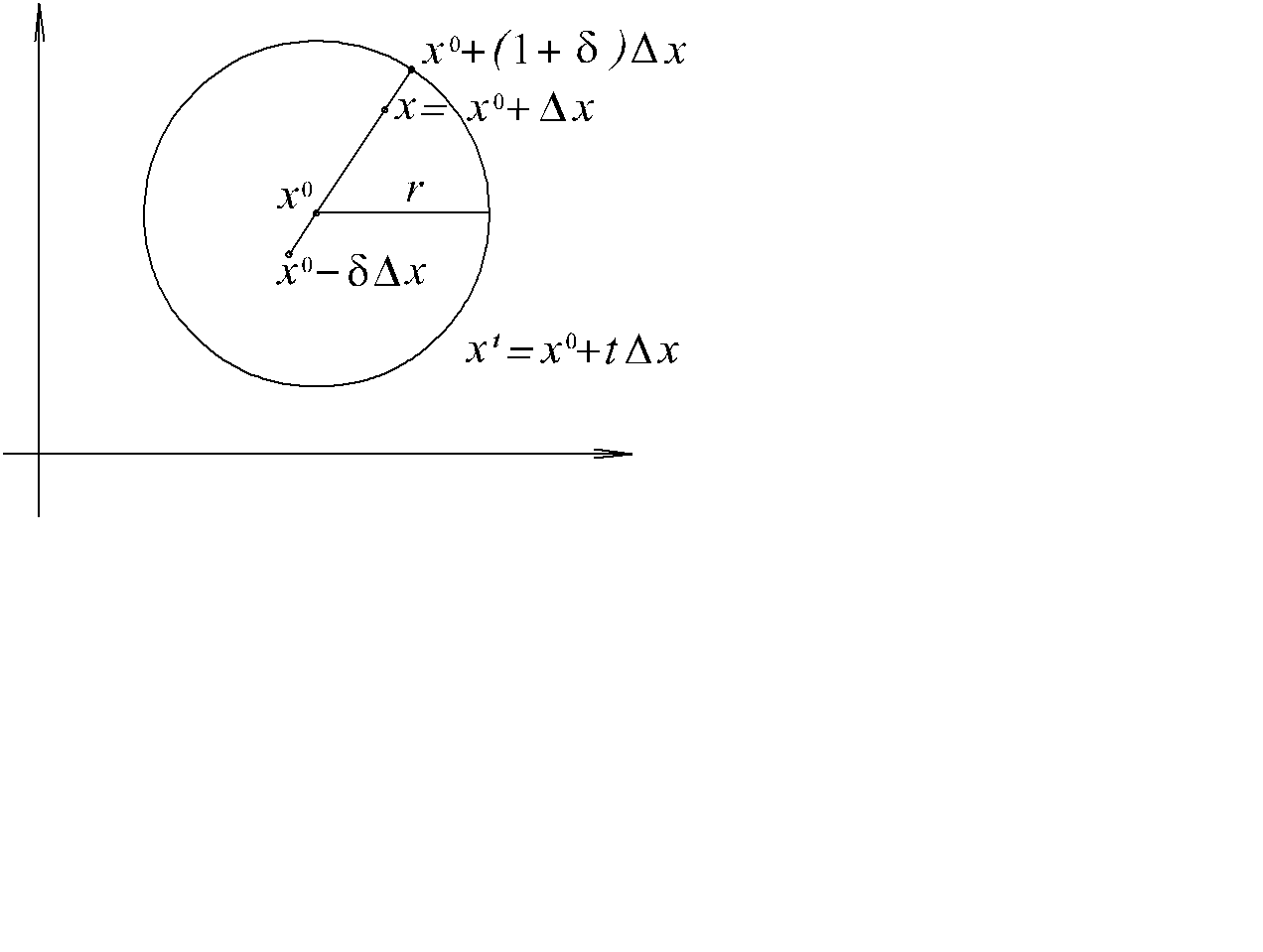
Рис. 5.5

и dF(t) = df(x), dF(0) = df(x⁰),…, d ^k F(t) = d ^k f(x) , d^kF(0) = d ^k f(x⁰), x = x(t) , x⁰= x(t) .

Действительно,

, ,…, .

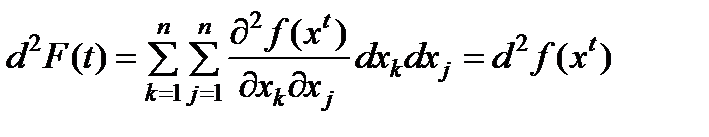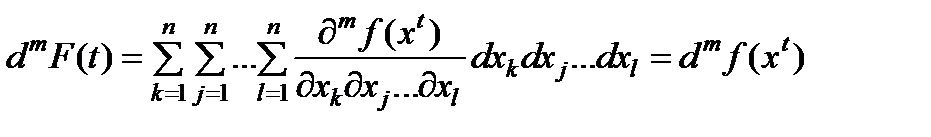5.3. Cвойство функций многих переменных

Теорема Лагранжа. Формула Тейлора.

5.3.1. Теорема Лагранжа для функций многих переменных

Определение . Область D называется выпуклой, если для любых двух точек x =(x₁,…, x_n), y =(y₁,…, y_n) из D , этой области будет принадлежать и отрезок их соединяющий, т.е. множество

[x , y]={zÎRⁿ : z = x + t (y – x), tÎ[0,1]}.

  Теорема. Если f(x) Î C¹(D), где D – выпукла, то " x⁰, x¹Î D $ x^q = x⁰ + q Dx , Dx= x¹ – x⁰, qÎ(0,1):

Df = f(x¹) – f(x⁰) = .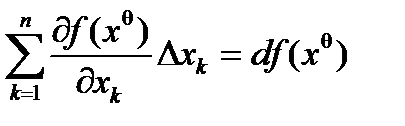

  Доказательство. Пусть x⁰, x¹Î D , x^t = x⁰ + t Dx , Dx = x¹ – x⁰ , F(t) = f(x^t) . Функция F(t) удовлетворяет условиям теоремы Лагранжа на [0,1]. Тогда

f(x¹) – f(x⁰) = F(1) – F(0) = F¢(q)= .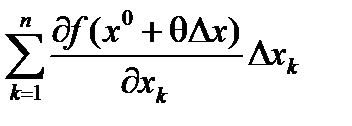

       Следствие. Если D выпукла, f Î C¹(D) и для " k " xÎD : 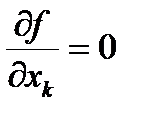, то f º const .

5.3.2. Формула Тейлора для функций многих переменных

Пусть u = f(x) определена на D , x⁰  - внутренняя точка D . Если  f  имеет в некоторой U(x⁰) производные (m +1)-го порядка, то в этой окрестности имеет место разложение

f(x) = ,                                (5.5)

где x^q = x⁰ + q Dx , Dx = x – x⁰ , qÎ(0, 1) .

Доказательство. Пусть x Î U(x⁰), x ^t = x⁰ + t Dx , F(t) = f(x⁰ + t Dx) . Функция F(t)  будет (m+1)- раз дифференцируема на некотором (-d, 1+d) (рис. 5.6).

Рис. 5.6

Кроме того, при линейной замене имеет место свойство инвариантности дифференциалов высших порядков  

dF(0) = df(x⁰),…, d^kF(0) = d ^k f(x⁰), d ^k F(q) = d ^k f(x^q) , x⁰= x(t⁰), x^q= x(t^q).

Равенство (5.5) будет следовать из разложения по формуле Тейлора функции F(t)

F ( t )=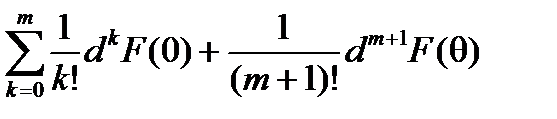

Теорема. Если f(x) имеет в окрестности точки x⁰ частные производные (m +1)-го порядка, непрерывные в самой точке x⁰ , то при x ® x⁰

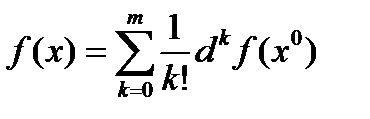+ o(r^m(x , x⁰))                           (5.6)

Доказательство (для случая n =2).  Как мы видели, в некоторой окрестности x⁰

f ( x ) = ,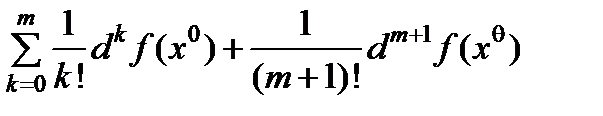

x^q = x⁰ + q Dx , Dx = x – x⁰ . Имеем

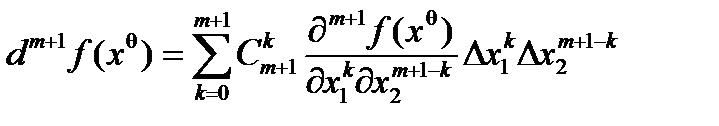, |Dx_k | £ r(x , x⁰). Откуда

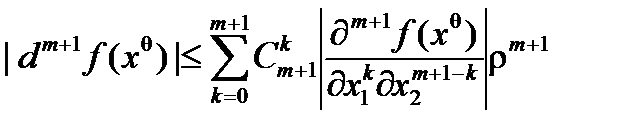£ Cr^{m +1}=o(r^m).

Замечание. Имеет место формула бинома Ньютона

.

Поэтому

d ^m f(x⁰) = 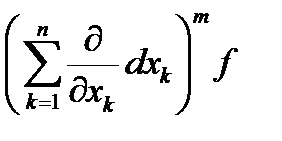=  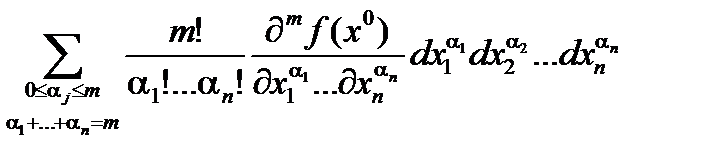       (5.7)

Подставляя (5.7) в (5.5) получим вид разложения по формуле Тейлора в развернутом виде

f ( x ) = 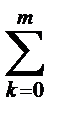+ o(r^m),                           (5.8)

Можно показать, что представление (5.8) в некотором смысле единственно. Именно, если при x ® x⁰ имеет место

f ( x ) = 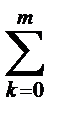+ o(r^m),

то коэффициенты a_a определяются единственным образом, а именно, имеют тоже выражение, что и в (5.8). В последней формуле использованы следующие обозначения: a - мульти-индекс, a=(a₁,…,a_n ), a_a = 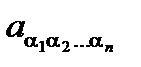 , |a|=a₁+…+a_n , a! = a₁!…a_n! , = , .

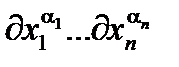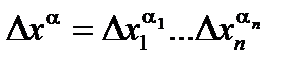Пример. Разложить в окрестности точки (1,1) функцию u = e^{x + y} до m -го порядка.

d ^ku = e^x+y(dx+dy)^k=e^x+y , e^x+y = 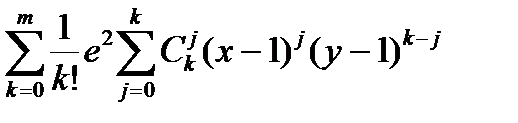+o(r^m).

Это же разложение можно получить из формулы e^v = .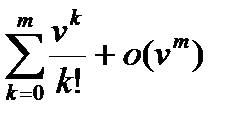

5.3.3. Экстремумы функций многих переменных. Необходимые условия экстремума

Пусть u = f(x) определена в окрестности точки x⁰ .

Локальный максимум в точке x⁰ : Для некоторой окрестности U(x⁰) выполнено

"x Î U(x⁰):f(x) £ f(x⁰).

Строгий локальный максимум в точке x⁰ : Для некоторой окрестности U(x⁰) выполнено

"xÎU(x⁰), x ¹ x⁰ : f(x) < f(x⁰).

Аналогично определяются минимумы. Локальным экстремумом называется локальный минимум или локальный максимум.

Теорема (необходимое условие экстремума). Пусть функция f(x) определена в окрестности точки x⁰ и имеет в этой точке частные производные первого порядка. Если x⁰ экстремум, то все частные производные равны нулю в этой точке.

Доказательство. Теорема Ферма по каждой переменной в отдельности.

Определение. Точка, в которой все частные производные первого порядка равны нулю, называется стационарной точкой функции.

Замечание 1. Стационарность точки x⁰ эквивалентна условию df(x⁰)=0.

Замечание 2. Глобальные максимумы или глобальные минимумы функции надо искать среди

1) стационарных точек,

2) точек, где не существуют частные производные первого порядка,

3) граничных точек.

Замечание 3. Равенство частных производных нулю не является достаточным для наличия экстремума.

Пример: z = xy , (0,0).