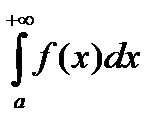Если | f(x)| £ g(x), xÎ[a ,+¥) (или xÎ[a , b]), то из сходимости интеграла  следует абсолютная сходимость интеграла . Из условной сходимости интеграла  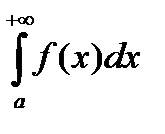следует расходимость интеграла .

3.2.2. Свойства несобственных интегралов. Интегрирование по частям

Простейшие свойства несобственных интегралов.

Если сходятся интегралы ,  , то будет сходиться и интеграл 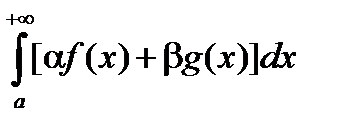 (a,b - константы), при этом

= + .

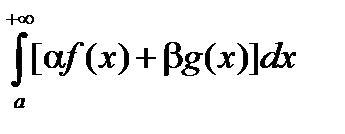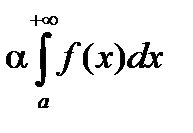Интегрирование по частям. Если u(x), v(x) непрерывно дифференцируемы на [a ,+¥) и существуют какие-либо два из трех выражений

, , ,

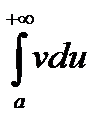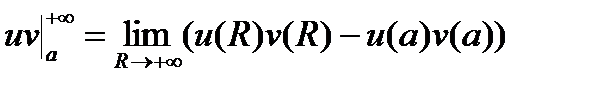то существует и третье и

= - .

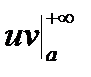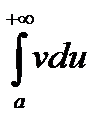Доказательство. Перейти к пределу при R®¥ в равенстве для собственных интегралов = - .

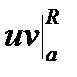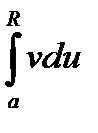Аналогичные свойства имеет место для несобственных интегралов второго рода.

Формула замены переменного

Пусть  f ( x ) непрерывна на [a , b) (b - число или символ +¥), j(t) – непрерывно-дифференцируема и строго монотонно возрастает на [a,b), a < b £ ¥, причем

a = j(a), 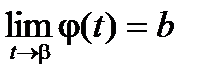, тогда

.

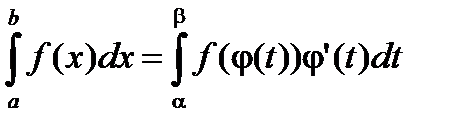Доказательство. В силу строгой монотонности функции j(t) для "RÎ [a , b)$ r : j(r)= R .

Отметим, что при будет и 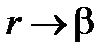(слайд «Суперпозиция»).

Суперпозиция

Далее следует перейти к пределу в равенстве

, (r®b, R ® b).

Замечание 1. В формуле замены переменной функция j может быть строго монотонно убывающей. Тогда в формулировке теоремы появятся соответствующие изменения j(b)= a , 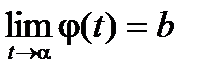, 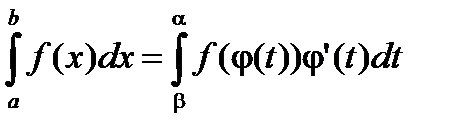(рис. 3.4).

Рис. 3.4

Замечание 2. Формула замены переменного справедлива и без условия монотонности функции j.

Например, пусть функция j  имеет три интервала монотонности (см. рис. 3.5)

Рис. 3.5

Тогда

, , .

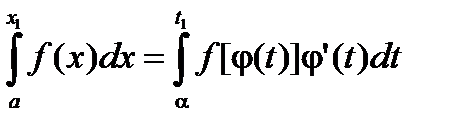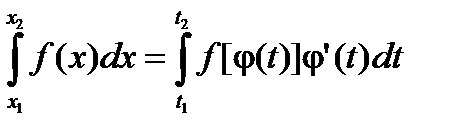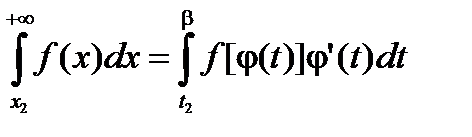Складывая эти равенства, получим ту же формулу замены переменного и для данного случая

.

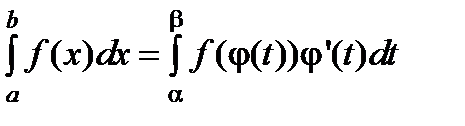Замечание 3. Несобственный интеграл 1-го  рода может быть подходящей заменой сведен к несобственному интегралу 2-го рода и наоборот.

Пример 1. .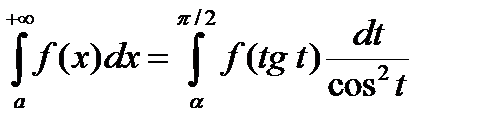

При некоторых заменах переменной вновь полученный интеграл может оказаться собственным (см. пример 2).

Пример 2.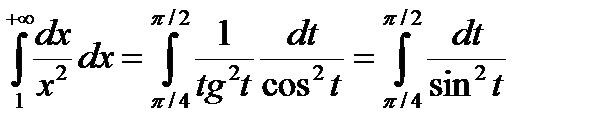

Рис. 3.6

Функции Эйлера

Гамма- функция Эйлера  G(p)= , определена при p > 0 .

Для доказательства сходимости интеграла  в области p > 0 отметим, что в окрестности 0 подинтегральная функция эквивалентна функции 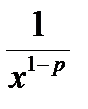, интеграл от которой сходится при условии 1- p < 1, то есть p > 0. В окрестности +¥ , подинтегральную функцию можно сравнивать с функцией  (имеющей сходящийся интеграл), именно, 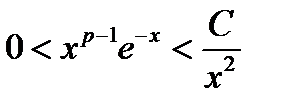 или 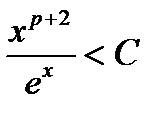. Существование константы C, для которой эти неравенства будут выполнены, следует из соотношений

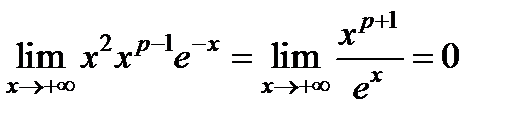, при p > 0.

Далее можно воспользоваться простейшим признаком сравнения.

Легко проверить, что G(1) = 1 (вычислить интеграл), G(p+1) = pG(p). Последнее равенство следует из формулы интегрирования по частям

G(p)= 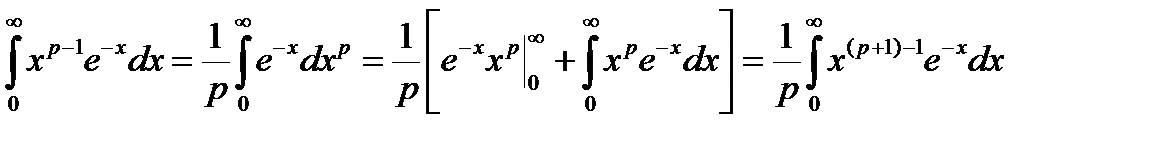= 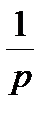G(p +1).

Бета-функция Эйлера определяется по формуле

B(p , q)= 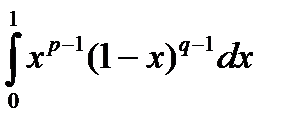,определена для p > 0, q > 0 .

Часть 4. n – мерное евклидово пространство

4.1. Основные определения

Метрические пространства, норма, скалярное произведение. Неравенство Коши-Буняковского. Сходимость.

Метрика. Расстояние

Рассмотрим всевозможные упорядоченные наборы из n - вещественных чисел

x = (x₁, x ₂ ,…, x_n).

Пользуясь геометрической терминологией,  x будем называть точкой, числа x₁, x₂,…, x_n  называются координатами точки. Для случаев n =1,2,3 мы имеем дело с точками на прямой, плоскости и в пространстве, соответственно.  Для двух точек x = (x₁, x₂,…, x_n), y = (y₁, y₂,…, y_n) величина

r(x , y)=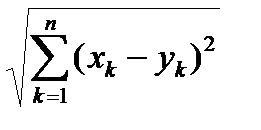

называется расстоянием между этими точками. Фундаментальными свойствами расстояния являются следующие три свойства.

1) " x,y :r(x,y) ³ 0, r(x,y) = 0 Û x = y

2) " x,y :r(x,y) = r(y,x)

3) " x , y , z :r(x , y) £ r(x , z) + r(z , y) (неравенство треугольника)

Первые два свойства очевидны, третье свойство будет доказано позже. Множество всевозможных точек x с расстоянием r(x , y), удовлетворяющим свойствам 1)-3) называется метрическим пространством. Обозначим это пространство Rⁿ .