Рассмотрим множество T Ì R^m и отображение j(t) из T в Rⁿ. Таким образом, для каждой точки t из T  однозначно сопоставлена точка x из Rⁿ. Это записывается в виде x =j(t) . Задание такого отображения равносильно заданию n  функций 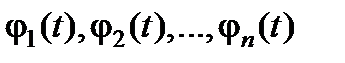, определенных на T, или в развернутом виде

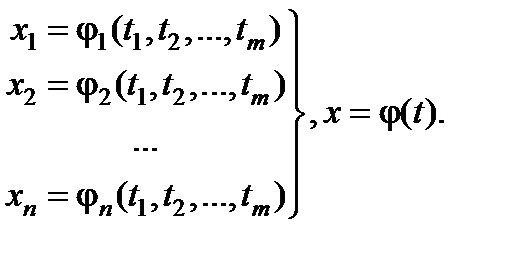
Отображение x =j(t) (его также можно называть функцией) называется непрерывным (например, в точке t⁰), если в этой точке непрерывны все «координаты» 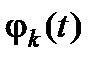этой функции. Так же, как и ранее, можно выписать неравенства, связывающие координаты с расстоянием

Эти неравенства позволяют дать эквивалентное определение непрерывности в терминах метрики евклидова пространства.

Функция x =j(t) называется непрерывной в точке t⁰ , если

"e > 0 $d>0: r(t , t⁰)<d Þ r(j(t), j( t⁰)) < e.

Определение сложной функции или суперпозиции. Пусть задано отображение x =j(t)  из T Ì R^m в множество X пространства Rⁿ и отображение u = f(x) из X в R .

u = f(x) , x Î X Ì Rⁿ, x = j(t), t Î T Ì R^m .

В результате последовательного выполнения этих двух отображений получим сложное отображение или функцию: u = f(j(t)), действующую из T в R .

Теорема (о непрерывности сложной функции). Пусть u = f(x) определена в некоторой a окрестности U_a(x⁰) точки x⁰ и непрерывна в этой точке, функция j(t) определена в некоторой окрестности U(t⁰), непрерывна в t⁰, причем x⁰= j(t⁰). Тогда в некоторой окрестности t⁰ существует сложная функция f(j(t)), непрерывная в точке t⁰.

Доказательство. Как уже ранее отмечалось, непрерывность функции j(t) в точке t⁰ означает, что

"e > 0 $d>0: r(t , t⁰)<d Þ r(j(t), j( t⁰)) < e .

Вначале докажем существование суперпозиции в некоторой окрестности точки t⁰. Пусть f(x) определена в U_a(x⁰), тогда для числа a $h>0: r(t , t⁰)< h Þ r(j(t), j(t⁰)) < a . Следовательно, в окрестности U_h(t⁰) будет определена суперпозиция f(j(t)). Докажем ее непрерывность. Пусть e> 0 для этого e

$d>0: r(x , x⁰)< d Þ | f(x) – f(x⁰)| < e .

В свою очередь, для d будет $ 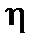>0: r(t , t⁰)<  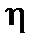Þ r(j(t), j(t⁰)) < d.

В итоге:  r(t , t⁰)< 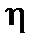 Þ  | f(j(t)) – f(j(t⁰))| < e ,  ч.т.д.

Следствие. Пусть f(x) непрерывна на открытом множестве D Ì Rⁿ и задана непрерывная кривая g : x=j(t),tÎ[a,b] , лежащая в D . Тогда сложная функция F(t)= f(j(t)) непрерывна на отрезке [a,b].

Замечание. Если для функции многих переменных зафиксировать все переменные кроме одного, то мы получим функцию одного переменного

F(x_k)=f( .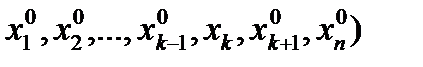

В этом случае можно говорить о непрерывности по одному переменному. Легко показать, что если функция непрерывна, то она будет непрерывной по каждому из переменных. Обратное утверждение не верно.

Определение. Множество DÌRⁿ называется связным, если любые его две точки можно соединить непрерывной кривой, целиком лежащей в D .

Теорема (о промежуточных значениях непрерывной функции на связном множестве). Пусть D открытое, связное множество и f(x) непрерывна на D , f(a)= A , f(b)= B , a , bÎD . Тогда для любого CÎ[A , B] существует cÎD такая, что f(c)= C (рис. 4.7).

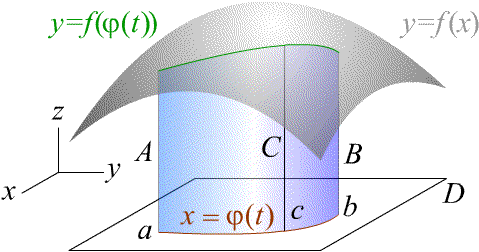
Рис. 4.7

Доказательство. По определению связного множества существует непрерывная кривая, лежащая в D , обозначим ее x = j(t), tÎ[a,b], такая, что j(a)=a, j(b)=b. По ранее доказанной теореме, суперпозиция F(t)= f(j(t)) представляет собой непрерывную на [a,b] функцию одного переменного. По теореме о промежуточных значениях непрерывной функции существует xÎ[a,b]: F(x)=C . Таким образом, точка c =j(x) будет искомой.

Терема 1 (Вейерштрасс). Непрерывная на компакте функция ограничена на этом компакте.

Доказательство. Предположим, что функция не ограничена на D. Тогда

" k$ x^kÎD :| f ( x^k )|> k                                                    (4.4) .

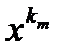Последовательность {x^k} – ограничена, так как D компакт, поэтому из нее по теореме Больцано-Вейерштрасса можно выбрать сходящуюся подпоследовательность { }® x⁰. Множество D замкнуто, поэтому точка x⁰Î D .  Из непрерывности функции следует, что f( )® f(x⁰), с другой стороны, согласно (4.4) , будет выполнено (| f( 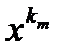)|> k_m) и f( 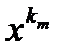)® ¥ . Полученное противоречие доказывает теорему.

Терема 2 (Вейерштрасс). Непрерывная на компакте функция достигает своих точных граней.

Доказательство. Докажем для верхней грани. Из определения M =sup f(x) для

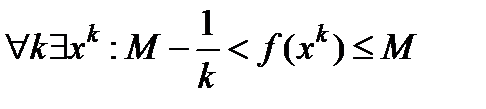                                                                                             (4.5)

Последовательность {x^k} – ограничена, так как D компакт, поэтому из нее по теореме Больцано-Вейерштрасса можно выделить сходящуюся подпоследовательность { }® x⁰. Из замкнутости D следует, что точка x⁰Î D .  Из непрерывности функции следует, что f( 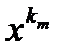)® f(x⁰). Согласно (4.5) будет выполнено неравенство  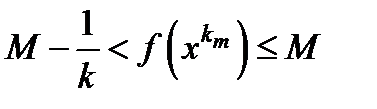, поэтому f( 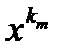)® M  и , таким образом, f(x⁰) = M  ч.т.д..

4.3.4. Равномерная непрерывность функции многих переменных. Терема Кантора

Определение. Функция f(x) называется равномерно непрерывной на множестве D , если выполнено условие Коши:

" e > 0 $ d > 0 " x¢, x¢¢Î D , r( x¢, x¢¢) < d : | f(x¢¢) – f(x¢)| < e .

Замечание. Если функция равномерно непрерывна на множестве D , то она непрерывна на этом множестве.

Теорема (Кантор). Непрерывная на компакте D функция равномерно непрерывна на D .

Доказательство. От противного.

$ e₀ > 0 " d > 0 $ x , y Î D , r( x , y ) < d : | f(x) – f(y)| ³ e₀ .

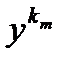В качестве d  будем брать последовательность 1/k .  В результате получим две последовательности {x^k}, {y^k} таких, что r( x^k,y^k ) < 1/k : |f(x^k) – f(y^k)| ³ e₀ . Последовательность {x^k} – ограничена, так как D компакт, поэтому из нее по теореме Больцано-Вейерштрасса можно выбрать сходящуюся подпоследовательность { }® x⁰. Из условия r( , ) < 1/k_m  следует, что последовательность { 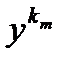}® x⁰ . Действительно,  r( x⁰, 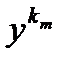)£ r( x⁰, )+ r( , 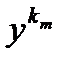) (неравенство треугольника). Из непрерывности функции следует, что f( 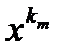)® f(x⁰) , f( 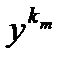)® f(y⁰) , откуда следует | f( 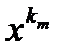) - f( )|® 0 , что противоречит неравенству | f( 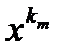) – f( )| ³ e₀ .

Часть 5. Дифференцируемые функции многих переменных

5.1. Дифференцируемость, частные производные функции многих переменных

Частная производная. Дифференциал. Производная по заданному направлению, градиент.