См. слайд «Частная производнная».
Частная производная
Некоторые обозначения 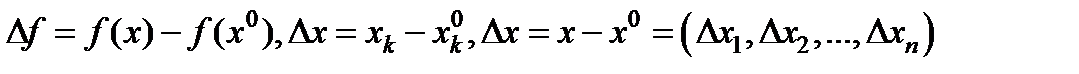 .
.
Определение. Функция f(x) дифференцируема в точке в точке x0 , если ее приращение в этой точке представимо в виде
Df = (A, Dx)+o(r),
где (A,Dx)= 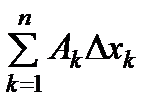 , r=r(x,x0), o(r)=e(x, x0)r(x,x0),
, r=r(x,x0), o(r)=e(x, x0)r(x,x0), 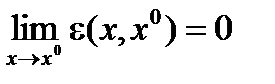 .
.
Линейная функция (A ,Dx) называется дифференциалом и обозначается
df(x0) =(A,Dx)= A1Dx1 +…+ AnDxn .
Замечание. В определении дифференциала величину o(r)=er можно записывать в виде
a1Dx1+a2Dx2+…+anDxn =(a , Dx), где a - бесконечно малый вектор.
Действительно, имеем er= 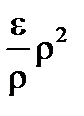 =
= 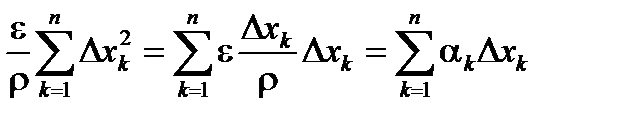 , и обратно,
, и обратно, 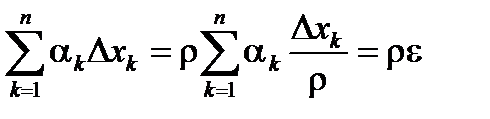 .
.
Теорема (необходимое условие дифференцируемости). Всякая дифференцируемая в точке x0 функция непрерывна в этой точке.
Утверждение следует непосредственно из определения дифференцируемости.
Теорема. Если f(x) дифференцируема в точке x0 и df = 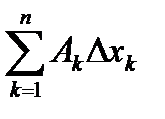 , то в этой точке существуют все частные производные
, то в этой точке существуют все частные производные 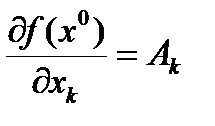 .
.
Утверждение следует непосредственно из определения дифференцируемости.
Следствие. Дифференциал функции в точке (коэффициенты Ak ) определяется однозначно.
Теорема (достаточные условия дифференцируемости). Если функция f имеет частные производные в некоторой окрестности точки M0 , непрерывные в самой точке, то функция f дифференцируема в этой точке.
Доказательство (для случая n = 2). Для приращения функции можно записать равенства
Df = f(x,y) – f(x0,y) + f(x0,y) – f(x0,y0)= 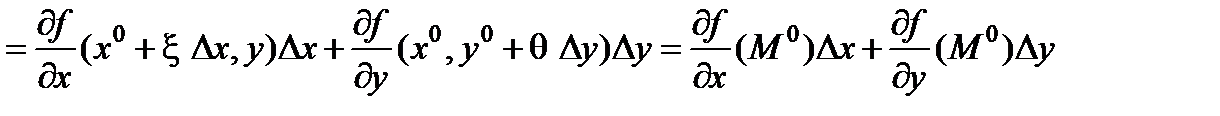 +
+ 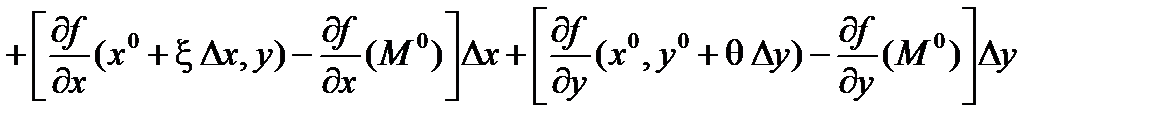 =
=
= 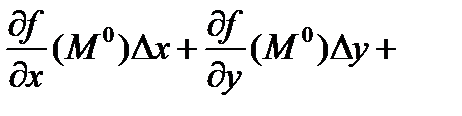 +aDx +bDy ,
+aDx +bDy ,
где a , b - бесконечно малые функции. Здесь была использована теорема Лагранжа о конечных приращениях.
Пример функции, имеющей частные производные в точке, но не дифференцируемой в точке f ( x , y ) = 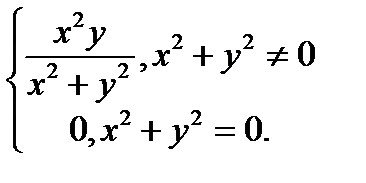 (слайд «Сечения»).
(слайд «Сечения»).
Сечения
Отметим, что | f ( x , y )| £ | y | Þ функция f(x , y) непрерывна всюду. Обе производные в точке 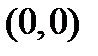 равны нулю:
равны нулю: 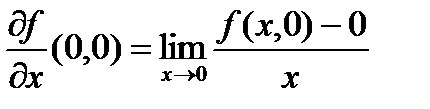 =
= 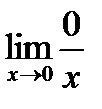 =0,
=0, 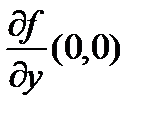 =
= 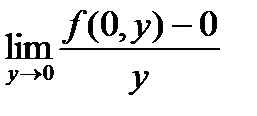 =
= 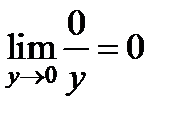 . Если бы функция была дифференцируема в точке
. Если бы функция была дифференцируема в точке  , то Df = o(r) Þ
, то Df = o(r) Þ 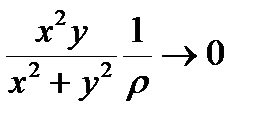 , или
, или 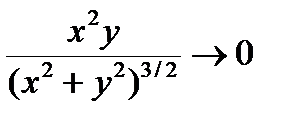 . Но при x = y получим
. Но при x = y получим 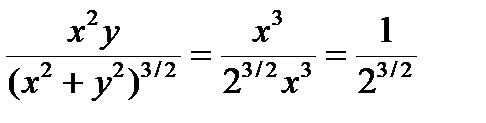 .
.
5.1.3. Простейшие свойства дифференциала. Дифференцирование сложной функции
Теорема. Пусть u = f(x) дифференцируема в точке x0 = (x10, x20,…, xn0) и функция j(t), t =(t1,…, tm) дифференцируема в точке t0 и x0 = j(t0). Тогда в окрестности точки t0 определена сложная функция F(t) = f(j(t)) и эта функция дифференцируема в точке t0 и
dF = 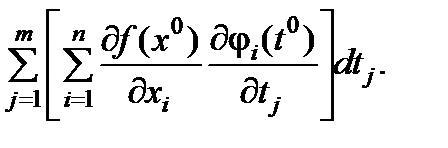
Доказательство. В силу дифференцируемости f и jj эти функции непрерывны в точках x0 и t0 соответственно. Из теоремы о непрерывности сложной функции суперпозиция определена в некоторой окрестности точки t0 . Для краткости, будем обозначать r=r(x , x0)=r(j(t),j(t0)), 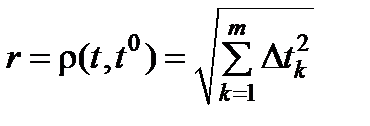 , Dxi =ji(t) – ji(t0) . Отметим, что
, Dxi =ji(t) – ji(t0) . Отметим, что 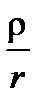 ограничено в некоторой окрестности точки t0 . Действительно,
ограничено в некоторой окрестности точки t0 . Действительно,
r £ 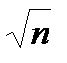 max|Dxi |, |Dxi | =
max|Dxi |, |Dxi | = 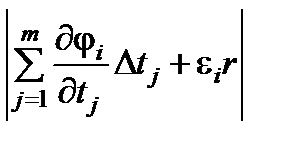 £
£ 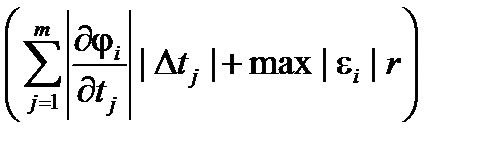
Так как 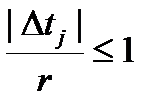 , то
, то 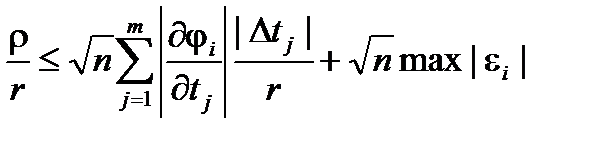 , откуда и следует ограниченность этой функции. Далее
, откуда и следует ограниченность этой функции. Далее
DF =Df = 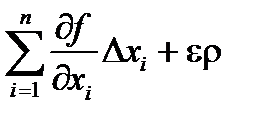 , Dxi =
, Dxi = 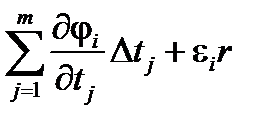 .
.
Подставляя выражения Dxi из второго равенства в первое получим
DF = 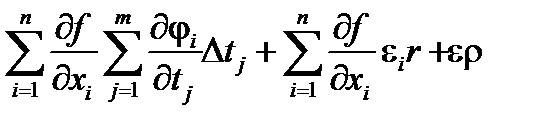 =
= 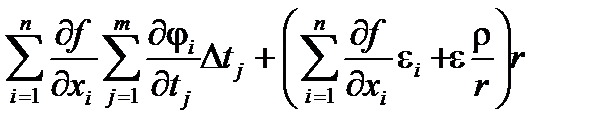 .
.
Из ограниченности 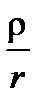 следует, что e¢ =
следует, что e¢ = 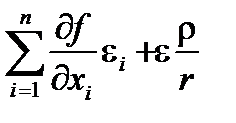 - бесконечно малая функция и дифференцируемость сложной функции доказана. При этом дифференциал равен
- бесконечно малая функция и дифференцируемость сложной функции доказана. При этом дифференциал равен
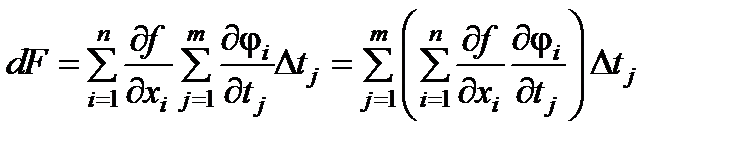
Следствие. В силу единственности дифференциала, справедливо равенство
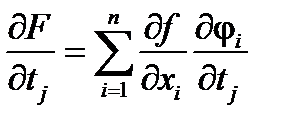 .
.
5.1.4. Инвариантность формы первого дифференциала
Пусть F(t) = f(j(t)), t Î Rm сложная функция, как уже отмечалось
dF = 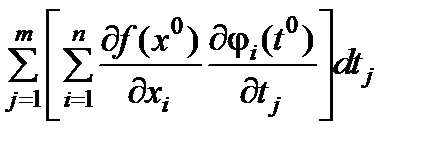 =
= 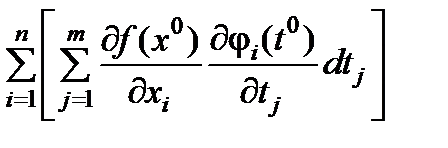 =
= 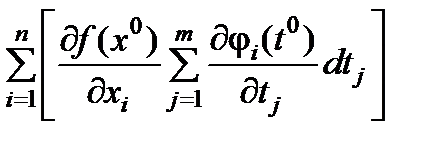 =
= 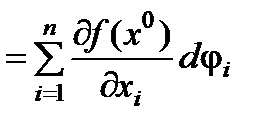 =
= 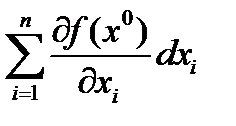 .
.
Таким образом,
dF = 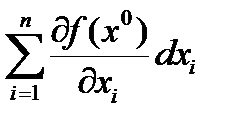 .
.
Первый дифференциал функции F имеет такую же форму, как и в случае, когда x является независимым переменным. Это свойство носит название свойством инвариантности формы первого дифференциала. В частности, отсюда следуют широко используемые свойства дифференциала
1) d(u+v) = du + dv.
2) d(uv) = vdu + udv .
3) d(u/v) = (vdu – udv)/v2.
Докажем третье свойство.
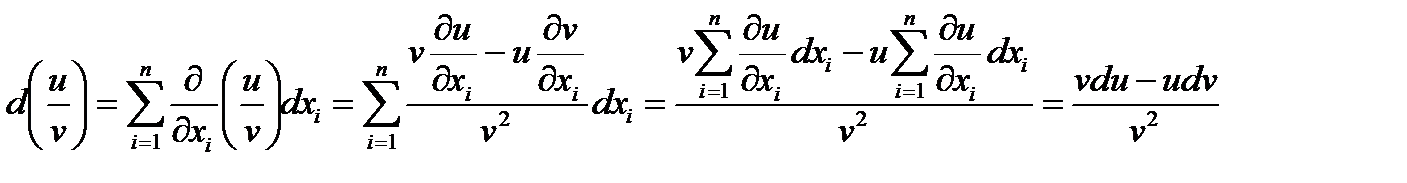 , ч.т.д.
, ч.т.д.
5.1.5. Производная по заданному направлению. Градиент
Пусть u = f(x , y , z) , M0(x0, y0, z0)Î D . Градиент функции f в точке M0 определяется по формуле grad f = 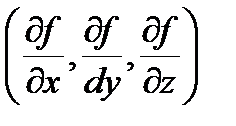 =
= 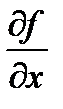 i +
i + 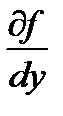 j +
j + 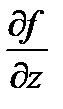 k .
k .
Пусть l единичный вектор ||l ||=1, l = cos a i + cos b j + cos g k , обозначим текущую точку на луче, выходящем из исходной точки в направлении вектора l , через
M t = (x0 + t cos a , y0 + t cos b , z0 + t cos g )=M0 + t l .
Производной функции f(x , y , z) в точке M0 по направлению вектора l называется предел
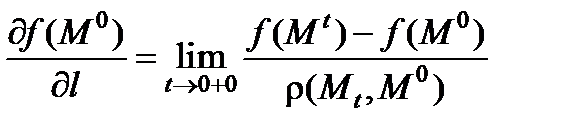 .
.
Для иллюстрации рассмотрим функцию двух переменных 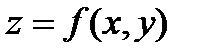 . Точка
. Точка 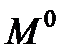 и текущая точка
и текущая точка 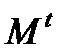 , лежащая на луче
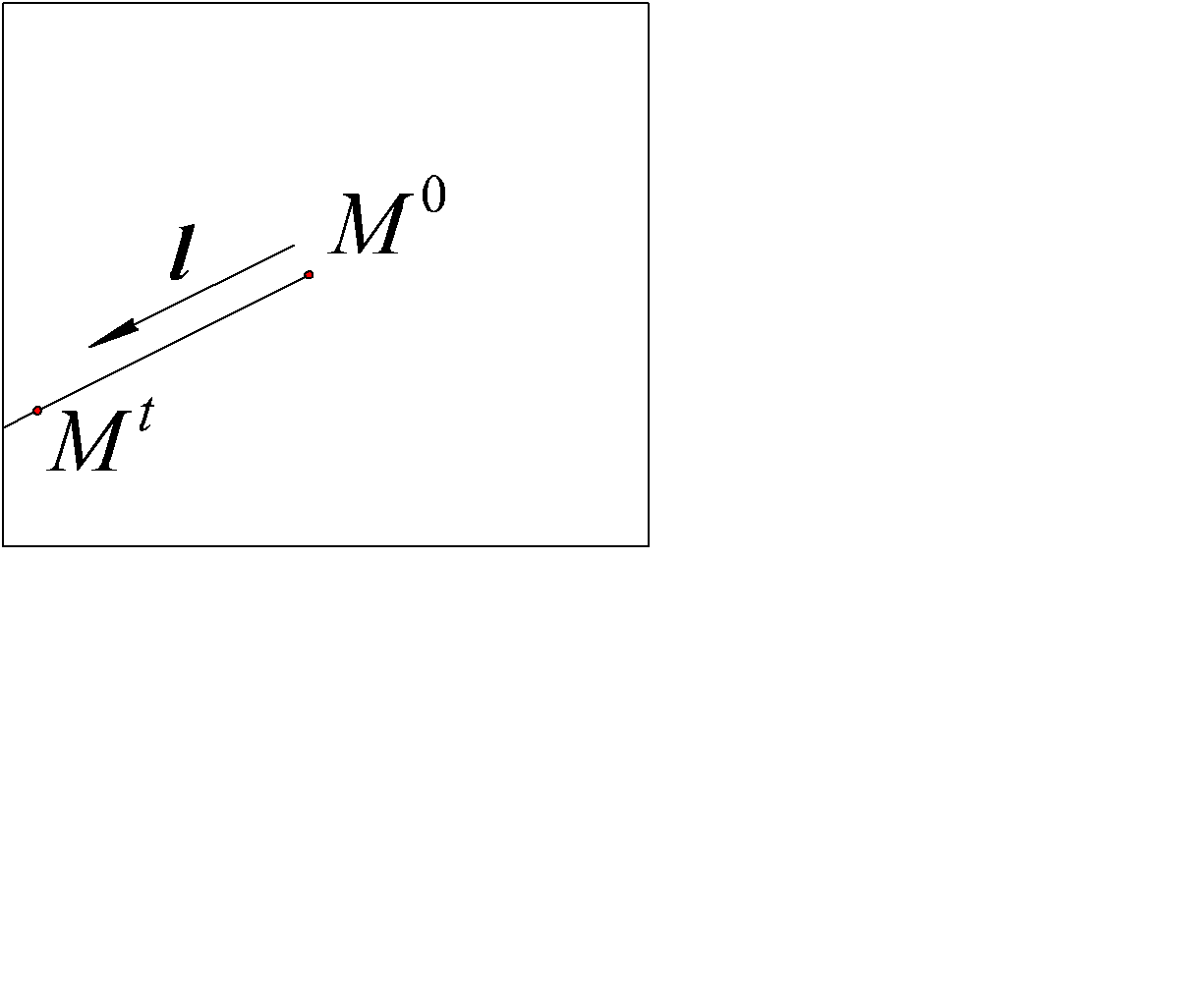
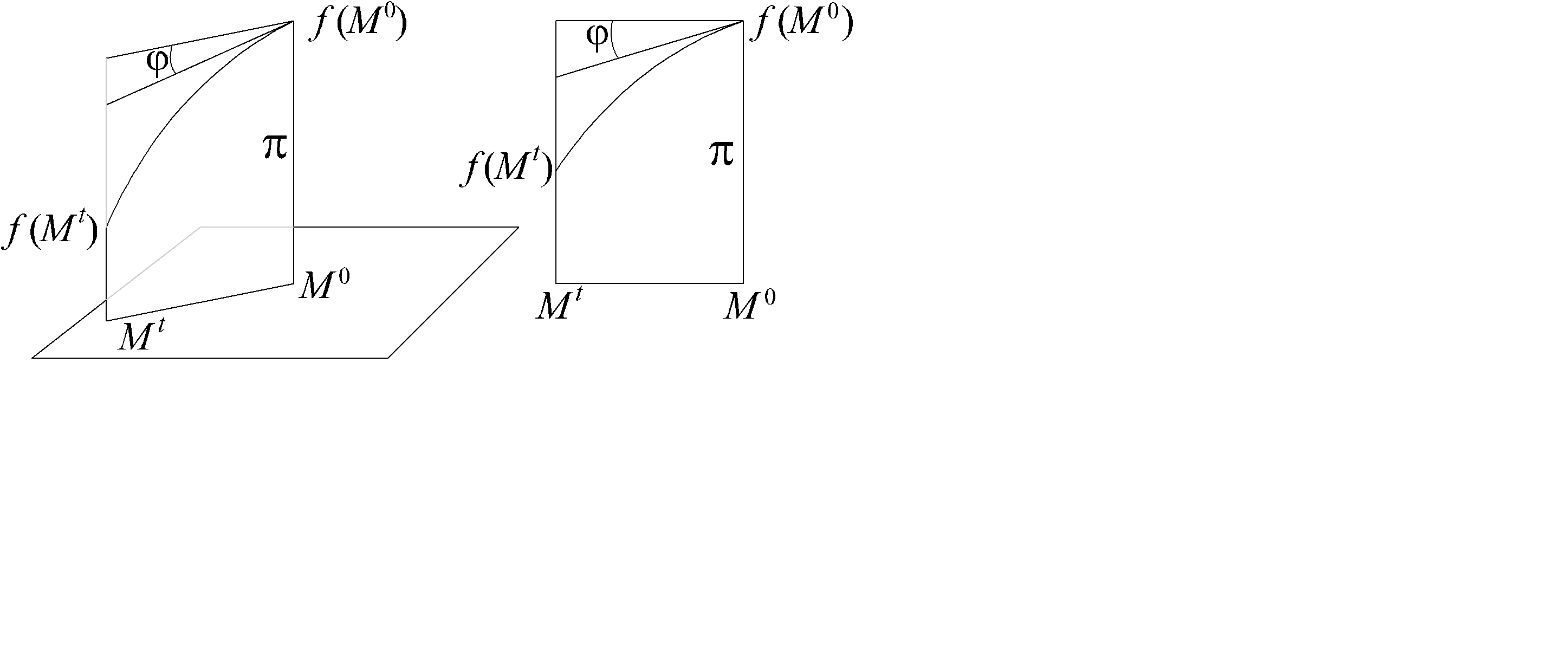
, лежащая на луче 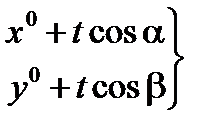 показаны на рис. 5.1. В плоскости
показаны на рис. 5.1. В плоскости  (рис. 5.2) предел
(рис. 5.2) предел 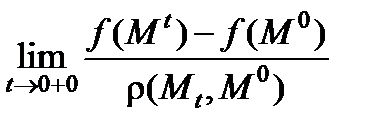 представляет собой обычную производную функции, которая получается в сечении поверхности
представляет собой обычную производную функции, которая получается в сечении поверхности  плоскотью проходящей через точку M0 параллельно вектору l = cos a i + cos b j и оси Oz.
плоскотью проходящей через точку M0 параллельно вектору l = cos a i + cos b j и оси Oz.
| 
|
| Рис. 5 .1 | Рис. 5.2 |
Теорема. Если функция f дифференцируема в точке M0 , то
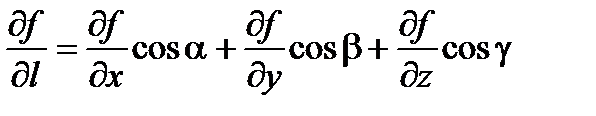 =(grad f , l )
=(grad f , l ) 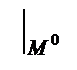
Доказательство. 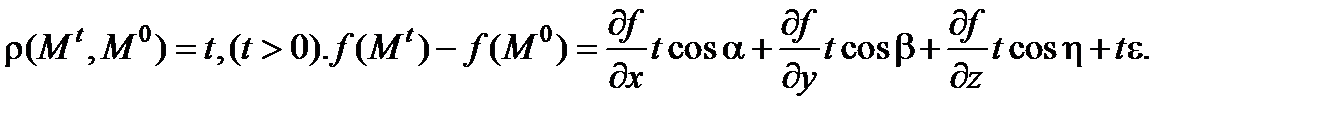 Отсюда, по определению производной по направлению получается требуемое неравенство
Отсюда, по определению производной по направлению получается требуемое неравенство
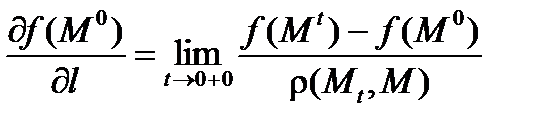 =
= 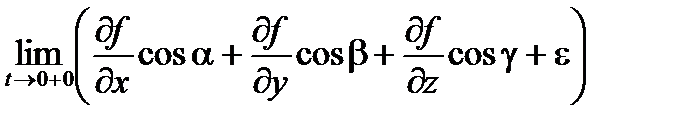 =(grad f , l ).
=(grad f , l ).
Из последнего неравенства следует, что у дифференцируемой функции существует производная по любому направлению.
Задача. Для заданной функции f(x) в точке x0 найти направление, в направлении которого функция f(x) имеет максимальный рост (максимальное убывание).
Решение. Так как 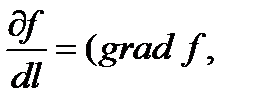 l) то искомое направление определяется вектором l =
l) то искомое направление определяется вектором l = 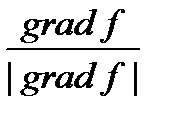 .
.
5.2. Гладкие поверхности
Касательная и нормаль к поверхности. Способы задания поверхностей. Частные производные высших порядков. Дифференциалы высших порядков.
Дата: 2019-03-05, просмотров: 369.