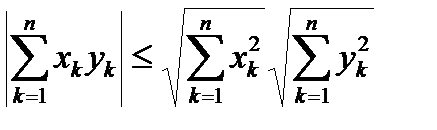.

В пространстве Rⁿ введем операции сложения между элементами этого множества и операцию умножения на вещественные числа по правилам:

x + y =(x₁+ y₁,x₂+ y₂,…,x_n+ y_n), l x = (lx₁, lx₂,…, lx_n),

где x = (x₁,x₂,…,x_n), y = (y₁,y₂,…,y_n).

В двухмерном и трехмерном пространстве эти операции интерпретируются, как операциями над радиус-векторами, соответствующих точек.

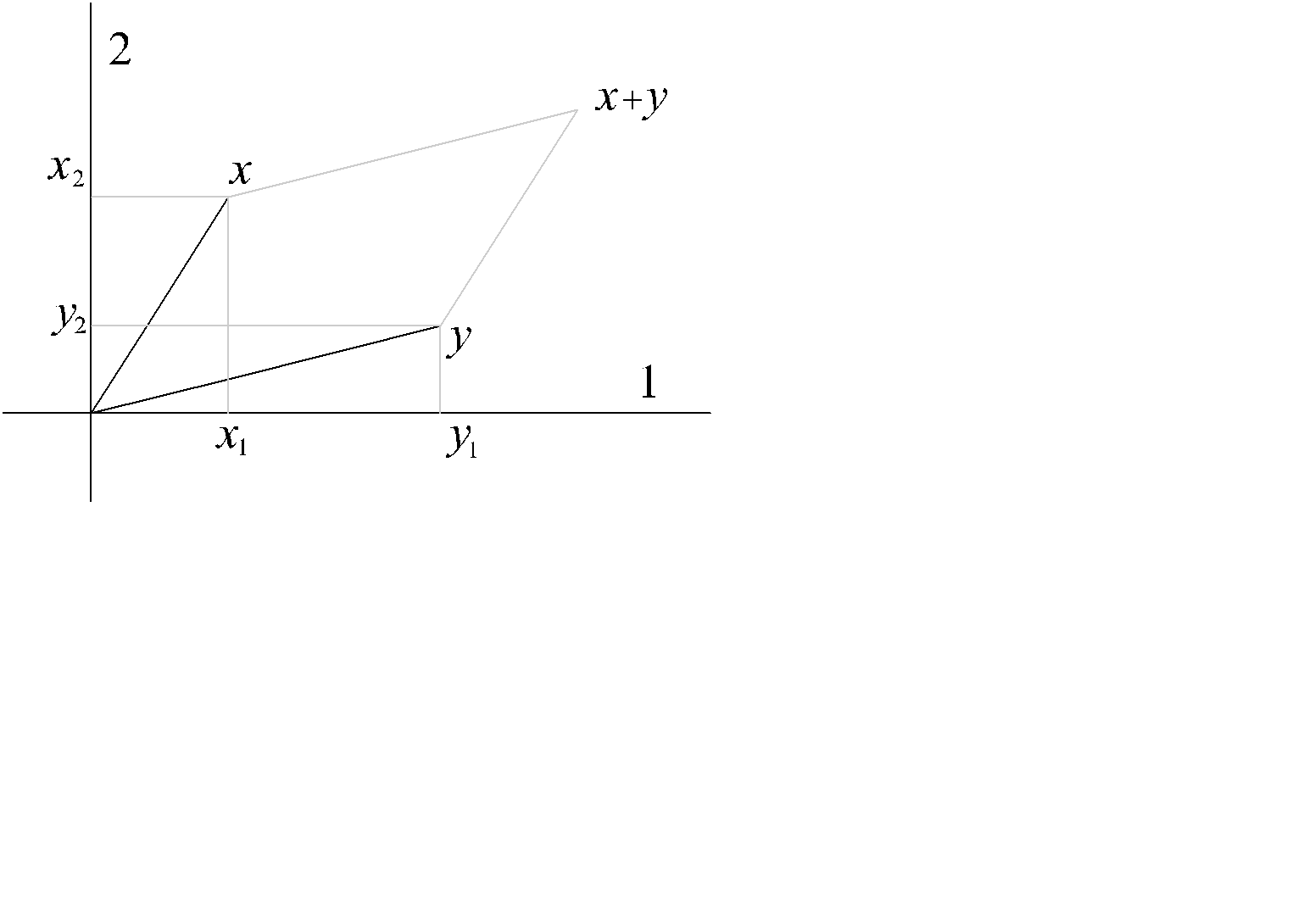
Рис. 4 . 1

1) Величина 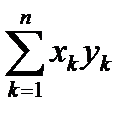 - называется скалярным произведением и обозначается (x , y). Величина  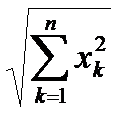называется нормой и обозначается || x ||.

В терминах нормы неравенство Коши-Буняковского можно записать в виде

|(x , y)| £ || x || || y ||.

Доказательство неравенства Коши-Буняковского.

0 £ || x +ly ||²= 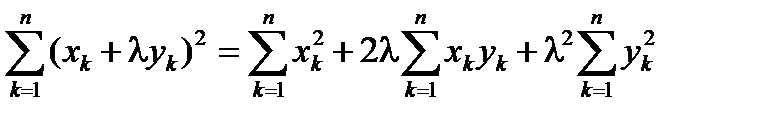=|| x ||²+2l(x , y)+l²|| y ||²= al²+2lb + c .

Так как это неравенство (al²+2lb + c ³ 0) справедливо для всех l , то для дискриминанта квадратного трехчлена al²+2lb + c  будет выполнено неравенство b² – ac £ 0, или (x , y)²£ || y ||² || x ||², откуда и следует требуемое утверждение.

Теорема. Для нормы справедливо неравенство || x + y || £ || x || + || y ||.

Доказательство.

|| x + y ||²= 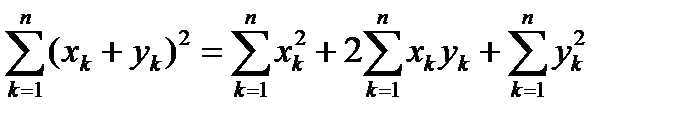£|| x ||²+2 || x || || y ||+ || y ||² =(|| x ||+|| y ||)².

Фундаментальные свойства нормы.

1) || x ||³0, || x ||=0 Û x=q , (q= (0,0,…,0)),

2) ||lx|| = |l| ||x|| ,

3) || x + y || £ || x ||+|| y ||.

Фундаментальные свойства скалярного произведения.

1) (x , x)³0, (x , x)=0Û x=q , (q= (0,0,…,0))

2) (x,y)=(y,x)

3) (lx,y)=l(x,y)

4) (x+y,z)=(x,z)+(y,z).

Определение. Пространство Rⁿ со скалярным произведением (x , y) называется евклидовым пространством.

Отметим, что между введенными понятиями, расстоянием, нормой и скалярным произведением имеются следующие равенства: r(x , y)=|| x - y ||, (x , x)=|| x ||².

Доказательство неравенства треугольника для расстояния.

r(x , y)=|| x - y ||=|| x – z + z - y ||£|| x - z ||+|| z - y ||=r(x , z)+ r(z , y).

4.1.3. Геометрическая терминология в Rⁿ

(n – мерный) открытый шар радиуса e c центром в точке x₀ или e окрестность точки x₀:

U_e(x₀)={ xÎRⁿ:r(x , x₀)<e }.

(n – мерный) замкнутый шар радиуса e c центром в точке x₀ :

_e(x₀)={ xÎRⁿ:r(x , x₀)£e }.

(n – мерная) сфера радиуса e c центром в точке x₀ :

S_e(x₀)={ xÎRⁿ:r(x , x₀)= e }.

В пространстве Rⁿ(n >1) под окрестностью ¥ понимается любое множество вида {xÎRⁿ:r(x , x⁰)>r}, для произвольного числа r , и произвольной точки x⁰.

( n – мерный) параллелепипед : B =[a₁, b₁]´ [a₂, b₂]´…´ [a_n , b_n].

Пример. Одномерная проекция (на R¹) двухмерного параллелепипеда (квадрата) (рис. 4.2).

Рис. 4.2

Двухмерная проекция (на R²) трехмерного параллелепипеда (куба) (рис. 4.3).

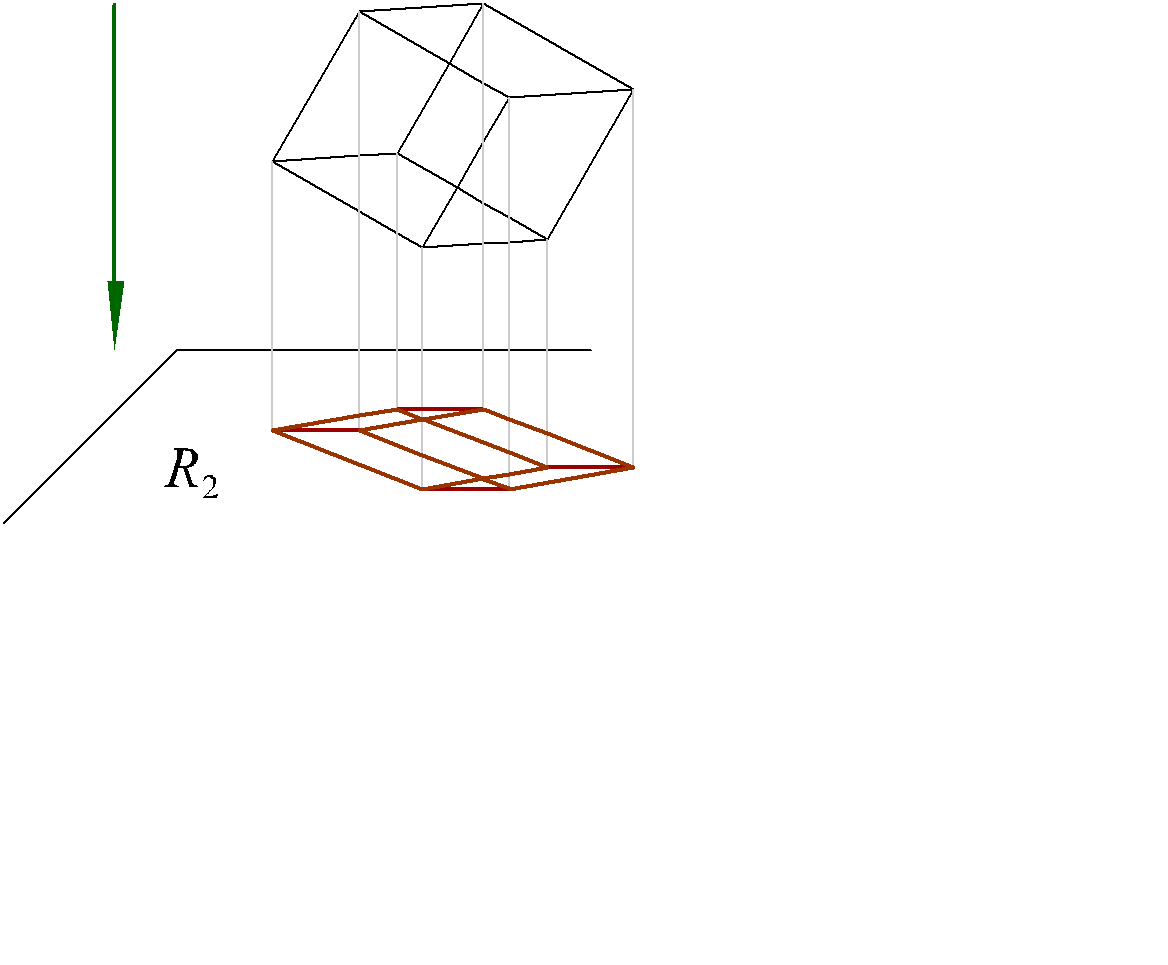
Рис. 4.3

Трехмерная проекция (на R³) четырехмерного параллелепипеда (четырехмерного куба) (рис. 4.4, слайд «Куб 4»).

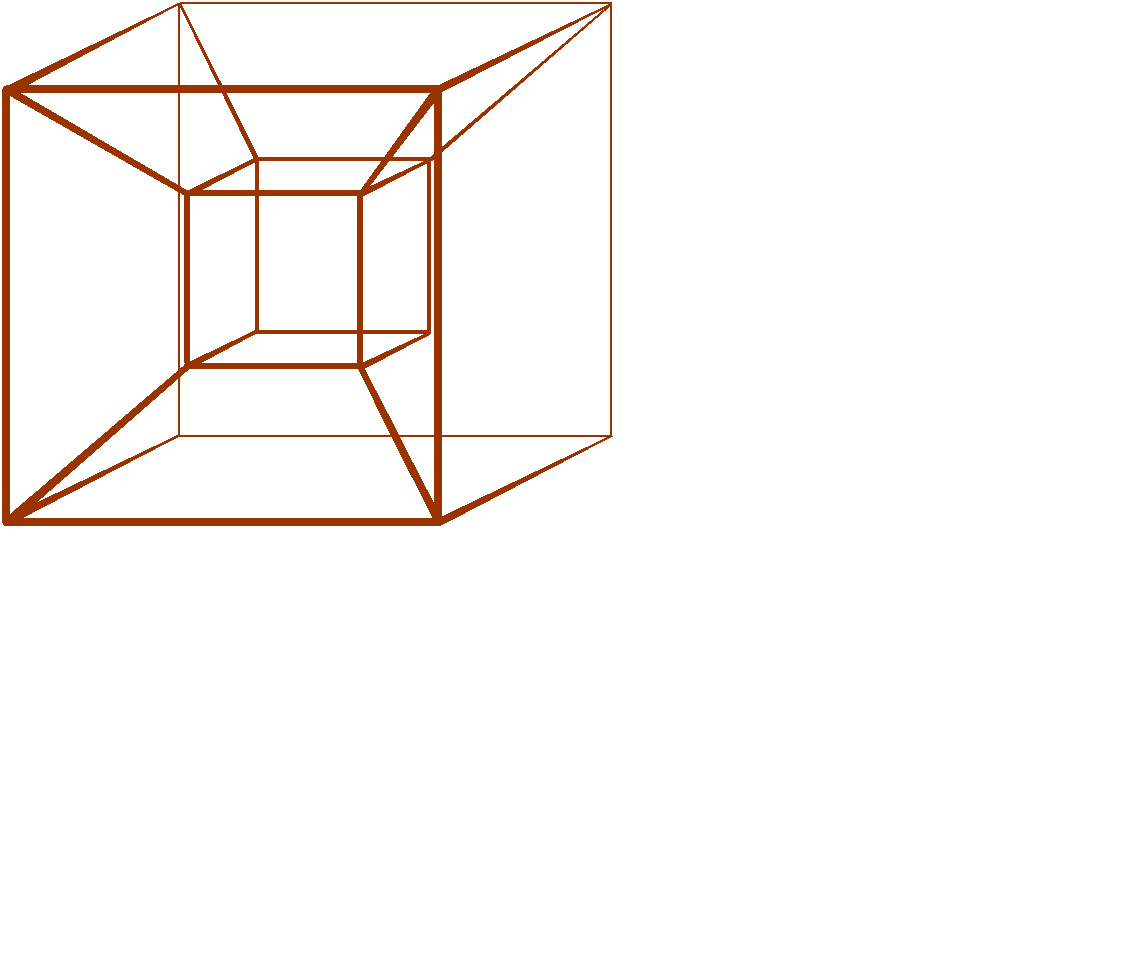
Рис. 4.4

Куб 4

В этом случае эту проекцию надо себе представлять в виде скелета из ребер в нашем трехмерном пространстве. На рисунке же изображена плоская картинка, то есть еще одна проекция этой трехмерной проекции на плоскость рисунка (двойная проекция: из R⁴ в R³, затем из R³ в R².

Проколотая окрестность точки: 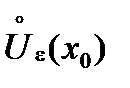={ xÎRⁿ:0<r(x , x₀)<e }.

Внутренняя точка множества – точка, которая принадлежит множеству вместе с некоторой своей окрестностью.

Открытое множество – множество, все точки которого внутренние.

Предельная точка множества – точка, в любой окрестности которой содержится хотя бы одна точка множества, отличная от нее самой (или, что тоже, в любой окрестности этой точки содержится бесконечно много точек из данного множества).

Замкнутое множество – множество, содержащее все свои предельные точки.

Пример. Для _e(x₀) множество внутренних точек совпадает с U_e(x₀). _e(x₀) – замкнутое множество. U_e(x₀) – открытое множество.

Замыкание множества – само множество плюс все его предельные точки. Обозначается чертой сверху.

Ограниченное множество – множество, содержащееся в некотором шаре.

Пример. Ограниченная последовательность (рис. 4.5)

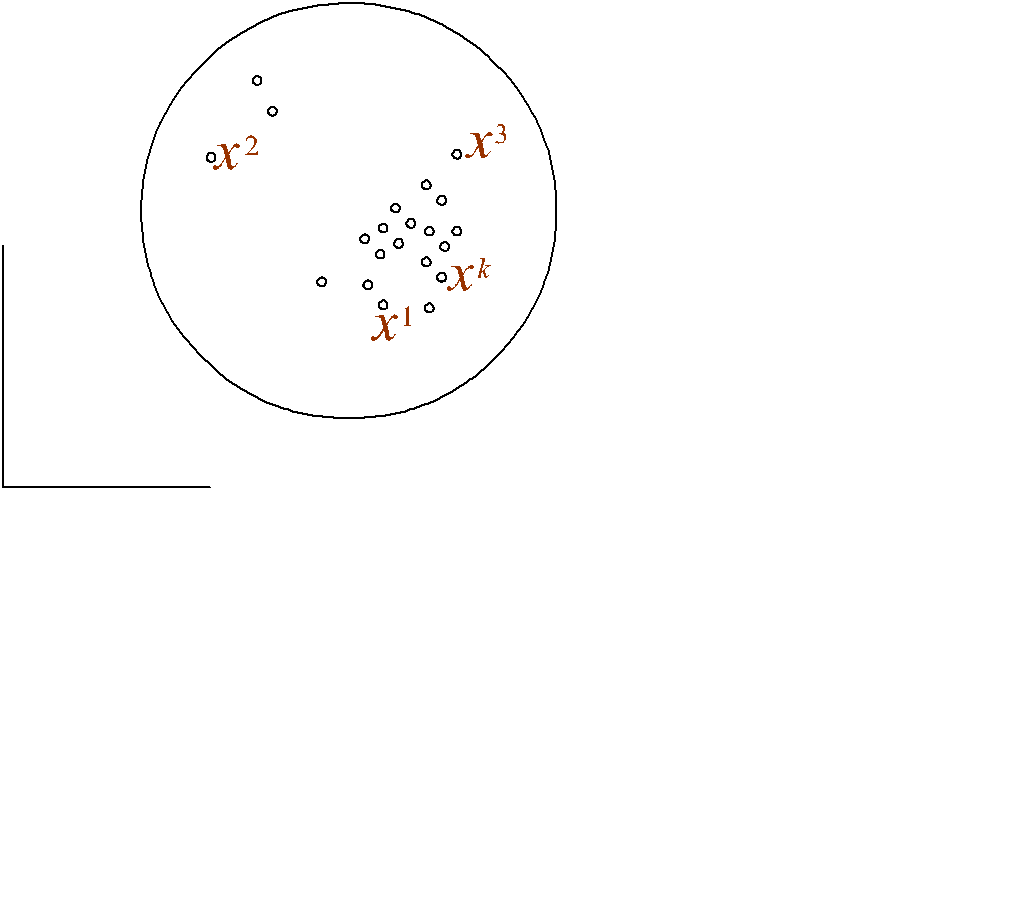
Рис. 4.5

Компакт – замкнутое, ограниченное множество.

Диагональ множества M – величина, определяемая равенством d(M)= .