Теорема (Критерий Коши). Для сходимости интеграла 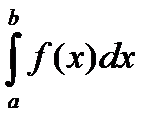 с особенностью в точке b необходимо и достаточно, чтобы
с особенностью в точке b необходимо и достаточно, чтобы
"e>0$d>0"x¢, x¢¢,b - d < x¢, x¢¢ < b: 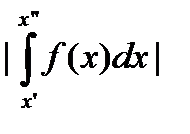 <e.
<e.
Эта теорема непосредственно следует из критерия Коши существования конечного предела 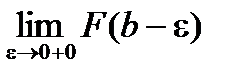 =
= 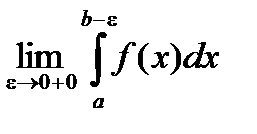
"e>0$d>0"x¢,x¢¢, b - d < x¢, x¢¢ <b:|F(x¢¢)-F(x¢)|<e.
Теорема 1 (Простой признак сравнения для несобственного интеграла от неотрицательных функций). Если 0 £ f(x) £ g(x) , то
сходится 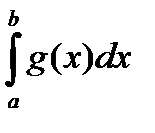 Þ сходится
Þ сходится 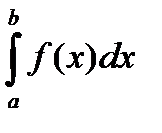
расходится 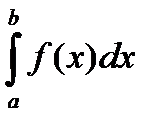 Þ расходится
Þ расходится 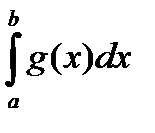
Доказательство. Утверждение непосредственно следует из соотношений (считаем x¢< x¢¢)
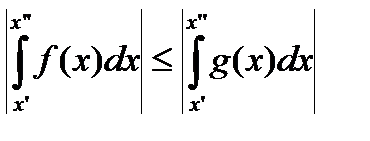 .
.
Следствие 1. Если f(x)³ 0, g(x)³ 0 и f(x ) = O(g(x)), x ® b , то
сходится 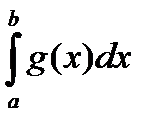 Þ сходится
Þ сходится 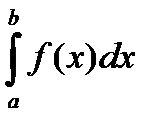
расходится 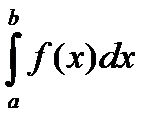 Þ расходится
Þ расходится 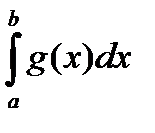 .
.
Следствие 2 (Предельный признак сравнения). Если f(x)³ 0, g(x)> 0 , 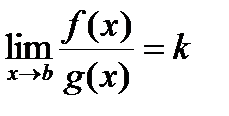 , то
, то
1) если 0< k <+ ¥ , то поведение интегралов 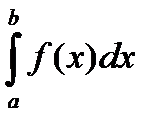 ,
, 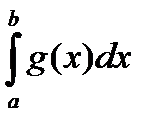 в смысле сходимости эквивалентно.
в смысле сходимости эквивалентно.
2) если k =0, то сходимость 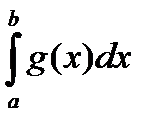 Þ сходимость
Þ сходимость 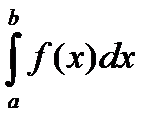 .
.
3) если k = ¥ , то расходимость 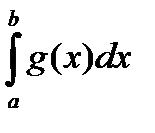 Þ расходимость
Þ расходимость 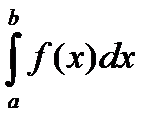 .
.
Доказательство. По определению предела для заданного e существует 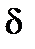 такое, что для
такое, что для
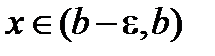 будут выполнены неравенства
будут выполнены неравенства
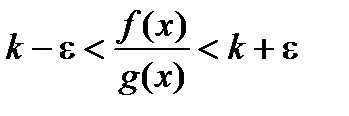 или
или
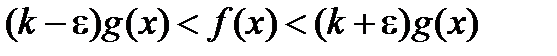 (3.2)
(3.2)
В первом случае утверждение следует из доказанной теоремы и неравенств (3.2), если взять e=k/2. В случае k =0 следует рассмотреть правое неравенство из (3.2) для какого-нибудь e, например, e=1.
Теорема 2.
Если $ c > 0 $ p < 1 " x , xÎ[a , b) : 0 £ f(x)£ 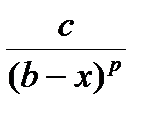 , то интеграл
, то интеграл 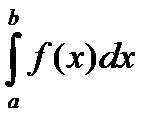 сходится.
сходится.
Если $ c > 0 $ p³ 1 " x , xÎ[a , b): f ( x)³ 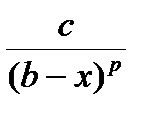 , то интеграл
, то интеграл 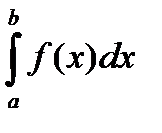 расходится.
расходится.
Утверждение следует из простого признака сравнения.
Теорема 3 ( Второй предельный признак сравнения). Если существует 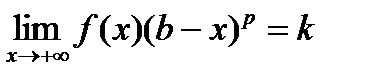 , (0 < k < +¥), то
, (0 < k < +¥), то
при p < 1 интеграл 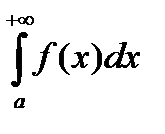 сходится,
сходится,
при p ³ 1 интеграл 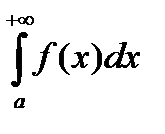 расходится.
расходится.
При k = 0 и p < 1 интеграл сходится,
при k = + ¥ , p ³ 1 интеграл расходится.
Утверждение теоремы следует из первого предельного признака сравнения.
Замечание. Аналогичные утверждения (Теоремы 1-3 и следствия имеют место для интегралов с особенностями в левом конце или во внутренней точке.
Пример 1. 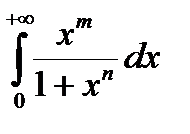 .
.
Пример 2. 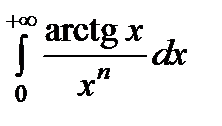
Пример 3. 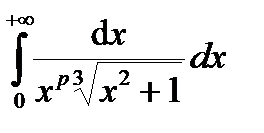
3.2. Абсолютная и условная сходимость несобственного интеграла. Признаки сравнения.
Абсолютная и условная сходимость. Интегрирование по частям, замена переменного. Формулы Эйлера.
Определение
Несобственный интеграл 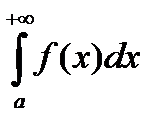 (или
(или 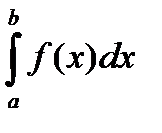 )называется абсолютно сходящимся, если сходится интеграл
)называется абсолютно сходящимся, если сходится интеграл 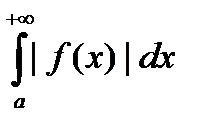 (или, для интеграла 2-го рода,
(или, для интеграла 2-го рода, 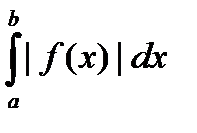 ).
).
Критерий Коши абсолютной сходимости. Для абсолютной сходимости интеграла первого рода 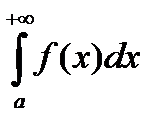 необходимо и достаточно выполнение условия
необходимо и достаточно выполнение условия
"e>0 $ M " R¢,R¢¢, M< R¢ < R¢¢ : 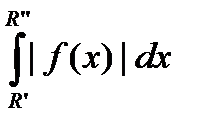 <e.
<e.
Для абсолютной сходимости интеграла второго рода 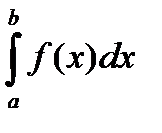 с особенностью в точке b необходимо и достаточно выполнение условия
с особенностью в точке b необходимо и достаточно выполнение условия
"e>0 $d "x¢, x¢¢, b - d < x¢ < x¢¢ < b: 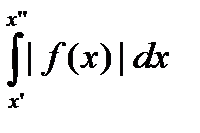 <e.
<e.
Замечание. Абсолютно сходящийся интеграл сходится.
Это следует из неравенства 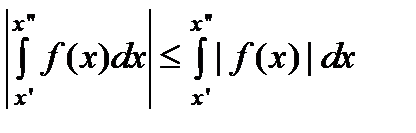 и критерия Коши.
и критерия Коши.
Обратное, вообще говоря, неверно.
Пример. 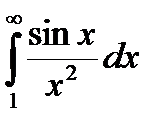 ,
, 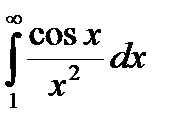 сходятся абсолютно, так как для подинтегральных функций справедливы неравенства
сходятся абсолютно, так как для подинтегральных функций справедливы неравенства 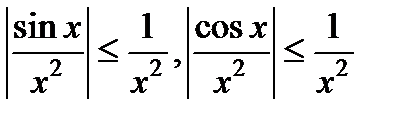 .
.
Пример. Интеграл 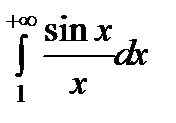 сходится. Действительно,
сходится. Действительно,
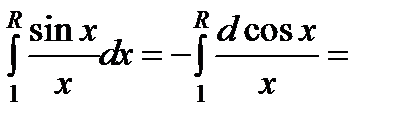
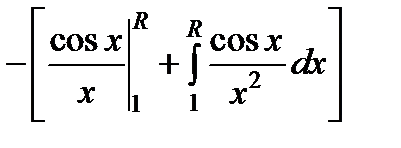 .
.
Пример. Интеграл 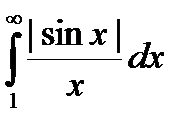 расходится.
расходится.
Действительно, для интеграла 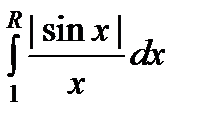 можно записать следующее неравенство
можно записать следующее неравенство
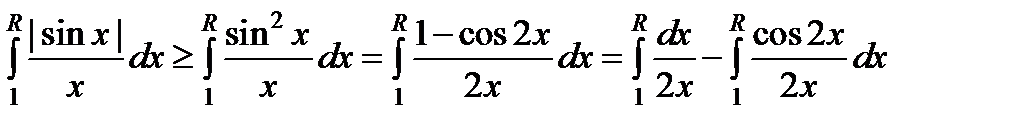 .
.
Так как интеграл 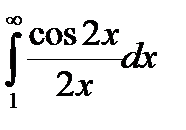 сходится, а второй интеграл
сходится, а второй интеграл 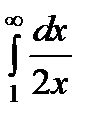 расходится, то и интеграл
расходится, то и интеграл 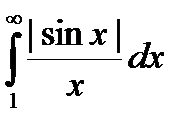 будет расходящимся.
будет расходящимся.
Определение. Несобственный интеграл 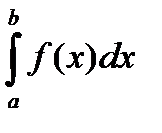 ( или
( или 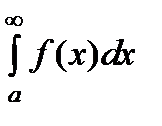 ) называются условно сходящимся, если
) называются условно сходящимся, если 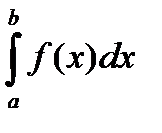 (или
(или 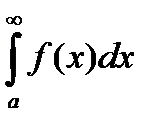 ) сходится, а интеграл
) сходится, а интеграл 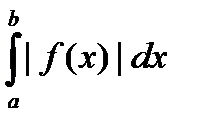 (или
(или 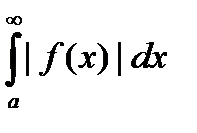 ) расходится.
) расходится.
Пример. Интеграл 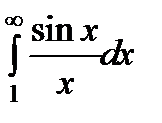 , как это следует из предыдущих примеров, сходится условно.
, как это следует из предыдущих примеров, сходится условно.
Теорема (Признак Абеля). Пусть f и g определены на [a ,+¥). f(x) интегрируема на [a ,+ ¥), g(x) монотонна и ограничена , тогда 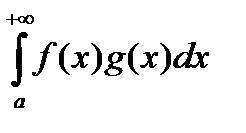 сходится .
сходится .
Доказательство. По третьей теореме о среднем (R ¢ < R ¢¢)
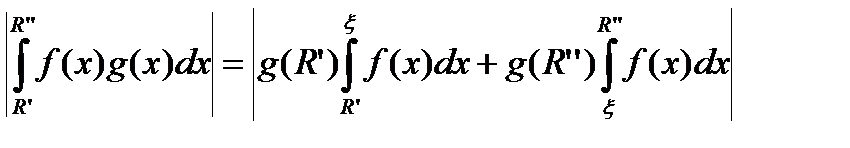 .
.
Правую часть в этом равенстве можно сделать сколь угодно малой выбором достаточно больших 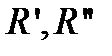 .
.
Теорема (Признак Дирихле). Пусть f и g определены на [a ,+¥).
1) f(x) непрерывна и имеет ограниченную первообразную
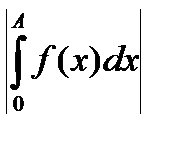 £ K , для " A³a ,
£ K , для " A³a ,
2) g(x) монотонна и стремится к 0 при x ® ¥ ,
тогда 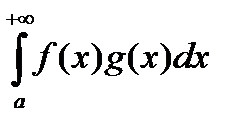 сходится.
сходится.
Доказательство. По третьей теореме о среднем (R ¢ < R ¢¢)
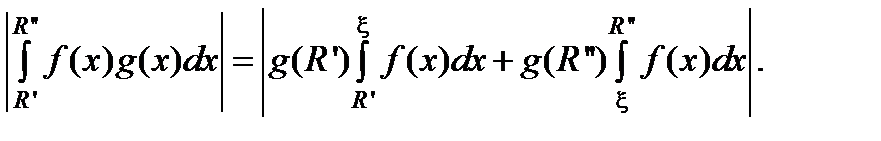
Правую часть в этом равенстве можно сделать сколь угодно малой выбором достаточно больших 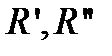 .
.
.
Пример. 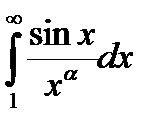 ,a>0, сходится по признаку Дирихле. Для этого в качестве функции
,a>0, сходится по признаку Дирихле. Для этого в качестве функции 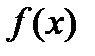
нужно взять sin x , а в качестве функции g(x) нужно выбрать функцию 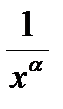 .
.
Дата: 2019-03-05, просмотров: 410.