Теорема (Критерий Коши). Для сходимости интеграла 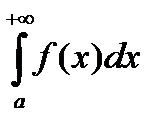 необходимо и достаточно, чтобы "e>0$M"R¢,R¢¢, R ¢ > M , R¢¢ >M :
необходимо и достаточно, чтобы "e>0$M"R¢,R¢¢, R ¢ > M , R¢¢ >M : 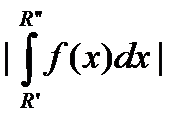 <e.
<e.
Эта теорема непосредственно следует из критерия Коши существования конечного предела 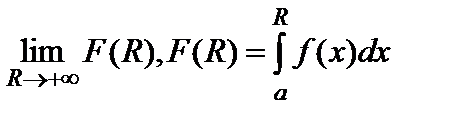 .
.
"e>0$M " R¢, R¢¢ > M:| F(R¢¢)- F(R¢)|<e.
Теорема 1 (Простой признак сравнения для несобственного интеграла от неотрицательных функций). Если 0£ f(x) £ g(x) , то
сходимость 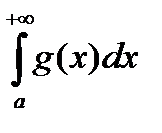 Þ сходится
Þ сходится 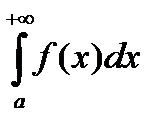
расходится 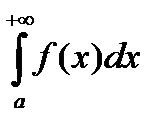 Þ расходится
Þ расходится 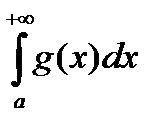
Доказательство. Первое утверждение непосредственно следует из соотношений
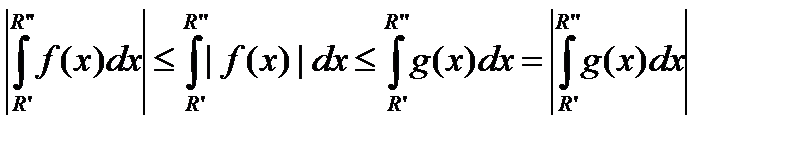
(для определенности можно считать R¢ < R¢¢ ) и критерия Коши.
Второе утверждение доказывается от противного. Если 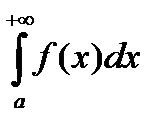 расходится, а
расходится, а 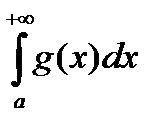 сходится, то по первому утверждению и
сходится, то по первому утверждению и 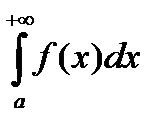 должен сходиться.
должен сходиться.
Следствие 1. Если f(x)³ 0, g(x)³ 0 и f(x)= O(g(x)), x®¥, то
сходится 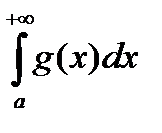 Þ сходится
Þ сходится 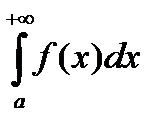
расходится 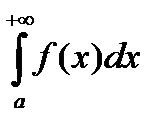 Þ расходится
Þ расходится 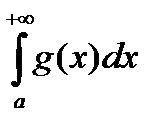 .
.
Следствие 2 (Предельный признак сравнения). Если f(x)³ 0, g ( x )> 0 , 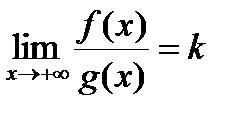 , то
, то
1) если 0<k <+ ¥ , то поведение интегралов 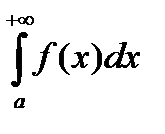 ,
, 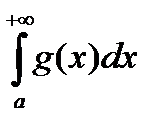 в смысле сходимости эквивалентно.
в смысле сходимости эквивалентно.
2) если k =0, то сходимость 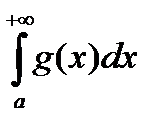 Þ сходимость
Þ сходимость 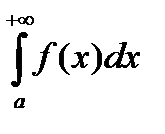 .
.
3) если k =¥, то расходимость 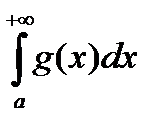 Þ расходимость
Þ расходимость 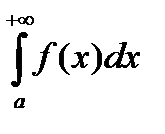 .
.
Доказательство. По определению предела для заданного e для достаточно больших x будут выполнены неравенства
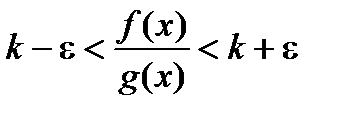 или
или
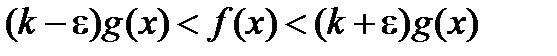 (3.1)
(3.1)
В первом случае утверждение следует из доказанной теоремы и неравенств (3.1), если взять e= k/2. В случае k =0 следует рассмотреть правое неравенство из (3.1) для какого-нибудь e, например, e=1. В случае k =¥ для B =1 найдется M такое, что при 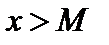 будет выполнено
будет выполнено
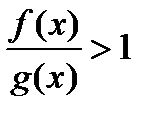 или
или 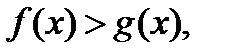 при x > M. Тогда
при x > M. Тогда 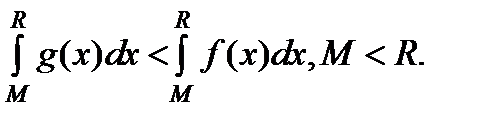 Так как
Так как 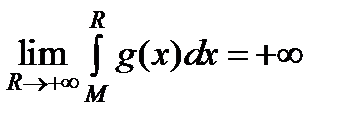 , то и
, то и 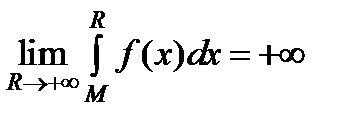 .
.
Теорема 2. Если 0 £ f(x)£ 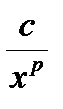 для всех x , 0 < a £ x <+¥ , где c > 0 , p > 1 , то интеграл
для всех x , 0 < a £ x <+¥ , где c > 0 , p > 1 , то интеграл 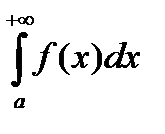 сходится.
сходится.
Если f ( x )³ 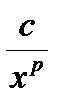 для x , 0 < a £ x <+¥ и c > 0, p£ 1 , то интеграл
для x , 0 < a £ x <+¥ и c > 0, p£ 1 , то интеграл 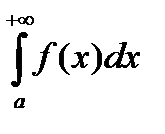 расходится.
расходится.
Утверждение следует из простого признака сравнения.
Теорема 3 ( Второй предельный признак сравнения). Если существует 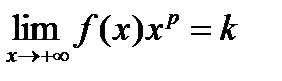 , (0 < k < +¥), то
, (0 < k < +¥), то
при p > 1 интеграл 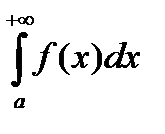 сходится,
сходится,
при p £ 1 интеграл 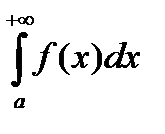 расходится.
расходится.
При k = 0 и p > 1 интеграл сходится,
при k = + ¥ , p £ 1 интеграл расходится.
Утверждение теоремы следует из первого предельного признака сравнения.
Замечание. Аналогичные утверждения (Теоремы 1-3 и следствия имеют место для интегралов вида 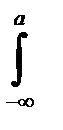 .
.
3.1.3. Несобственный интеграл второго рода
Пусть функция f(x) определена на [a , b) и интегрируема на любом [a , b -e], не ограничена в окрестности точки b .
Символ 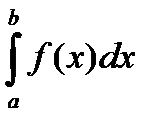 называется несобственным интегралом второго рода. Интеграл сходится, если существует конечный предел
называется несобственным интегралом второго рода. Интеграл сходится, если существует конечный предел
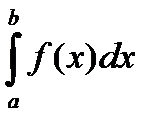 =
= 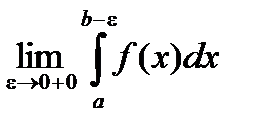 .
.
Если этот предел существует, то он называется сходящимся, иначе расходящимся.
В рассматриваемом случае, говорят об особенности в точке b (рис. 3.1, слайд «Интеграл 2-го рода, особенность справа»).
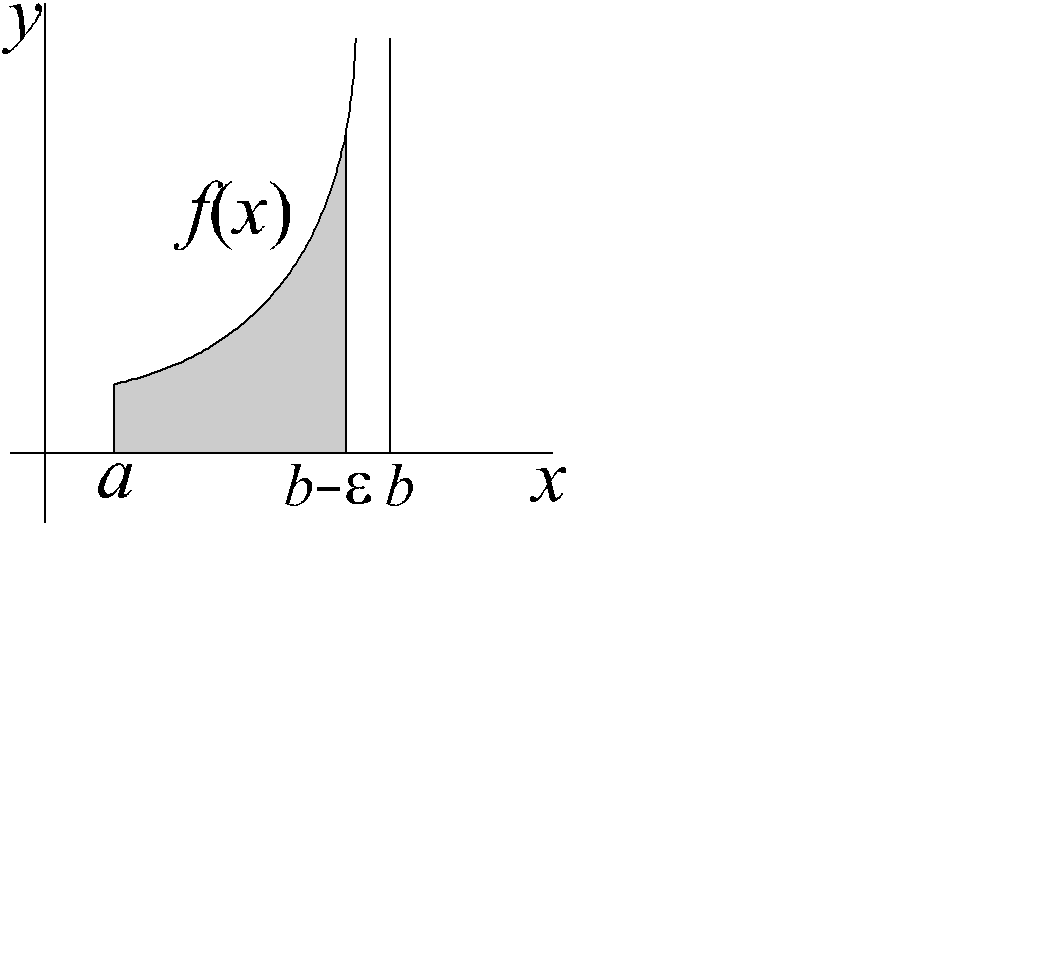
Рис. 3.1
Интеграл 2-го рода, особенность справа
Аналогично определяется интеграл 2-го рода для функции с особенностью в точке a .
Пусть функция f(x) определена на (a , b] и интегртируема на любом [a +e, b] , не ограничена в окрестности точки a .
Символ 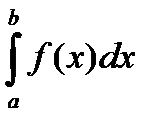 называется несобственным интегралом второго рода. Интеграл сходится, если существует конечный предел
называется несобственным интегралом второго рода. Интеграл сходится, если существует конечный предел
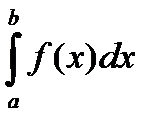 =
= 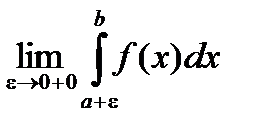 .
.
Если этот предел существует, то он называется сходящимся, иначе расходящимся (рис. 3.2, слайд «Интеграл 2-го рода, особенность слева»)
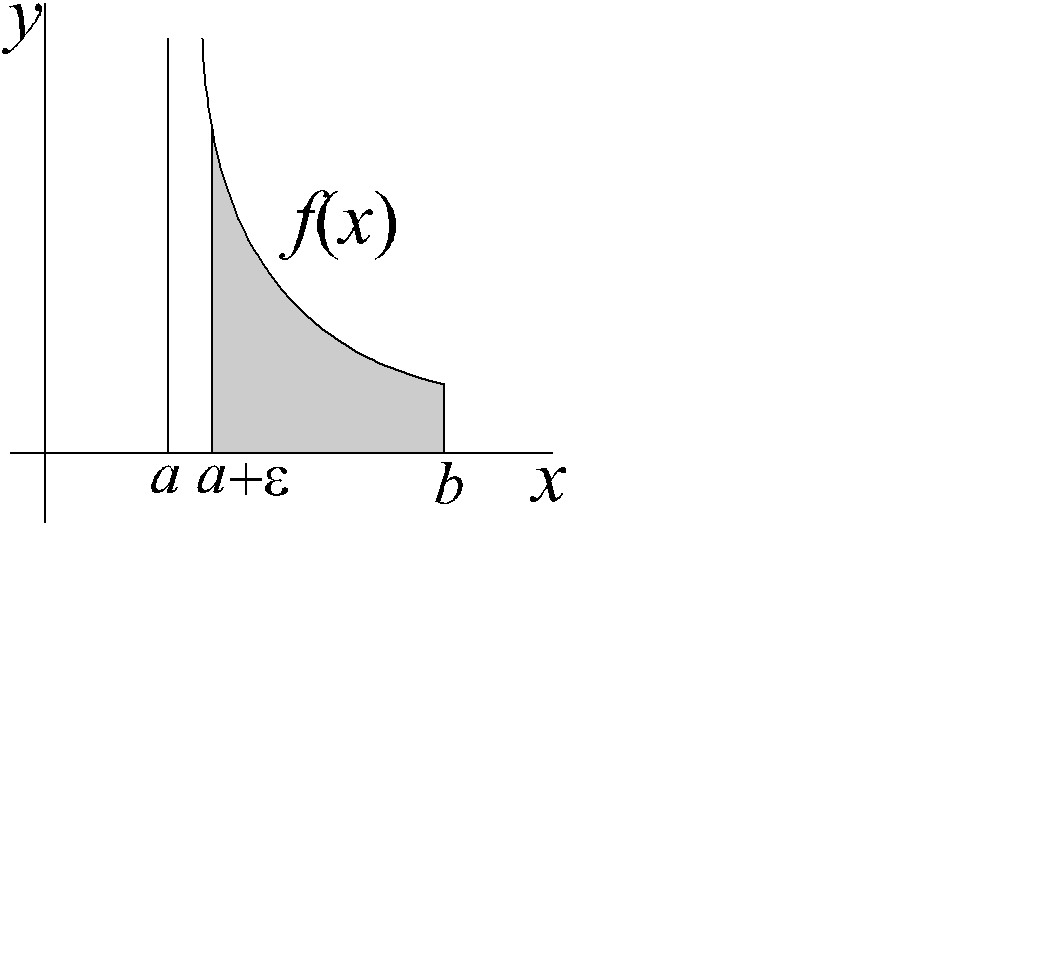
Рис. 3.2
Интеграл 2-го рода, особенность слева
Для случая с особенностью в точке b интегралы 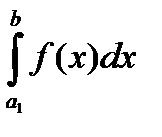 ,
, 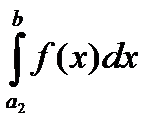 сходятся или расходятся одновременно ( a1, a2 любые числа из (a , b) ). Это следует из свойства аддитивности интеграла по множеству:
сходятся или расходятся одновременно ( a1, a2 любые числа из (a , b) ). Это следует из свойства аддитивности интеграла по множеству:
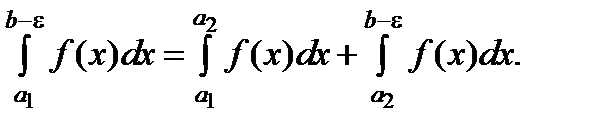
Рассмотрим теперь случай с особенность во внутренней точке cÎ (a , b ) отрезка [a , b].
Пусть f(x) определена на [a , c)È (c , b] , интегрируема на любых [a ,с-e] и [c +e, b] , не ограничена в окрестности точки c . Символ 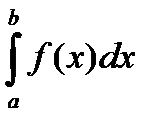 называется несобственным интегралом второго рода. Интеграл сходится, если сходятся оба интеграла
называется несобственным интегралом второго рода. Интеграл сходится, если сходятся оба интеграла 
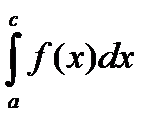 ,
, 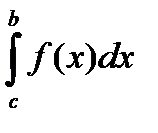 . В этом случае полагают
. В этом случае полагают
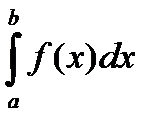 =
= 
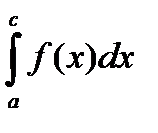 +
+ 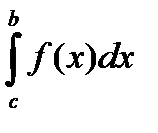 .
.
В случае расходимости одного или обоих интегралов, интеграл называется расходящимся. Из перечисленных свойств следует свойство аддитивности интеграла второго рода по множеству (рис. 3.3, слайд «Интеграл 2-го рода»).
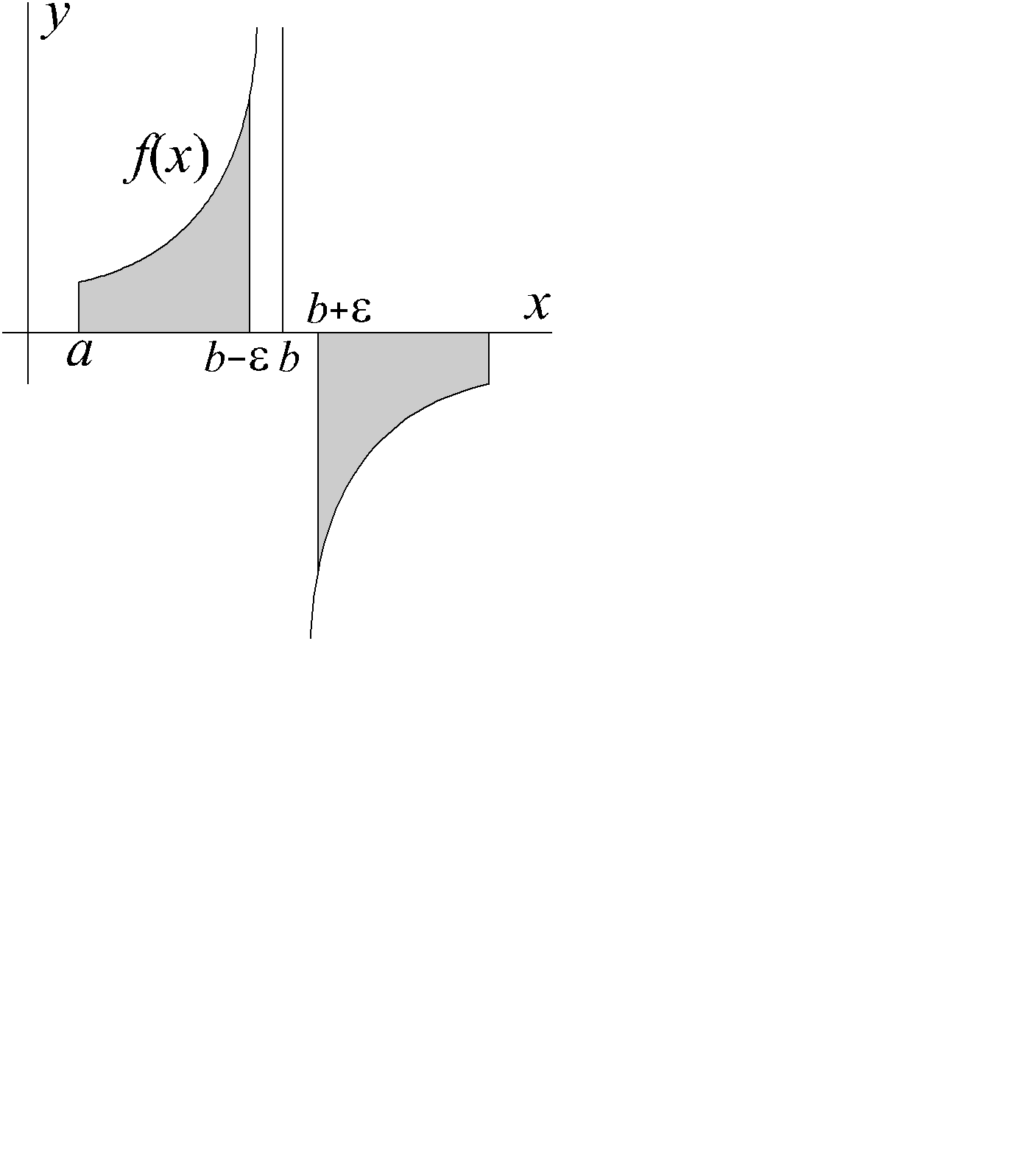
Рис. 3.3
Интеграл 2-го рода
Главным значением интеграла по Коши называется предел
V . P . 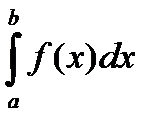 =
= 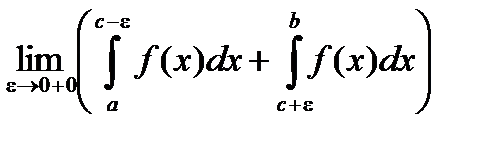 .
.
Теорема. Если существует 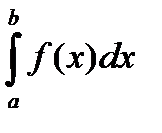 , то V . P .
, то V . P . 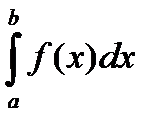 =
= 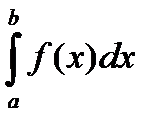 .
.
Обратное неверно. Пример. V . P . 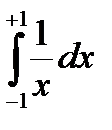 =0, в то время, как интеграл
=0, в то время, как интеграл 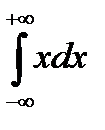 расходится.
расходится.
Пример. Интеграл 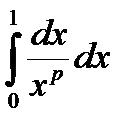 сходится при p < 1, расходится в противном случае.
сходится при p < 1, расходится в противном случае.
В более общем случае, интеграл 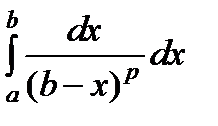 сходится при p < 1, расходится в противном случае.
сходится при p < 1, расходится в противном случае.
Пример. 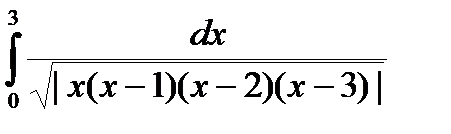 .
.
Дата: 2019-03-05, просмотров: 362.