В этом пункте мы определим площадь поверхности вращения, считая, что известно понятие площади боковой поверхности кругового конуса.
Рассмотрим развертку боковой поверхности конуса (рис. 2.33, L – образующая конуса, а R – радиус направляющей окружности (радиус основания)).
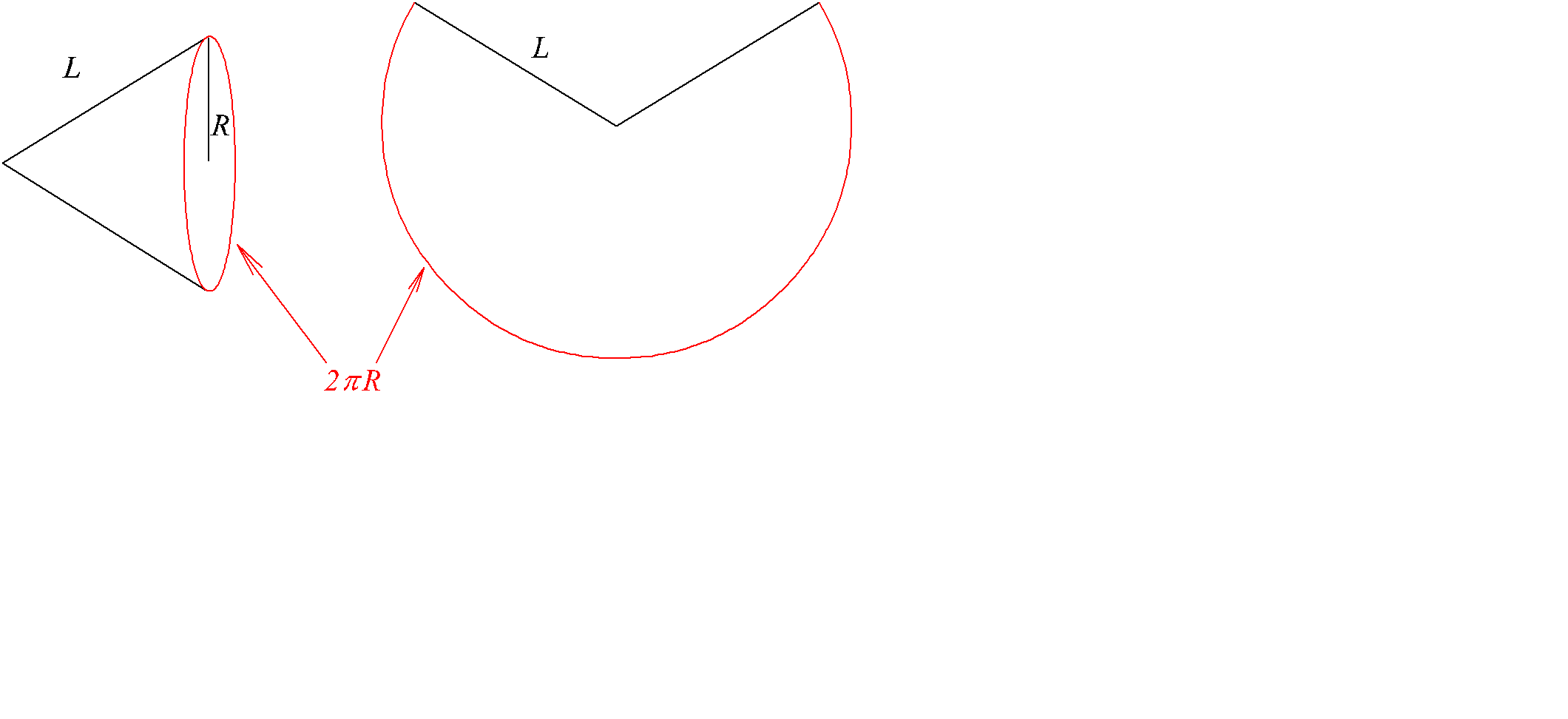
Рис. 2.33
Площадь этой развертки будет во столько раз меньше площади круга радиуса L ( 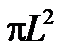 ), во сколько раз длина окружности
), во сколько раз длина окружности 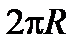 меньше длины окружности
меньше длины окружности 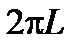 . Поэтому площадь боковой поверхности конуса равна
. Поэтому площадь боковой поверхности конуса равна 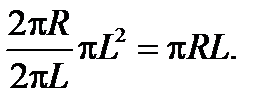
На основании этой формулы получается формула для боковой поверхности усеченного конуса (рис. 2.34)
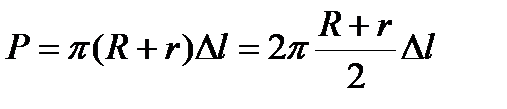 .
.
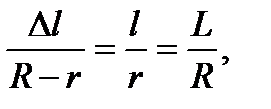
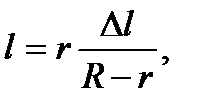
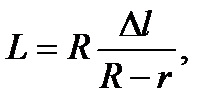
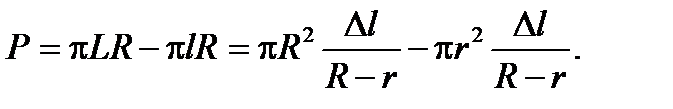
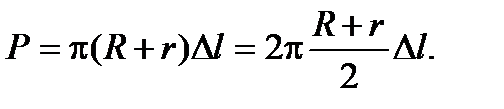
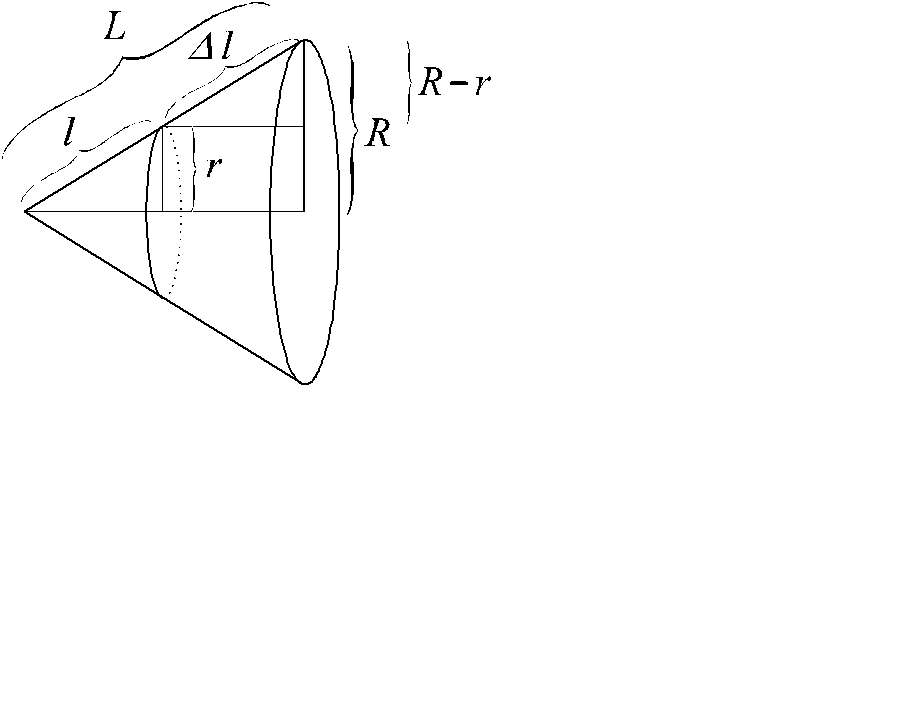
Рис. 2.34
Рассмотрим кривую g, являющуюся графиком непрерывной функции f(x)³0, определенной на [a , b]. Пусть S поверхность, полученная вращением g вокруг оси ox. Для заданного разбиения D={a = x0< x1<…< xn = b} обозначим через L(x) ломаную с узлами Ak = (xk , yk)= (xk , f(xk)), вписанную в кривую g. Через lk обозначим длину хорды Ak , Ak +1 (рис. 2.35).
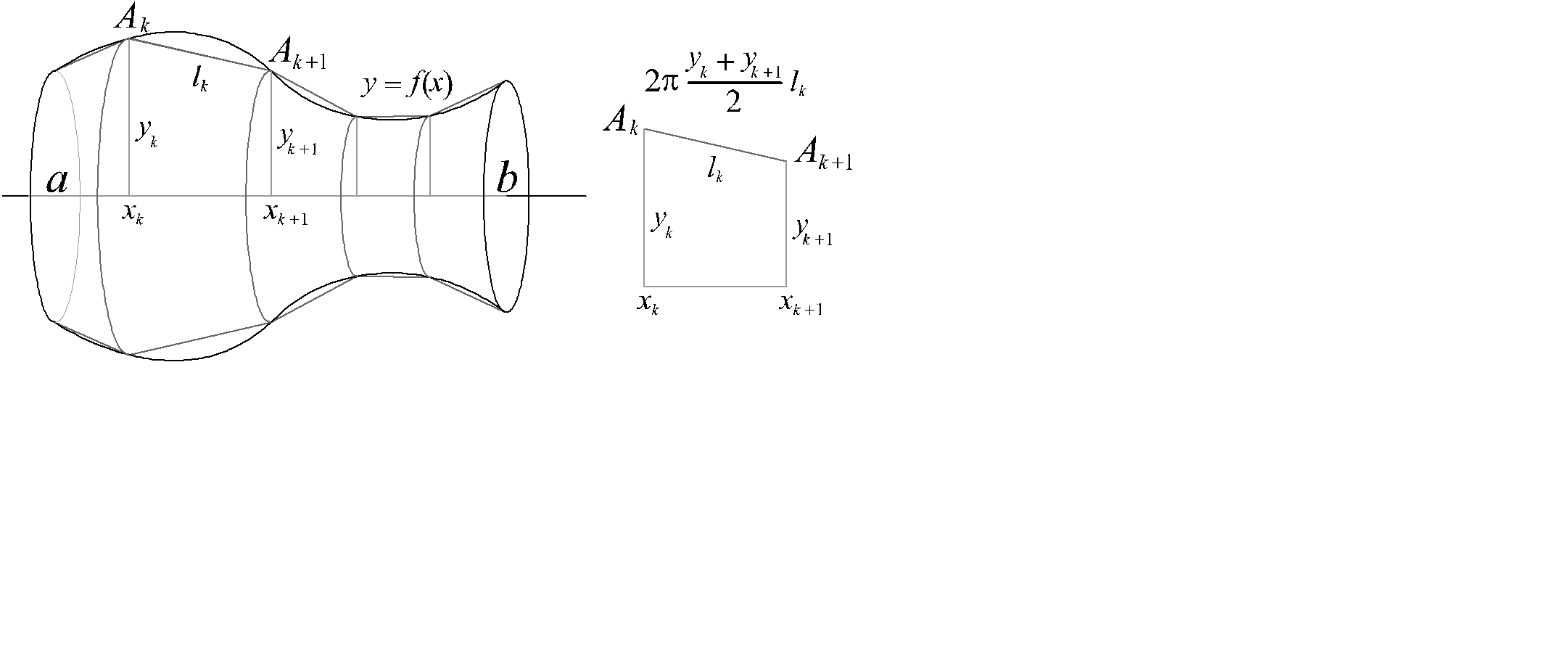
Рис. 2.35
При вращении ломаной L(x) получится поверхность, составленная из боковых поверхностей усеченных конусов, каждая из которых будет равна произведению длины окружности, описанной средней линией на длину хорды 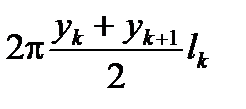 . Общая поверхность будет равна
. Общая поверхность будет равна
P(f , D)=2p 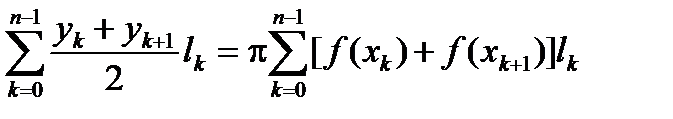 (2.11)
(2.11)
Определение. Если существует предел сумм (2.11) ( не зависящий от выбора D) при l(D)®0, то поверхность вращения называется квадрируемой и этот предел называется ее площадью.
Определение на кванторах
$S"e>0$d>0"D,l(D)<d:|P(f, D) - S |<e
Теорема. Если f(x) непрерывно-дифференцируема на [a , b], то указанная поверхность квадрируема и ее площадь равна
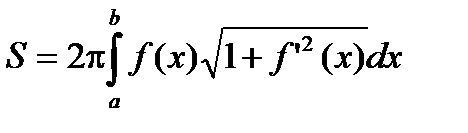 .
.
Доказательство. Для длины хорды имеем
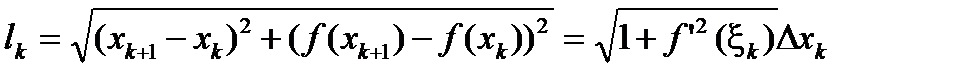 (2.12)
(2.12)
Тогда
S - P(f, D)=2p 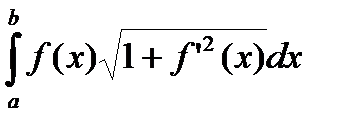 -2p
-2p 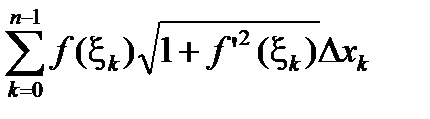 +
+
+2p 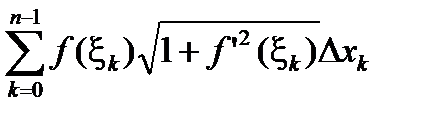 -
- 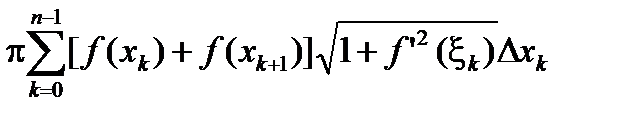 =
=
=2p 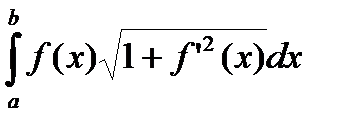 - 2p
- 2p 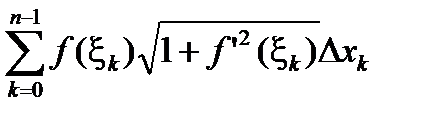 +
+
+ p 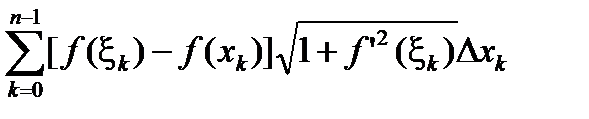 +p
+p 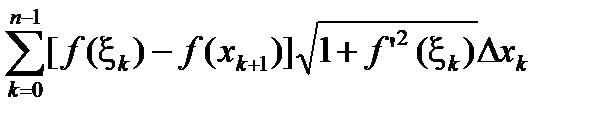 .
.
Второе слагаемое (вычитаемое) в этом выражении 2p 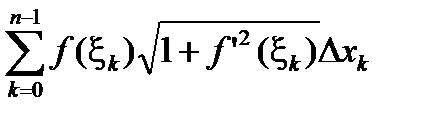 является интегральной суммой для интеграла
является интегральной суммой для интеграла 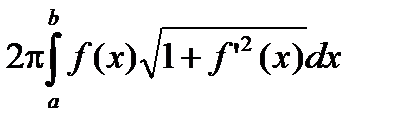 , где xk выбраны согласно (2.12). Поэтому при l(D)®0 разность 2p
, где xk выбраны согласно (2.12). Поэтому при l(D)®0 разность 2p 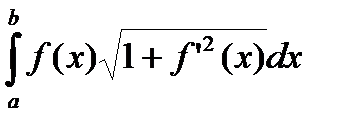 -2p
-2p 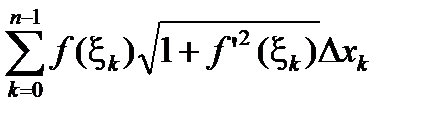 стремится к нулю в силу существования интеграла. Каждое из слагаемых
стремится к нулю в силу существования интеграла. Каждое из слагаемых
p 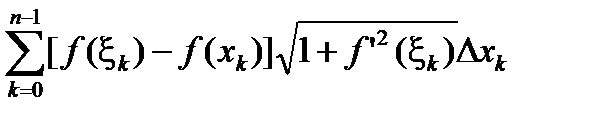 , p
, p 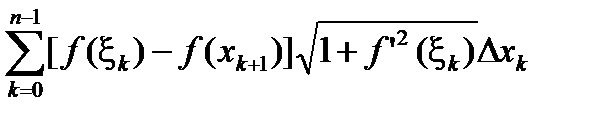
будет стремиться к нулю в силу равномерной непрерывности функции f(x) на отрезке [a , b] и ограниченности функции 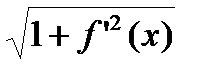 на отрезке [a , b] (первая теорема Вейерштрасса).
на отрезке [a , b] (первая теорема Вейерштрасса).
Замечание 1. Если непрерывно дифференцируемая кривая задана параметрически
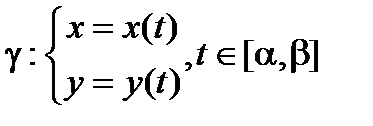 ,
,
и вращение происходит вокруг оси ox , то поверхность квадрируема и ее площадь вычисляется по формуле
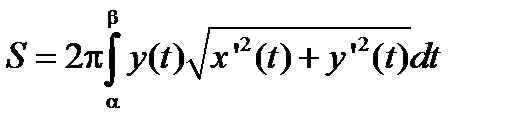 .
.
Доказательство. Вначале кривая разбивается на участки строгой монотонности функции x(t) (предполагаем, что таких участков конечное число). Пусть это будет разбиение D={a= t0< t1<…< tn =b}. Положим для краткости xk = x(tk), рис. 2.36. На каждом участке ( в силу строгой монотонности) для x(t) существует обратная функция t = t(x), xÎ[xk , xk +1] (либо xÎ[ xk +1, xk]) , k =0,…, n -1. Таким образом, имеется n однозначных ветвей: y = f(x)= y(t(x)), xÎ[xk , xk +1] (либо xÎ[ xk +1, xk]), k =0,…,n -1. Площадь поверхности, полученной вращением k-ой ветви равна (для случая xk < xk +1) 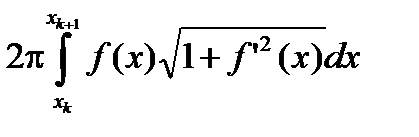 (или
(или 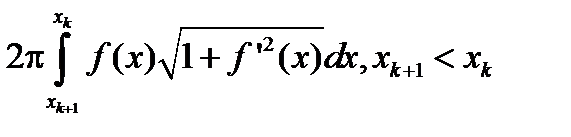 ), после замены переменного x = x(t) этот интеграл будет равен
), после замены переменного x = x(t) этот интеграл будет равен
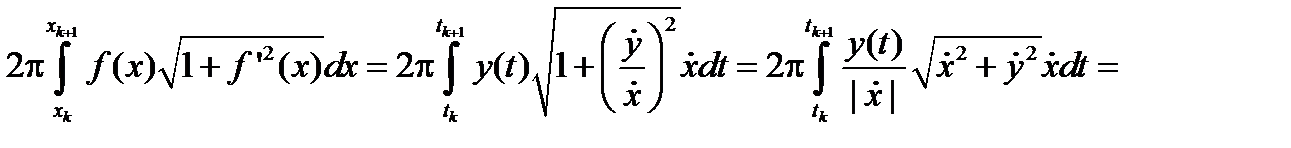
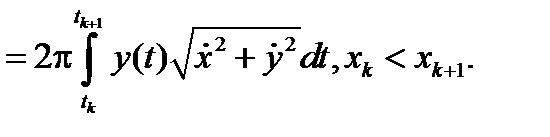
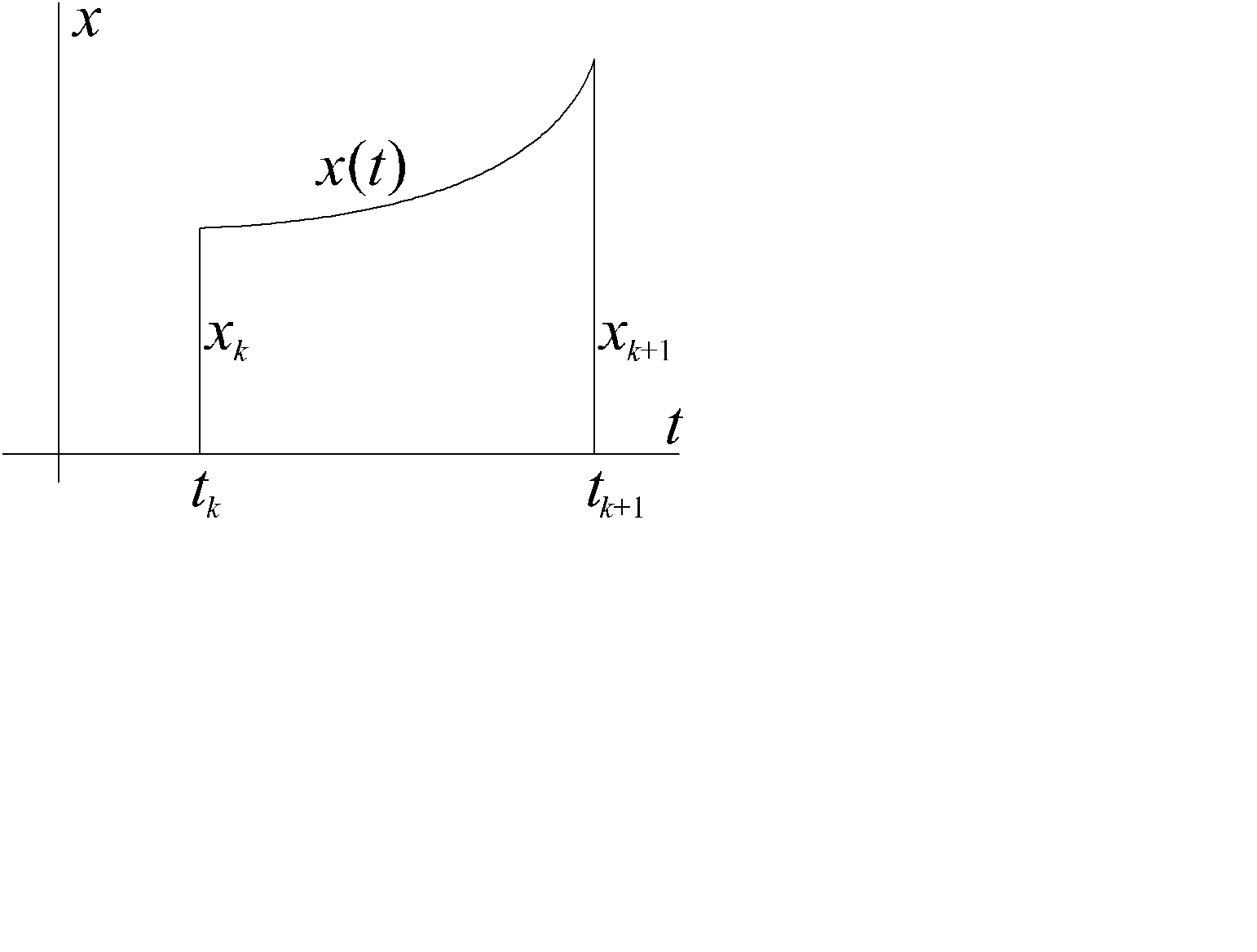
Рис. 2.36
Либо (рис. 2.37)
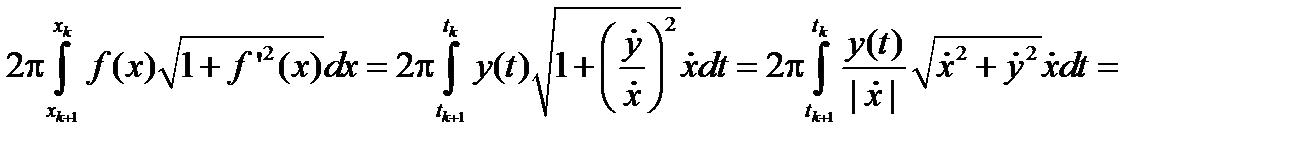
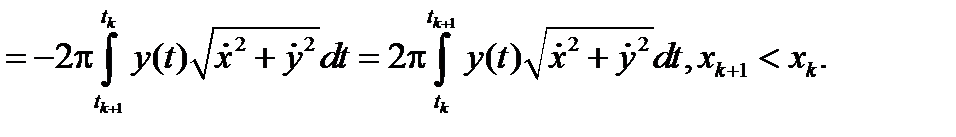
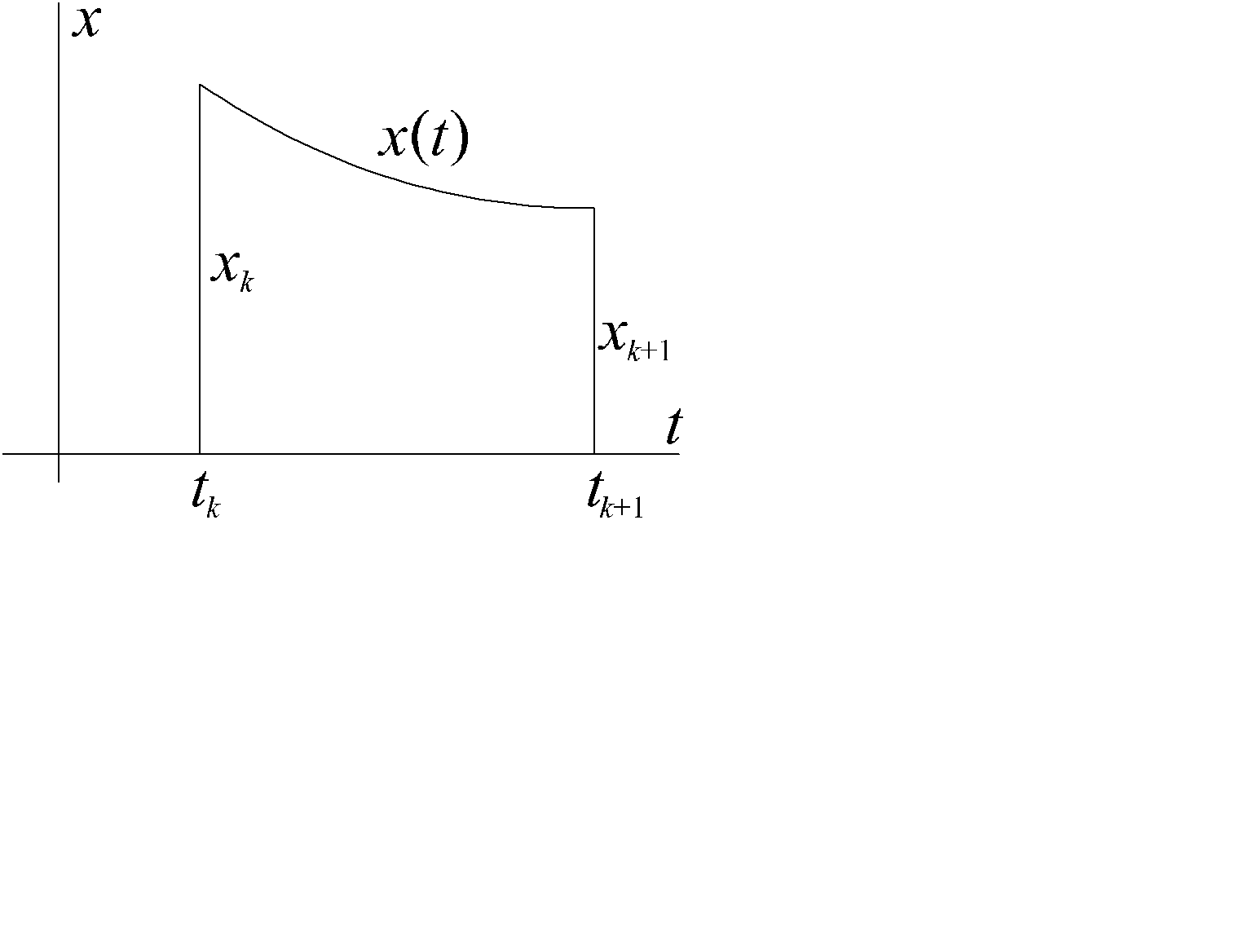
Рис. 2.37
Здесь использовано правило дифференцирования сложной фукцции и обратной функции f ¢(x)=(y(t(x))¢= 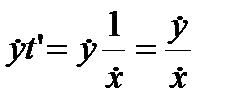 , dx =
, dx = 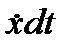 . Складывая полученные интегралы, получим требуемое соотношение
. Складывая полученные интегралы, получим требуемое соотношение
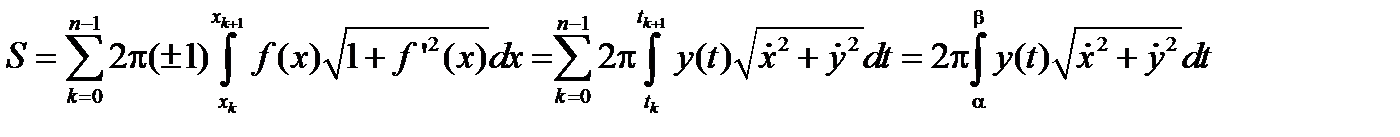 .
.
Замечание 2. Если в параметрическом задании кривой в качестве параметра взять длину дуги, то после замены переменного получим выражение для площади поверхности вращения следующего вида
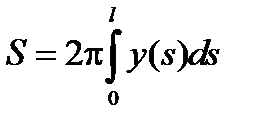 , l – длина всей кривой.
, l – длина всей кривой.
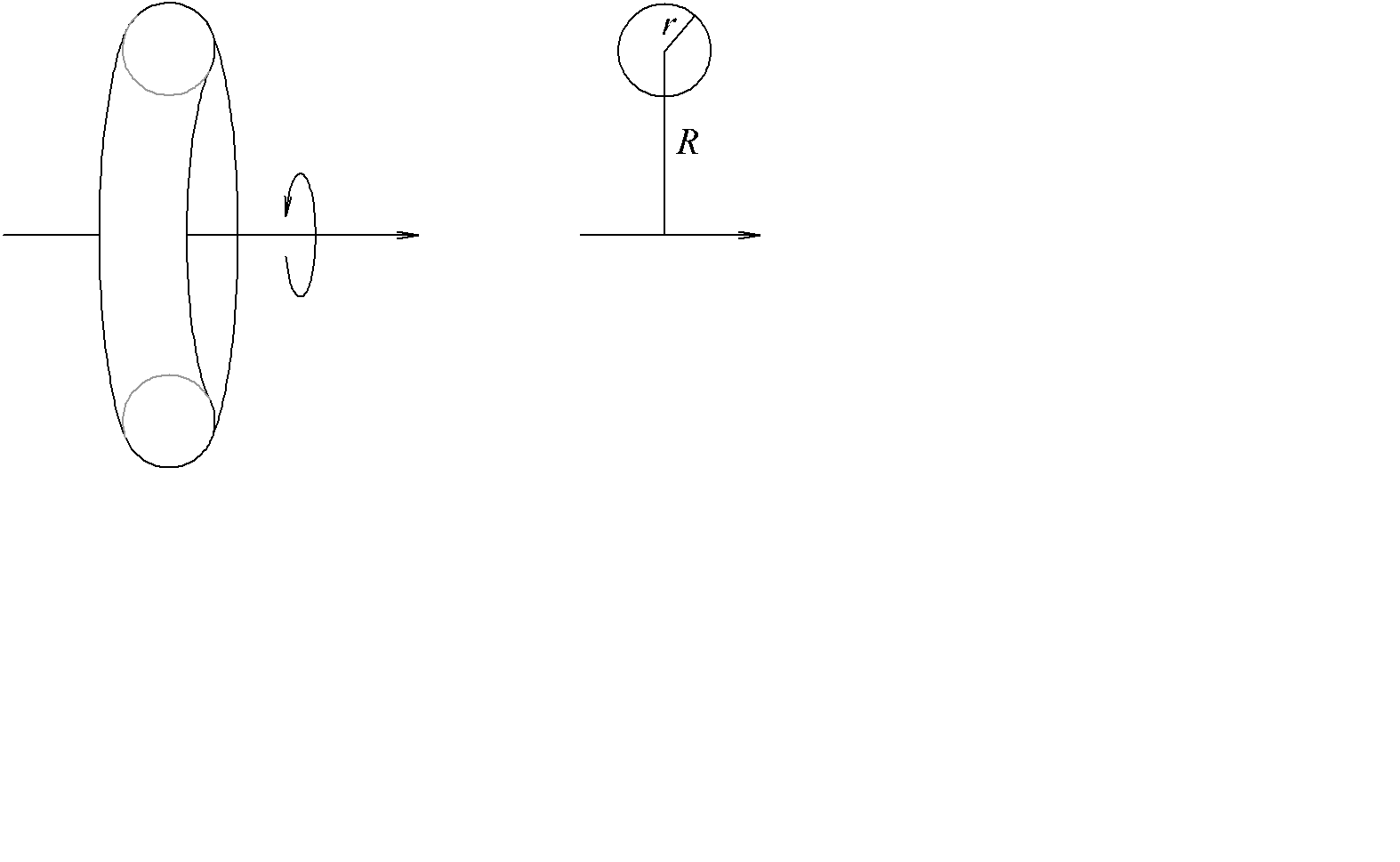
Пример. Площадь поверхности тора (рис. 2.38).
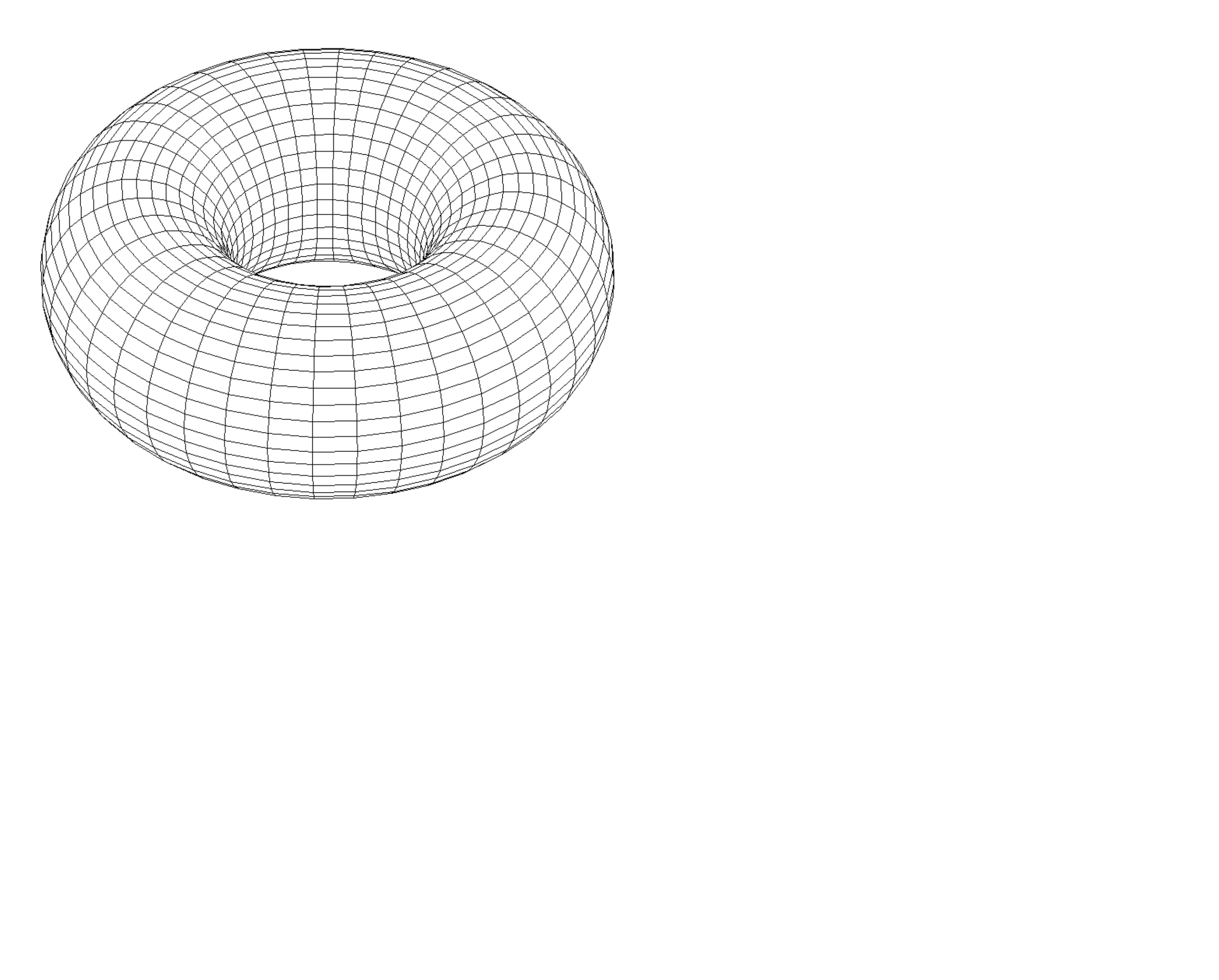
| 
|
Рис. 2.38
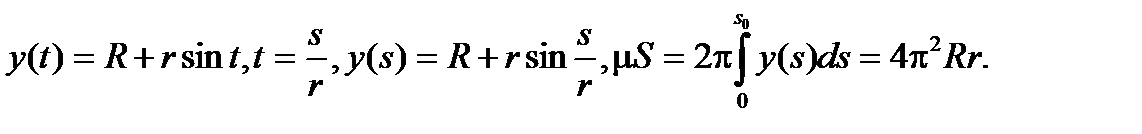
Первая теорема Гюльдена
Предположим, что масса mk расположена на расстоянии yk от оси ox (рис. 2.39). Статический момент материальной точки массы m относительно оси ox равен yk mk . Статические моменты системы из n точек относительно осей ox , oy равны
Mx = 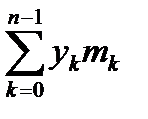 , My =
, My = 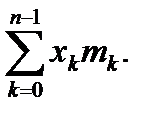
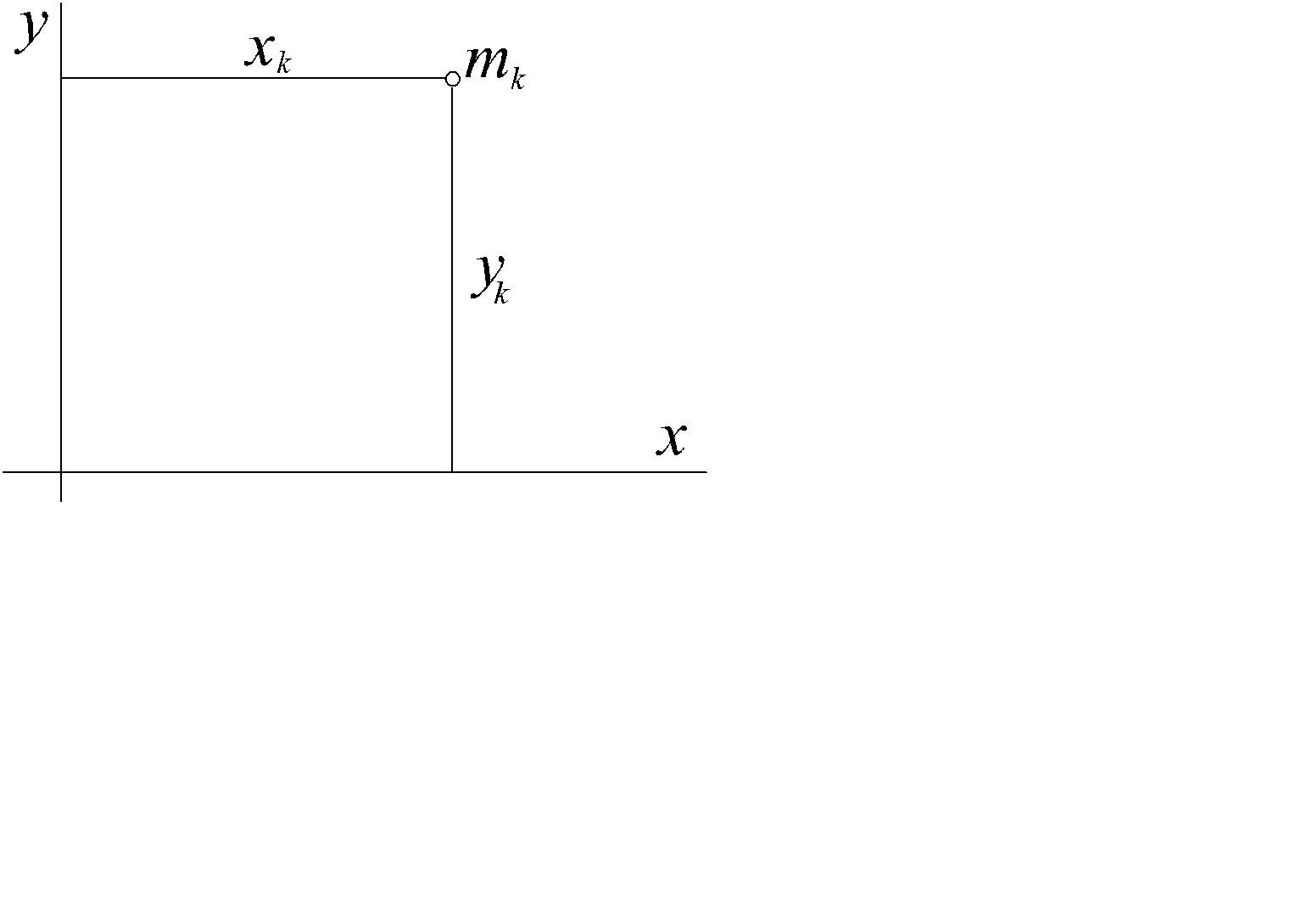
Рис. 2.39
Центр тяжести системы – это точка, обладающая следующим свойством: если в эту точку поместить сосредоточенную массу системы, то статический момент этой точки относительно любой оси совпадает со статическим моментом всей системы относительно этой оси. Выпишем равенство статических моментов дискретной системы относительно осей ox , oy .
XM = 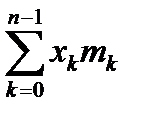 , YM =
, YM = 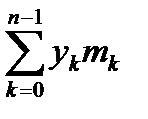 , M =
, M = 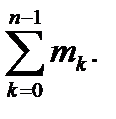
Тогда для координат центра тяжести системы получис выражения
X = 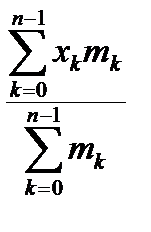 , Y =
, Y = 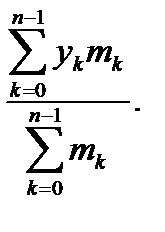 (2.13)
(2.13)
Если масса распределена вдоль кривой g :x = x(s), y = y(s), параметризованной длиной дуги и имеющей линейную плотность распределения массы r(s), то соотношения (2.13) для координат центра тяжести примут интегральный вид
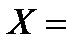
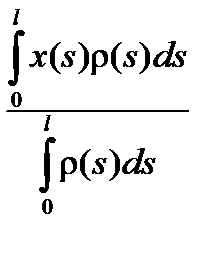 , Y =
, Y = 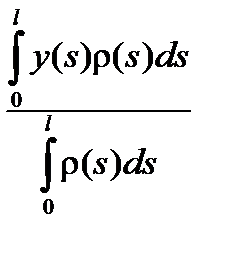 (2.14)
(2.14)
Если считать, что линейная плотность r(s)=1, то из второго равенства из (2.14) получим
2pYl =2p 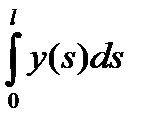 =S.
=S.
Последнее соотношение означает, что площадь поверхности, полученной вращением кривой вокруг оси c равномерно распределенной массой, равна длине этой кривой, умноженной на длину окружности, описанной центром тяжести этой кривой (первая теорема Гюльдена).
Пример. Пересчитать площадь поверхности тора по теореме Гюльдена.
Вторая теорема Гюльдена
Объем тела, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости этой фигуры и не пересекающей эту фигуру, равен произведению площади этой фигуры на длину окружности, описываемой центром тяжести этой фигуры.
Часть 3. Несобственные интегралы
3.1. Несобственный интеграл первого рода
Несобственные интегралы первого и второго рода. Критерий Коши сходимости несобственных интегралов. Признаки сходимости.
Дата: 2019-03-05, просмотров: 421.