Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Используя вписанные и описанные многоугольники можно доказать квадрируемость кругового сектора радиуса r , заключенного между двумя лучами (с углами a, b) и вычислить его площадь, равную 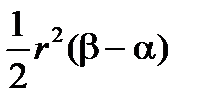 (рис. 2.18).

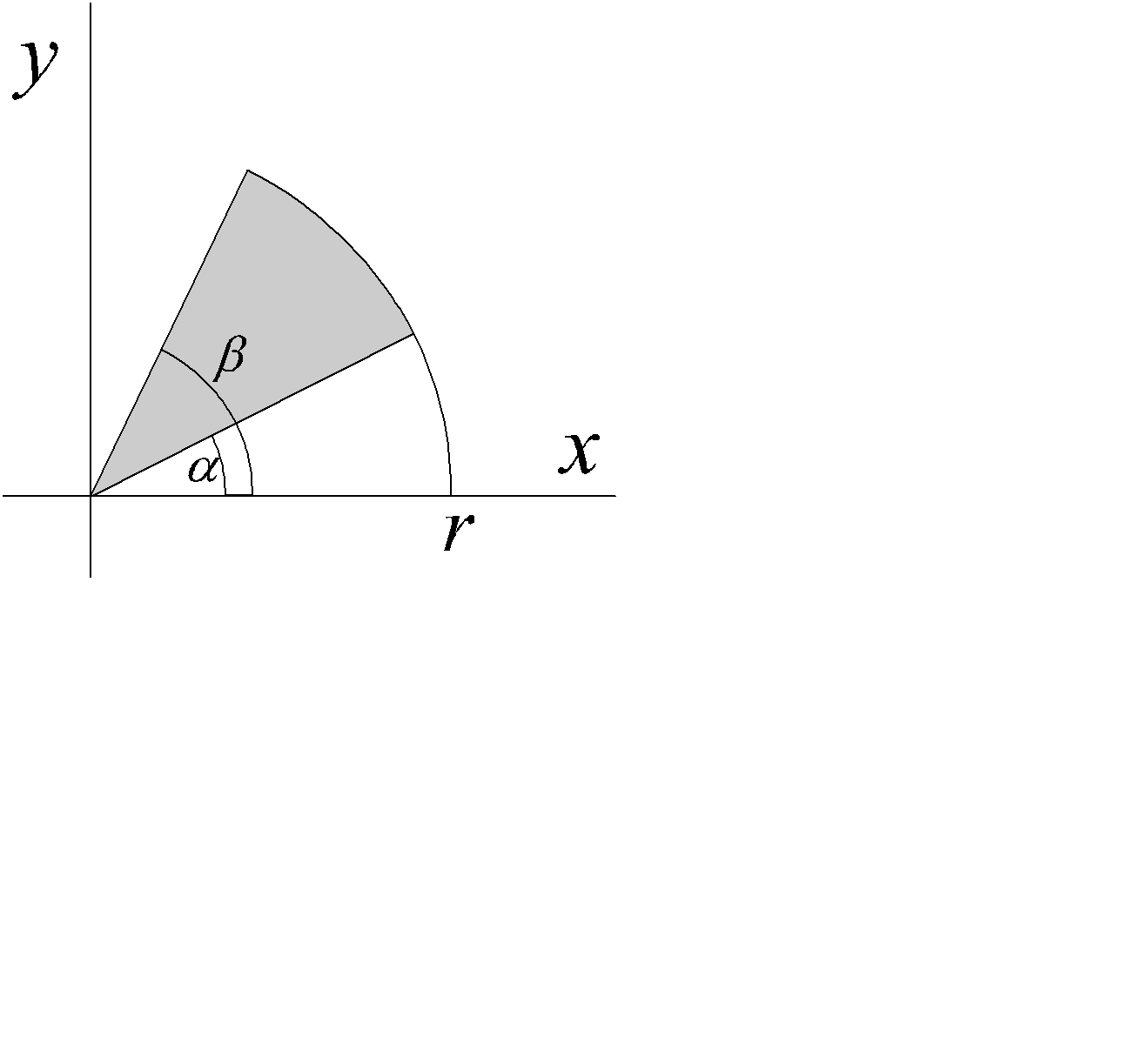
Рис. 2.18

Рассмотрим область, заключенную между лучами a, b и непрерывной кривой, заданной в полярных координатах r = r(j) ( рис. 2.19).

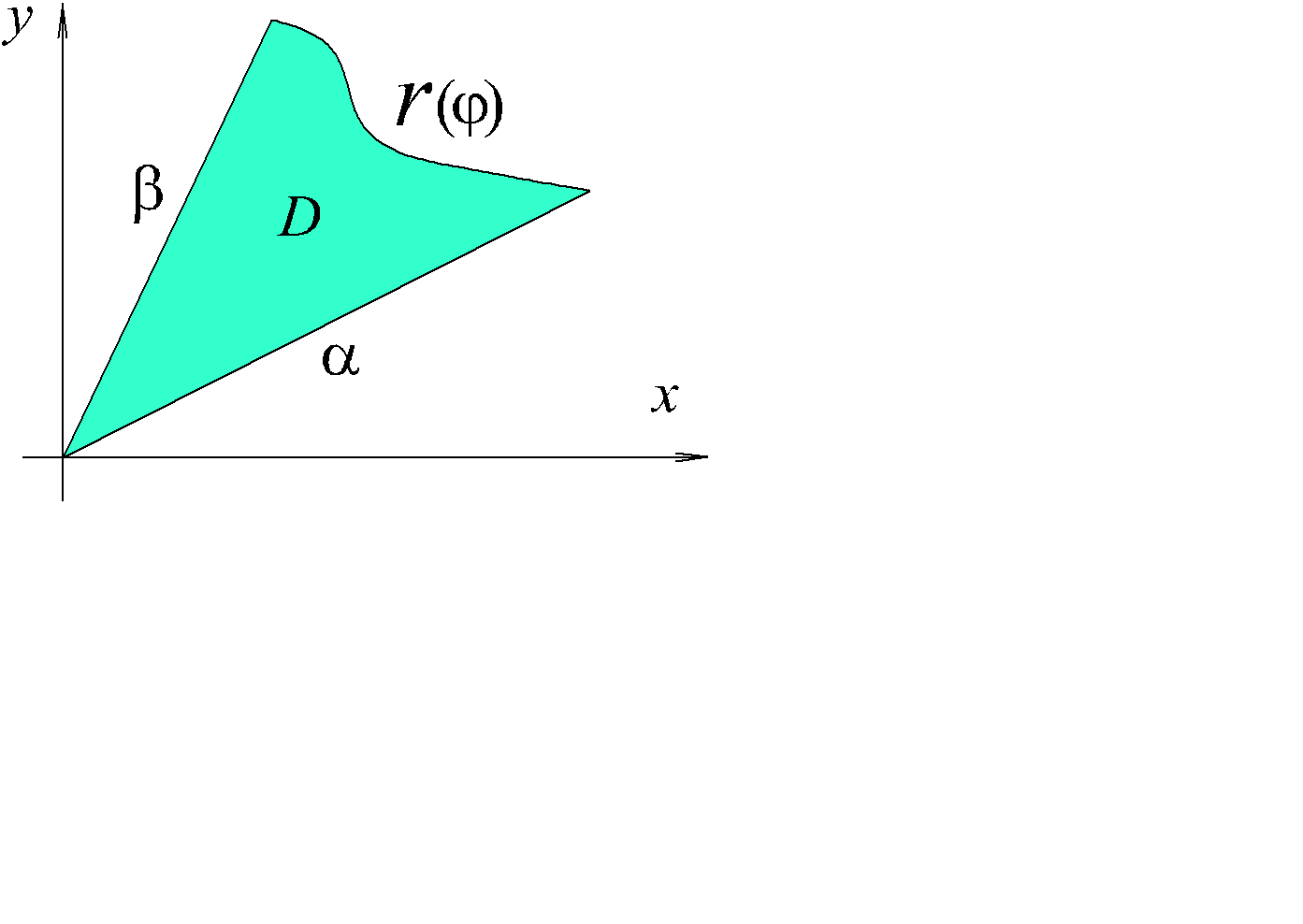
Рис. 2.19

Теорема. Криволинейный сектор D , определяемый лучами углов a, b (0≤a<b≤2π) и непрерывной кривой r = r(j) квадрируем и его площадь вычисляется по формуле (слайд «Площадь области»)

mD = .                                             (2.8)

Площадь области

Доказательство. Интеграл в (2.8) существует, поэтому для заданного e  существует разбиение D={a=j₀<j₁<…<j_n=b} отрезка 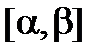 такое, что S(f ,D) – s(f,D) < e, где f(j)= 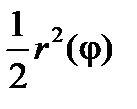. Нижняя сумма Дарбу представляет собой сумму величин вида 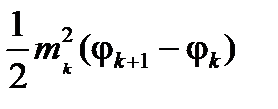, где m_k – радиус некоторого кругового сектора, вписанного в соответствующий криволинейный сектор D_k,  а верхняя сумма Дарбу представляет собой сумму величин вида 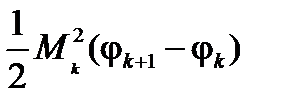, где M_k – радиус некоторого кругового сектора, содержащего D_k  (слайд «Суммы Дарбу», «Суммы Дарбу, полярные координаты»).

Суммы Дарбу

Суммы Дарбу, полярные координаты

Таким образом, для любого e  можно указать две квадрируемые области, одна из которых содержится внутри исходной области, а вторая охватывает эту область. Каждая из этих областей составлена из круговых секторов и имеет площадь равную s(f ,D), S(f ,D), соответственно. Квадрируемость следует из второго критерия квадрируемости. Выберем последовательность разбиений с равноотстоящими узлами 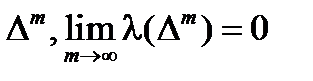. Соответствующие вписанные и описанные области, состоящие из наборов круговых секторов, обозначим  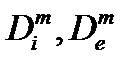. Тогда между суммами Дарбу и площадями этих множеств существует следующая связь 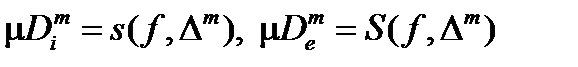. Далее  и . Эти равенства позволяют утверждать (следствие из критерия интегрируемости), что

.

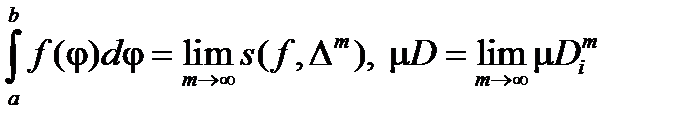Таким образом,

.

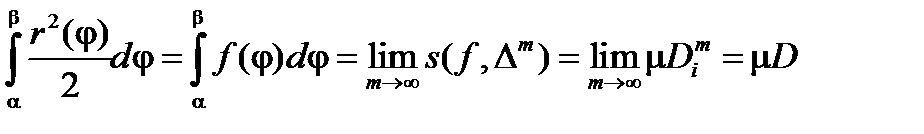     Примеры.

     5.1. Вычислить площадь области, содержащейся между первым и вторым витком спирали Архимеда 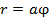, как показано на рисунке 2.20, слайд «Спираль»

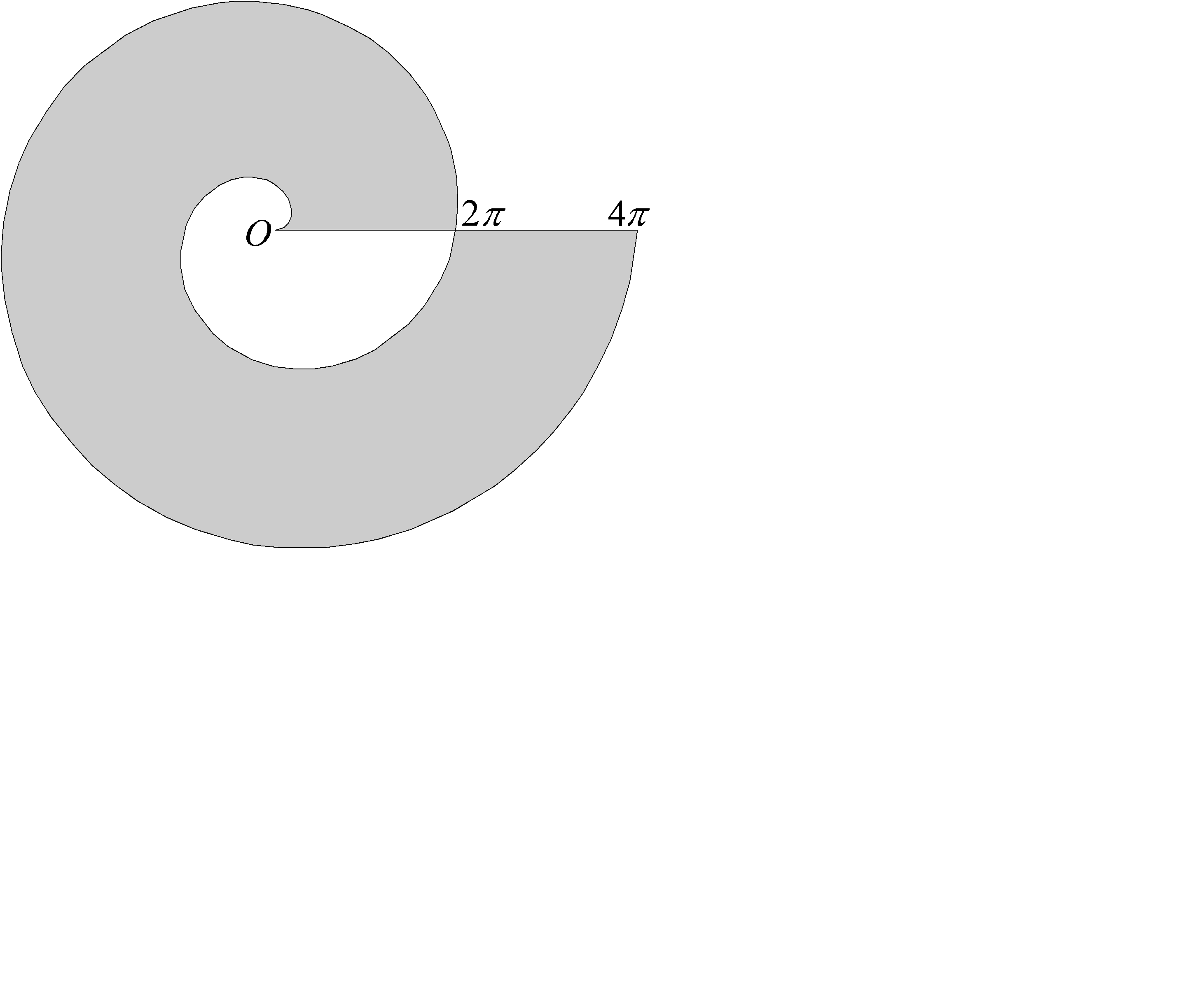
Рис. 2.20

Спираль

Площадь обозначенной на рисунке области будет равна

mD =

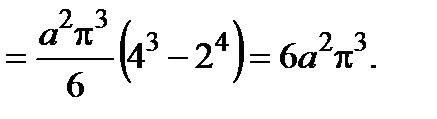
5.2. Вычислить площадь, ограниченную астроидой x^2/3+y^2/3=a^2/3.(рис. 2.21, слайд «Астроида»)

Рис. 2.21

Астроида

Воспользуемся полярными координатами 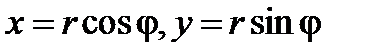. Подставляя эти выражения в исходное уравнение астроиды, получим уравнение астроиды в полярных координатах 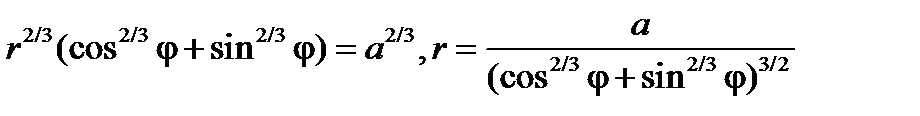. Площадь, ограниченная кривой будет равна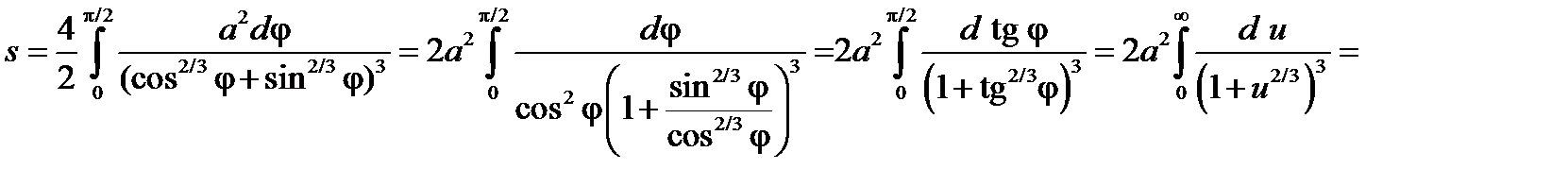

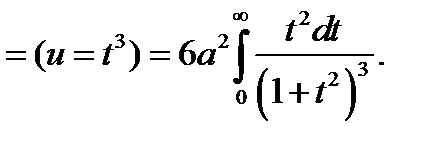 В параграфе 3 главы 1 был вычислен интеграл

.

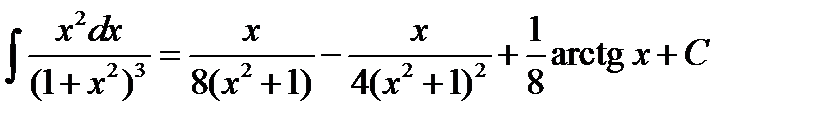Поэтому 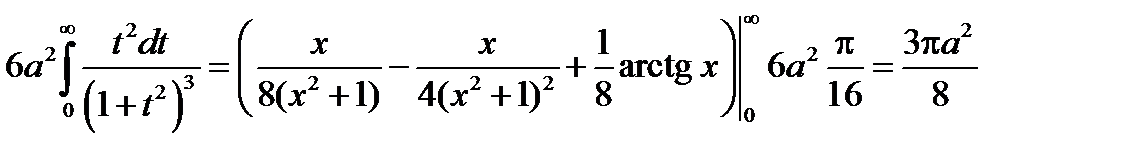. Интеграл с бесконечными пределами будет рассматриваться в разделе «Несобственные интегралы».

 

5.3.Вычислить площадь, ограниченную кривой 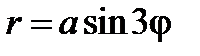 (трилистник, рис. 2.22, слайд «Трилистник»). 

                                                                         

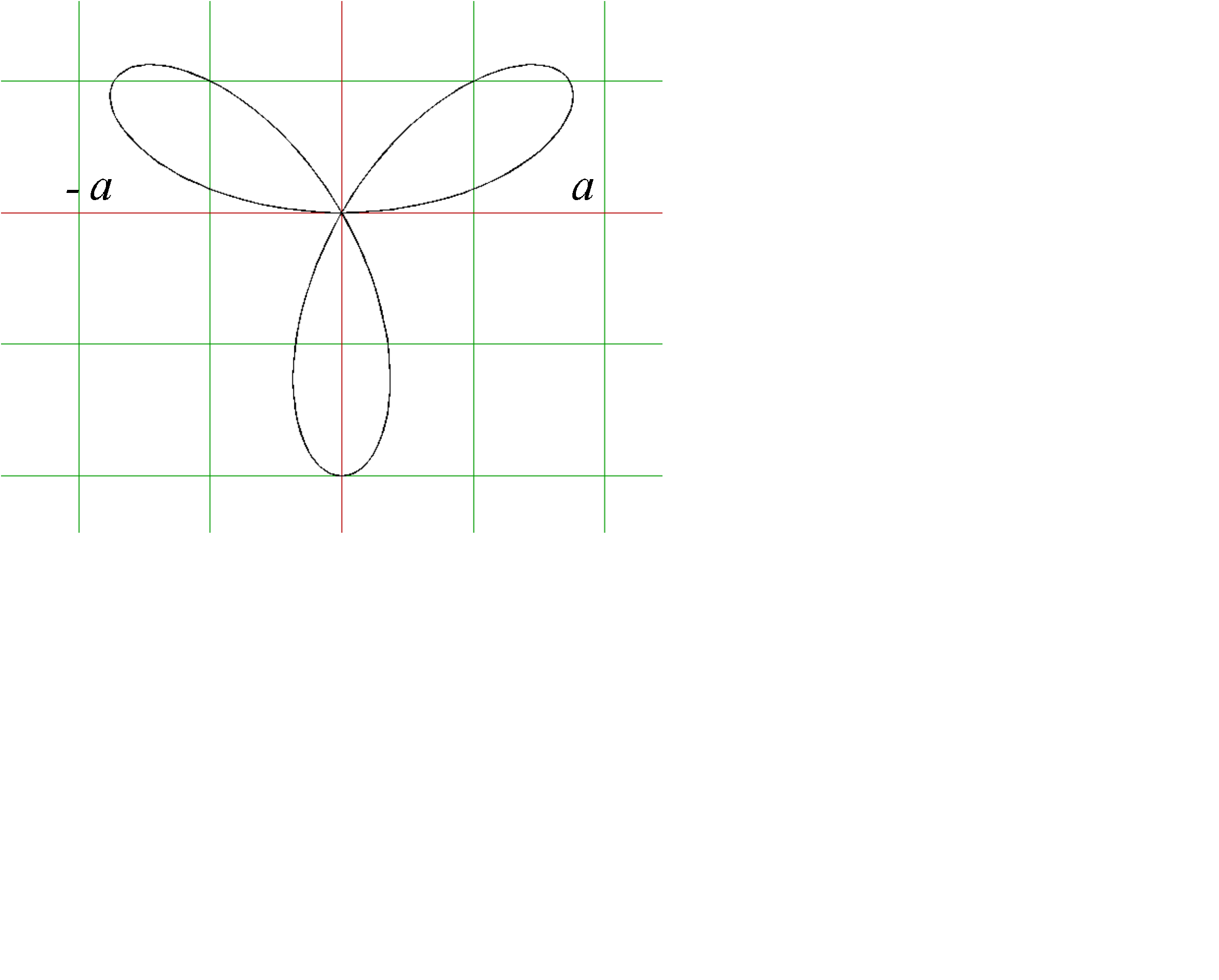
Рис. 2.22

Трилистник

Первый лепесток расположен в диапазоне 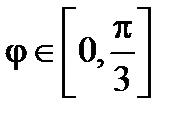, поэтому площадь трех лепестков будет равна

.

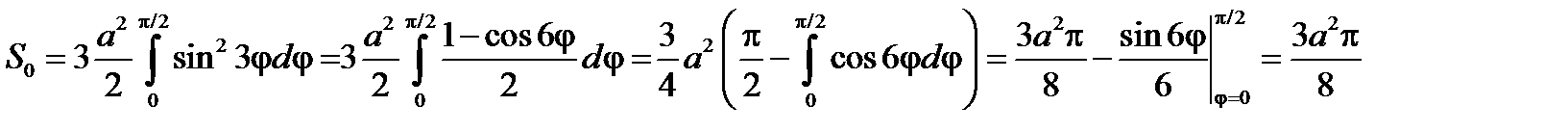5.4. Вычислить площадь, ограниченную кривой .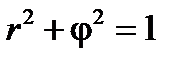

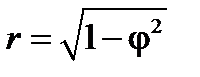, поэтому область, где расположена кривая, ограничена диапазоном 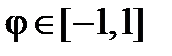. Таким образом, площадь, ограниченная кривой будет равна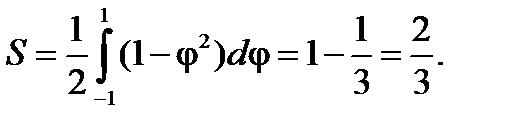

5.5.Вычислить площадь, ограниченную кривой 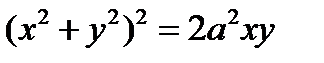(лемниската Бернули, рис. 2.23, слайд «Лемниската Бернули»).

Воспользуемся полярными координатами 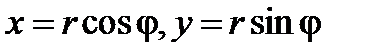. Подставляя эти выражения в уравнение лемнискаты, получим , или .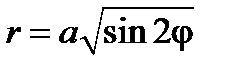

                                          

Рис. 2.23

Лемниската Бернули

.

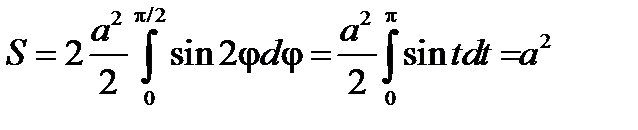2.4.5. Вычисление площади области, граница которой задана в виде φ=φ( r )

Позже будет выведена еще одна формула для вычисления площади области, граница которой задана параметрически. Именно, если область D ограничена замкнутой кусочно-гладкой кривой γ , имеющей параметризацию 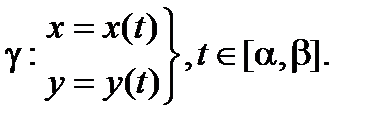 Кроме того, при проходе t от α до β область остается слева (слайд «Обход границы области»),

Обход границы области

то площадь этой области будет вычислятся по формуле:

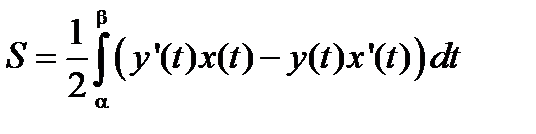                                                  .                                          (2.9)

Пусть функция φ(r) непрерывна и монотонна на отрезке [r₁, r₂] , 0≤r₁<r₂. Рассмотрим область, лежащую между лучами φ₁₌φ(r₁), φ₂₌φ(r₂) и кривой γ: φ=φ(r) (см. рис. 2.24).

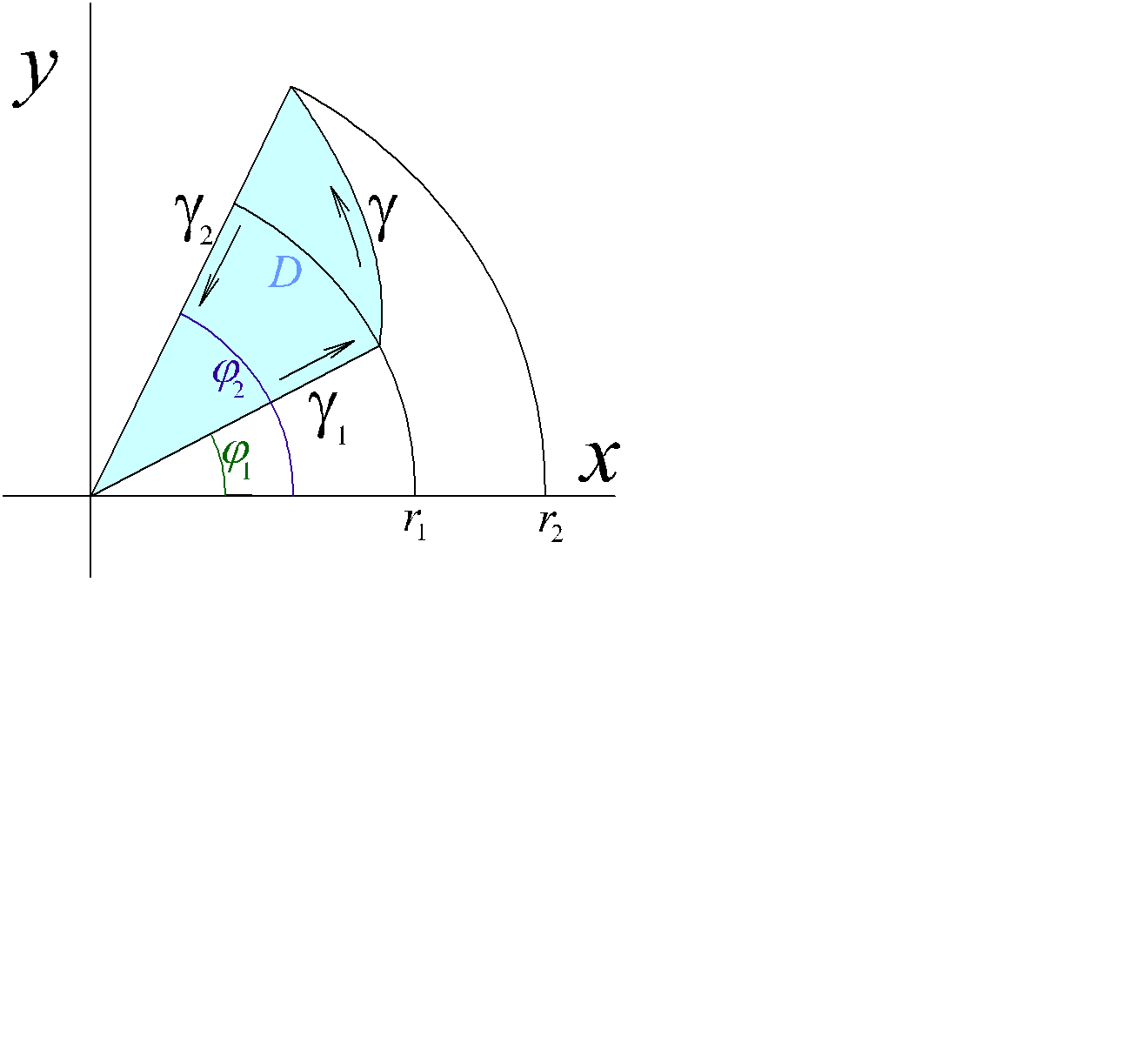
Рис. 2.24

Граница этой области состоит из трех кривых γ₁, γ, γ₂. Кривая γ₁ может быть параметризована в виде

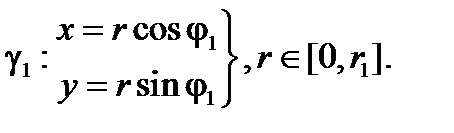
Аналогично, для кривой γ₂ (обратите внимание на направление обхода)

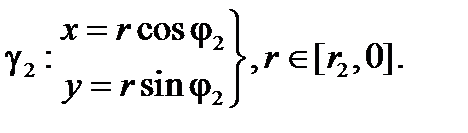
И, наконец, для кривой γ имеем:

                                                   

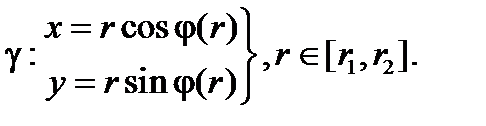
Для γ₁ подинтегральное выражение в (2.9) будет равно

                                        .

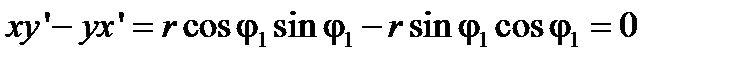И тогда

                                                          

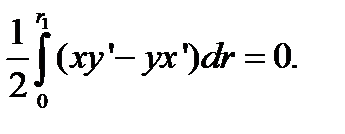
Аналогично, для γ₂ 

                                       .

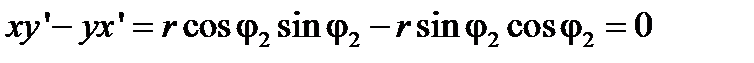И тогда

                                                          

 

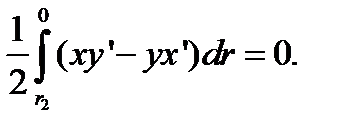
Наконец, для участка γ получим

.

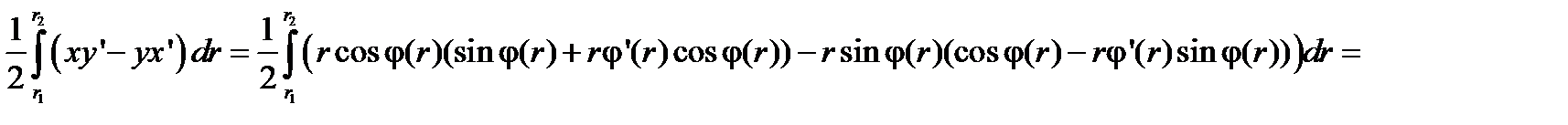
Таким образом, окончательно, получим формулу

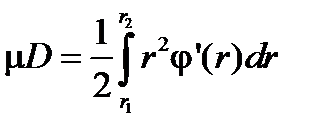                                                            .                                                  (2.10)

Пример. Найти площадь области ограниченную линией 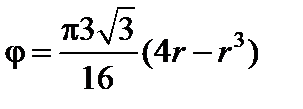, и осью Ox .

 

Функция φ=4r - r³ (график показан на рис. 2.25, слайд «Площадь для поляных координат») имеет два интервала монотонности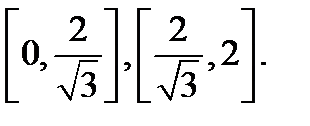  

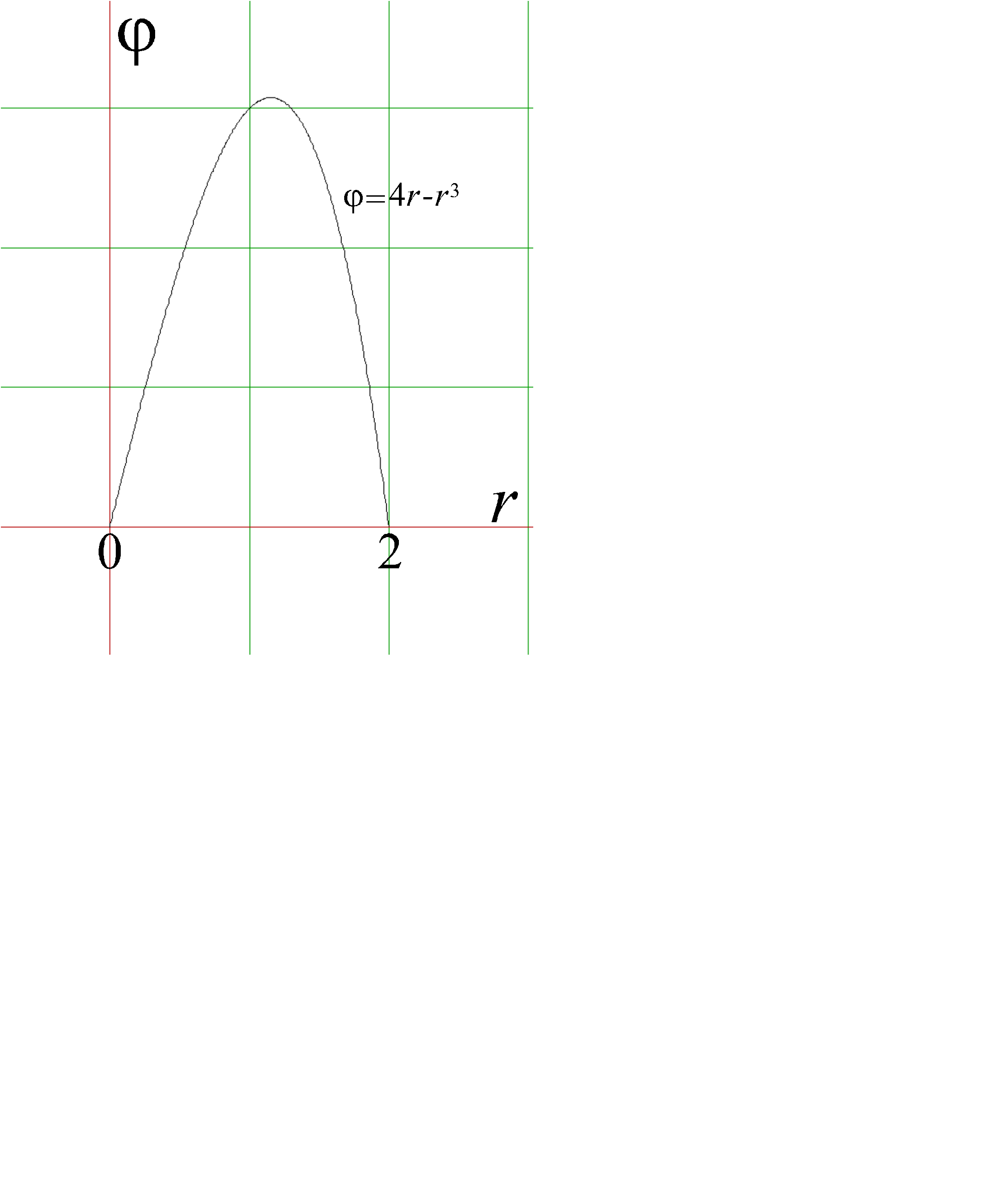
Рис. 2.25

Площадь для полярных координат

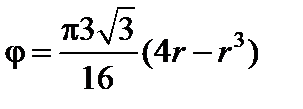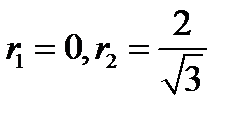 Максимум функции  равен  В нашем случае . Площадь искомой области

                                                                           .

 

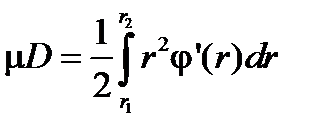
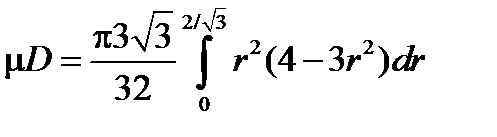
Пример. Найти площадь области ограниченную линией φ=r – sin r, и осью Ox. График фунции 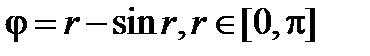 в декартовых координатах показан на рисунке 2.26, слайд «Площадь в полярных координатах»

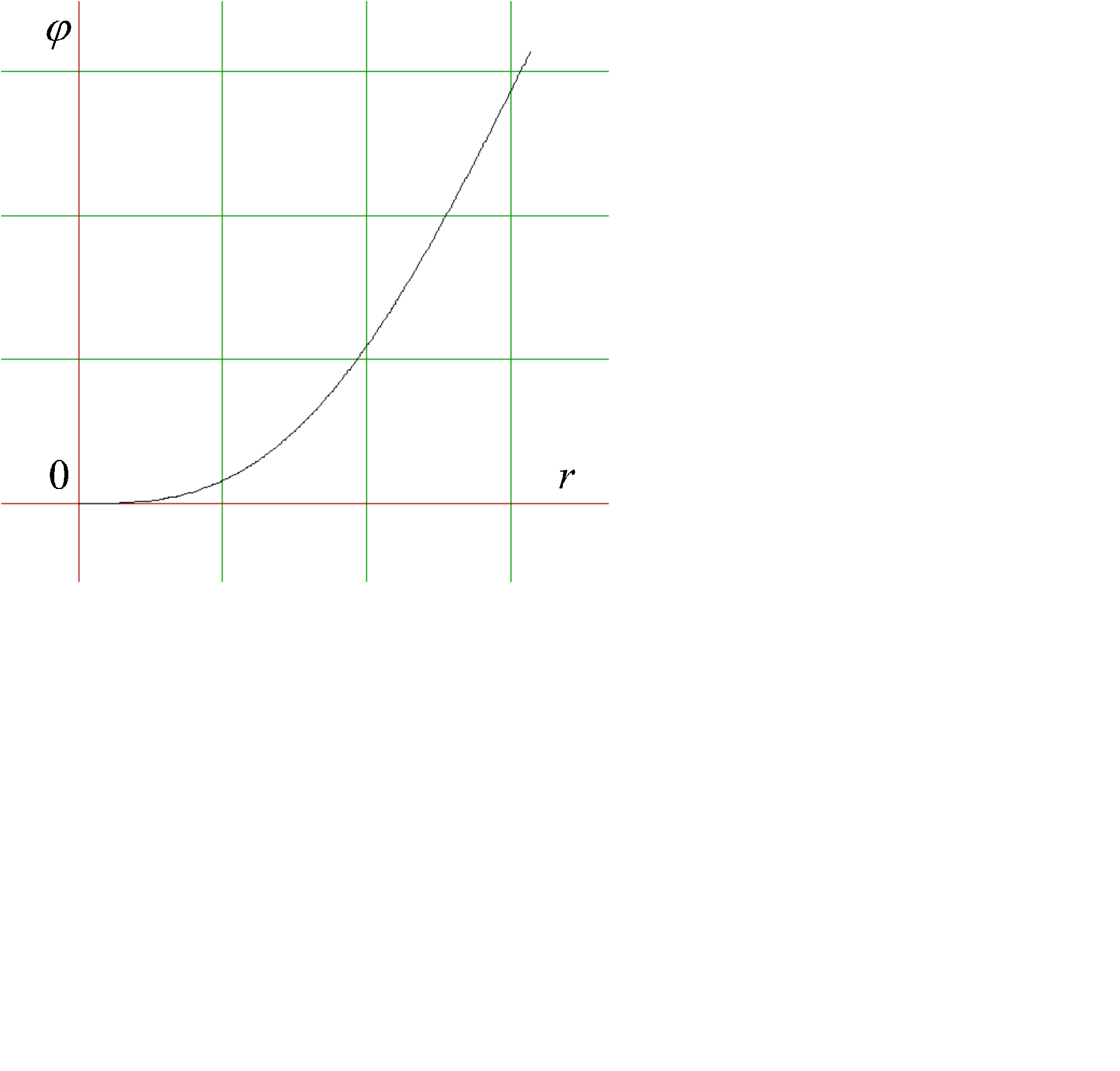
Рис. 2.26

 

Площадь в полярных координатах

                                                                               

Площадь области будет равна

 

                                                                                                                                                           

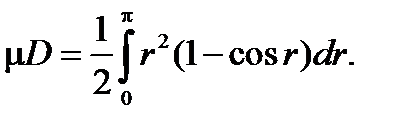
2.5. Вычисление объемов и площадей боковых поверхностей тел вращения

Объемы и площади поверхностей вращения. Теоремы Гюльдена.

 

Объем

Понятие объема вводится аналогично тому, как это делалось для площади, поэтому похожие моменты в этом параграфе будут излагаться конспективно. Известным считается понятие объема элементарной области, т.е. для области, ограниченной многогранником (сводится к объему тетраэдра, не обязательно правильного). В дальнейшем эту область так же будем называть многогранником. Объединение конечного числа непересекающихся многогранников также будет называться многогранником (рис. 2.27).

Рис. 2.27

Далее рассматривается класс пространственных областей, которые ограничены (содержаться в некотором шаре) и для которых существует хотя бы один вписанный многогранник. Вписанные многогранники будем обозначать P_i описанные P_e . Объем обозначается mP. Объем обладает свойством монотонности, таким образом, всегда mP_i £ mP_e .

Нижний объем: mD = sup mP_i , где точная грань берется по всевозможным вписанным многогранникам.

Верхний объем: 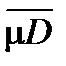= inf mP_e , где точная грань берется по всевозможным описанным многогранникам.

Аналогично тому, как это делалось площадей, доказывается неравенство  mD £ .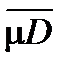

Определение. Область называется кубируемой, если совпадают нижний и верхний объемы 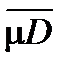= mD . Эта общая величина называется объемом и обозначается mD.

Теорема (Критерий кубируемости). Для того, чтобы область D была кубируемой необходимо и достаточно, чтобы "e>0$ P_e , P_i : mP_e - mP_i <e .

Теорема (Второй критерий кубируемости). Для того, чтобы область D была кубируемой необходимо и достаточно, чтобы "e>0$ кубируемые области D_e , D_i (не обязательно многогранники) такие, что  mD_e - mD_i <e .

Для объема справедливы свойства монотонности, аддитивности.

Пример. Цилиндр является кубируемым телом, если в его основании лежит квадрируемая фигура и его объем равен Sh (рис. 2.28).

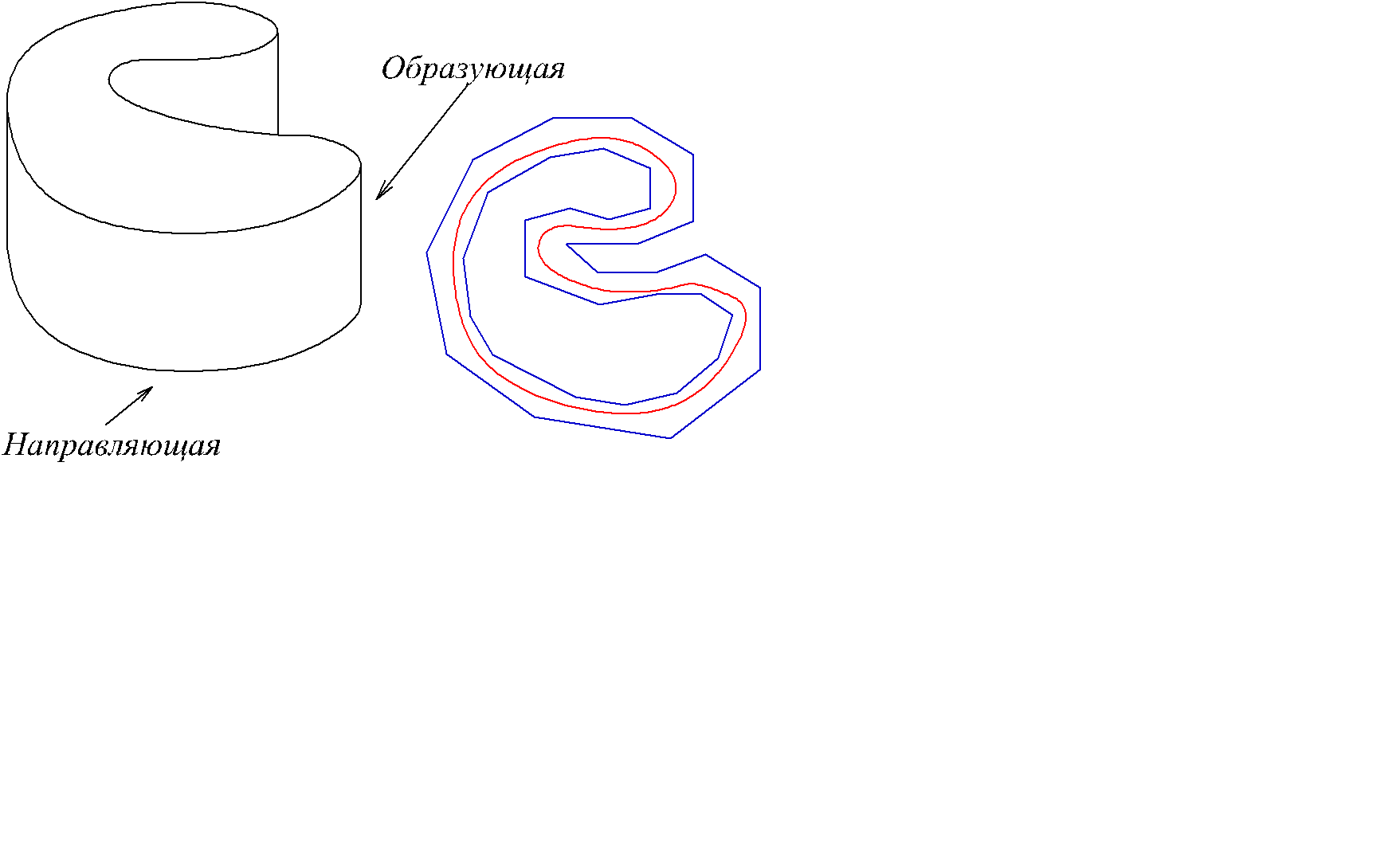
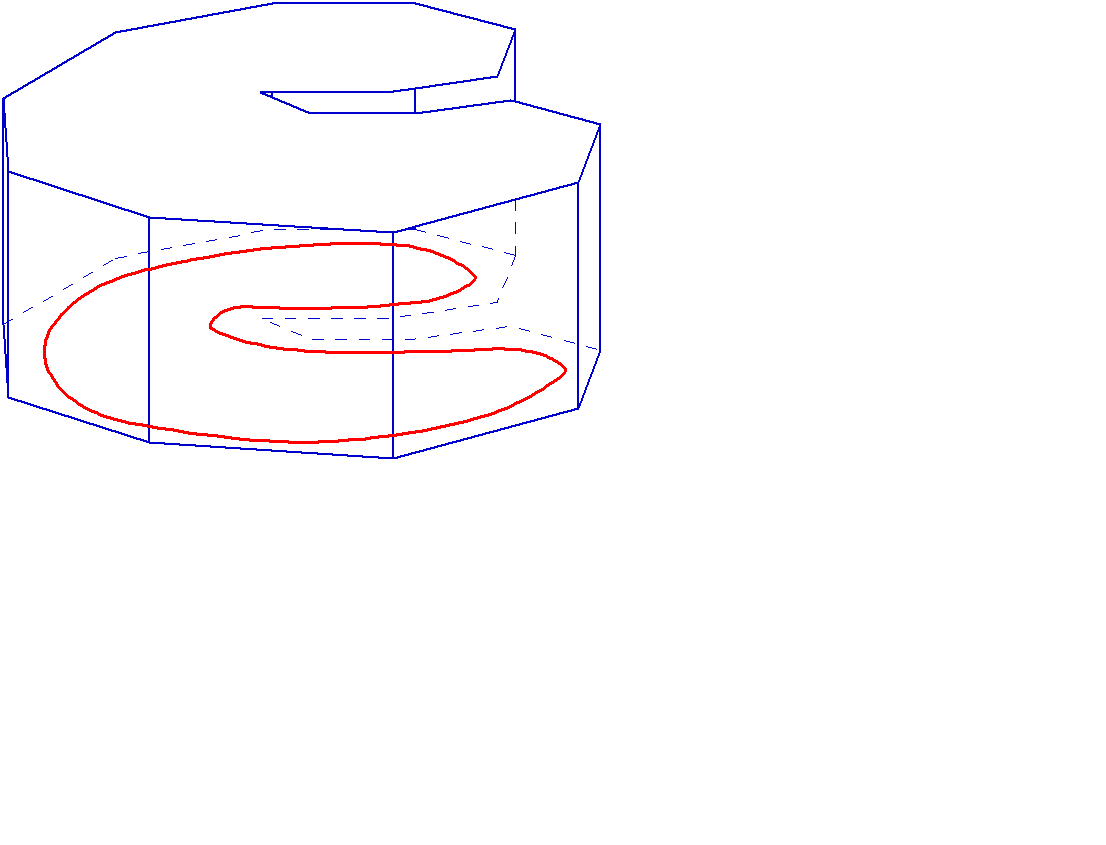
Рис. 2.28

Это следует из критерия кубируемости. В качестве вписанных и описанных многогранников выбираются призмы с той же образующей, что и у цилиндра, в основании которых лежат вписанные и описанные многоугольники для фигуры, лежащей в основании цилиндра.

В частности кубируемым будет «ступенчатое тело» (рис. 2.29), если в основании каждой составляющей лежит квадрируемая фигура.

Рис. 2.29

Объем тела вращения

Теорема. Если f(x)³ 0 непрерывна на [a , b] , то тело, граница которого, полученна вращением графика функции вокруг оси x (рис. 2.30, слайд «Тело вращения»), кубируемо и его объем равен

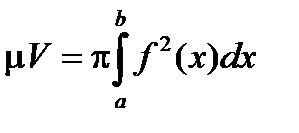
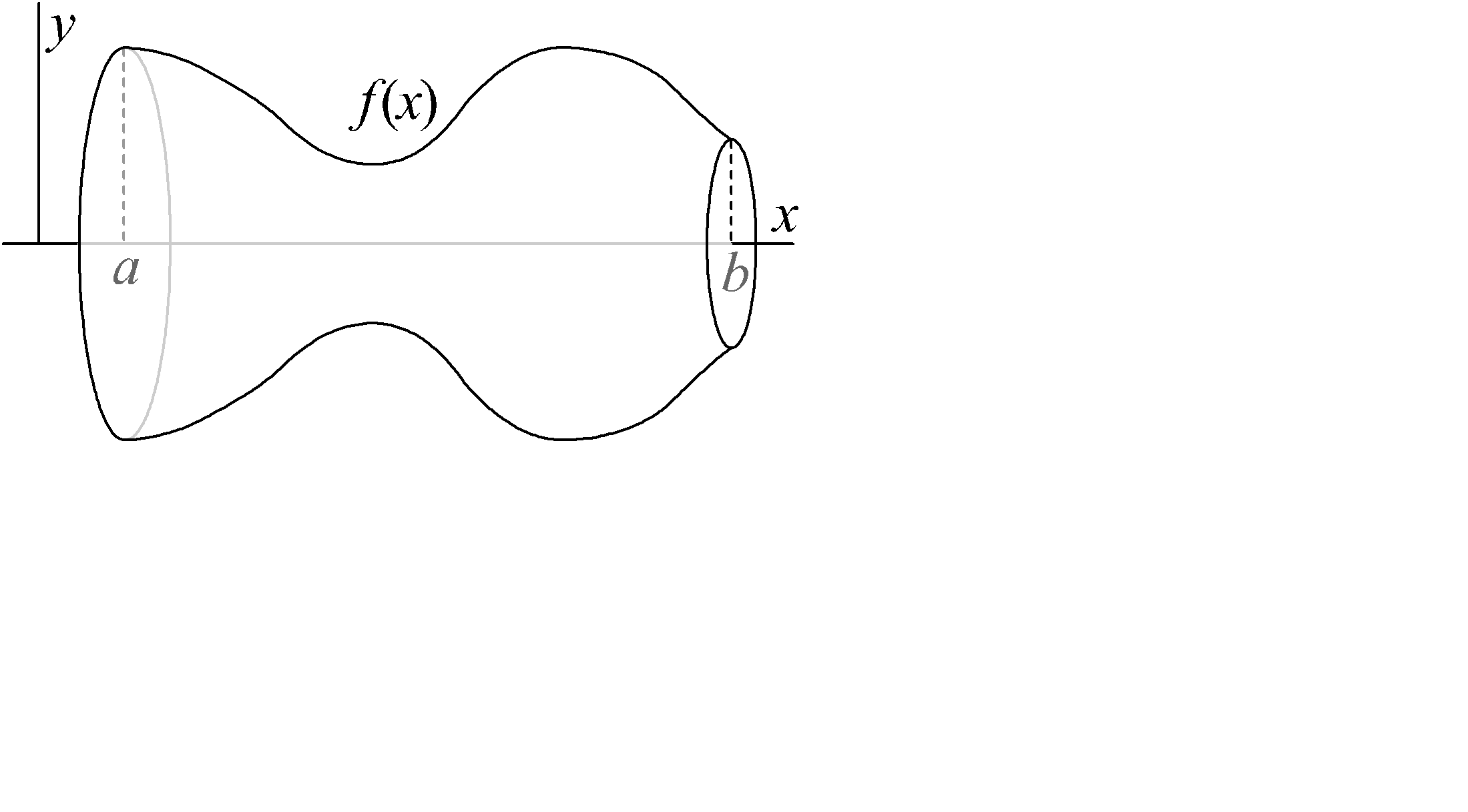
Рис. 2.30

Тело вращения

Доказательство. Для заданного e рассмотрим достаточно мелкое разбиение D={a = x₀< x₁<…< x_n = b} и два ступенчатых тела на основании сумм Дарбу исходной функции, составленных из круговых цилиндров высотой  x_{k +1} - x_k и радиусов   m_k = ,      M_k =  (Рис. 2.31). Объем этих тел будут равны s(F ,D), S(F ,D), где F(x)=p f ²(x) .

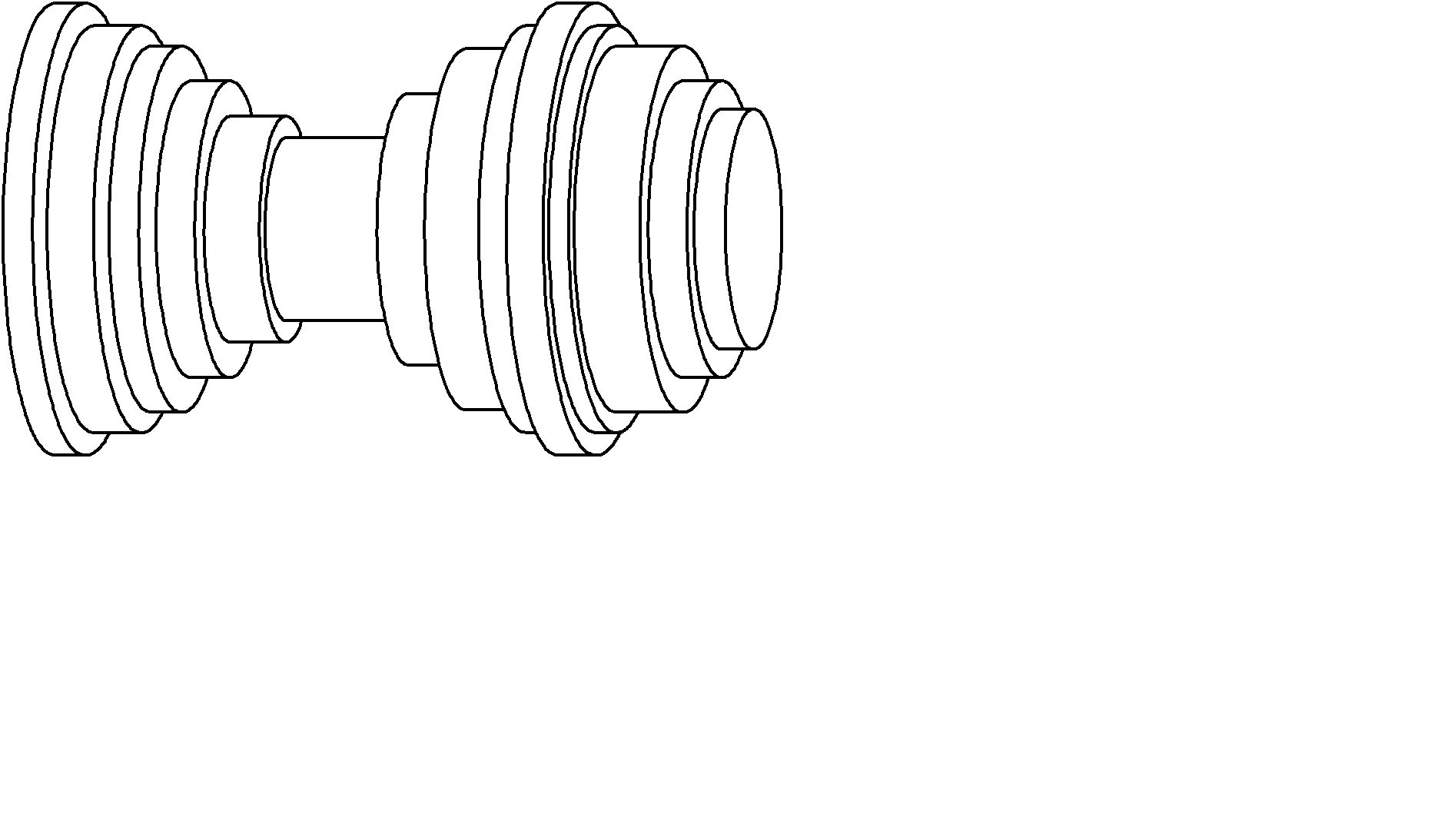
Рис. 2.31

Одна из этих кубируемых областей будет вписана в тело вращения, а другая описана. Разность объемов можно сделать сколь угодно малой, что следует из интегрируемости функции F(x).

Справедлива более общая теорема (без доказательства).

Теорема. Если область D проектируется на отрезок [a , b] оси x и любое сечение этой области плоскостью перпендикулярной оси x квадрируемо (рис. 2.32), а площадь этого сечения S(x) является интегрируемой функцией, то исходная область кубируема и ее объем равен

mD =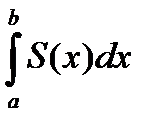

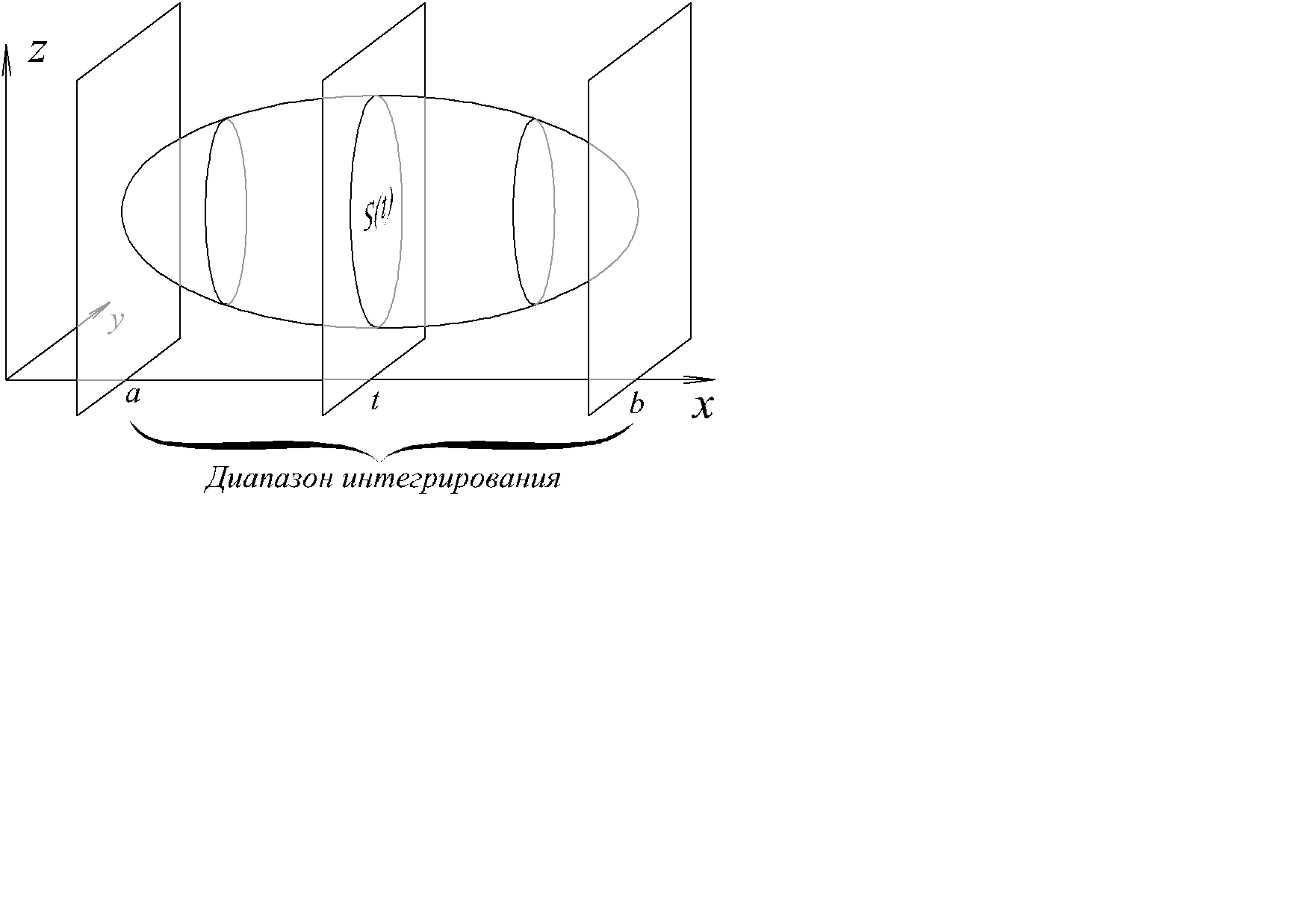
Рис. 2.32