Теорема 1 (первая теорема о среднем, см. слайд «Теорема о среднем»). Если m £ f(x) £ M на [a , b], то $ mÎ[m , M] такая, что
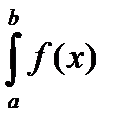 dx = m (b – a).
dx = m (b – a).
Теорема о среднем
Доказательство. ( a < b )
m(b - a)=  m dx £
m dx £  f(x) dx £
f(x) dx £  M dx = M(b – a). Откуда следует
M dx = M(b – a). Откуда следует
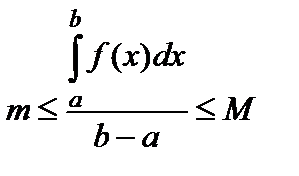 и m=
и m= 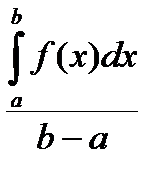 .
.
Следствие. Если f непрерывна, то $xÎ[a , b]:
 f(x) dx = f(x) (b – a).
f(x) dx = f(x) (b – a).
Для доказательства нужно взять 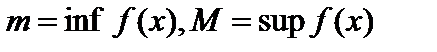 и воспользоваться теоремой о промежуточных значениях непрерывной функции.
и воспользоваться теоремой о промежуточных значениях непрерывной функции.
Теорема 2 (вторая теорема о среднем). Если m £ f(x) £ M на [a , b], f(x), g(x) интегрируемы и g(x) постоянного знака на [a , b] , то $ mÎ[m , M] :
 f(x)g(x) dx =m
f(x)g(x) dx =m  g(x) dx. (2.2)
g(x) dx. (2.2)
Доказательство. Пусть g(x)³ 0. Тогда
m g(x) £ f(x)g(x) £ M g(x), откуда
m 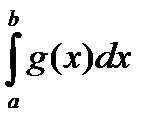 £
£  f(x)g(x) dx £ M
f(x)g(x) dx £ M  (2.3)
(2.3)
Если  g(x) dx =0, то из (2.3) следует, что
g(x) dx =0, то из (2.3) следует, что  f(x)g(x) dx =0 и соотношение (2.2) будет выполнено при m=0. Если
f(x)g(x) dx =0 и соотношение (2.2) будет выполнено при m=0. Если 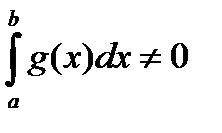 , то поделив выражения в (2.3) на
, то поделив выражения в (2.3) на  g(x) dx , получим требуемое соотношение, выбрав в качестве m число
g(x) dx , получим требуемое соотношение, выбрав в качестве m число  f(x)g(x) dx /
f(x)g(x) dx /  g(x) dx .
g(x) dx .
Если g(x)<0, то следует рассмотреть функцию G(x)=-g(x).
Теорема 3. Если f(x) – интегрируема на [a , b] и cÎ [a , b], то f(x) – интегрируема на [a , c] и [c , b] и (см. слайд «Аддитивность интеграла по множеству»)
 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(x) dx .
f(x) dx .
Аддитивность интеграла по множеству
Доказательство. Пусть D1 - разбиение [a , c]. Дополним это разбиение до разбиения D всего отрезка так, чтобы характеристика разбиения не изменилась l(D) = l(D1). В этом случае S(f,D1) – s(f,D1) £ S(f ,D) – s(f ,D) , откуда следует интегрируемость на отрезке [a , c]. Аналогично доказывается интегрируемость на отрезке [c , b] . Если существование интегралов доказано, то для доказательства требуемого равенства следует выбрать стандартные последовательности интегральных сумм s(f , 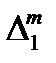 ,x'm ), s( f ,
,x'm ), s( f , 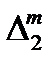 ,x''m ) для отрезков [a , c] и [c , b]. Возмем разбиение
,x''m ) для отрезков [a , c] и [c , b]. Возмем разбиение 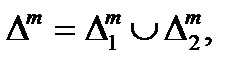 соствавленное из узлов разбиений
соствавленное из узлов разбиений 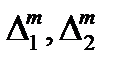 с теми же промежуточными точками xm =x'm
с теми же промежуточными точками xm =x'm  x''m . Для таких сумм получим (рис. 2.8)
x''m . Для таких сумм получим (рис. 2.8)
s( f,Dm ,xm) = s( f,  ,x'm) + s( f,
,x'm) + s( f,  ,x''m).
,x''m).
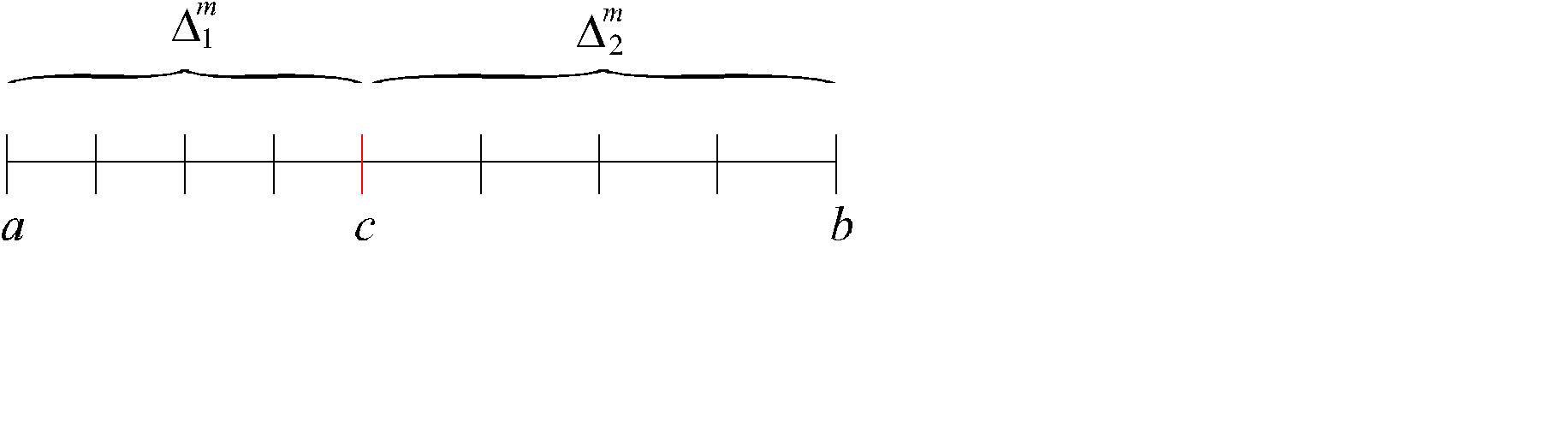
Рис. 2.8 (m=4)
Переходя к пределу при m®¥ получим требуемое соотношение.
Следствие. Для любых a , b , c справедливо равенство
 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(x) dx ,
f(x) dx ,
если указанные интегралы существуют.
Докажем это , например, для случая c < a < b .
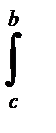 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx + 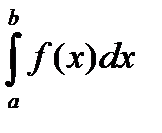 или
или 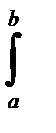 f(x) d = –
f(x) d = – 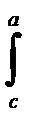 f(x) dx +
f(x) dx + 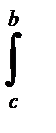 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx + 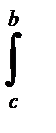 f(x) dx .
f(x) dx .
В качестве еще одного следствия можно получить следующую теорему
Теорема 4. (Непрерывность интеграла как функции верхнего предела). Если f интегрируема на [a,b], то функция F(x) = 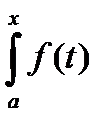 dt непрерывна на [a,b].
dt непрерывна на [a,b].
Доказательство.
|F(x+Dx) – F(x)| = 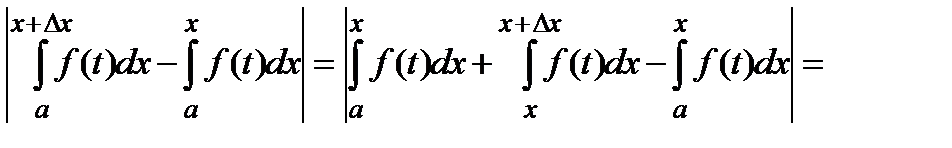 |
| 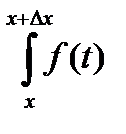 dt| £ M |Dx|.
dt| £ M |Dx|.
Теорема 5 (третья теорема о среднем). Если g(x) – монотонна и ограничена на [a , b], f(x) – интегрируема, то существует x такое, что
 f(x)g(x) dx = g(a)
f(x)g(x) dx = g(a) 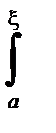 f(x) dx + g(b)
f(x) dx + g(b)  f(x) dx .
f(x) dx .
Доказательство (Для случая 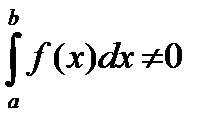 , f ( x )³0).
, f ( x )³0).
Вначале отметим, что справедливы следующие утверждения
Лемма 1. Любую точку m отрезка [A , B] можно единственным образом представить в виде m=aA +bB, где a³0, b³0, a + b = 1.
Действительно, если положить 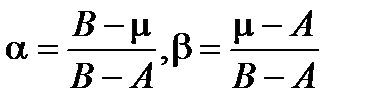 , то
, то 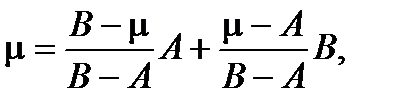 и a³0, b³0, a + b = 1. Наоборот, если m=aA +bB =aA+(1-a)B , то B - m=a(B - A) и
и a³0, b³0, a + b = 1. Наоборот, если m=aA +bB =aA+(1-a)B , то B - m=a(B - A) и  ,
, 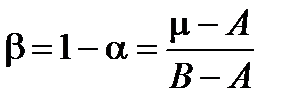 .
.
Числа a, b , удовлетворяющие указанным условиям, называются барицентрическими координатами точки m отрезка [A , B].
Лемма 2. Если f(x) интегрируема на [a , b] , 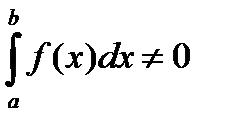 , то для любого
, то для любого  существует xÎ[a , b] такое, что числа
существует xÎ[a , b] такое, что числа 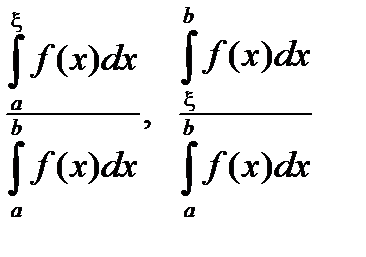 будут барицентрическими координатами числа
будут барицентрическими координатами числа 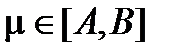 .
.
По лемме 1 будет m=aA +bB, где a³0, b³0, a + b = 1. Рассмотрим функцию 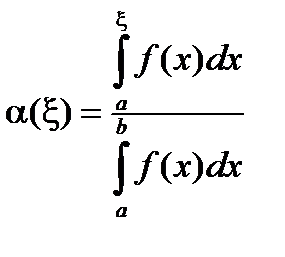 . Эта функция непрерывна и для нее a(a)=0, a(b)=1. По теореме о промежуточных значениях непрерывной функции найдется xÎ[a , b] такое, что a(x)=a . Тогда будет выполнено
. Эта функция непрерывна и для нее a(a)=0, a(b)=1. По теореме о промежуточных значениях непрерывной функции найдется xÎ[a , b] такое, что a(x)=a . Тогда будет выполнено
1-a(x)=1 – 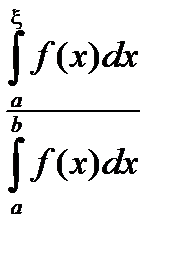 =
= 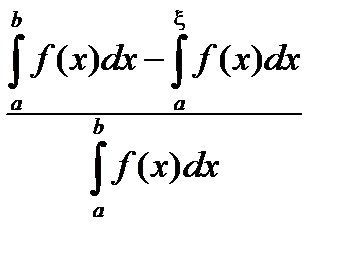 =
=  . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание. Можно было в качестве a(x) взять функцию a(x)=  , b(x)=
, b(x)=  , a(a)=1, a(b)=0. В этом случае
, a(a)=1, a(b)=0. В этом случае
 f(x)g(x) dx = g(a)
f(x)g(x) dx = g(a) 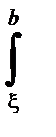 f(x) dx + g(b)
f(x) dx + g(b) 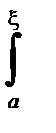 f(x) dx .
f(x) dx .
Доказательство теоремы. Сначала докажем теорему при дополнительном условии g(x) – монотонно возрастает. Из неравенств g(a)f(x) £ g(x)f(x) £ g(b)f(x) (у нас 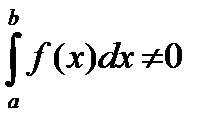 , f ( x )³0)) следует
, f ( x )³0)) следует
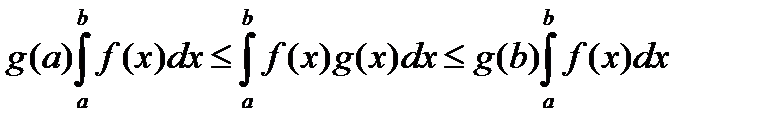 ,
,
откуда получим
 .
.
Таким образом, число m =  Î[g(a), g(b)]. По лемме 2 найдется x такое, что
Î[g(a), g(b)]. По лемме 2 найдется x такое, что
 =
= 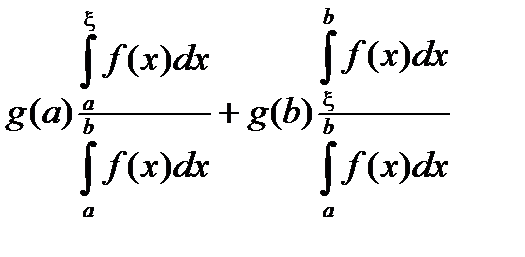 или
или
 f(x)g(x) dx = g(a)
f(x)g(x) dx = g(a) 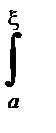 f(x) dx + g(b)
f(x) dx + g(b) 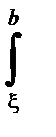 f(x) dx
f(x) dx
Если функция монотонно убывает, то следует рассмотреть функцию G(x) = – g(x) , которая будет монотонно возрастать и для неё воспользуемся доказанным утверждением
 f(x)G(x) dx =G(a)
f(x)G(x) dx =G(a)  f(x) dx+G(b)
f(x) dx+G(b)  f(x) dx, или
f(x) dx, или
–  f(x)g(x) dx = –g(a)
f(x)g(x) dx = –g(a)  f(x) dx – g(b)
f(x) dx – g(b)  f(x) dx
f(x) dx
откуда и следует утверждение для функции g(x) .
Теорема 6 (Неравенство Коши-Буняковского). Если f(x), g(x) – интегрируемы на [a , b], то
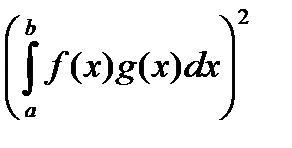 £
£  f 2 ( x ) dx
f 2 ( x ) dx 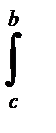 g 2 ( x ) dx или
g 2 ( x ) dx или
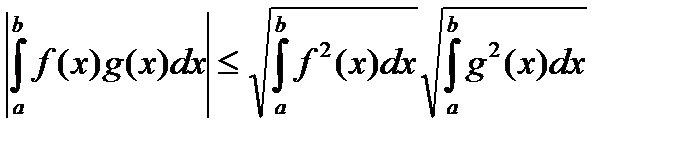 .
.
Доказательство. В силу свойств интеграла будут интегрируемы функции (f +lg)2, f 2, g2, тогда
0 £  (f+lg)2 dx=
(f+lg)2 dx=  f 2dx + 2l
f 2dx + 2l  f g dx +l2
f g dx +l2  g 2 dx =Al2+2Bl+C.
g 2 dx =Al2+2Bl+C.
Дискриминант будет  £ 0 откуда и следует неравенство Коши-Буняковского .
£ 0 откуда и следует неравенство Коши-Буняковского .
2.3. Определенный интеграл, как функция верхнего предела, вычисление определенных интегралов
Определенный интеграл, как функция верхнего предала. Замена переменных в определенном интеграле, интегрирование по частям. Длина дуги.
2.3.1. Производная интеграла по верхнему пределу
Отметим, что ранее была доказана
Теорема 1. Если f интегрируема на [a,b], то F(x) = 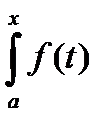 dt непрерывна на [a,b].
dt непрерывна на [a,b].
Теорема 2. Если f непрерывна на [a,b], то F(x) = 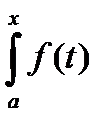 dt дифференцируема на [a,b] и F¢(x) = f(x).
dt дифференцируема на [a,b] и F¢(x) = f(x).
Доказательство.
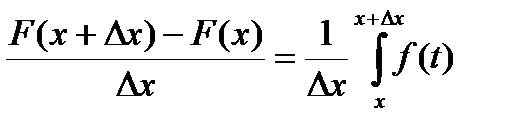 dt = f(x), где xÎ[x, x+Dx] при Dx >0 или xÎ[x+Dx, x] при Dx<0.
dt = f(x), где xÎ[x, x+Dx] при Dx >0 или xÎ[x+Dx, x] при Dx<0.
Следствие. Всякая непрерывная на [a,b] функция f(x) имеет на [a,b] первообразную
 dx =
dx = 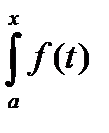 dt + C. (*)
dt + C. (*)
2.3.2. Формула Ньютона-Лейбница
Теорема. Если интегрируемая на [a,b] функция f имеет там первообразную F(x), то
 dx = F(b) – F(a) =
dx = F(b) – F(a) =  .
.
Доказательство. F(b) – F(a)= 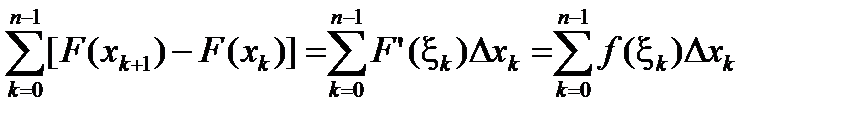 ®
® 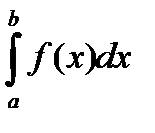 .
.
Замечание. Если f непрерывна, то формула Ньютона-Лейбница следует из (*).
2.3.3.Замена переменных в определенном интеграле
Теорема 1. Пусть f(x) непрерывна на [a,b], j(t) непрерывна вместе с производной на [a,b], причем j(t)Î[a,b], если tÎ[a,b], j(a)=a, j(b)=b. Тогда
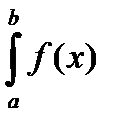 dx =
dx = 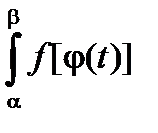 j¢(t) dt (2.4)
j¢(t) dt (2.4)
Формула (2.4) называется формулой замены переменного в определенном интеграле.
Доказательство. Оба интеграла в (2.4) существуют. Пусть F(x) первообразная функции f(x) , тогда F(j(t)) существует и является первообразной функции f(j(t))j¢(t). По формуле Ньютона-Лейбница
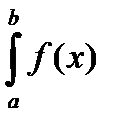 dx = F(b) – F(a),
dx = F(b) – F(a),  j¢(t) dt = F(j(b)) – F(j(a)) = F(b) – F(a).
j¢(t) dt = F(j(b)) – F(j(a)) = F(b) – F(a).
Замечание 1. Формула (2.4) иногда записывается в виде
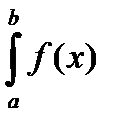 dx =
dx = 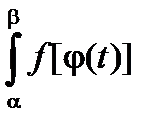 dj (t).
dj (t).
Замечание 2. Условия теоремы можно ослабить. От функции f(x) требуется интегрируемости и существования первообразной. Функция j(t) должна быть дифференцируема и должна существовать суперпозиция F(j(t)).
Интегрирование по частям
Теорема 2. Если функции u(x), v(x) непрерывны вместе со своими производными на [a , b], то
 dx =
dx =  –
– 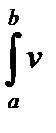 dx=
dx= 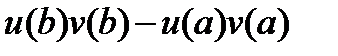 –
– 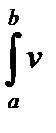 dx (2.5)
dx (2.5)
Доказательство.
 =
= 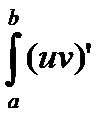 dx =
dx =  dx =
dx = 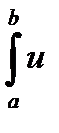 dv +
dv + 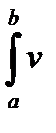 du .
du .
Откуда и следует формула (2.5).
Примеры


3.3. Вычислить  . Имеем
. Имеем 
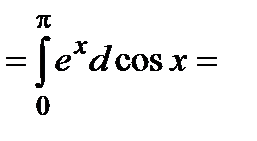
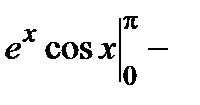
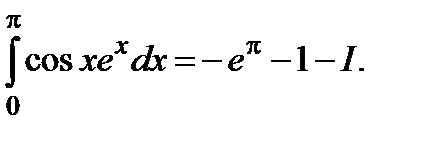 Откуда получим
Откуда получим 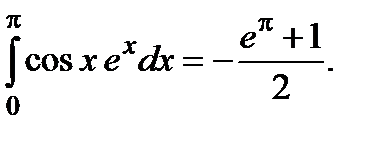
3.4. Вычислить 
 .
.

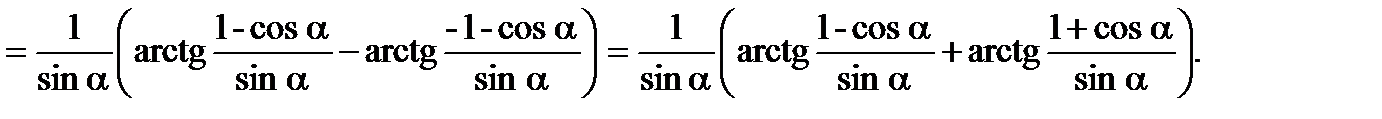
Если формально применить формулу  (в нашем случае 1-ab=0), то
(в нашем случае 1-ab=0), то 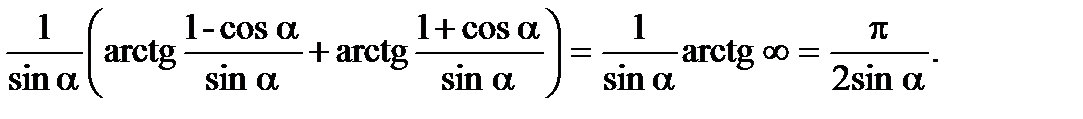 Законность этой операции можно обосновать.
Законность этой операции можно обосновать.
2.3.5. Остаточный член формулы Тейлора в интегральной форме
Пусть функция f(x) определена на отрезке [a , b] и имеет там непрерывные производные до порядка n +1. Тогда для всех x из [a , b] справедлива формула Тейлора с остатком в интегральной форме
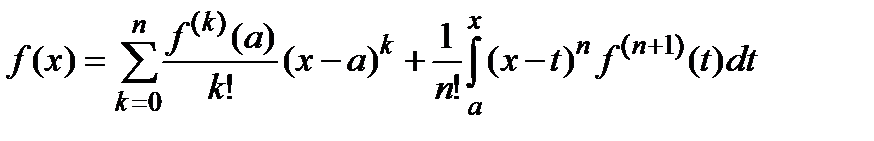 .
.
Доказательство. Обозначим остаток в формуле Тейлора Rn +1= 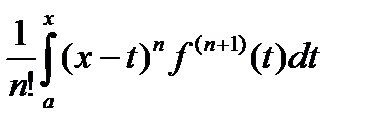 , Uk =
, Uk = 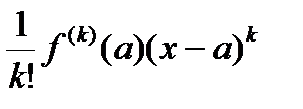 . Интегрируя по частям, получим
. Интегрируя по частям, получим
Rn+1= 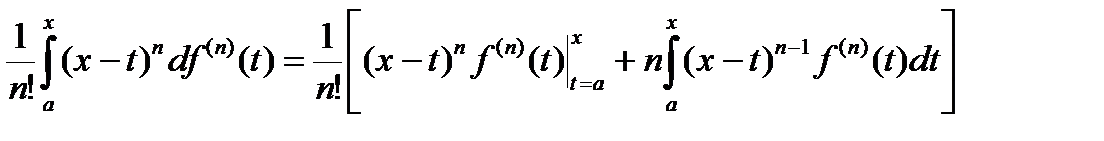 =
= 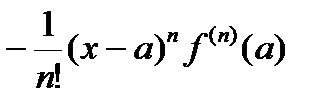 + Rn= =– Un+ Rn =– Un – Un-1+ Rn-1=…= –
+ Rn= =– Un+ Rn =– Un – Un-1+ Rn-1=…= –  + R1=
+ R1= 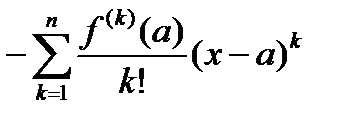 +
+ 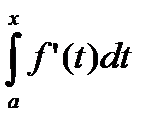 =
=  . Откуда и следует доказываемая формула.
. Откуда и следует доказываемая формула.
Длина дуги гладкой кривой
Ранее была доказана
Теорема. Если кривая
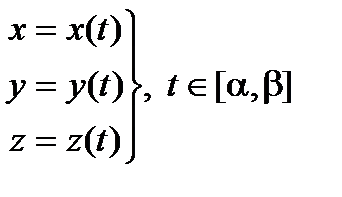
непрерывно дифференцируема, то длина ее дуги s(t) от начала кривой до точки с параметром t (рис. 2.9) является строго монотонно возрастающей, непрерывно дифференцируемой функцией и
 .
.
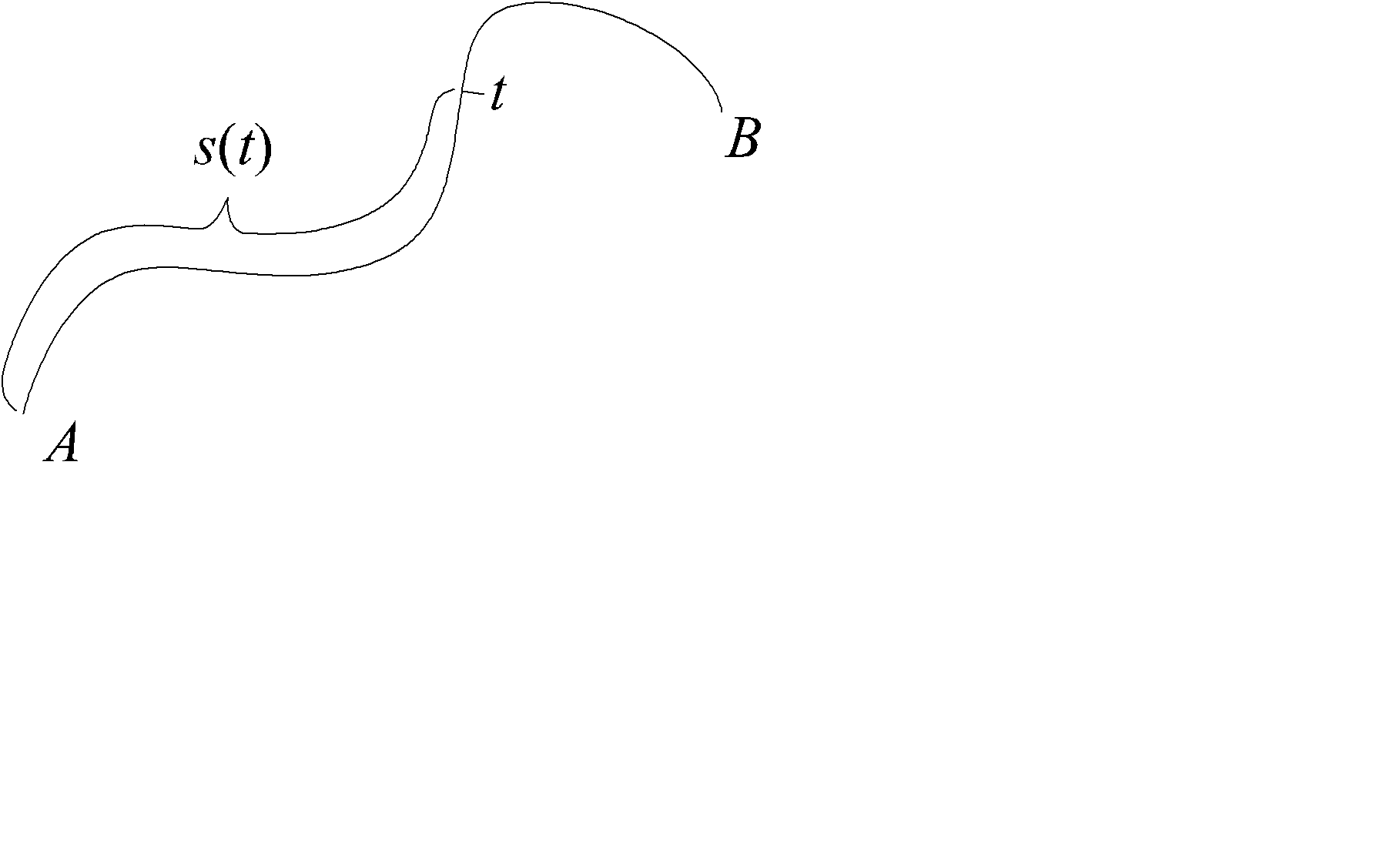
Рис. 2.9
Следствием является
Теорема. При условии непрерывной дифференцируемости длина кривой равна
s = 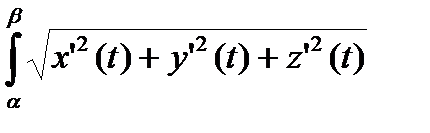 dt (2.6)
dt (2.6)

Рис. 2.10
Равенство (2.6) для длины кривой следует из предыдущей теоремы с помощью формулы Ньютона-Лейбница.
Замечание 1. В плоском случае
s =  dt .
dt .
Замечание 2. Если в качестве кривой рассматривается график функции f(x) на отрезке [a , b], то эту кривую можно параметризовать 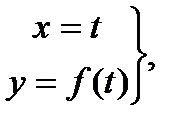 tÎ[a , b] и ее длина будет вычисляться по формуле s =
tÎ[a , b] и ее длина будет вычисляться по формуле s = 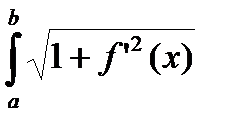 dx .
dx .
Рис. 2.11
Замечание 3. Для графика функции, заданной в полярных координатах r(j), jÎ[a,b] длина кривай будет равна
s =  dj.
dj.

Рис. 2.12
Для вывода этой формулы следует рассмотреть параметризацию кривой
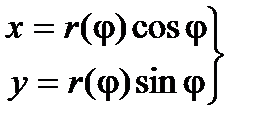 , jÎ[a,b].
, jÎ[a,b].
Примеры.
1.1. Вычислить длину кривой 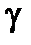 , y =ln cos x ,
, y =ln cos x ,  .
.
Длина кривой будет равна 
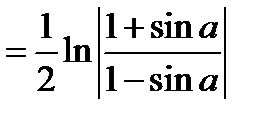 .
.
1.2. Вычислить длину астроиды x2/3+ y2/3= a2/3.(рис. 2.13, слайд «Астроида»)

Рис. 2.13
Астроида
В парметрическом виде уравнение астроиды имеет вид 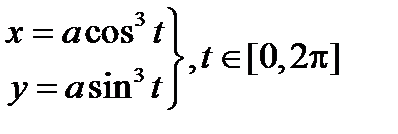 . Вычислим производные и подинтегральную функцию для нахождения длины дуги кривой, расположенной в первом квадранте :
. Вычислим производные и подинтегральную функцию для нахождения длины дуги кривой, расположенной в первом квадранте :
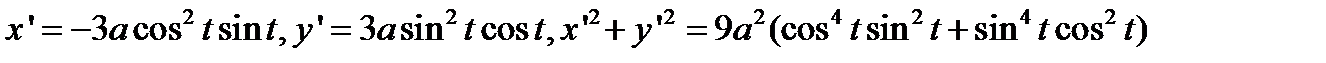 ,
, 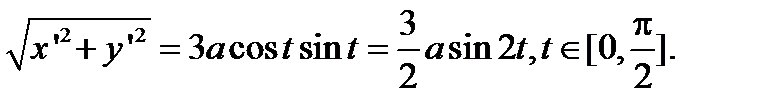 Длина всей дуги будет равна
Длина всей дуги будет равна
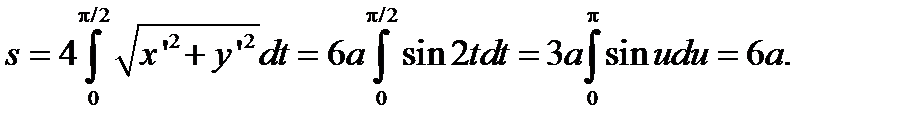

 2.4. Площадь плоской области
2.4. Площадь плоской области
Квадрируемость. Криволинейна трапеция. Области с границей в полярных координатах
Квадрируемые фигуры
Многоугольником P в этом параграфе называется внутренняя часть области, ограниченной замкнутой не самопересекающейся ломаной L . Для упрощения формулировок, объединение конечного числа многоугольников будет также называться многоугольником (см рис. 2.14).
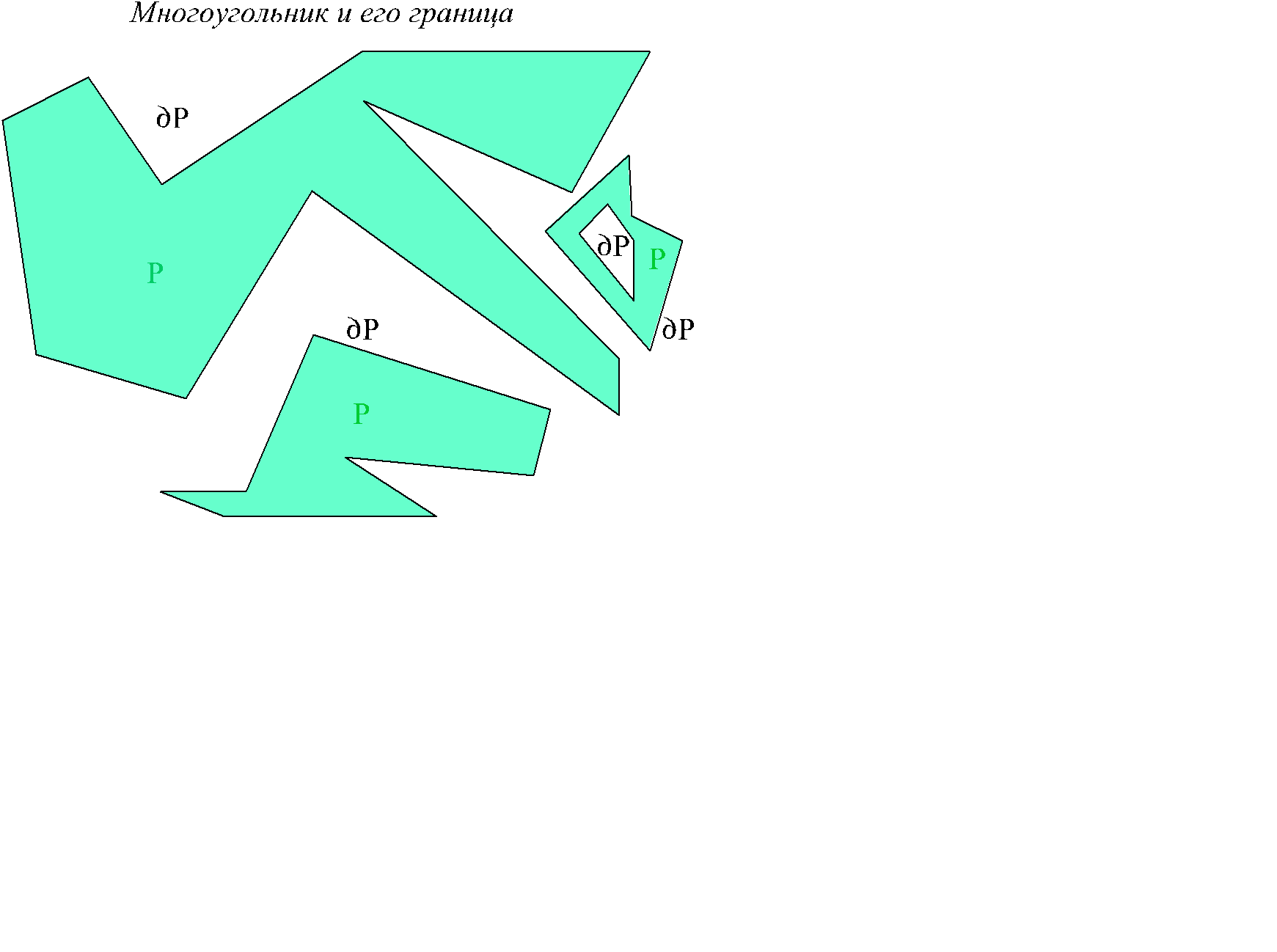
Рис. 2.14
Сама ломаная L (или ломаные) называется границей многоугольника P и обозначается ¶P . Многоугольник плюс граница обозначается  = P +¶P (замыкание области). Для области, показанной на рисунке, граница состоит из двух замкнутых ломаных. Будем предполагать известным понятие площади для многоугольников (эта площадь находится триангуляцией, разбиением области на треугольники Рис. 2.15).
= P +¶P (замыкание области). Для области, показанной на рисунке, граница состоит из двух замкнутых ломаных. Будем предполагать известным понятие площади для многоугольников (эта площадь находится триангуляцией, разбиением области на треугольники Рис. 2.15).
Рис. 2.15
Под областью в этом параграфе будем понимать ограниченное множество, для которого существует хотя бы один вписанный многоугольник. Кроме того, мы в дальнейшем будем рассматривать только множества, ограниченные одной или несколькими замкнутыми кривыми.
Определение. Индексом i будем обозначать многоугольники, вписанные в заданную область D , Pi Ì Dȶ D ( ¶ D – кривая, ограничивающая область D ). Индексом e будем обозначать описанные многоугольники, Pe É Dȶ D . Площадь многоугольника P будем обозначать через mP (см. слайд «Вписанные и описанные многоугольники»).
Вписанные и описанные многоугольники
Для площади многоугольников известно свойство монотонности: если PÌQ , то mP £ mQ .
Определение. Нижней площадью области D назовем величину mD = sup mPi , где точная верхняя грань берется по всевозможным вписанным многоугольникам.
Верхней площадью области D назовем величину  = inf mPe , где точная нижняя грань берется по всевозможным описанным многоугольникам.
= inf mPe , где точная нижняя грань берется по всевозможным описанным многоугольникам.
Как уже отмечалось, мы будем рассматривать лишь ограниченные области, для которых множество вписанных многоугольников не пусто. В этом случае верхние и нижние площади будут существовать.
Лемма. mD £ 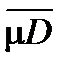 .
.
Доказательство. От противного. Пусть 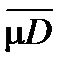 £ mD (см. слайд «Неравенство между нижней и верхней площадью»).
£ mD (см. слайд «Неравенство между нижней и верхней площадью»).
Неравенство между нижней и верхней площадью
Выбираем непересекающиеся окрестности чисел  , mD . По определению нижней и верхней площадей найдутся два многоугольника Pi , Pe , один с площадью mPe из выбранной окрестности числа
, mD . По определению нижней и верхней площадей найдутся два многоугольника Pi , Pe , один с площадью mPe из выбранной окрестности числа 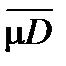 , другой с площадью из окрестности числа mD . Согласно выбору окрестностей mPe < mPi , что противоречит свойству монотонности площадей для многоугольников.
, другой с площадью из окрестности числа mD . Согласно выбору окрестностей mPe < mPi , что противоречит свойству монотонности площадей для многоугольников.
Следствие. Для любых Pi , Pe выполняется mPi £ mD £ 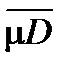 £ mPe .
£ mPe .
Определение. Область D называется квадрируемой, если 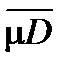 = mD . Эта общая величина называется площадью и обозначается mD .
= mD . Эта общая величина называется площадью и обозначается mD .
Теорема (критерий квадрируемости). Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы для любого e>0 существуют два многоугольника (описанный и вписанный) Pe , Pi такие, что mPe - mPi <e .
Доказательство. Как уже отмечалось для любых Pe , Pi выполняются неравенства
mPi £ mD £ 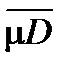 £ mPe ,
£ mPe ,
откуда и следует требуемое утверждение.
Следствие . Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы существовали две последовательности многоугольников 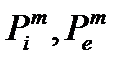 , такие, что
, такие, что  .
.
Замечание. Для многольников, указанных в этом следствии , справедливы равенства 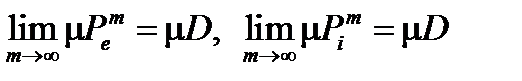 .
.
Определение. Множество D имеет площадь 0, если его можно покрыть многоугольниками со сколь угодно малой суммарной площадью.
Если область D имеет границу ¶D, то для квадрируемости D необходимо и достаточно, чтобы ¶D имела площадь равную нулю.
Если многоугольники Pe и Pi имеют разность площадей mPe - mPi < 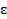 , то область Pe \Pi (полоса между ломаными, ограничивающими многоугольники Pe , Pi ) имеет площадь m (Pe \Pi )<
, то область Pe \Pi (полоса между ломаными, ограничивающими многоугольники Pe , Pi ) имеет площадь m (Pe \Pi )< 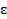 и содержит границу области D. Справедливо и обратное утверждение. Если многоугольник Q с площадью m (Q )<
и содержит границу области D. Справедливо и обратное утверждение. Если многоугольник Q с площадью m (Q )< 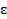 покрывает границу области D, то из его границ можно собрать границы двух многоугольников Pe и Pi с разностью площадей mPe - mPi <
покрывает границу области D, то из его границ можно собрать границы двух многоугольников Pe и Pi с разностью площадей mPe - mPi < 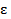 (без доказательства).
(без доказательства).
Свойства площади
Теорема (Монотонность). Если D1, D2 квадрируемы и D1Ì D2 , то mD1 £ mD2 (см. слайд «Свойство монотонности площади»).
Свойство монотонности площади
Доказательство. Любой Pi для D1 является вписанным и для D2, поэтому mD1=sup mPi будет £ m D2 (для области D2 площадь находится как верхняя грань площадей вписанных многоугольников по большему множеству).
Теорема (Аддитивность). Если квадрируемая область D разбита кусочно-гладкой кривой на две подобласти D1 , D2 , то они квадрируемы и
mD = mD1 + mD2.
Доказательство (только для ломаной, разбивающей область на две части). Обозначения см. слайд «Обозначения».
Обозначения
Выполнены следующие соотношения
Pi¢¢È Pi¢= Pi , Pe¢¢È Pe¢= Pe (2.7)
По заданному e выберем Pi , Pe так, что m Pe - m Pi < e . Из (2.7) следует, что
mPi¢¢ + mPi¢= mPi , mPe¢¢+ mPe¢= mPe . Вычитая из второго равенства первое получим , (mPe¢¢ - mPi¢¢) + (mPe¢ - mPi¢)= mPe - mPi < e . Откуда получаем неравенства (mPe¢¢ - mPi¢¢) < e , (mPe¢ - mPi¢) < e . Таким образом, квадрируемость D1 , D2 доказана. Для доказательства равенства mD = mD1 + mD2 отметим, что любой вписанный в D многоугольник Pi разбивается секущей ломаной на два вписанных многоугольника Pi¢¢È Pi¢= Pi для D1 , D2 . Поэтому mD =sup mPi £ mD1 +mD2. Точно также любой описанный многоугольник Pe распадается на два описанныхPe¢¢ÈPe¢= Pe . Поэтому будет выполнено обратное неравенство
mD =inf mPe³ mD1 +mD2.
Откуда и следует требуемое равенство.
В качестве еще одного свойства площади отметим ее независимость от выбора системы координат.
Теорема (Второй критерий квадрируемости). Пусть D некоторая область. Если для
"e>0 $ кадрируемые 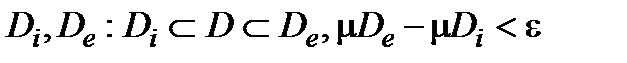 , то D квадрируема (см. слайд «Второй критерий квадрируемости»).
, то D квадрируема (см. слайд «Второй критерий квадрируемости»).
Второй критерий квадрируемости
В теореме сформулировано только достаточное условие квадрируемости, необходимость этого условия очевидна.
Доказательство. Возьмем 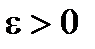 . Для него найдутся
. Для него найдутся  . В свою очередь для
. В свою очередь для 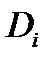 существует вписанный
существует вписанный 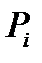 с такой площадью, что
с такой площадью, что 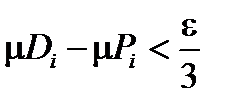 . Аналогично, для
. Аналогично, для  найдется описанный
найдется описанный 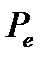 такой что
такой что  . Тогда
. Тогда
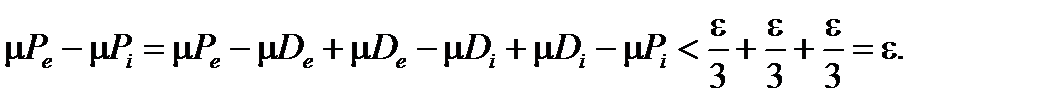
Так же как и для случая многоугольников, можно сформулировать
Следствие . Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы существовали две последовательности квадрируемых областей 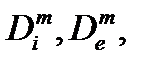 такие, что
такие, что 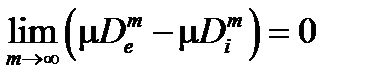 (см. слайд «Критерий квадрируемости в терминах границы»).
(см. слайд «Критерий квадрируемости в терминах границы»).
Критерий квадрируемости в терминах границы
2.4.3.Площадь криволинейной трапеции
Пусть f(x)³0 и непрерывна на отрезке [a , b]. Область расположенная между графиком функции f(x), осью x и вертикалями x = a , x = b называется криволинейной трапецией (см. слайд «Площадь криволинейной трапеции» ).
Площадь криволинейной трапеции
Теорема. Криволинейная трапеция D квадрируема и ее площадь
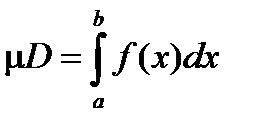 .
.
Доказательство. Пусть e>0. В силу интегрируемости f(x) для этого e существует разбиение отрезка [a , b], D={a = x0< x1<…< xn} такое, что S(f ,D) – s(f,D) < e . Прямоугольники, соответствующие нижней сумме Дарбу образуют вписанный в область D многоугольник Pi . Прямоугольники, соответствующие верхней сумме Дарбу образуют описанный многоугольник Pe для области D (Рис. 2.16), s(f ,D) = m Pi , S(f,D)= m Pe .
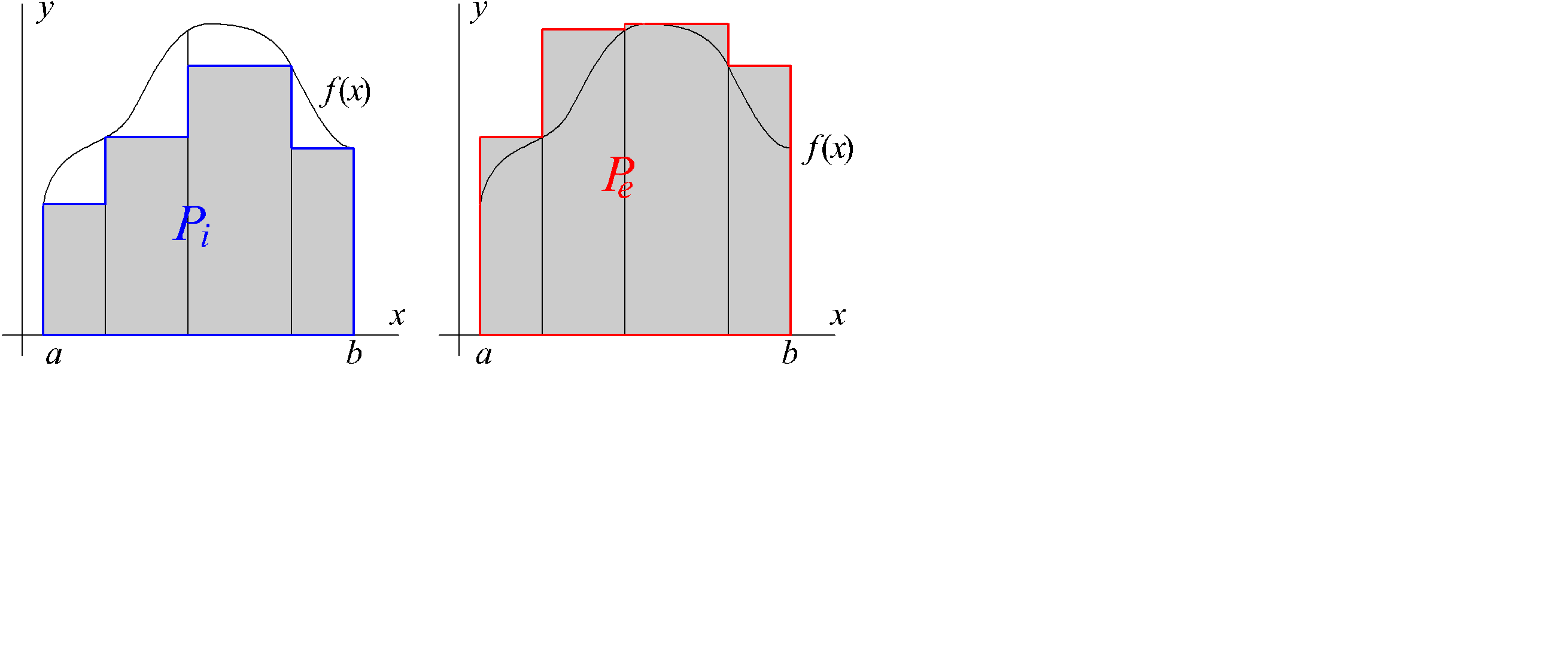
Рис. 2.16
Отсюда следует квадрируемость области D . Для доказательства равенства 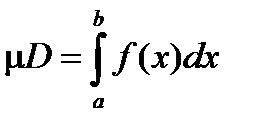 рассмотрим последовательность разбиений
рассмотрим последовательность разбиений  отрезка
отрезка  с равноотстоящими узлами. Соответствующие вписанные и описанные многоугольники обозначим
с равноотстоящими узлами. Соответствующие вписанные и описанные многоугольники обозначим  . Тогда, как уже упоминалось ранее, между суммами Дарбу и площадями многоугольников существует следующая связь
. Тогда, как уже упоминалось ранее, между суммами Дарбу и площадями многоугольников существует следующая связь 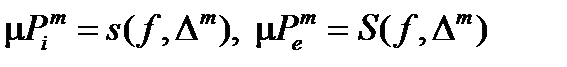 . Далее
. Далее  и
и 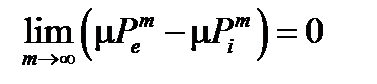 . Эти равенства позволяют утверждать (следствие из критерия интегрируемости), что
. Эти равенства позволяют утверждать (следствие из критерия интегрируемости), что 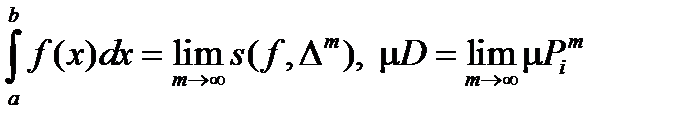 . Таким образом,
. Таким образом,  .
.
Замечание. Если f(x)£ 0 и непрерывна на отрезке [a , b], то 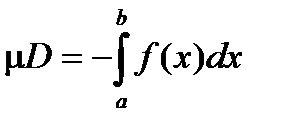 . Для области
. Для области
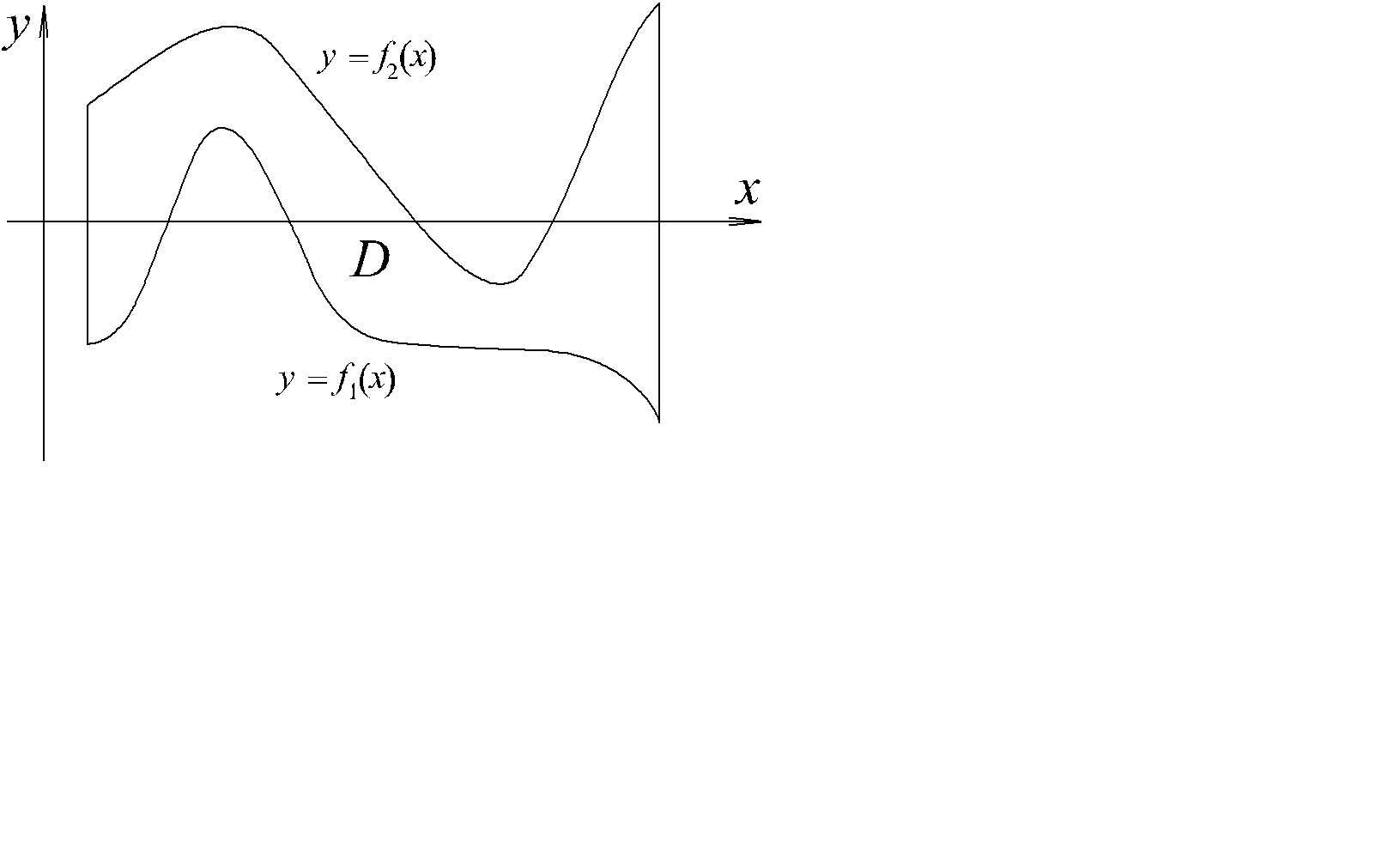
D , заключенной между двумя непрерывными кривыми (графиками функций) y = f1(x),
y=f2(x), f1(x)£ f2(x) на [a,b], 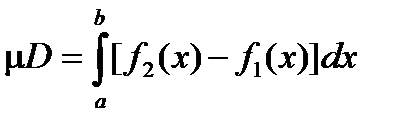 (рис 2.17).
(рис 2.17).

| 
|
| Рис. 2.17 | |
В более общих случаях для вычисления площади следует разбить область на фигуры указанного вида.
Дата: 2019-03-05, просмотров: 328.