Теоремы 2. Любая монотонная ограниченная функция является интегрируемой функцией.

  Доказательство. Пусть f  монотонно возрастает, тогда

S(f ,D) - s(f ,D) = 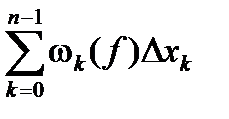 = = 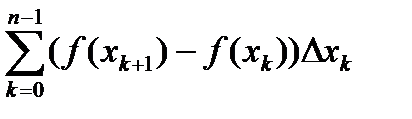<l(D) =

=l(D)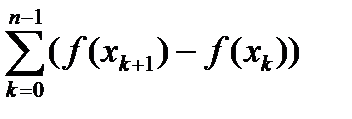(f(b) – f(a)), откуда и следует интегрируемость (по теореме Дарбу).

Теорема 3. Любая ограниченная функция, имеющая конечное число разрывов интегрируема.

  Доказательство. Пусть функция f(x) ограничена на [a , b], | f ( x )| £ M и имеет  p точек разрыва {u_k} . Для упрощения доказательства будем предполагать, что все точки разрыва внутренние. Пусть e > 0, рассмотрим непересекающиеся окрестности точек разрыва 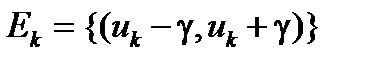   с суммарной длиной 2g p < e, будем также предполагать, что все  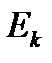лежат в интервале (a , b) (рис. 2.3). Функция f  равномерно непрерывна на дополнении 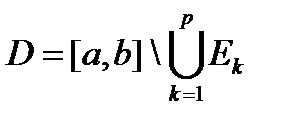, поэтому существует d > 0 такое, что | f(x¢¢)- f(x¢)|<e  при |. Возьмем разбиение D с характеристикой l(D)<min(d,e). В этом случае на отрезках , лежащих в D колебание функции будет w_k(f) < e . Представим разность сумм Дарбу S – s в виде трех сумм (рис. 2.3)

S – s = S w_k(f) D x_k =S¢ + S¢¢ + S¢¢¢ .

Через S¢  обозначена часть суммы S w_k(f) D x_k , для которой все [x_k , x_{k +1}]ÌD . Для нее будет выполнено неравенство S¢  = S¢ w_k(f) D x_k £ S¢ e D x_k = (b – a) e.

Через S¢¢  - обозначена часть суммы S w_k(f) D x_k , для которой [x_k , x_{k +1}]Ì 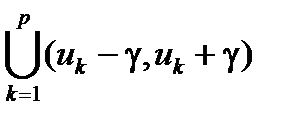. Для этой суммы S¢¢  £ S¢¢ 2M D x_k = 2M S¢¢ D x_k < 2M e (суммарная длина S¢¢ D x_k  меньше e).

Через S¢¢¢ обозначена часть суммы S w_k(f) D x_k , содержащая остальные слагаемые (таких слагаемых будет 2p).  Для этой суммы S¢¢¢  £ S¢¢¢ 2M D x_k = 2M S¢¢¢ D x_k < 2M 2p e .

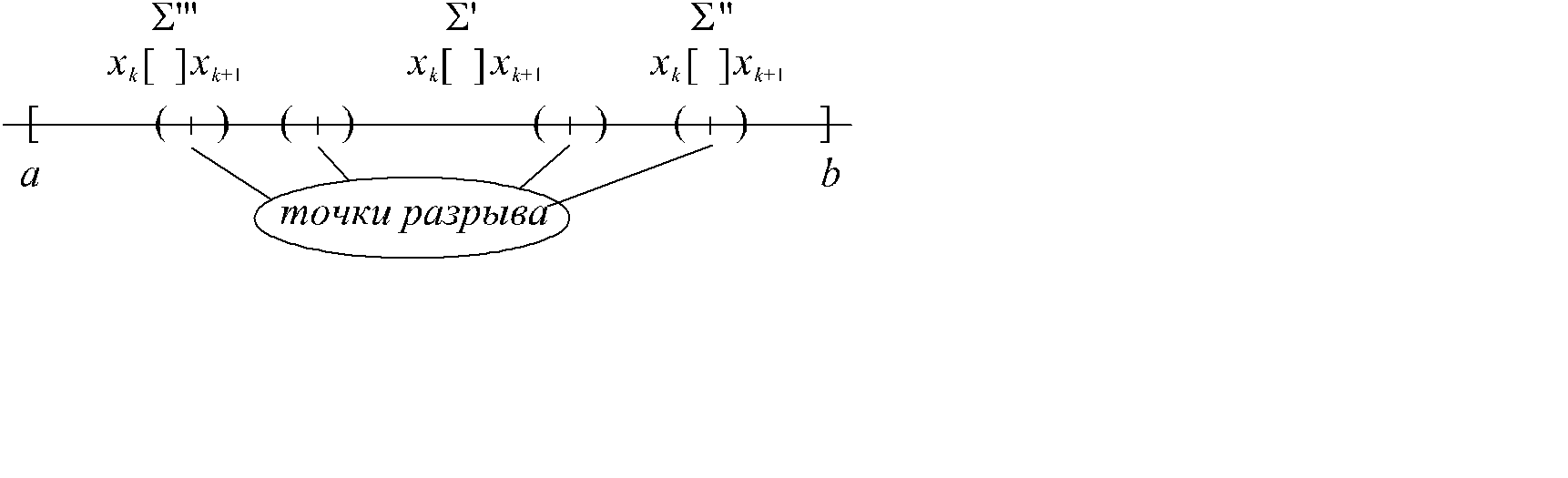
Рис. 2.6

  Таким образом, для разбиения с выбранной характеристикой l(D) справедливо неравенство S – s=S¢ + S¢¢ + S¢¢¢  < (b – a +2M +4Mp ) e. По теореме Дарбу функция интегрируема.

  Следствие. Изменение функции в конечном числе точек не влияет на интегрируемость (см. слайд «Изменение функции в конечном числе точек»).

  Теорема 4. Ограниченная, имеющая счетное число разрывов функция интегрируема.

Без доказательства.

Изменение функции в конечном числе точек

2.2.3. Свойства определенного интеграла

Во многих случаях в доказательствах будет использоваться теорема Дарбу. Именно, если окажется, что функция 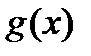интегрируема и для любого разбиения  выполнено неравенство 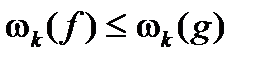 , то функция  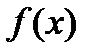также будет интегрируема. Действительно, в этом случае S(f ,D)– s(f ,D)=Sw_k(f) Dx_k £ Sw_k(g)Dx_k=S(g ,D)– s(g,D) и можно сослаться не теорему Дарбу.

1) Если f и g интегрируемы на [a,b], то f + g также интегрируема на [a,b] и

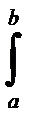(f(x) + g(x))dx = 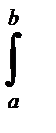f(x)dx + 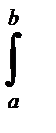g(x)dx.

Доказательство. Так как | f(x)+ g(x) – f(y) – g(y)| £ | f(x)– f(y) |+| g(x)– g(y)|, то для заданного разбиения  D будет выполнено неравенство

w_k (f + g) =sup| f(x)+ g(x) – f(y) – g(y)| £ sup(| f(x)– f(y) |+| g(x)– g(y)|)£ sup| f(x) - f(y)|+

+ sup|g(x) – g(y)|= w_k (f)+ w_k(g). Отсюда S(f+g ,D)–s(f+g ,D)=Sw_k(f+g) Dx_k £

£Sw_k(f)Dx_k +Sw_k(g)Dx_k= S(f ,D)– s(f ,D) +S(g ,D)–s(g,D).

Откуда следует интегрируемость суммы f + g. Далее для стандартной последовательности интегральных сумм

s^m(f + g) = s^m(f) + s^m(g).

Переходя к пределу при m ®¥ , получим требуемое равенство.

2) Если f  интегрируема на [a , b] , то cf(x) также интегрируема и

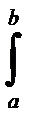c f(x)dx =c 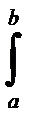f(x)dx.

Утверждение следует из соотношения s(cf ,D,x)= cs(f ,D,x) для интегральных сумм.

3) Если f  интегрируема на [a , b] , то | f(x)| также интегрируема и

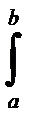| f(x)dx | £ 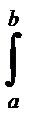| f(x)| dx .

Доказательство. Дано разбиение D. Тогда

w_k (| f |) =sup|| f(x)| –| f(y)||£ sup| f(x)– f(y) |= w_k(f) ,

S(|f | ,D) – s(|f | ,D)=Sw_k(|f |) Dx_k £ Sw_k(f) Dx_k = S(f ,D) – s(f ,D) .

Откуда следует интегрируемость | f |. Далее для стандартной последовательности интегральных сумм будет выполнено

|s^m(f)|£ s^m(| f |).

Переходя к пределу при m ®¥,  получим требуемое неравенство.

4) Если  f , g интегрируемы на [a , b] , то f(x)g(x) также интегрируема.

Доказательство. Так как функции интегрируемы, то они ограничены | f(x)| £ M , | g(x)| £ M . Выполнено соотношение

f(x)g(x) – f(y)g(y) = f(x)g(x) – f(x)g(y) + f(x)g(y) – f ( y)g(y) = f(x)(g(x) – g(y)) + g(y)( f(x) – f(y)).

 Тогда для заданного разбиения будет выполнено неравенство

w_k(fg) £ Mw_k(g) + Mw_k(f) и, следовательно, функция f(x)g(x) будет интегрируема.

5) Если g(x) – монотонна и ограничена на [a , b],  f(x) – интегрируема, то f(x)g(x) интегрируема.

Это непосредственное следствие из предыдущего свойства и интегрируемости монотонной, ограниченной функции.

6) Если  f отлична от 0 лишь в конечном числе точек, то она интегрируема и ее интеграл равен нулю.

Доказательство. Достаточно доказать для одной точки

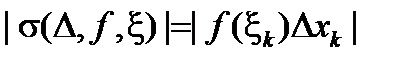 или 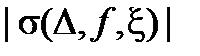=0, в зависимости от того, попадет единственная точка, где функция отлична от нуля, в число промежуточных точек или нет. Во всяком случае, всегда будет выполнено неравенство |s(f ,D,x)| £ Ml(D).

Рис. 2.7

Следствие. Если f₁ интегрируема, и  f₂ отлична от  f₁  на конечном числе точек, то f₂ также интегрируема и

=  .

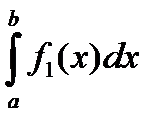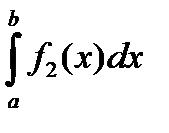Доказательство. f₂ = f₁ + ( f₂ – f₁ ).

7) 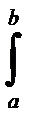1 dx = b – a.

8) Если a < b , то по определению полагают

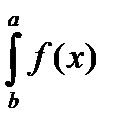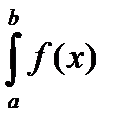dx = – dx .

9) Если f и g интегрируемы на [a , b] и f £ g на [a , b] , то

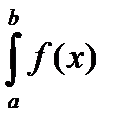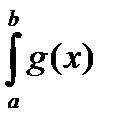dx £ dx .

Для стандартной последовательности интегральных сумм s^m(f)£ s^m(g).