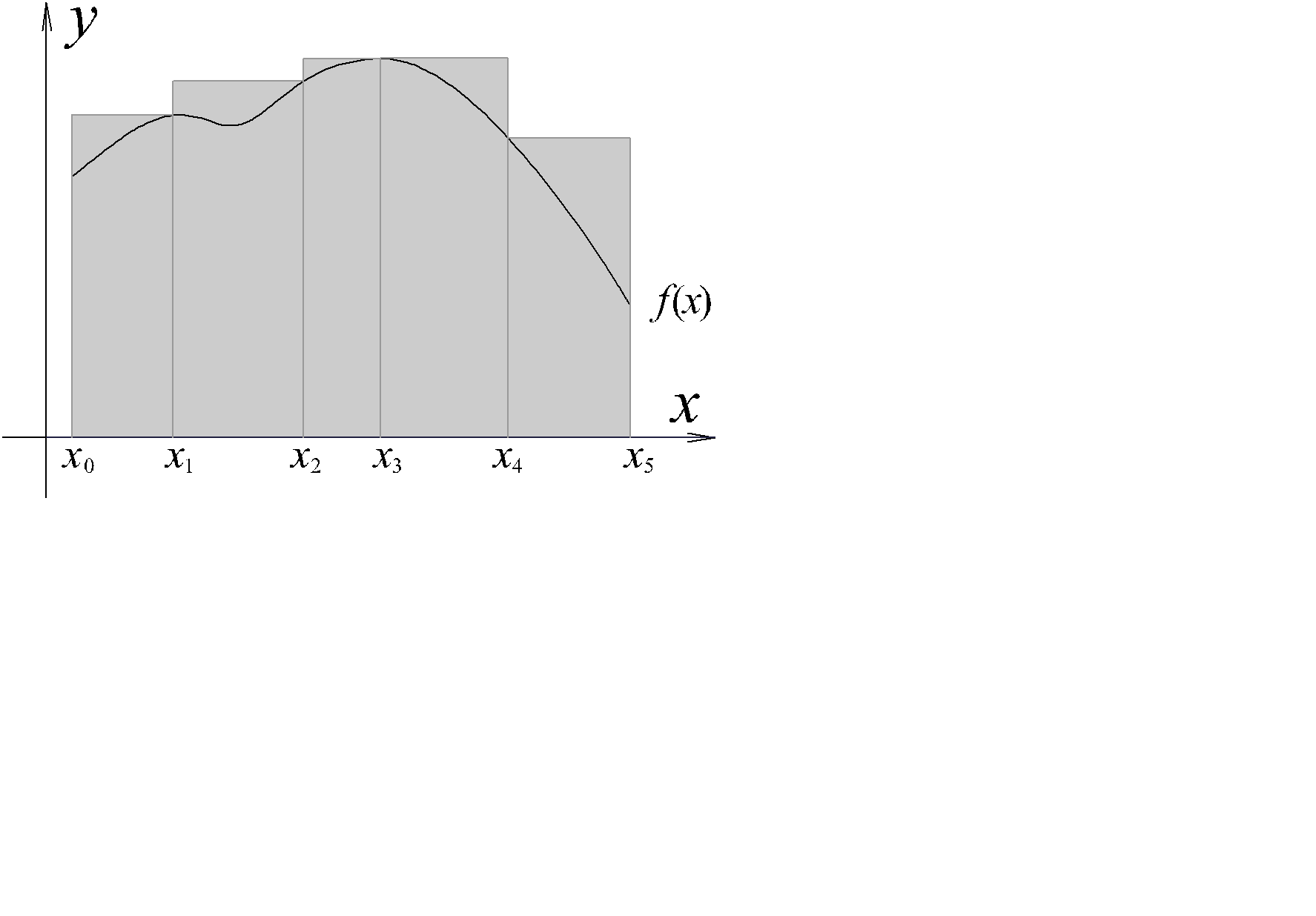
Интегральная сумма (рис. 2.1) представляет собой сумму площадей прямоугольников, построенных на отрезках разбиения [xk , xk+1] с высотой f(xk). При достаточно мелком разбиении D эту суммарную площадь естественно считать приближенно равной площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми x = a , x = b ( здесь мы считаем, что f(x)>0). Такое наблюдение приводит к мысли использовать определенный интеграл для формального определения площадей подобных областей. Общее определение площадей плоских фигур будет рассматриваться в этом курсе позже.
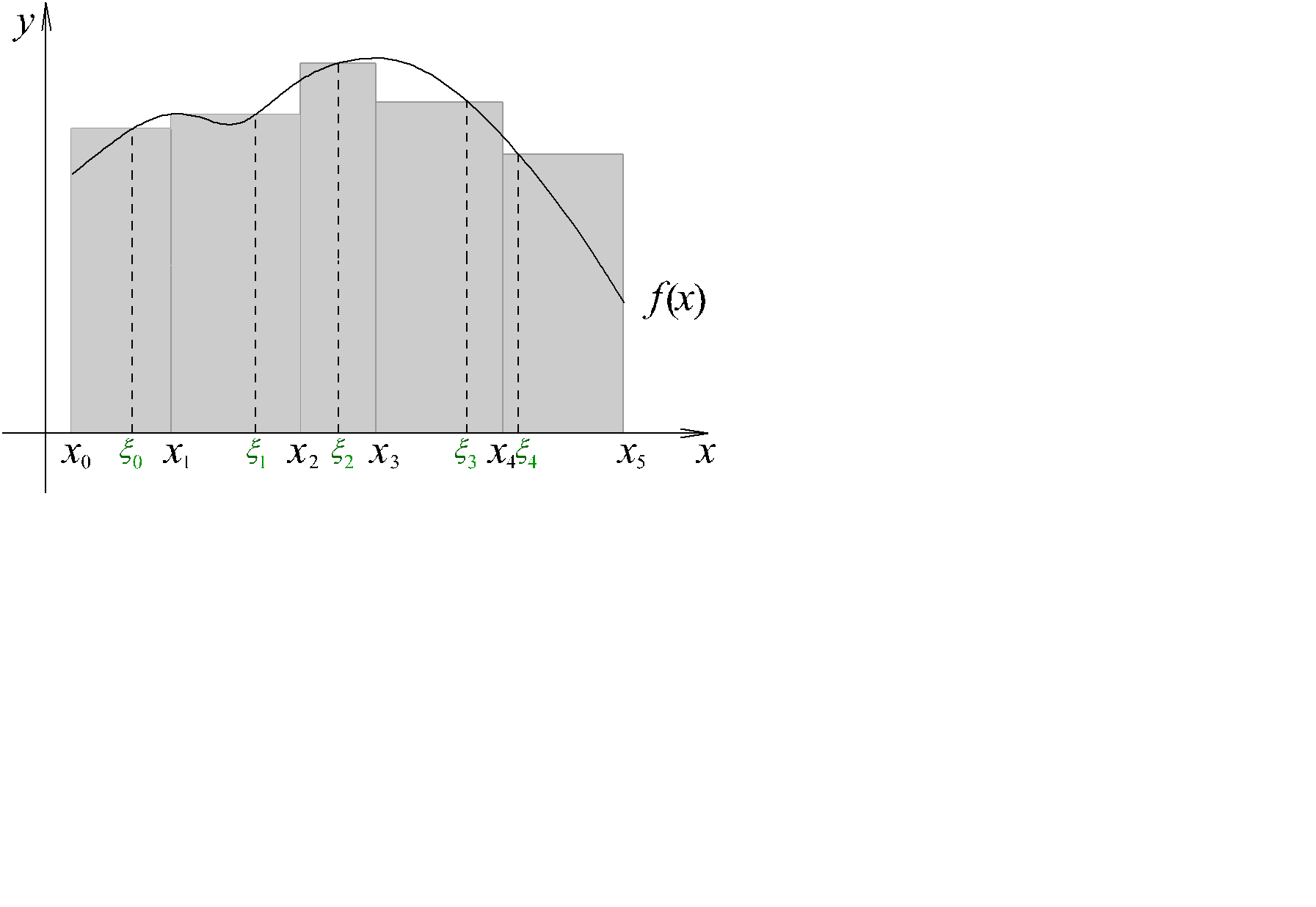
Рис. 2.1
2.1.3. Суммы Дарбу
Пусть функция f(x) определена на [a , b] и D={a = x0< x1<…< xn =b} разбиение отрезка [a , b]. Нижней суммой Дарбу называется сумма s(f,D)= 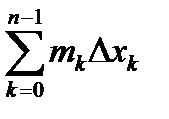 , mk =
, mk = 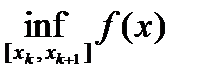 .
.
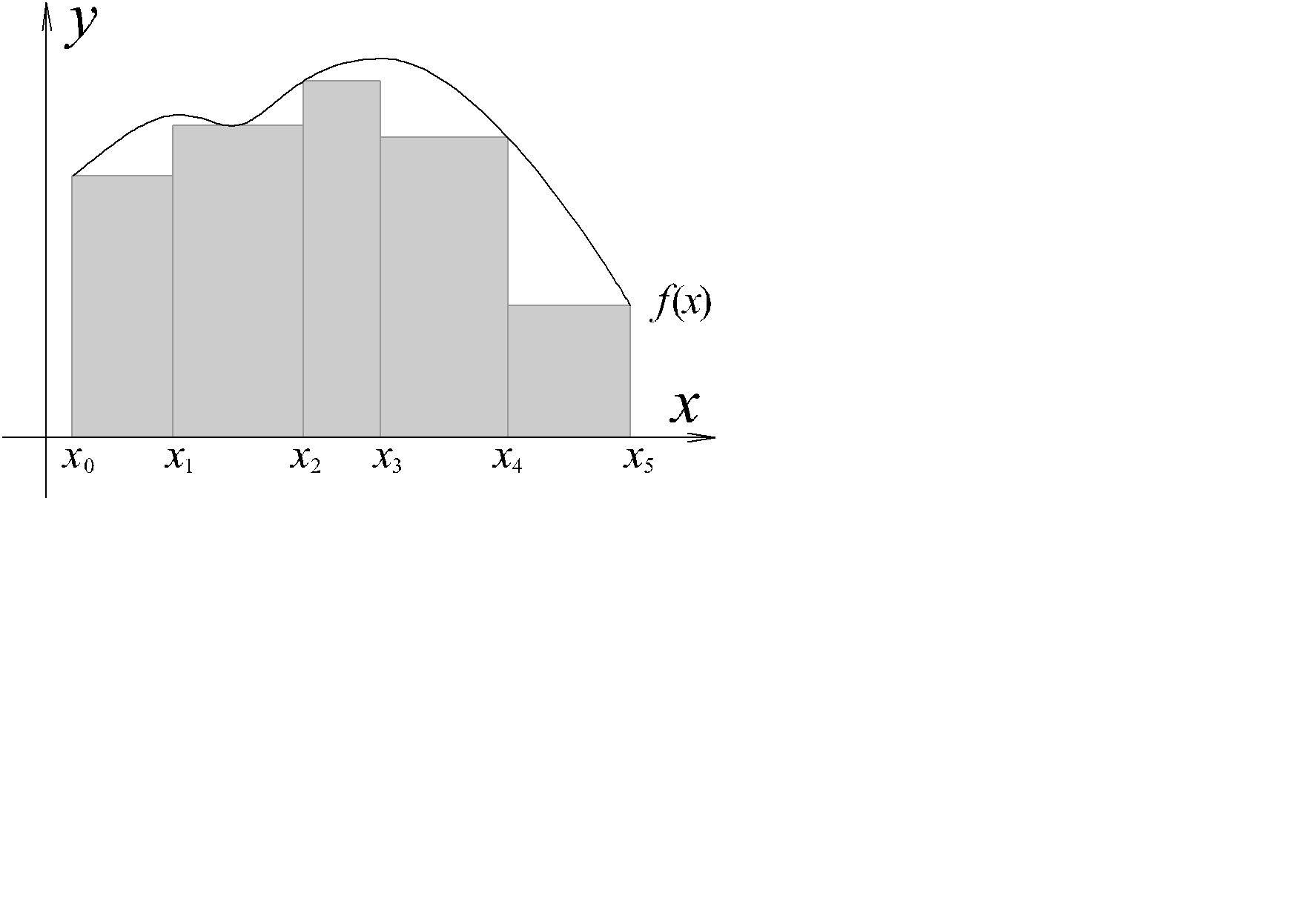
Верхней суммой Дарбу называется сумма S(f ,D)=  , Mk =
, Mk =  .(рис. 2.2, слайд «Суммы Дарбу, интеграл»)
.(рис. 2.2, слайд «Суммы Дарбу, интеграл»)
| 
|
| Геометрический смысл нижних сумм Дарбу. | Геометрический смысл верхних сумм Дарбу. |
Рис. 2.2
Суммы Дарбу, интеграл
Свойства сумм Дарбу
Определение. Если разбиение D2 получено из разбиения D1 добавлением некоторого числа узлов, то говорят, что разбиение D2 следует за разбиением D1 (или D2 является более мелким, чем D1), при этом пишут D1 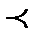 D2 .(см. слайд «Интегральные суммы»)
D2 .(см. слайд «Интегральные суммы»)
Интегральные суммы
1) Для любого разбиения D и набора промежуточных точек xÎD имеют место соотношения
s(f,D) £ s( f,D,x) £ S(f,D), s(f,D) = 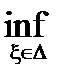 s( f,D,x), S(f,D) =
s( f,D,x), S(f,D) =  s( f,D,x).
s( f,D,x).
Это свойства следует непосредственно из определения интегральных сумм и сумм Дарбу.
2) Если D1 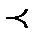 D2 два разбиения данного отрезка, то
D2 два разбиения данного отрезка, то
s(f ,D1) £ s(f ,D2) , S(f ,D2) £ S(f ,D1) .
Другими словами, при измельчении разбиения нижние суммы могут только увеличиться, а верхние суммы могут только уменьшиться.
Это утверждение достаточно доказать для случая, когда второе разбиение получено из первого добавление всего одной точки. Пусть новая точка появилась на отрезке [x¢k , x¢k+1]. Таким образом, во втором разбиении эта точка будет иметь номер k +1 и отрезоку [x¢k , x¢k+1] в первом разбиении будет соответствовать пара отнезков [x¢¢k , x¢¢k+1] , [x¢¢k+1, x¢¢k+2] во втором разбиении и [x¢k , x¢k+1] =[x¢¢k , x¢¢k+1] È[x¢¢k+1, x¢¢k+2]. См. рисунок 2.3 и слайд «Измельчение разбиения».
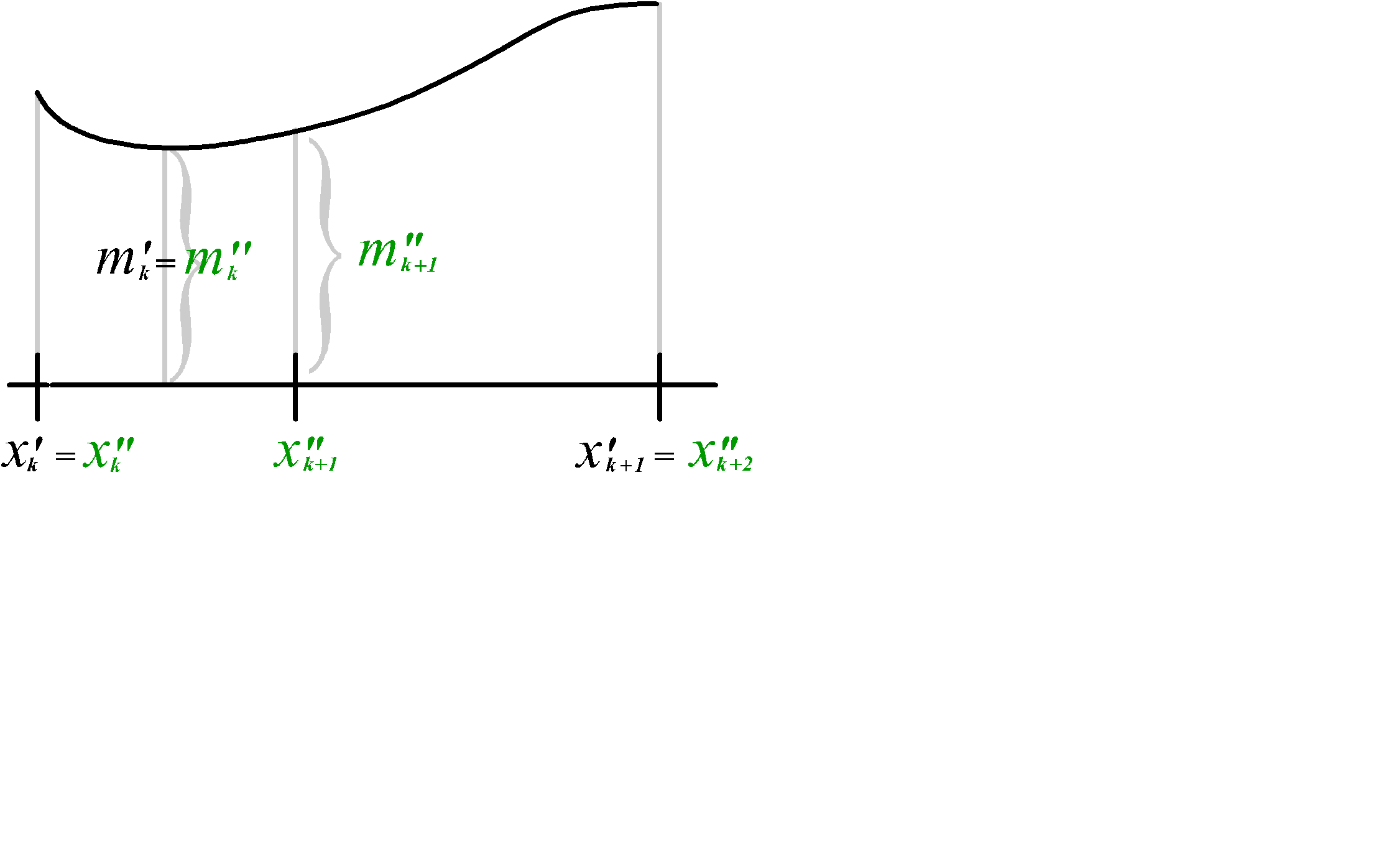
Рис. 2.3
Измельчение разбиения
Рассмотрим нижние суммы Дарбу. Нижняя грань функции по всему множеству [x¢k , x¢k+1] будет меньше или равна, чем нижняя грань по части этого множества, поэтому выполнены неравнства m¢k £ m¢¢k , m¢k £ m¢¢k+1. Отличие сумм s(f ,D1), s(f ,D2) состоит в том, что во второй сумме вместо слагаемого m¢k(x¢k +1 - x¢k) появились два слагаемых m¢¢k D¢¢k + m¢¢k+1 D¢¢k+1. Остальные слагаемые в обеих суммах будут одинаковыми.
Таким образом,
s(f ,D1) = A + m¢k D¢k +B,
s(f ,D2) = A+ m¢¢k D¢¢k + m ¢¢ k +1 D¢¢k+1 +B, следовательно
s(f,D2) - s(f,D1) = m¢¢k D¢¢k + m ¢¢ k+1 D¢¢k+1 - m¢k D¢k = m¢¢k D¢¢k + m¢¢k+1 D¢¢k+1 -
- m¢k (D¢¢k +D¢¢k+1) = (m¢¢k - m¢k) D¢¢k +( m¢¢k+1 - m¢k ) D¢¢k+1 ³ 0.
Здесь D¢k = x¢k+1 - x¢k = x¢¢k+2 - x¢¢k = x¢¢k+2 - x¢¢k+1 + x¢¢k+1 - x¢¢k = D¢¢k+1 +D¢¢k .
Аналогично доказывается утверждение для верхних сумм Дарбу.
3) Для любых разбиений D1 ,D2 данного отрезка справедливо неравенство
s(f ,D1) £ S(f ,D2).
Обозначим через D3 = D1 ÈD2 разбиение, образованное всеми узлами двух исходных разбиений. Очевидно D1  D3 , D2
D3 , D2  D3 . Тогда, как это следует из предыдущего свойства
D3 . Тогда, как это следует из предыдущего свойства
s(f ,D1) £ s(f ,D3) £ S(f ,D3) £ S(f ,D2),
откуда и следует доказываемое неравенство (см. слайд «Объединение разбиений»).
Объединение разбиений
2.1.5. Нижний и верхний интегралы
Определение. Колебанием функции f(x) на отрезке [xk,xk+1] будем называть величину
wk (f) = sup |f(x) – f(y)| = Mk – mk , где точная верхняя грань берется по всевозможным x, y из отрезка [xk,xk+1], mk = 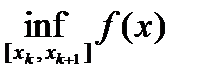 , Mk =
, Mk =  .
.
Отметим, что для разбиения D будет выполнено равенство (см. слайд «Нижние и верхние суммы Дарбу»)
S(f,D) - s(f,D) =  .
.
Нижние и верхние суммы Дарбу
Определение. Нижним интегралом  называется точная верхняя грань значений нижних сумм Дарбу
называется точная верхняя грань значений нижних сумм Дарбу 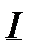 = sup s(f ,D), где верхняя грань берется по всевозможным разбиениям отрезка [a , b]. Аналогично определяется верхний интеграл
= sup s(f ,D), где верхняя грань берется по всевозможным разбиениям отрезка [a , b]. Аналогично определяется верхний интеграл 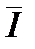 , как точная нижняя грань значений верхних сумм Дарбу
, как точная нижняя грань значений верхних сумм Дарбу 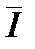 = inf S(f ,D), где точная грань берется по всевозможным разбиениям отрезка [a , b].
= inf S(f ,D), где точная грань берется по всевозможным разбиениям отрезка [a , b].
Для ограниченной функции существует, как нижний, так и верхний интегралы. Это следует из того, что множество значений нижних сумм Дарбу ограничено сверху, например, значением любой верхней суммы Дарбу. Множества верхних сумм Дарбу ограничено снизу, например, значением любой нижней суммой Дарбу.
Теорема. Для любого разбиения D данного отрезка справедливы неравенства
s(f ,D) £  £
£ 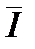 £ S(f ,D).
£ S(f ,D).
Доказательство. Не очевидным является только неравенство  £
£ 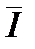 . Предположим противное, т.е., что
. Предположим противное, т.е., что 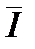 <
<  .
.
Выберем непересекающиеся e окрестности точек 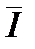 ,
,  , тогда
, тогда 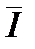 +e <
+e <  - e. По определениям точных граней найдутся два разбиения D1 , D2 такие, что S(f ,D1)<
- e. По определениям точных граней найдутся два разбиения D1 , D2 такие, что S(f ,D1)< 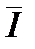 +e <
+e <  - e < s(f ,D2), что противоречит свойству 3) сумм Дарбу (Рис. 2.4, см. слайд «К доказательству теоремы»).
- e < s(f ,D2), что противоречит свойству 3) сумм Дарбу (Рис. 2.4, см. слайд «К доказательству теоремы»).
Рис. 2.4
К доказательству теоремы
2.1.6. Критерий интегрируемости. Теорема Дарбу
Теорема Дарбу. Для того, чтобы ограниченная функция была интегрируемой на отрезке [a,b], необходимо и достаточно, чтобы разность сумм Дарбу (см. слайд «Критерий интегрируемости»)
S(f ,D) - s(f ,D) ® 0 при l(D)®0. (2.1)
Критерий интегрируемости
То есть существование интеграла 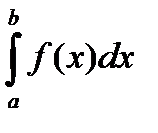 эквивалентно выполнению условие
эквивалентно выполнению условие
"e>0$d>0"D,l(D)<d: S ( f,D) - s(f,D)<e.
Доказательство. Необходимость. Пусть f(x) интегрируема и J = 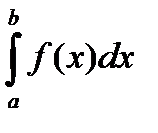 . Возьмем какое-либо e>0 для него $d>0 такое, что при l(D)<d будет выполнено неравенство
. Возьмем какое-либо e>0 для него $d>0 такое, что при l(D)<d будет выполнено неравенство
|s( f ,D,x)–J |<e/3 ( для любых xÎD ).
так как s(f ,D) = 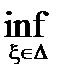 s( f ,D,x), S(f ,D) =
s( f ,D,x), S(f ,D) = 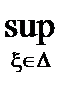 s( f ,D,x), то
s( f ,D,x), то
| S(f ,D) - J |≤ e /3, | J - s(f ,D)| ≤ e/3
тогда
|S(f,D) - s(f,D)|=|S(f,D) - J + J - s(f,D)| £ |S(f,D) - J| +| J - s(f,D)| £ 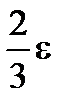 <e .
<e .
Достаточность. Разность сумм Дарбу может быть сделана сколь угодно малой выбором достаточно мелкого разбиения. Как уже отмечалось (2.1), нижний и верхний интегралы существуют и
s(f ,D) £ 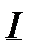 £
£ 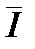 £ S(f ,D),
£ S(f ,D),
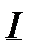 = sup s(f,D),
= sup s(f,D), 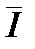 = inf S(f,D).
= inf S(f,D).
Так как 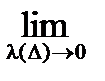 (S(f ,D) - s(f ,D)) = 0 , то
(S(f ,D) - s(f ,D)) = 0 , то 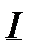 =
= 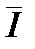 . Положим I =
. Положим I = 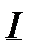 =
= 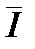 . Из условия (2.1) и неравенств s(f,D) £ s( f,D,x) £ S(f,D) следует, что |s(f ,D,x) – I | £ S(f ,D) - s(f ,D) (рис. 2.5).
. Из условия (2.1) и неравенств s(f,D) £ s( f,D,x) £ S(f,D) следует, что |s(f ,D,x) – I | £ S(f ,D) - s(f ,D) (рис. 2.5).
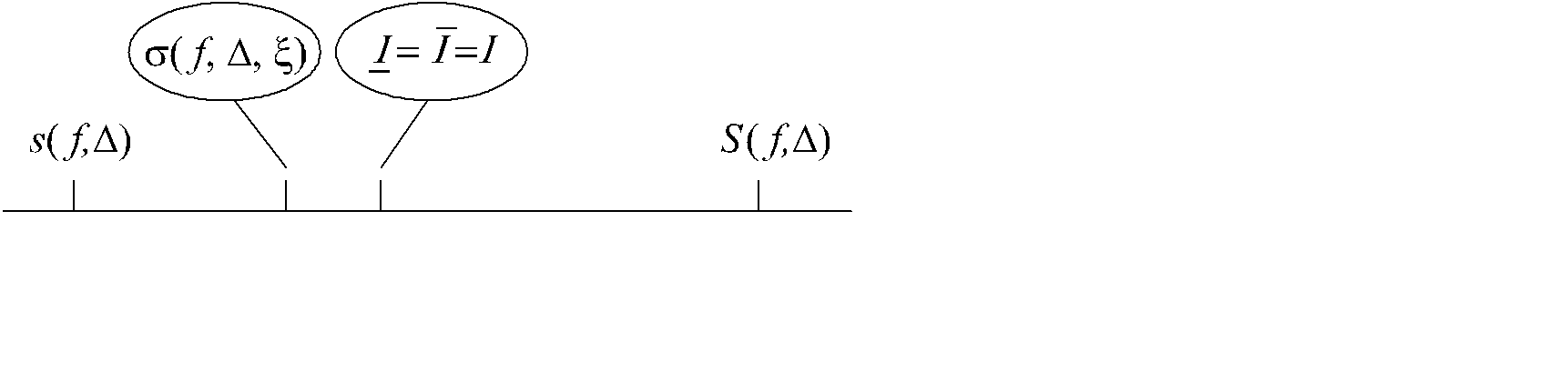
Рис. 2.5
Откуда и получается требуемое утверждение.
2.2. Классы интегрируемых функций, свойства определенного интеграла
Интегрируемость непрерывных функций и некоторых других классов функций. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.
2.2.1. Непрерывные функции
Теорема 1. Всякая непрерывная на отрезки [a , b] функция интегрируема на этом отрезке.
Доказательство. Как ранее отмечалось
S(f ,D) - s(f ,D) = 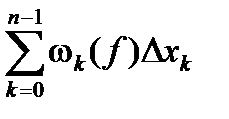 , wk (f) = Mk – mk .
, wk (f) = Mk – mk .
По теореме Кантора для любого e > 0 существует d > 0 такое, что при l(D)<d будет выполнено неравенство wk(f)< 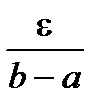 . Тогда
. Тогда
S(f ,D) - s(f ,D) = 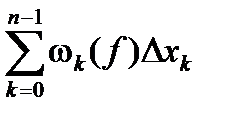 <
< 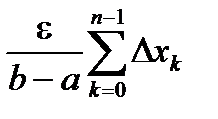 =e .
=e .
Дата: 2019-03-05, просмотров: 418.