a) 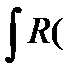sin x , cos x ) dx

Универсальная тригонометрическая подстановка 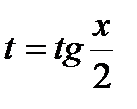, x =2 arctg t ,

sin x = 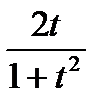, cos x = 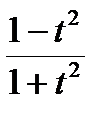. Иногда к цели быстрее ведут подстановки t =sin x , t =cos x ,  .

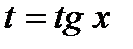б) 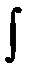sin^mx cosⁿx dx , m и n – рациональные.

Замена  t = sin x ( или t = cos x ), cos x = 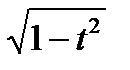, dt = 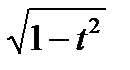dx , тогда

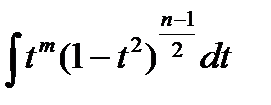sin^mx cosⁿx dx = . Точно также для областей интегрирования, где .

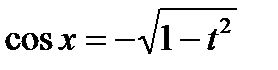в) Интегралы вида 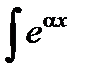cos bx dx, 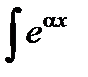sin bx dx,  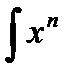arccos bx dx,   ,

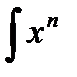 arcsin bx dx,  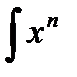arctg bx dx,  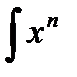arcctg bx dx , 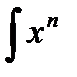ln x dx вычисляются методом интегрирования по частям.

1.3. 5. Интегралы, не выражающиеся через элементарные функции

  а) Дифференциальные биномы

(a + bxⁿ)^p x^m , когда не является целой ни одна из трех дробей 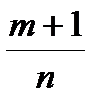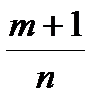p , , + p .

  б) Интеграл .

  в) Интегралы вида 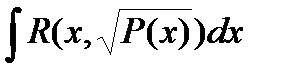, где - многочлен степени 3, 4 в ряде случаев не выражается через элементарные функции (эллиптические интегралы ). В частности, следующие интегралы не являются элементарными функциями

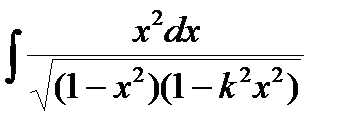, , 0< k <1;

или ( после замены )

, .

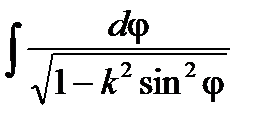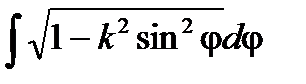Часть 2. Определенный интеграл

2.1. Интеграл Римана

Определение интеграла Римана. Критерий интегрируемости.

Определения

Пусть функция f(x) определена на [a , b]. Разбиением отрезка [a , b] называется набор точек  D={a = x₀< x₁<…< x_n =b}. Обозначим через x набор промежуточных точек для D, x={x_k}, x_k Î[x_k , x_{k +1}], k =0,1,…, n -1. Интегральной суммой для f , D и x называется выражение

Величина l(D)= 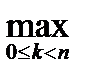(x_{k +1} - x_k) называется характеристикой разбиения D, точки x_k называются узлами разбиения. Если промежуточные точки x={x_k} выбраны для данного разбиения D (т.е. x_kÎ[x_k , x_k+1]), то мы будем это обозначать знаком принадлежности xÎD.

Определение. Предел интегральных сумм s(f ,D,x) при l(D)®0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется определенным интегралом от функции f на отрезке[a , b] и обозначается

= .

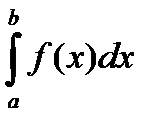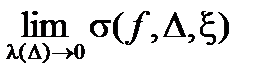Более точно это определение выглядит следующим образом:

$J"e>0$d>0:(l(D)<d,xÎD) Þ |s(f ,D,x) - J |<e или

$J"e>0$d>0"D, l(D)<d,"xÎD : |s(f ,D,x) - J |<e.

Функция f(x), для которой существует интеграл 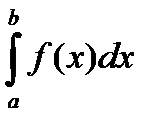, называется интегрируемой (по Риману) на данном отрезке.

Пусть функция f(x) интегрируема на [a , b]. Выберем последовательность разбиений 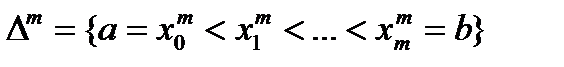 , с равноотстоящими узлами  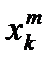= a + 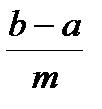k , k =0,1,…, m. Тогда 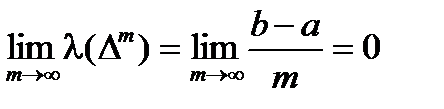. Для каждого из этих разбиений будем считать заданным некоторый набор промежуточных точек 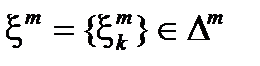, например, можно выбирать средние точки 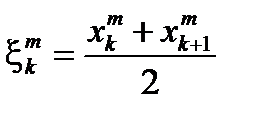.   Полученную таким образом последовательность интегральных сумм 

s^m = s( f ,D^m ,x^m)= 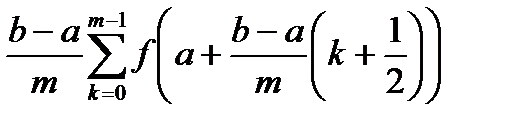 будем называть стандартной последовательностью интегральных сумм.

Из определения интеграла следует, что

=

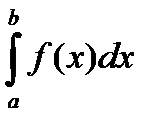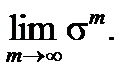
 Таким образом, если функция 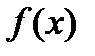интегрируема и s^m ее стандартная последовательность интегральных сумм, то

= = .

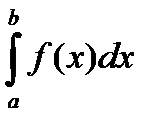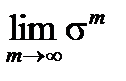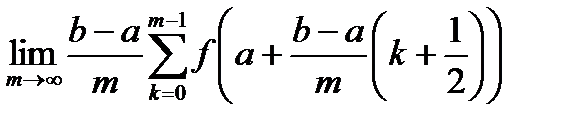В качестве последовательности, реализующей значение интеграла можно брать суммы, где промежуточные точки совпадают с левыми или правыми концами отрезков разбиения. Например, для левых концов

= .

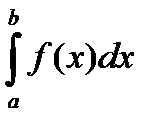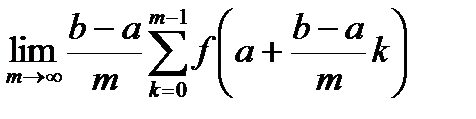Формулы вычисления интегралов подобного вида называются квадратурными формулами.

Пример 1. Частный случай. Если функция f интегрируема на [0,1], то

= .

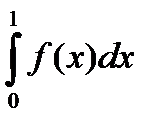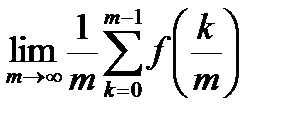Пример 2. Вычислить предел .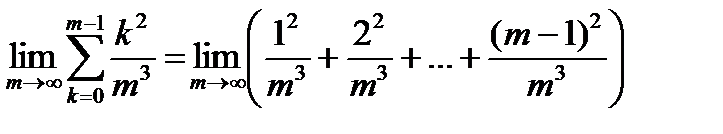

Суммы  является интегральными для функции 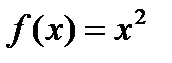 на отрезке  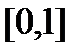при выборе промежуточных точек, как в предыдущем примере, поэтому

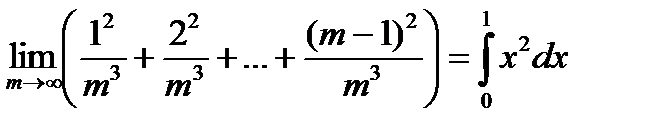. В дальнейшем появятся формулы для вычисления интегралов. В нашем случае будет .

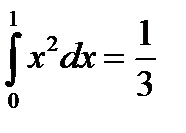Теорема. Если функция интегрируема, то она ограничена.

Доказательство. Предположим противное, функция f(x) не ограничена на отрезке [a , b]. Тогда найдется последовательность t ^m Î[a , b], сходящаяся 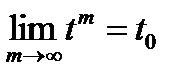 и такая, что 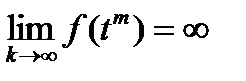. Пусть e=1 для него

$d>0:(l(D)<d,xÎD) Þ |s(f ,D,x) - J |<1,

где 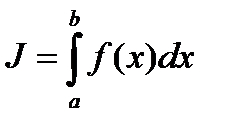. Таким образом, если разбиение D имеет характеристику l(D)<d  , то интегральная сумма s(f ,D,x) ограничена  |s(f,D,x)| , не зависимо от выбора промежуточных точек . С другой стороны любую интегральную сумму s(f ,D,x) можно сделать сколь угодно большой, выбрав подходящим образом лишь одну из промежуточных точек, полагая ее равной соответствующему члену последовательности . Полученное противоречие завершает доказательство.