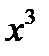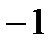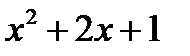1.1. Первообразная, неопределенный интеграл
Первообразная и неопределенный интеграл. Свойства неопределенных интегралов. Основные методы интегрирования. Замена переменного и интегрирование по частям.
Определения
Интегрирование – обратная операция к дифференцированию.
Пусть X – связное множество, т.е. множество, которое вместе с любыми двумя своими точками содержит и отрезок, их соединяющий. Функция F(x) называется первообразной для функции f(x) на связном множестве X , если F ¢(x) = f(x).
Примеры:
1) f(x)=0, F(x)=C (Const), X=(-¥,¥),
2) f(x)=a (Const), F(x)=a x+C, X=(-¥,¥),
3) f(x)=cos x, F(x)= 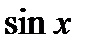 +C, X=(-¥,¥),
+C, X=(-¥,¥),
4) f(x)=1/x, F(x)=ln x+C, X=(0,¥),
5) f(x)=1/x, F(x)=ln |x|+C, X=(-¥ , 0).
Замечание. Если F – первообразная для f на связном множестве X , то G = F + C также является первообразной для f , и наоборот, если G , F - первообразные для f , то G = F + C (Следствие из теоремы Лагранжа).
Пример. Функции F = ln | x | и G =ln| x | + sign x имеют общую производную, равную f(x)=1/x на множестве X =(-¥,0)È(0,¥), в то время, как их разность 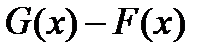 =sign x и, таким образом, не являются константой на X. Из этого примера слелует, что условие: « X – связное» – существенно. Говоря о первообразной на каком-то множестве, всегда будет предполагаться, что это множество связное.
=sign x и, таким образом, не являются константой на X. Из этого примера слелует, что условие: « X – связное» – существенно. Говоря о первообразной на каком-то множестве, всегда будет предполагаться, что это множество связное.
Определение. Совокупность всех первообразных для функции f на связном множестве X (если они существуют), называется неопределенным интегралом функции f и обозначается
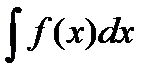
См. слайд «Неопределенный интеграл».
Неопределенный интеграл
Таким образом, если F – первообразная для f на X, то
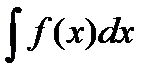 =F ( x )+ C на множестве X .
=F ( x )+ C на множестве X .
Замечание. В обозначении неопределенного интеграла 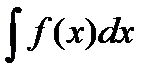 буква x несет смысловую нагрузку переменной для функции F(x)+ C . Так, если x =j(t), то можно написать
буква x несет смысловую нагрузку переменной для функции F(x)+ C . Так, если x =j(t), то можно написать
F(j(t))+ C = 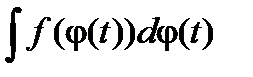 .
.
Другими словами, интеграл справа понимается, как суперпозиция функций 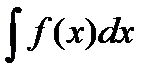 и x =j(t).
и x =j(t).
Свойства неопределенного интеграла
1) 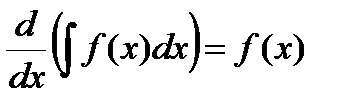 , в частности,
, в частности, 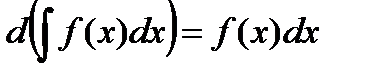 .
.
2) 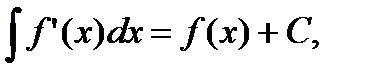
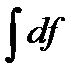 = f + C .
= f + C .
3) 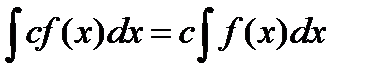 , с точностью до аддитивной постоянной.
, с точностью до аддитивной постоянной.
4) 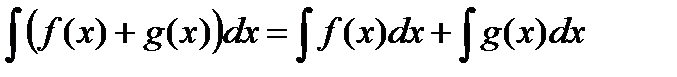 , с точностью до аддитивной постоянной.
, с точностью до аддитивной постоянной.
Все эти свойства проверяются непосредственно по определению. Например, второе свойство. Производная функции 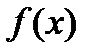 равна
равна 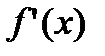 , поэтому
, поэтому 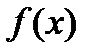 является первообразной для функции
является первообразной для функции 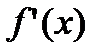 . Любая другая первообразная отличается от нее на константу. Таким образом,
. Любая другая первообразная отличается от нее на константу. Таким образом, 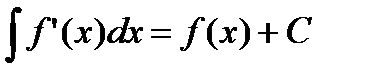 . В четвертом свойстве необходимо добавить следующее замечание. Равенство
. В четвертом свойстве необходимо добавить следующее замечание. Равенство 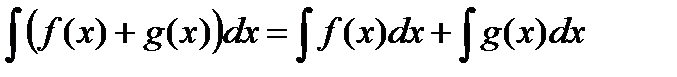 следует понимать так. Для любой первообразной
следует понимать так. Для любой первообразной 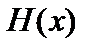 из множества функций
из множества функций 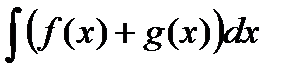 найдутся первообразные
найдутся первообразные 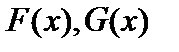 из множеств
из множеств 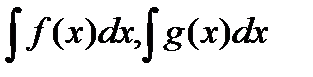 , такие, что
, такие, что 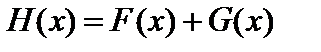 . И наоборот, для любой пары функций
. И наоборот, для любой пары функций 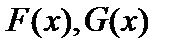 из множеств
из множеств 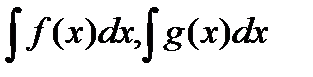 , их сумма
, их сумма 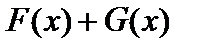 будет принадлежать множеству
будет принадлежать множеству 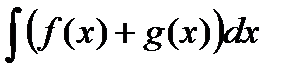 .
.
Таблица неопределенных интегралов
Из таблицы производных можно получить таблицу интегралов.
1) 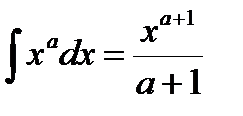 + С, a ¹ - 1.
+ С, a ¹ - 1.
2) 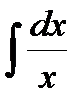 = ln| x | + С, X ={x>0} или X ={ x<0 }, но не на X =(-¥,0)È(0,¥) .
= ln| x | + С, X ={x>0} или X ={ x<0 }, но не на X =(-¥,0)È(0,¥) .
3) 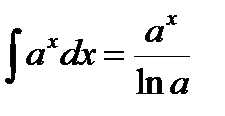 + C, a¹1,
+ C, a¹1, 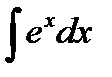 =ex+C.
=ex+C.
4) 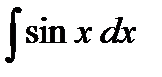 = - cos x + C,
= - cos x + C, 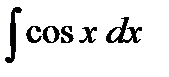 = sin x + C.
= sin x + C.
5) 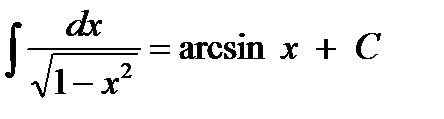 ,
, 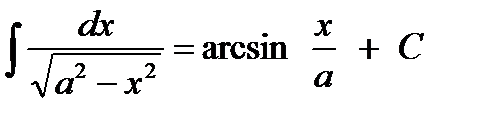 ,
, 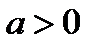 .
.
6) 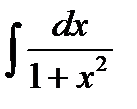 = arctg x + C,
= arctg x + C, 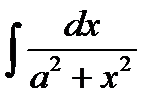 =
= 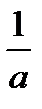 arctg
arctg 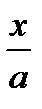 + C.
+ C.
7) 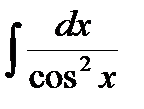 =tg x + C,
=tg x + C, 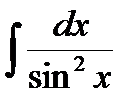 =- ctg x + C.
=- ctg x + C.
8) 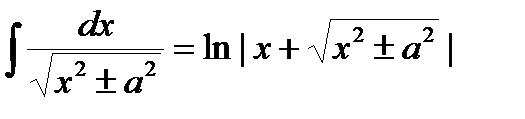 + C.
+ C.
9) 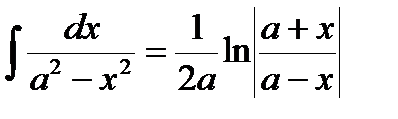 + C.
+ C.
10) 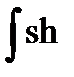 x dx = ch x + C,
x dx = ch x + C, 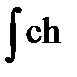 x dx = sh x + C.
x dx = sh x + C.
11) 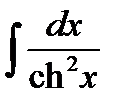 = th x + C ,
= th x + C , 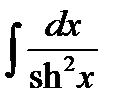 = -cth x + C .
= -cth x + C .
1.1.4. Замена переменного
Если F(x)– первообразная для f(x) на X т.е. 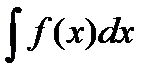 =F(x)+ C , функция x =j(t) дифференцируема на T и определена суперпозиция
=F(x)+ C , функция x =j(t) дифференцируема на T и определена суперпозиция 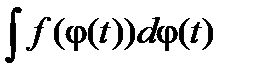 = F(j(t))+ C , тогда функция F(t)= f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,
= F(j(t))+ C , тогда функция F(t)= f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,
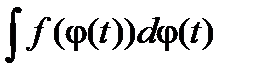 =
= 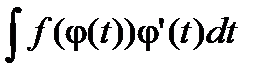 (формула замены переменного).
(формула замены переменного).
Для доказательства достаточно продифференцировать левую и правую части и убедиться, что получится одна и та же функция.
Примеры:
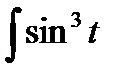 cos t dt =
cos t dt = 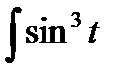 d sin t =
d sin t = 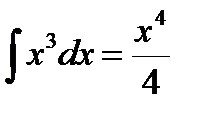 + C =
+ C = 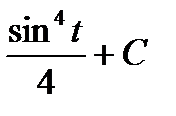 .
.
J = 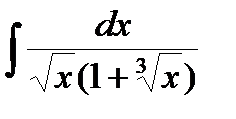 , сделаем замену x = t6, тогда
, сделаем замену x = t6, тогда
J=6 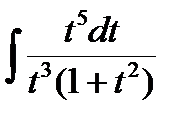 =6
=6 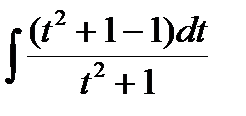 =6t – 6 arctg t + C =6
=6t – 6 arctg t + C =6 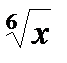 –6 arctg
–6 arctg 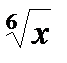 +C.
+C.
Интегрирование по частям
Если u(x), v(x) – дифференцируемы на отрезке X и существует
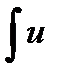 dv =
dv = 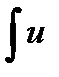 (x)v ¢(x)dx , тогда существует и интеграл
(x)v ¢(x)dx , тогда существует и интеграл 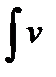 du и выполняется равенство
du и выполняется равенство
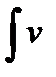 du = uv -
du = uv - 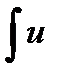 dv (формула интегрирования по частям).
dv (формула интегрирования по частям).
Доказательство. Пусть 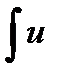 dv = F(x)+ C. Тогда функция uv – F будет первообразной для
dv = F(x)+ C. Тогда функция uv – F будет первообразной для 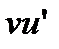 , что можно проверить дифференцированием:
, что можно проверить дифференцированием: 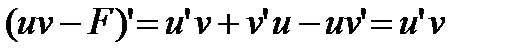 . Можно было продифференцировать левую и правую части и убедится, что получится одна и та же функция.
. Можно было продифференцировать левую и правую части и убедится, что получится одна и та же функция.
Пример. Для интеграла 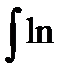 x dx выберем функции: v(x) = ln x , u(x) = x , тогда
x dx выберем функции: v(x) = ln x , u(x) = x , тогда
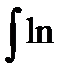 x dx =x ln x -
x dx =x ln x - 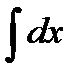 =x ln x – x + C.
=x ln x – x + C.
1.2. Разложение рациональной функции на простейшие дроби и их интегрирование
Разложение дроби на элементарные. Метод неопределенных коэффициентов.
Предварительные сведения из алгебры многочленов
а) Если a вещественный корень многочлена 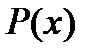 , то существует единственное представление многочлена в виде
, то существует единственное представление многочлена в виде
P(x ) = 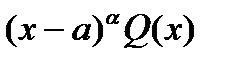 , a ³ 1, и
, a ³ 1, и 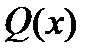 - многочлен, причем
- многочлен, причем 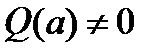 .
.
Число a называется кратностью корня. Другое эквивалентное определение кратности корня дается в терминах производных: a – это порядок первой, не равной нулю производной в точке a : P(a)= P ¢(a)=…= P(a-1)(a)=0, P(a)(a)¹0.
Доказательство этого свойства следует из формулы Тейлора для многочлена 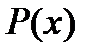 . Действительно, пусть
. Действительно, пусть 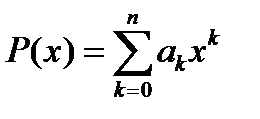 . Очевидно, что все производные этого многочлена, начиная с порядка
. Очевидно, что все производные этого многочлена, начиная с порядка 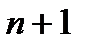 , будут тождественно равны нулю. Поэтому разложение функции
, будут тождественно равны нулю. Поэтому разложение функции 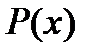 по формуле Тейлора в точке
по формуле Тейлора в точке 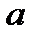 будет иметь вид (остаток в форме Лагранжа тождественно равен нулю)
будет иметь вид (остаток в форме Лагранжа тождественно равен нулю)
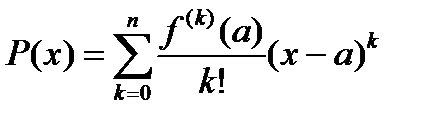 .
.
Если число 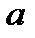 является корнем многочлена
является корнем многочлена 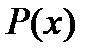 и
и 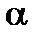 - порядок первой отличной от нуля производной
- порядок первой отличной от нуля производной 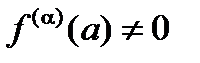 , то
, то
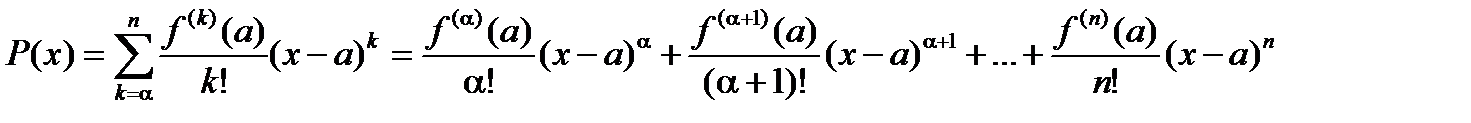 =
= 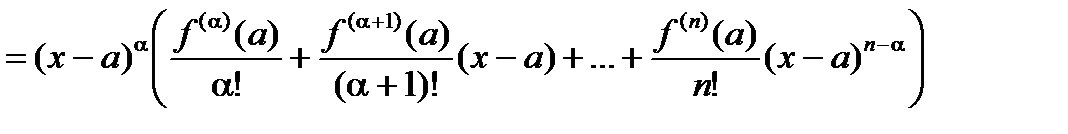 =
= 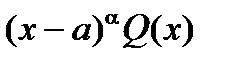 ,
, 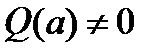 .
.
б) Если z = u + i v , v¹0 комплексный корень многочлена с действительными коэффициентами, то сопряженное комплексное число 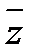 = u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения:
= u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения: 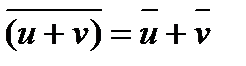 ,
, 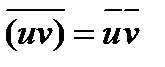 , для действительного числа x справедливо равенство
, для действительного числа x справедливо равенство 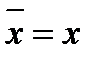 . Поэтому, если z корень многочлена P(x) = a0+…+ akxk +…+ anxn , то
. Поэтому, если z корень многочлена P(x) = a0+…+ akxk +…+ anxn , то 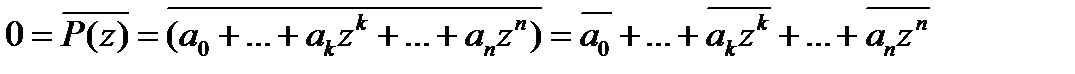 =
= 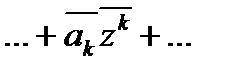 = =
= = 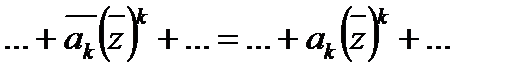 =P(
=P( 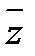 ).
).
Тогда существует единственное представление многочлена в виде
P(x) = (x2+px+q)b 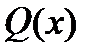 , b ³ 1, Q(z)¹0,
, b ³ 1, Q(z)¹0,
(x - z)(x - 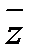 )=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
)=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
в) Любой многочлен можно разложить в произведение по своим корням
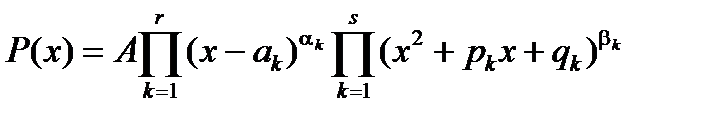 ,
,
где A – старший коэффициент многочлена, a1, a2,…, ar -действительные корни кратностей a1, a2,…, a r , а z1, z2,…, zs комплексные корни кратностей b1,b2,…, bs . Связь между комплексными корнями и сомножителями в разложении многочлена следующая x 2 + pkx + qk =(x - zk)(x - 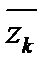 ).
).
Определение . Рациональная функция ( отношение двух многочленов) 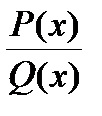 ) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
Утверждение. Любую рациональную функцию можно представить в виде многочлена (целая часть) плюс правильная дробь .
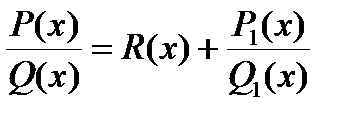 , - R ( x ) – многочлен, дробь
, - R ( x ) – многочлен, дробь 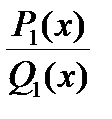 - правильная.
- правильная.
R(x) –называется целой частью, а дробь P1/Q1 –остатком. Остаток и целую часть можно получить делением «уголком».
Пример: Выделить целую и дробную часть 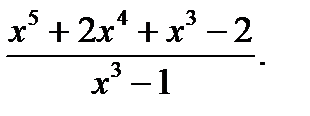
| 
| 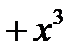
| 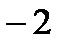
| | ||||
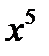
| 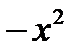
| | ||||||
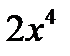
| 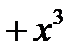
| 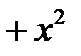
| 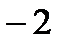
|
| ||||
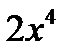
| 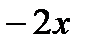
|
| ||||||
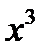
| 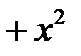
| 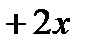
| 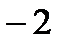
|
| ||||
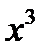
| 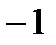
|
| ||||||
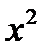
| 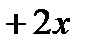
| 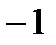
|
| |||||
Таким образом, 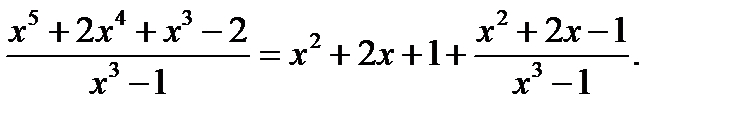
Дата: 2019-03-05, просмотров: 372.