Интегральное исчисление и функции многих переменных
Часть 1. Интегральное исчисление
1.1. Первообразная, неопределенный интеграл
Первообразная и неопределенный интеграл. Свойства неопределенных интегралов. Основные методы интегрирования. Замена переменного и интегрирование по частям.
Определения
Интегрирование – обратная операция к дифференцированию.
Пусть X – связное множество, т.е. множество, которое вместе с любыми двумя своими точками содержит и отрезок, их соединяющий. Функция F(x) называется первообразной для функции f(x) на связном множестве X , если F ¢(x) = f(x).
Примеры:
1) f(x)=0, F(x)=C (Const), X=(-¥,¥),
2) f(x)=a (Const), F(x)=a x+C, X=(-¥,¥),
3) f(x)=cos x, F(x)= 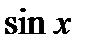 +C, X=(-¥,¥),
+C, X=(-¥,¥),
4) f(x)=1/x, F(x)=ln x+C, X=(0,¥),
5) f(x)=1/x, F(x)=ln |x|+C, X=(-¥ , 0).
Замечание. Если F – первообразная для f на связном множестве X , то G = F + C также является первообразной для f , и наоборот, если G , F - первообразные для f , то G = F + C (Следствие из теоремы Лагранжа).
Пример. Функции F = ln | x | и G =ln| x | + sign x имеют общую производную, равную f(x)=1/x на множестве X =(-¥,0)È(0,¥), в то время, как их разность 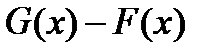 =sign x и, таким образом, не являются константой на X. Из этого примера слелует, что условие: « X – связное» – существенно. Говоря о первообразной на каком-то множестве, всегда будет предполагаться, что это множество связное.
=sign x и, таким образом, не являются константой на X. Из этого примера слелует, что условие: « X – связное» – существенно. Говоря о первообразной на каком-то множестве, всегда будет предполагаться, что это множество связное.
Определение. Совокупность всех первообразных для функции f на связном множестве X (если они существуют), называется неопределенным интегралом функции f и обозначается
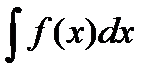
См. слайд «Неопределенный интеграл».
Неопределенный интеграл
Таким образом, если F – первообразная для f на X, то
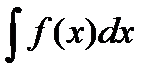 =F ( x )+ C на множестве X .
=F ( x )+ C на множестве X .
Замечание. В обозначении неопределенного интеграла 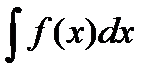 буква x несет смысловую нагрузку переменной для функции F(x)+ C . Так, если x =j(t), то можно написать
буква x несет смысловую нагрузку переменной для функции F(x)+ C . Так, если x =j(t), то можно написать
F(j(t))+ C = 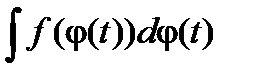 .
.
Другими словами, интеграл справа понимается, как суперпозиция функций 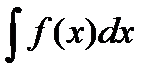 и x =j(t).
и x =j(t).
Свойства неопределенного интеграла
1) 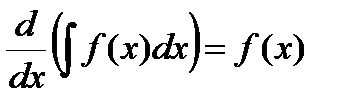 , в частности,
, в частности,  .
.
2) 
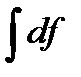 = f + C .
= f + C .
3) 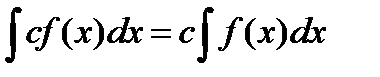 , с точностью до аддитивной постоянной.
, с точностью до аддитивной постоянной.
4)  , с точностью до аддитивной постоянной.
, с точностью до аддитивной постоянной.
Все эти свойства проверяются непосредственно по определению. Например, второе свойство. Производная функции 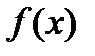 равна
равна 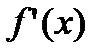 , поэтому
, поэтому 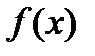 является первообразной для функции
является первообразной для функции 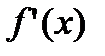 . Любая другая первообразная отличается от нее на константу. Таким образом,
. Любая другая первообразная отличается от нее на константу. Таким образом, 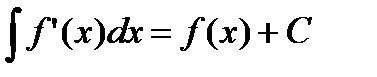 . В четвертом свойстве необходимо добавить следующее замечание. Равенство
. В четвертом свойстве необходимо добавить следующее замечание. Равенство  следует понимать так. Для любой первообразной
следует понимать так. Для любой первообразной  из множества функций
из множества функций 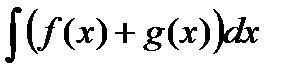 найдутся первообразные
найдутся первообразные 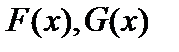 из множеств
из множеств 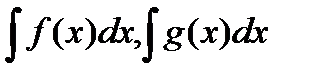 , такие, что
, такие, что 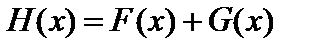 . И наоборот, для любой пары функций
. И наоборот, для любой пары функций 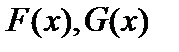 из множеств
из множеств 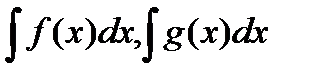 , их сумма
, их сумма  будет принадлежать множеству
будет принадлежать множеству 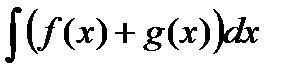 .
.
Таблица неопределенных интегралов
Из таблицы производных можно получить таблицу интегралов.
1) 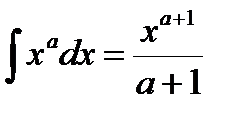 + С, a ¹ - 1.
+ С, a ¹ - 1.
2) 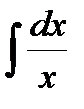 = ln| x | + С, X ={x>0} или X ={ x<0 }, но не на X =(-¥,0)È(0,¥) .
= ln| x | + С, X ={x>0} или X ={ x<0 }, но не на X =(-¥,0)È(0,¥) .
3)  + C, a¹1,
+ C, a¹1, 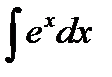 =ex+C.
=ex+C.
4) 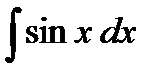 = - cos x + C,
= - cos x + C,  = sin x + C.
= sin x + C.
5)  ,
, 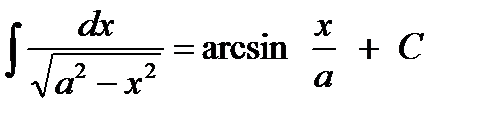 ,
, 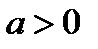 .
.
6) 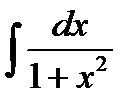 = arctg x + C,
= arctg x + C, 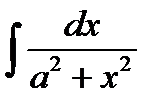 =
=  arctg
arctg 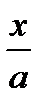 + C.
+ C.
7) 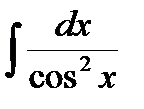 =tg x + C,
=tg x + C, 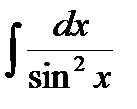 =- ctg x + C.
=- ctg x + C.
8) 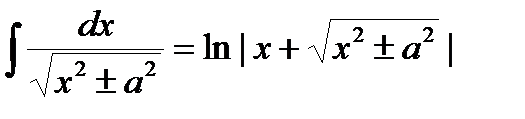 + C.
+ C.
9) 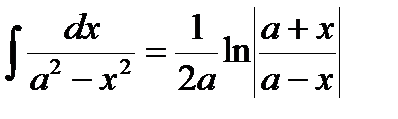 + C.
+ C.
10) 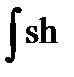 x dx = ch x + C,
x dx = ch x + C,  x dx = sh x + C.
x dx = sh x + C.
11) 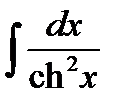 = th x + C ,
= th x + C , 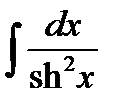 = -cth x + C .
= -cth x + C .
1.1.4. Замена переменного
Если F(x)– первообразная для f(x) на X т.е. 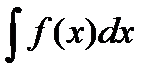 =F(x)+ C , функция x =j(t) дифференцируема на T и определена суперпозиция
=F(x)+ C , функция x =j(t) дифференцируема на T и определена суперпозиция 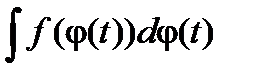 = F(j(t))+ C , тогда функция F(t)= f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,
= F(j(t))+ C , тогда функция F(t)= f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,
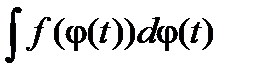 =
= 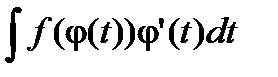 (формула замены переменного).
(формула замены переменного).
Для доказательства достаточно продифференцировать левую и правую части и убедиться, что получится одна и та же функция.
Примеры:
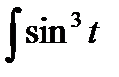 cos t dt =
cos t dt = 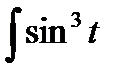 d sin t =
d sin t = 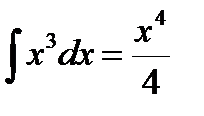 + C =
+ C = 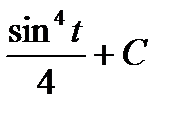 .
.
J = 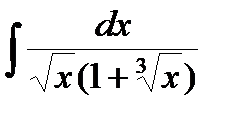 , сделаем замену x = t6, тогда
, сделаем замену x = t6, тогда
J=6  =6
=6 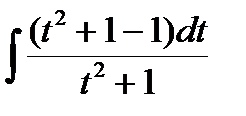 =6t – 6 arctg t + C =6
=6t – 6 arctg t + C =6 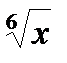 –6 arctg
–6 arctg 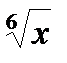 +C.
+C.
Интегрирование по частям
Если u(x), v(x) – дифференцируемы на отрезке X и существует
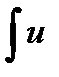 dv =
dv = 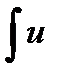 (x)v ¢(x)dx , тогда существует и интеграл
(x)v ¢(x)dx , тогда существует и интеграл 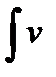 du и выполняется равенство
du и выполняется равенство
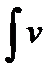 du = uv -
du = uv - 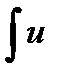 dv (формула интегрирования по частям).
dv (формула интегрирования по частям).
Доказательство. Пусть 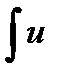 dv = F(x)+ C. Тогда функция uv – F будет первообразной для
dv = F(x)+ C. Тогда функция uv – F будет первообразной для 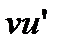 , что можно проверить дифференцированием:
, что можно проверить дифференцированием: 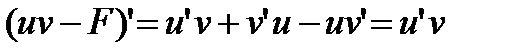 . Можно было продифференцировать левую и правую части и убедится, что получится одна и та же функция.
. Можно было продифференцировать левую и правую части и убедится, что получится одна и та же функция.
Пример. Для интеграла  x dx выберем функции: v(x) = ln x , u(x) = x , тогда
x dx выберем функции: v(x) = ln x , u(x) = x , тогда
 x dx =x ln x -
x dx =x ln x - 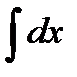 =x ln x – x + C.
=x ln x – x + C.
1.2. Разложение рациональной функции на простейшие дроби и их интегрирование
Разложение дроби на элементарные. Метод неопределенных коэффициентов.
Предварительные сведения из алгебры многочленов
а) Если a вещественный корень многочлена 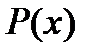 , то существует единственное представление многочлена в виде
, то существует единственное представление многочлена в виде
P(x ) = 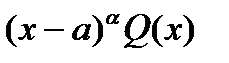 , a ³ 1, и
, a ³ 1, и  - многочлен, причем
- многочлен, причем  .
.
Число a называется кратностью корня. Другое эквивалентное определение кратности корня дается в терминах производных: a – это порядок первой, не равной нулю производной в точке a : P(a)= P ¢(a)=…= P(a-1)(a)=0, P(a)(a)¹0.
Доказательство этого свойства следует из формулы Тейлора для многочлена  . Действительно, пусть
. Действительно, пусть 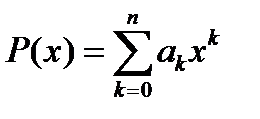 . Очевидно, что все производные этого многочлена, начиная с порядка
. Очевидно, что все производные этого многочлена, начиная с порядка 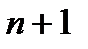 , будут тождественно равны нулю. Поэтому разложение функции
, будут тождественно равны нулю. Поэтому разложение функции 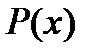 по формуле Тейлора в точке
по формуле Тейлора в точке 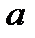 будет иметь вид (остаток в форме Лагранжа тождественно равен нулю)
будет иметь вид (остаток в форме Лагранжа тождественно равен нулю)
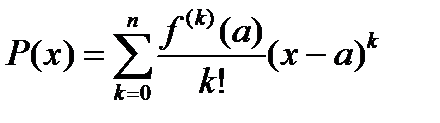 .
.
Если число 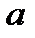 является корнем многочлена
является корнем многочлена 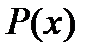 и
и 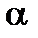 - порядок первой отличной от нуля производной
- порядок первой отличной от нуля производной  , то
, то
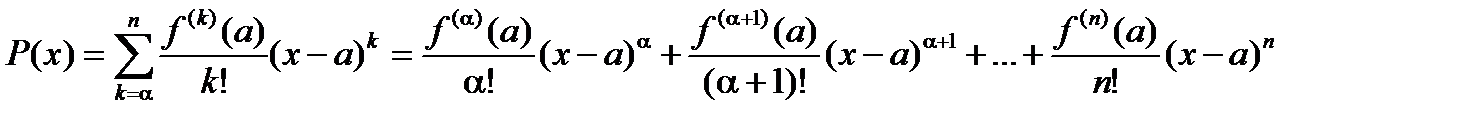 =
= 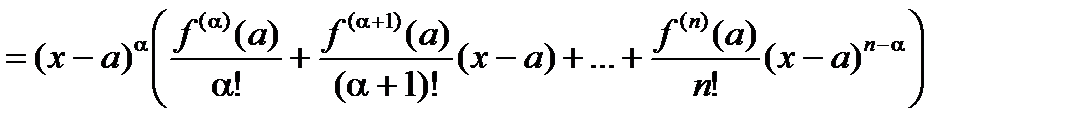 =
= 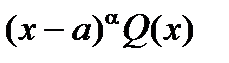 ,
,  .
.
б) Если z = u + i v , v¹0 комплексный корень многочлена с действительными коэффициентами, то сопряженное комплексное число  = u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения:
= u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения: 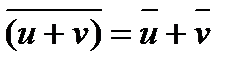 ,
, 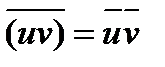 , для действительного числа x справедливо равенство
, для действительного числа x справедливо равенство 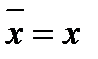 . Поэтому, если z корень многочлена P(x) = a0+…+ akxk +…+ anxn , то
. Поэтому, если z корень многочлена P(x) = a0+…+ akxk +…+ anxn , то 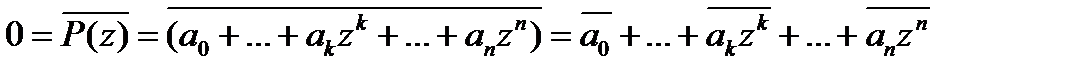 =
= 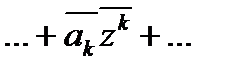 = =
= = 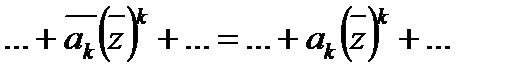 =P(
=P( 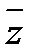 ).
).
Тогда существует единственное представление многочлена в виде
P(x) = (x2+px+q)b 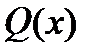 , b ³ 1, Q(z)¹0,
, b ³ 1, Q(z)¹0,
(x - z)(x - 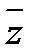 )=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
)=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
в) Любой многочлен можно разложить в произведение по своим корням
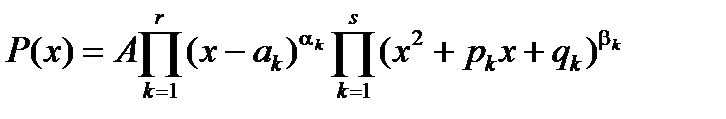 ,
,
где A – старший коэффициент многочлена, a1, a2,…, ar -действительные корни кратностей a1, a2,…, a r , а z1, z2,…, zs комплексные корни кратностей b1,b2,…, bs . Связь между комплексными корнями и сомножителями в разложении многочлена следующая x 2 + pkx + qk =(x - zk)(x - 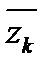 ).
).
Определение . Рациональная функция ( отношение двух многочленов) 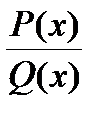 ) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
Утверждение. Любую рациональную функцию можно представить в виде многочлена (целая часть) плюс правильная дробь .
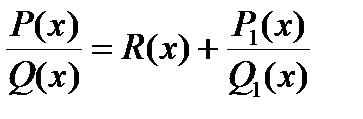 , - R ( x ) – многочлен, дробь
, - R ( x ) – многочлен, дробь 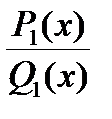 - правильная.
- правильная.
R(x) –называется целой частью, а дробь P1/Q1 –остатком. Остаток и целую часть можно получить делением «уголком».
Пример: Выделить целую и дробную часть 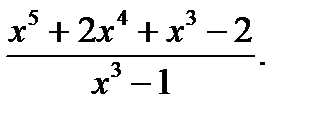
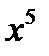
| 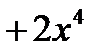
| 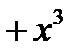
| 
| | ||||
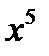
| 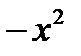
| | ||||||
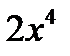
| 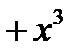
| 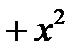
| 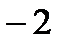
|
| ||||
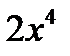
| 
|
| ||||||
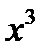
| 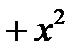
| 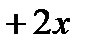
| 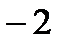
|
| ||||
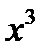
| 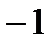
|
| ||||||

| 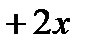
| 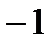
|
| |||||
Таким образом, 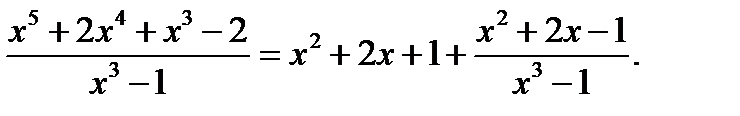
Определения
Пусть функция f(x) определена на [a , b]. Разбиением отрезка [a , b] называется набор точек D={a = x0< x1<…< xn =b}. Обозначим через x набор промежуточных точек для D, x={xk}, xk Î[xk , xk +1], k =0,1,…, n -1. Интегральной суммой для f , D и x называется выражение

Величина l(D)= 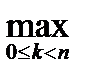 (xk +1 - xk) называется характеристикой разбиения D, точки xk называются узлами разбиения. Если промежуточные точки x={xk} выбраны для данного разбиения D (т.е. xkÎ[xk , xk+1]), то мы будем это обозначать знаком принадлежности xÎD.
(xk +1 - xk) называется характеристикой разбиения D, точки xk называются узлами разбиения. Если промежуточные точки x={xk} выбраны для данного разбиения D (т.е. xkÎ[xk , xk+1]), то мы будем это обозначать знаком принадлежности xÎD.
Определение. Предел интегральных сумм s(f ,D,x) при l(D)®0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется определенным интегралом от функции f на отрезке[a , b] и обозначается
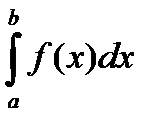 =
= 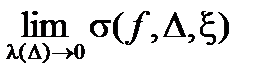 .
.
Более точно это определение выглядит следующим образом:
$J"e>0$d>0:(l(D)<d,xÎD) Þ |s(f ,D,x) - J |<e или
$J"e>0$d>0"D, l(D)<d,"xÎD : |s(f ,D,x) - J |<e.
Функция f(x), для которой существует интеграл 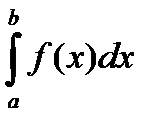 , называется интегрируемой (по Риману) на данном отрезке.
, называется интегрируемой (по Риману) на данном отрезке.
Пусть функция f(x) интегрируема на [a , b]. Выберем последовательность разбиений 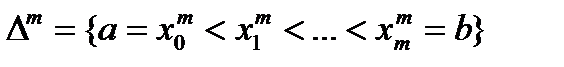 , с равноотстоящими узлами
, с равноотстоящими узлами 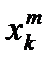 = a +
= a + 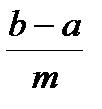 k , k =0,1,…, m. Тогда
k , k =0,1,…, m. Тогда 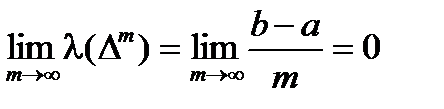 . Для каждого из этих разбиений будем считать заданным некоторый набор промежуточных точек
. Для каждого из этих разбиений будем считать заданным некоторый набор промежуточных точек 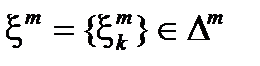 , например, можно выбирать средние точки
, например, можно выбирать средние точки 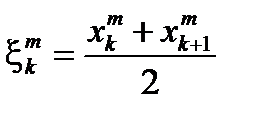 . Полученную таким образом последовательность интегральных сумм
. Полученную таким образом последовательность интегральных сумм
sm = s( f ,Dm ,xm)= 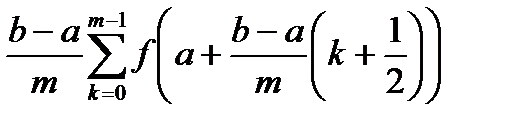 будем называть стандартной последовательностью интегральных сумм.
будем называть стандартной последовательностью интегральных сумм.
Из определения интеграла следует, что
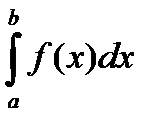 =
= 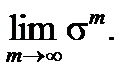
Таким образом, если функция 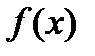 интегрируема и sm ее стандартная последовательность интегральных сумм, то
интегрируема и sm ее стандартная последовательность интегральных сумм, то
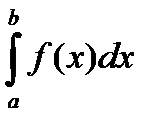 =
= 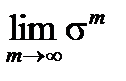 =
= 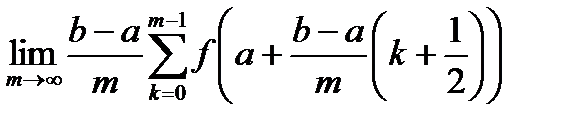 .
.
В качестве последовательности, реализующей значение интеграла можно брать суммы, где промежуточные точки совпадают с левыми или правыми концами отрезков разбиения. Например, для левых концов
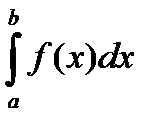 =
= 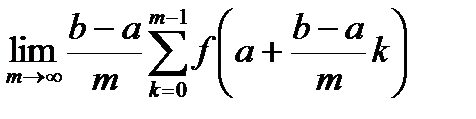 .
.
Формулы вычисления интегралов подобного вида называются квадратурными формулами.
Пример 1. Частный случай. Если функция f интегрируема на [0,1], то
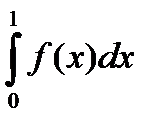 =
= 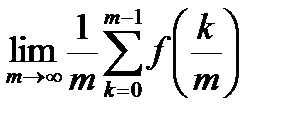 .
.
Пример 2. Вычислить предел 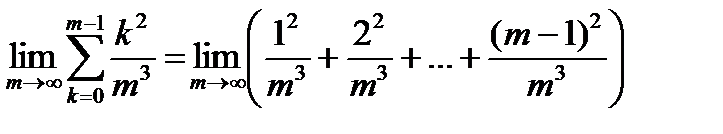 .
.
Суммы  является интегральными для функции
является интегральными для функции 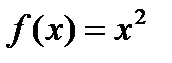 на отрезке
на отрезке 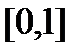 при выборе промежуточных точек, как в предыдущем примере, поэтому
при выборе промежуточных точек, как в предыдущем примере, поэтому
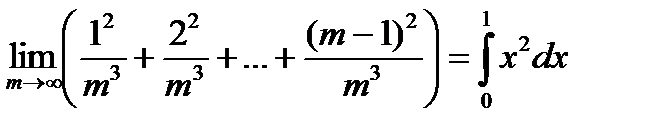 . В дальнейшем появятся формулы для вычисления интегралов. В нашем случае будет
. В дальнейшем появятся формулы для вычисления интегралов. В нашем случае будет 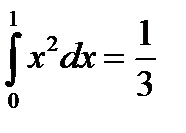 .
.
Теорема. Если функция интегрируема, то она ограничена.
Доказательство. Предположим противное, функция f(x) не ограничена на отрезке [a , b]. Тогда найдется последовательность t m Î[a , b], сходящаяся 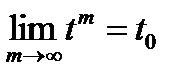 и такая, что
и такая, что 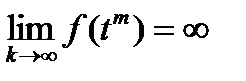 . Пусть e=1 для него
. Пусть e=1 для него
$d>0:(l(D)<d,xÎD) Þ |s(f ,D,x) - J |<1,
где 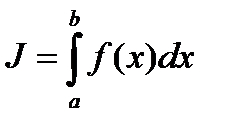 . Таким образом, если разбиение D имеет характеристику l(D)<d , то интегральная сумма s(f ,D,x) ограничена |s(f,D,x)|
. Таким образом, если разбиение D имеет характеристику l(D)<d , то интегральная сумма s(f ,D,x) ограничена |s(f,D,x)|  , не зависимо от выбора промежуточных точек
, не зависимо от выбора промежуточных точек  . С другой стороны любую интегральную сумму s(f ,D,x) можно сделать сколь угодно большой, выбрав подходящим образом лишь одну из промежуточных точек, полагая ее равной соответствующему члену последовательности
. С другой стороны любую интегральную сумму s(f ,D,x) можно сделать сколь угодно большой, выбрав подходящим образом лишь одну из промежуточных точек, полагая ее равной соответствующему члену последовательности  . Полученное противоречие завершает доказательство.
. Полученное противоречие завершает доказательство.
Свойства сумм Дарбу
Определение. Если разбиение D2 получено из разбиения D1 добавлением некоторого числа узлов, то говорят, что разбиение D2 следует за разбиением D1 (или D2 является более мелким, чем D1), при этом пишут D1 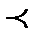 D2 .(см. слайд «Интегральные суммы»)
D2 .(см. слайд «Интегральные суммы»)
Интегральные суммы
1) Для любого разбиения D и набора промежуточных точек xÎD имеют место соотношения
s(f,D) £ s( f,D,x) £ S(f,D), s(f,D) = 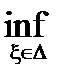 s( f,D,x), S(f,D) =
s( f,D,x), S(f,D) =  s( f,D,x).
s( f,D,x).
Это свойства следует непосредственно из определения интегральных сумм и сумм Дарбу.
2) Если D1 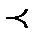 D2 два разбиения данного отрезка, то
D2 два разбиения данного отрезка, то
s(f ,D1) £ s(f ,D2) , S(f ,D2) £ S(f ,D1) .
Другими словами, при измельчении разбиения нижние суммы могут только увеличиться, а верхние суммы могут только уменьшиться.
Это утверждение достаточно доказать для случая, когда второе разбиение получено из первого добавление всего одной точки. Пусть новая точка появилась на отрезке [x¢k , x¢k+1]. Таким образом, во втором разбиении эта точка будет иметь номер k +1 и отрезоку [x¢k , x¢k+1] в первом разбиении будет соответствовать пара отнезков [x¢¢k , x¢¢k+1] , [x¢¢k+1, x¢¢k+2] во втором разбиении и [x¢k , x¢k+1] =[x¢¢k , x¢¢k+1] È[x¢¢k+1, x¢¢k+2]. См. рисунок 2.3 и слайд «Измельчение разбиения».
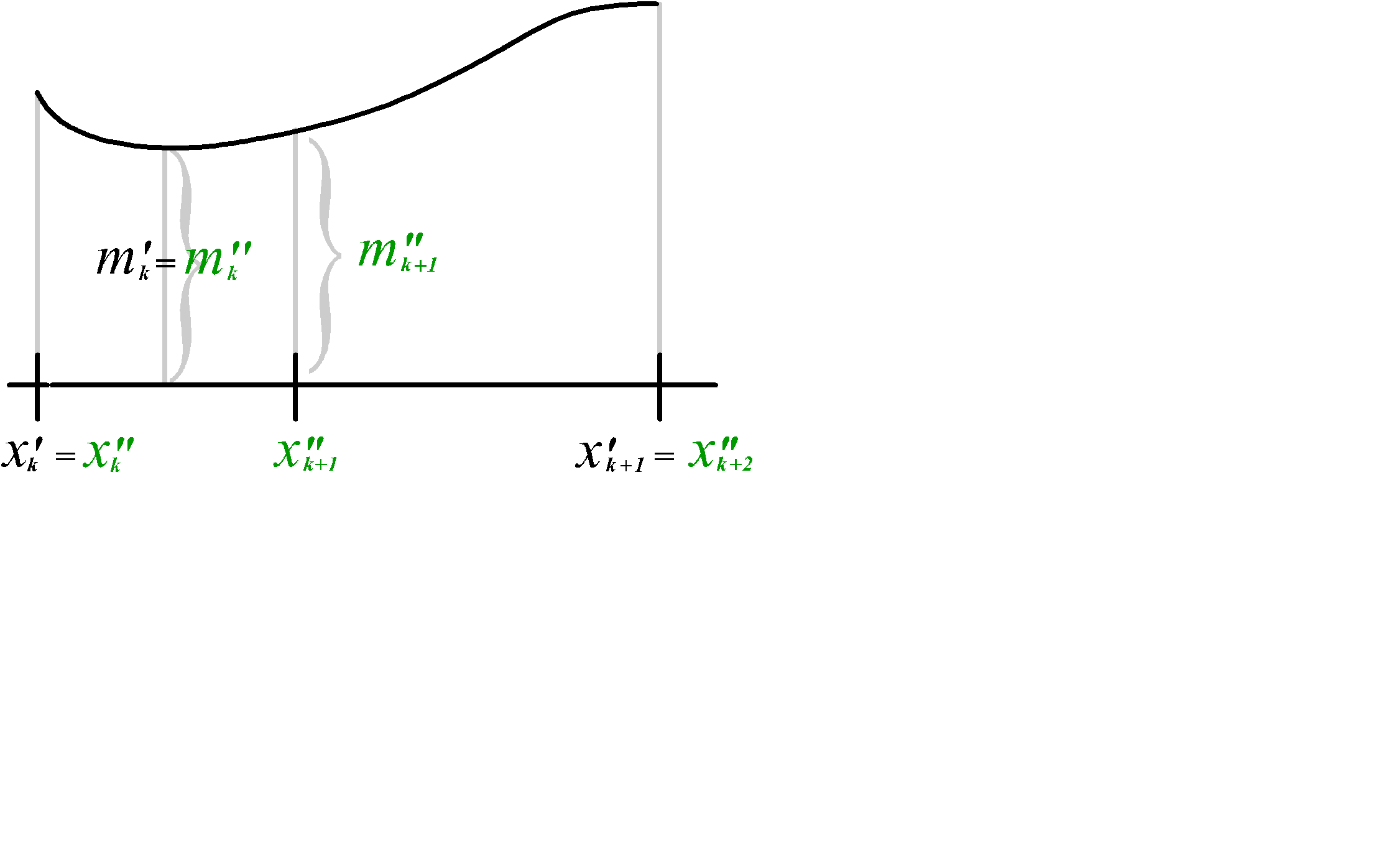
Рис. 2.3
Измельчение разбиения
Рассмотрим нижние суммы Дарбу. Нижняя грань функции по всему множеству [x¢k , x¢k+1] будет меньше или равна, чем нижняя грань по части этого множества, поэтому выполнены неравнства m¢k £ m¢¢k , m¢k £ m¢¢k+1. Отличие сумм s(f ,D1), s(f ,D2) состоит в том, что во второй сумме вместо слагаемого m¢k(x¢k +1 - x¢k) появились два слагаемых m¢¢k D¢¢k + m¢¢k+1 D¢¢k+1. Остальные слагаемые в обеих суммах будут одинаковыми.
Таким образом,
s(f ,D1) = A + m¢k D¢k +B,
s(f ,D2) = A+ m¢¢k D¢¢k + m ¢¢ k +1 D¢¢k+1 +B, следовательно
s(f,D2) - s(f,D1) = m¢¢k D¢¢k + m ¢¢ k+1 D¢¢k+1 - m¢k D¢k = m¢¢k D¢¢k + m¢¢k+1 D¢¢k+1 -
- m¢k (D¢¢k +D¢¢k+1) = (m¢¢k - m¢k) D¢¢k +( m¢¢k+1 - m¢k ) D¢¢k+1 ³ 0.
Здесь D¢k = x¢k+1 - x¢k = x¢¢k+2 - x¢¢k = x¢¢k+2 - x¢¢k+1 + x¢¢k+1 - x¢¢k = D¢¢k+1 +D¢¢k .
Аналогично доказывается утверждение для верхних сумм Дарбу.
3) Для любых разбиений D1 ,D2 данного отрезка справедливо неравенство
s(f ,D1) £ S(f ,D2).
Обозначим через D3 = D1 ÈD2 разбиение, образованное всеми узлами двух исходных разбиений. Очевидно D1  D3 , D2
D3 , D2  D3 . Тогда, как это следует из предыдущего свойства
D3 . Тогда, как это следует из предыдущего свойства
s(f ,D1) £ s(f ,D3) £ S(f ,D3) £ S(f ,D2),
откуда и следует доказываемое неравенство (см. слайд «Объединение разбиений»).
Объединение разбиений
2.1.5. Нижний и верхний интегралы
Определение. Колебанием функции f(x) на отрезке [xk,xk+1] будем называть величину
wk (f) = sup |f(x) – f(y)| = Mk – mk , где точная верхняя грань берется по всевозможным x, y из отрезка [xk,xk+1], mk = 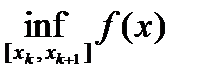 , Mk =
, Mk =  .
.
Отметим, что для разбиения D будет выполнено равенство (см. слайд «Нижние и верхние суммы Дарбу»)
S(f,D) - s(f,D) =  .
.
Нижние и верхние суммы Дарбу
Определение. Нижним интегралом  называется точная верхняя грань значений нижних сумм Дарбу
называется точная верхняя грань значений нижних сумм Дарбу 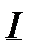 = sup s(f ,D), где верхняя грань берется по всевозможным разбиениям отрезка [a , b]. Аналогично определяется верхний интеграл
= sup s(f ,D), где верхняя грань берется по всевозможным разбиениям отрезка [a , b]. Аналогично определяется верхний интеграл 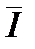 , как точная нижняя грань значений верхних сумм Дарбу
, как точная нижняя грань значений верхних сумм Дарбу 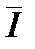 = inf S(f ,D), где точная грань берется по всевозможным разбиениям отрезка [a , b].
= inf S(f ,D), где точная грань берется по всевозможным разбиениям отрезка [a , b].
Для ограниченной функции существует, как нижний, так и верхний интегралы. Это следует из того, что множество значений нижних сумм Дарбу ограничено сверху, например, значением любой верхней суммы Дарбу. Множества верхних сумм Дарбу ограничено снизу, например, значением любой нижней суммой Дарбу.
Теорема. Для любого разбиения D данного отрезка справедливы неравенства
s(f ,D) £  £
£ 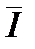 £ S(f ,D).
£ S(f ,D).
Доказательство. Не очевидным является только неравенство  £
£ 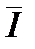 . Предположим противное, т.е., что
. Предположим противное, т.е., что 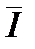 <
<  .
.
Выберем непересекающиеся e окрестности точек 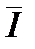 ,
,  , тогда
, тогда 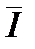 +e <
+e <  - e. По определениям точных граней найдутся два разбиения D1 , D2 такие, что S(f ,D1)<
- e. По определениям точных граней найдутся два разбиения D1 , D2 такие, что S(f ,D1)< 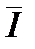 +e <
+e <  - e < s(f ,D2), что противоречит свойству 3) сумм Дарбу (Рис. 2.4, см. слайд «К доказательству теоремы»).
- e < s(f ,D2), что противоречит свойству 3) сумм Дарбу (Рис. 2.4, см. слайд «К доказательству теоремы»).
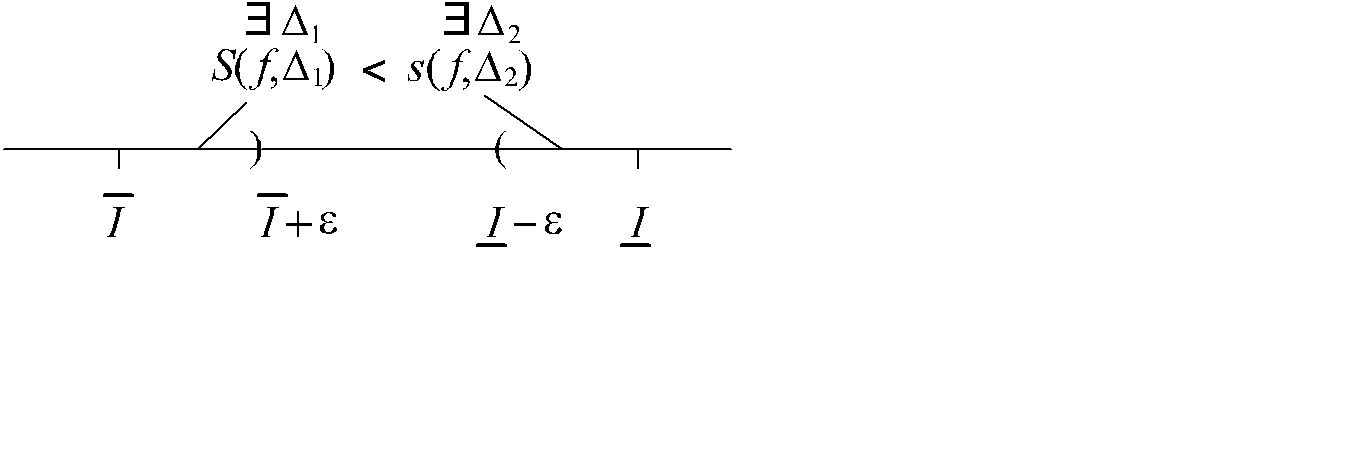
Рис. 2.4
К доказательству теоремы
2.1.6. Критерий интегрируемости. Теорема Дарбу
Теорема Дарбу. Для того, чтобы ограниченная функция была интегрируемой на отрезке [a,b], необходимо и достаточно, чтобы разность сумм Дарбу (см. слайд «Критерий интегрируемости»)
S(f ,D) - s(f ,D) ® 0 при l(D)®0. (2.1)
Критерий интегрируемости
То есть существование интеграла 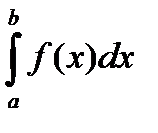 эквивалентно выполнению условие
эквивалентно выполнению условие
"e>0$d>0"D,l(D)<d: S ( f,D) - s(f,D)<e.
Доказательство. Необходимость. Пусть f(x) интегрируема и J = 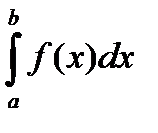 . Возьмем какое-либо e>0 для него $d>0 такое, что при l(D)<d будет выполнено неравенство
. Возьмем какое-либо e>0 для него $d>0 такое, что при l(D)<d будет выполнено неравенство
|s( f ,D,x)–J |<e/3 ( для любых xÎD ).
так как s(f ,D) = 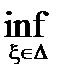 s( f ,D,x), S(f ,D) =
s( f ,D,x), S(f ,D) = 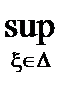 s( f ,D,x), то
s( f ,D,x), то
| S(f ,D) - J |≤ e /3, | J - s(f ,D)| ≤ e/3
тогда
|S(f,D) - s(f,D)|=|S(f,D) - J + J - s(f,D)| £ |S(f,D) - J| +| J - s(f,D)| £ 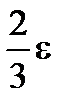 <e .
<e .
Достаточность. Разность сумм Дарбу может быть сделана сколь угодно малой выбором достаточно мелкого разбиения. Как уже отмечалось (2.1), нижний и верхний интегралы существуют и
s(f ,D) £ 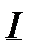 £
£ 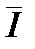 £ S(f ,D),
£ S(f ,D),
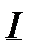 = sup s(f,D),
= sup s(f,D), 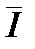 = inf S(f,D).
= inf S(f,D).
Так как 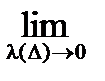 (S(f ,D) - s(f ,D)) = 0 , то
(S(f ,D) - s(f ,D)) = 0 , то 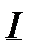 =
= 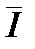 . Положим I =
. Положим I = 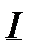 =
= 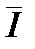 . Из условия (2.1) и неравенств s(f,D) £ s( f,D,x) £ S(f,D) следует, что |s(f ,D,x) – I | £ S(f ,D) - s(f ,D) (рис. 2.5).
. Из условия (2.1) и неравенств s(f,D) £ s( f,D,x) £ S(f,D) следует, что |s(f ,D,x) – I | £ S(f ,D) - s(f ,D) (рис. 2.5).
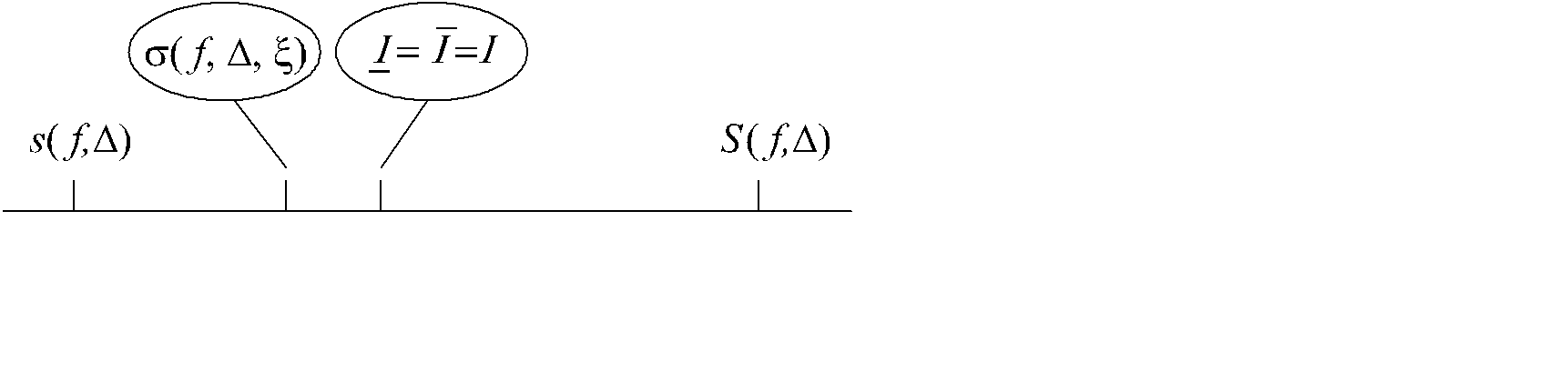
Рис. 2.5
Откуда и получается требуемое утверждение.
2.2. Классы интегрируемых функций, свойства определенного интеграла
Интегрируемость непрерывных функций и некоторых других классов функций. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.
2.2.1. Непрерывные функции
Теорема 1. Всякая непрерывная на отрезки [a , b] функция интегрируема на этом отрезке.
Доказательство. Как ранее отмечалось
S(f ,D) - s(f ,D) = 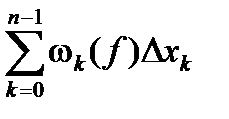 , wk (f) = Mk – mk .
, wk (f) = Mk – mk .
По теореме Кантора для любого e > 0 существует d > 0 такое, что при l(D)<d будет выполнено неравенство wk(f)< 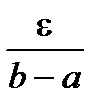 . Тогда
. Тогда
S(f ,D) - s(f ,D) = 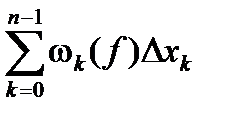 <
< 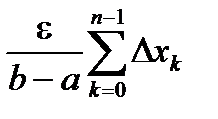 =e .
=e .
Интегрирование по частям
Теорема 2. Если функции u(x), v(x) непрерывны вместе со своими производными на [a , b], то
 dx =
dx =  –
– 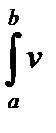 dx=
dx= 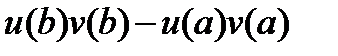 –
– 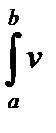 dx (2.5)
dx (2.5)
Доказательство.
 =
= 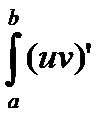 dx =
dx =  dx =
dx = 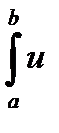 dv +
dv + 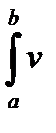 du .
du .
Откуда и следует формула (2.5).
Примеры


3.3. Вычислить  . Имеем
. Имеем 
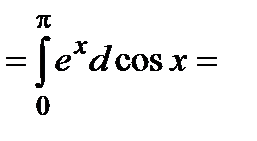
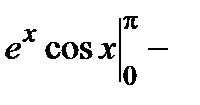
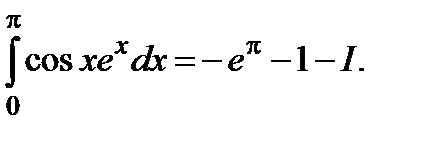 Откуда получим
Откуда получим 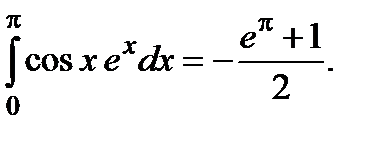
3.4. Вычислить 
 .
.

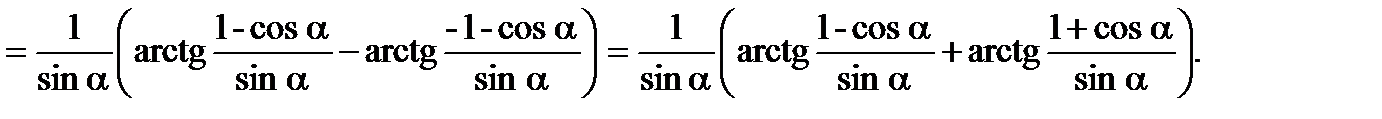
Если формально применить формулу  (в нашем случае 1-ab=0), то
(в нашем случае 1-ab=0), то 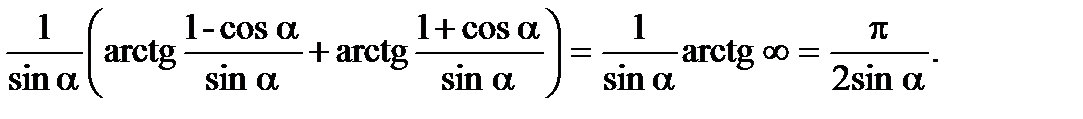 Законность этой операции можно обосновать.
Законность этой операции можно обосновать.
2.3.5. Остаточный член формулы Тейлора в интегральной форме
Пусть функция f(x) определена на отрезке [a , b] и имеет там непрерывные производные до порядка n +1. Тогда для всех x из [a , b] справедлива формула Тейлора с остатком в интегральной форме
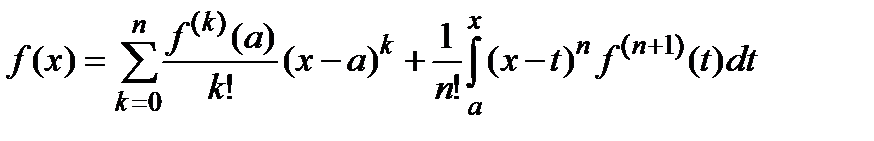 .
.
Доказательство. Обозначим остаток в формуле Тейлора Rn +1= 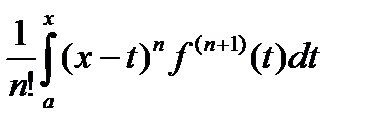 , Uk =
, Uk = 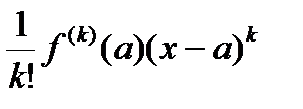 . Интегрируя по частям, получим
. Интегрируя по частям, получим
Rn+1= 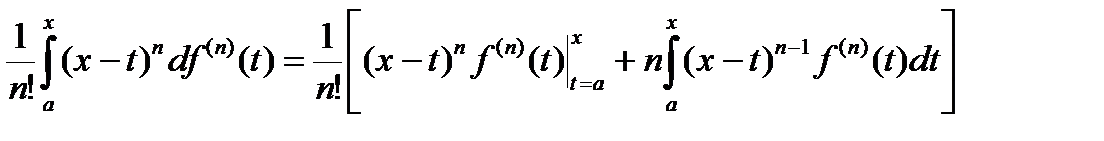 =
= 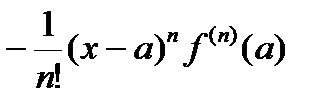 + Rn= =– Un+ Rn =– Un – Un-1+ Rn-1=…= –
+ Rn= =– Un+ Rn =– Un – Un-1+ Rn-1=…= –  + R1=
+ R1= 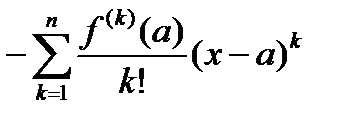 +
+ 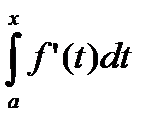 =
=  . Откуда и следует доказываемая формула.
. Откуда и следует доказываемая формула.
Длина дуги гладкой кривой
Ранее была доказана
Теорема. Если кривая
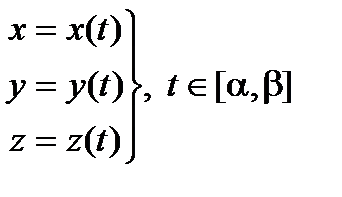
непрерывно дифференцируема, то длина ее дуги s(t) от начала кривой до точки с параметром t (рис. 2.9) является строго монотонно возрастающей, непрерывно дифференцируемой функцией и
 .
.
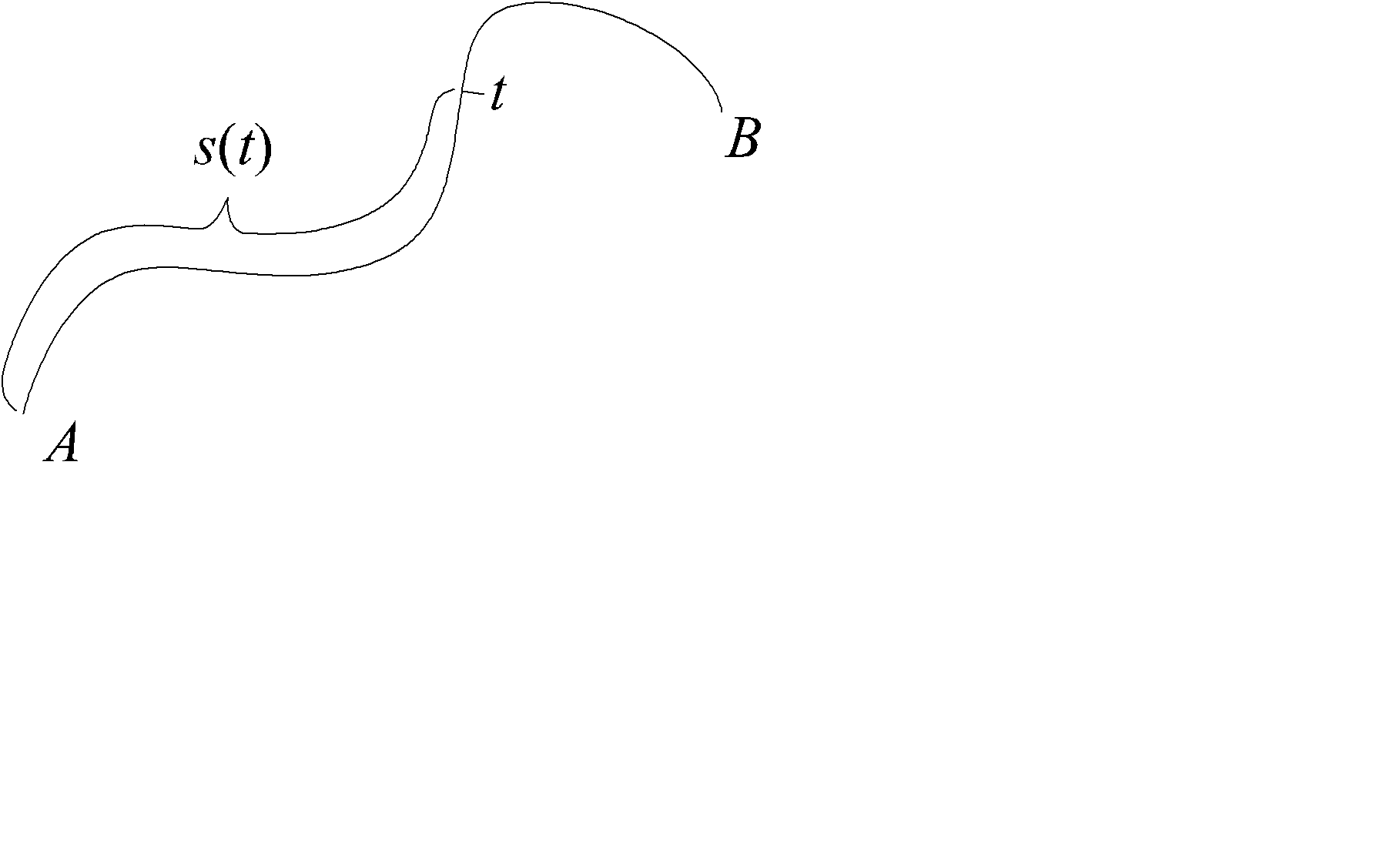
Рис. 2.9
Следствием является
Теорема. При условии непрерывной дифференцируемости длина кривой равна
s = 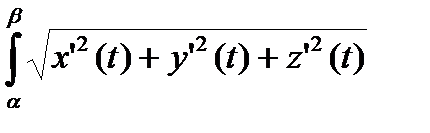 dt (2.6)
dt (2.6)

Рис. 2.10
Равенство (2.6) для длины кривой следует из предыдущей теоремы с помощью формулы Ньютона-Лейбница.
Замечание 1. В плоском случае
s =  dt .
dt .
Замечание 2. Если в качестве кривой рассматривается график функции f(x) на отрезке [a , b], то эту кривую можно параметризовать 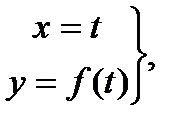 tÎ[a , b] и ее длина будет вычисляться по формуле s =
tÎ[a , b] и ее длина будет вычисляться по формуле s = 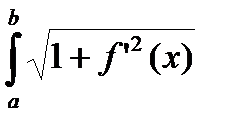 dx .
dx .
Рис. 2.11
Замечание 3. Для графика функции, заданной в полярных координатах r(j), jÎ[a,b] длина кривай будет равна
s =  dj.
dj.

Рис. 2.12
Для вывода этой формулы следует рассмотреть параметризацию кривой
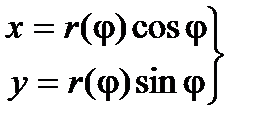 , jÎ[a,b].
, jÎ[a,b].
Примеры.
1.1. Вычислить длину кривой  , y =ln cos x ,
, y =ln cos x ,  .
.
Длина кривой будет равна 
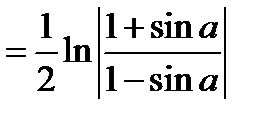 .
.
1.2. Вычислить длину астроиды x2/3+ y2/3= a2/3.(рис. 2.13, слайд «Астроида»)

Рис. 2.13
Астроида
В парметрическом виде уравнение астроиды имеет вид 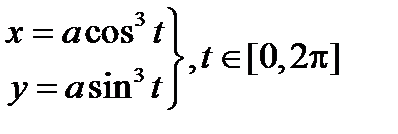 . Вычислим производные и подинтегральную функцию для нахождения длины дуги кривой, расположенной в первом квадранте :
. Вычислим производные и подинтегральную функцию для нахождения длины дуги кривой, расположенной в первом квадранте :
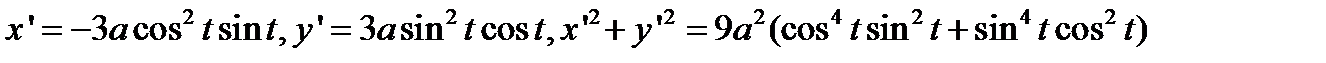 ,
, 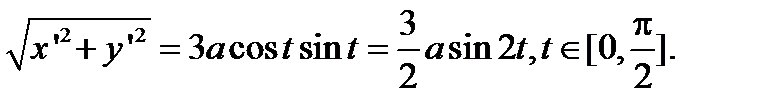 Длина всей дуги будет равна
Длина всей дуги будет равна

 2.4. Площадь плоской области
2.4. Площадь плоской области
Квадрируемость. Криволинейна трапеция. Области с границей в полярных координатах
Квадрируемые фигуры
Многоугольником P в этом параграфе называется внутренняя часть области, ограниченной замкнутой не самопересекающейся ломаной L . Для упрощения формулировок, объединение конечного числа многоугольников будет также называться многоугольником (см рис. 2.14).
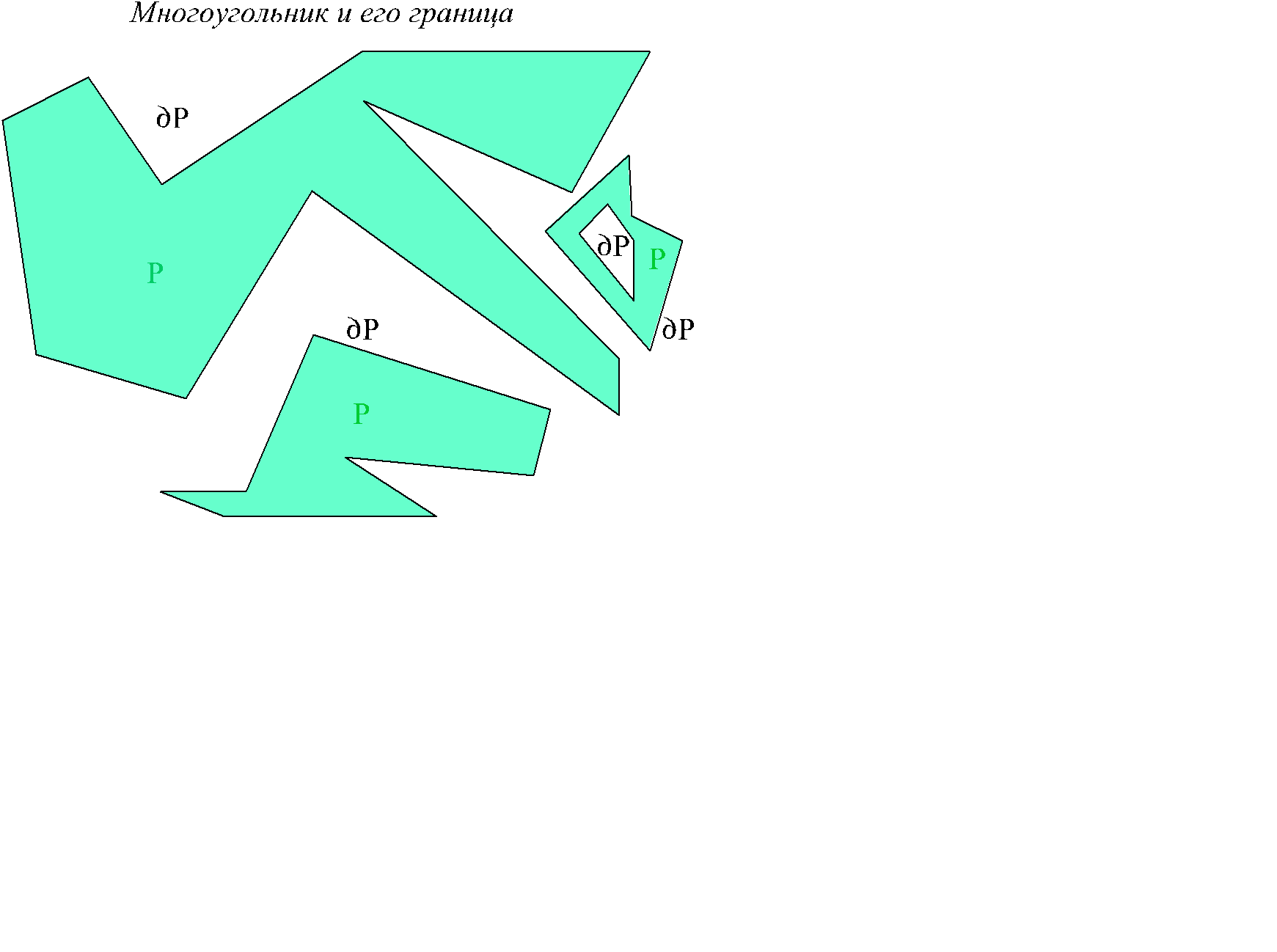
Рис. 2.14
Сама ломаная L (или ломаные) называется границей многоугольника P и обозначается ¶P . Многоугольник плюс граница обозначается  = P +¶P (замыкание области). Для области, показанной на рисунке, граница состоит из двух замкнутых ломаных. Будем предполагать известным понятие площади для многоугольников (эта площадь находится триангуляцией, разбиением области на треугольники Рис. 2.15).
= P +¶P (замыкание области). Для области, показанной на рисунке, граница состоит из двух замкнутых ломаных. Будем предполагать известным понятие площади для многоугольников (эта площадь находится триангуляцией, разбиением области на треугольники Рис. 2.15).
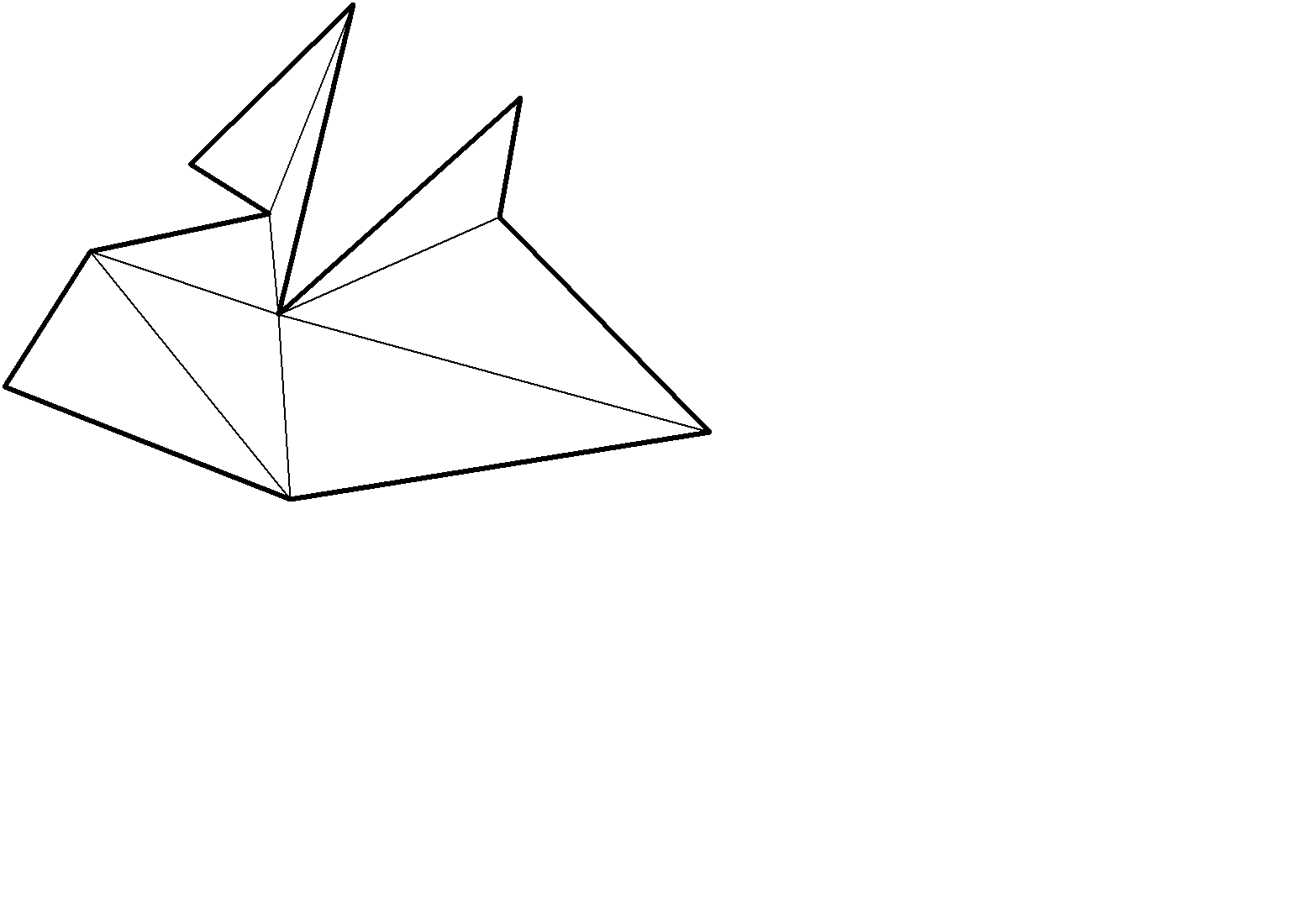
Рис. 2.15
Под областью в этом параграфе будем понимать ограниченное множество, для которого существует хотя бы один вписанный многоугольник. Кроме того, мы в дальнейшем будем рассматривать только множества, ограниченные одной или несколькими замкнутыми кривыми.
Определение. Индексом i будем обозначать многоугольники, вписанные в заданную область D , Pi Ì Dȶ D ( ¶ D – кривая, ограничивающая область D ). Индексом e будем обозначать описанные многоугольники, Pe É Dȶ D . Площадь многоугольника P будем обозначать через mP (см. слайд «Вписанные и описанные многоугольники»).
Вписанные и описанные многоугольники
Для площади многоугольников известно свойство монотонности: если PÌQ , то mP £ mQ .
Определение. Нижней площадью области D назовем величину mD = sup mPi , где точная верхняя грань берется по всевозможным вписанным многоугольникам.
Верхней площадью области D назовем величину  = inf mPe , где точная нижняя грань берется по всевозможным описанным многоугольникам.
= inf mPe , где точная нижняя грань берется по всевозможным описанным многоугольникам.
Как уже отмечалось, мы будем рассматривать лишь ограниченные области, для которых множество вписанных многоугольников не пусто. В этом случае верхние и нижние площади будут существовать.
Лемма. mD £ 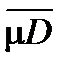 .
.
Доказательство. От противного. Пусть 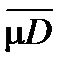 £ mD (см. слайд «Неравенство между нижней и верхней площадью»).
£ mD (см. слайд «Неравенство между нижней и верхней площадью»).
Неравенство между нижней и верхней площадью
Выбираем непересекающиеся окрестности чисел  , mD . По определению нижней и верхней площадей найдутся два многоугольника Pi , Pe , один с площадью mPe из выбранной окрестности числа
, mD . По определению нижней и верхней площадей найдутся два многоугольника Pi , Pe , один с площадью mPe из выбранной окрестности числа 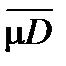 , другой с площадью из окрестности числа mD . Согласно выбору окрестностей mPe < mPi , что противоречит свойству монотонности площадей для многоугольников.
, другой с площадью из окрестности числа mD . Согласно выбору окрестностей mPe < mPi , что противоречит свойству монотонности площадей для многоугольников.
Следствие. Для любых Pi , Pe выполняется mPi £ mD £ 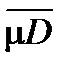 £ mPe .
£ mPe .
Определение. Область D называется квадрируемой, если 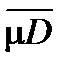 = mD . Эта общая величина называется площадью и обозначается mD .
= mD . Эта общая величина называется площадью и обозначается mD .
Теорема (критерий квадрируемости). Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы для любого e>0 существуют два многоугольника (описанный и вписанный) Pe , Pi такие, что mPe - mPi <e .
Доказательство. Как уже отмечалось для любых Pe , Pi выполняются неравенства
mPi £ mD £ 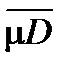 £ mPe ,
£ mPe ,
откуда и следует требуемое утверждение.
Следствие . Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы существовали две последовательности многоугольников 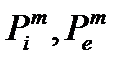 , такие, что
, такие, что  .
.
Замечание. Для многольников, указанных в этом следствии , справедливы равенства 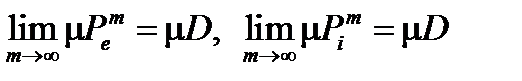 .
.
Определение. Множество D имеет площадь 0, если его можно покрыть многоугольниками со сколь угодно малой суммарной площадью.
Если область D имеет границу ¶D, то для квадрируемости D необходимо и достаточно, чтобы ¶D имела площадь равную нулю.
Если многоугольники Pe и Pi имеют разность площадей mPe - mPi < 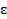 , то область Pe \Pi (полоса между ломаными, ограничивающими многоугольники Pe , Pi ) имеет площадь m (Pe \Pi )<
, то область Pe \Pi (полоса между ломаными, ограничивающими многоугольники Pe , Pi ) имеет площадь m (Pe \Pi )< 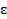 и содержит границу области D. Справедливо и обратное утверждение. Если многоугольник Q с площадью m (Q )<
и содержит границу области D. Справедливо и обратное утверждение. Если многоугольник Q с площадью m (Q )< 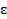 покрывает границу области D, то из его границ можно собрать границы двух многоугольников Pe и Pi с разностью площадей mPe - mPi <
покрывает границу области D, то из его границ можно собрать границы двух многоугольников Pe и Pi с разностью площадей mPe - mPi < 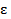 (без доказательства).
(без доказательства).
Свойства площади
Теорема (Монотонность). Если D1, D2 квадрируемы и D1Ì D2 , то mD1 £ mD2 (см. слайд «Свойство монотонности площади»).
Свойство монотонности площади
Доказательство. Любой Pi для D1 является вписанным и для D2, поэтому mD1=sup mPi будет £ m D2 (для области D2 площадь находится как верхняя грань площадей вписанных многоугольников по большему множеству).
Теорема (Аддитивность). Если квадрируемая область D разбита кусочно-гладкой кривой на две подобласти D1 , D2 , то они квадрируемы и
mD = mD1 + mD2.
Доказательство (только для ломаной, разбивающей область на две части). Обозначения см. слайд «Обозначения».
Обозначения
Выполнены следующие соотношения
Pi¢¢È Pi¢= Pi , Pe¢¢È Pe¢= Pe (2.7)
По заданному e выберем Pi , Pe так, что m Pe - m Pi < e . Из (2.7) следует, что
mPi¢¢ + mPi¢= mPi , mPe¢¢+ mPe¢= mPe . Вычитая из второго равенства первое получим , (mPe¢¢ - mPi¢¢) + (mPe¢ - mPi¢)= mPe - mPi < e . Откуда получаем неравенства (mPe¢¢ - mPi¢¢) < e , (mPe¢ - mPi¢) < e . Таким образом, квадрируемость D1 , D2 доказана. Для доказательства равенства mD = mD1 + mD2 отметим, что любой вписанный в D многоугольник Pi разбивается секущей ломаной на два вписанных многоугольника Pi¢¢È Pi¢= Pi для D1 , D2 . Поэтому mD =sup mPi £ mD1 +mD2. Точно также любой описанный многоугольник Pe распадается на два описанныхPe¢¢ÈPe¢= Pe . Поэтому будет выполнено обратное неравенство
mD =inf mPe³ mD1 +mD2.
Откуда и следует требуемое равенство.
В качестве еще одного свойства площади отметим ее независимость от выбора системы координат.
Теорема (Второй критерий квадрируемости). Пусть D некоторая область. Если для
"e>0 $ кадрируемые 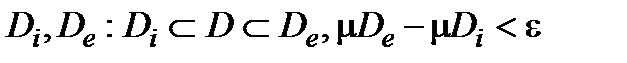 , то D квадрируема (см. слайд «Второй критерий квадрируемости»).
, то D квадрируема (см. слайд «Второй критерий квадрируемости»).
Второй критерий квадрируемости
В теореме сформулировано только достаточное условие квадрируемости, необходимость этого условия очевидна.
Доказательство. Возьмем 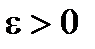 . Для него найдутся
. Для него найдутся  . В свою очередь для
. В свою очередь для 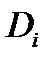 существует вписанный
существует вписанный 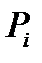 с такой площадью, что
с такой площадью, что 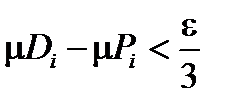 . Аналогично, для
. Аналогично, для  найдется описанный
найдется описанный 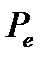 такой что
такой что  . Тогда
. Тогда
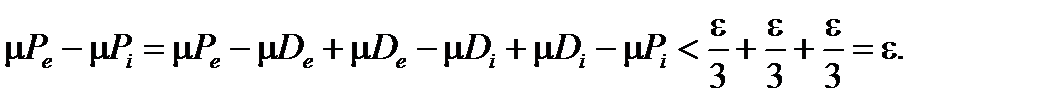
Так же как и для случая многоугольников, можно сформулировать
Следствие . Для того, чтобы ограниченная область D была квадрируемой необходимо и достаточно, чтобы существовали две последовательности квадрируемых областей 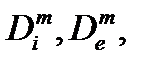 такие, что
такие, что 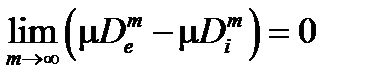 (см. слайд «Критерий квадрируемости в терминах границы»).
(см. слайд «Критерий квадрируемости в терминах границы»).
Критерий квадрируемости в терминах границы
2.4.3.Площадь криволинейной трапеции
Пусть f(x)³0 и непрерывна на отрезке [a , b]. Область расположенная между графиком функции f(x), осью x и вертикалями x = a , x = b называется криволинейной трапецией (см. слайд «Площадь криволинейной трапеции» ).
Площадь криволинейной трапеции
Теорема. Криволинейная трапеция D квадрируема и ее площадь
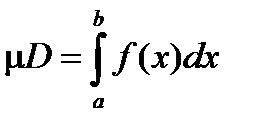 .
.
Доказательство. Пусть e>0. В силу интегрируемости f(x) для этого e существует разбиение отрезка [a , b], D={a = x0< x1<…< xn} такое, что S(f ,D) – s(f,D) < e . Прямоугольники, соответствующие нижней сумме Дарбу образуют вписанный в область D многоугольник Pi . Прямоугольники, соответствующие верхней сумме Дарбу образуют описанный многоугольник Pe для области D (Рис. 2.16), s(f ,D) = m Pi , S(f,D)= m Pe .
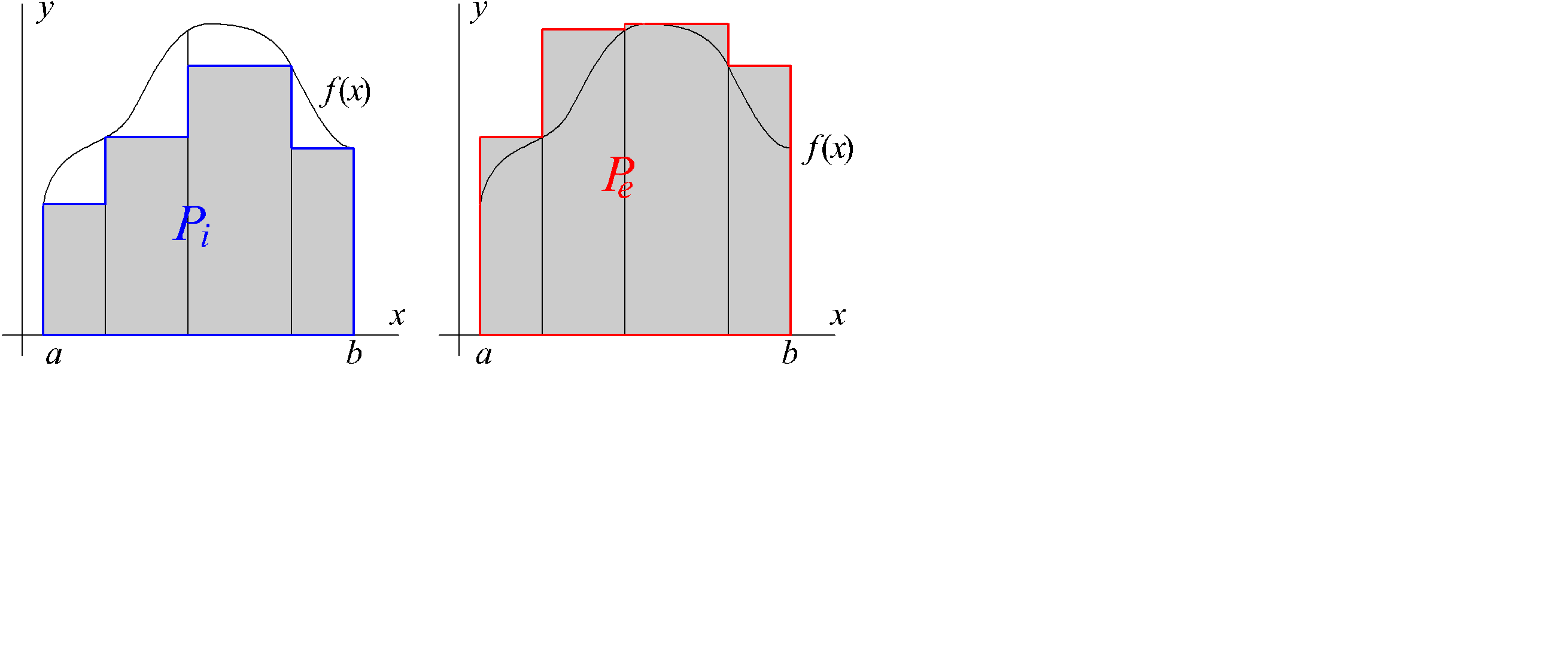
Рис. 2.16
Отсюда следует квадрируемость области D . Для доказательства равенства 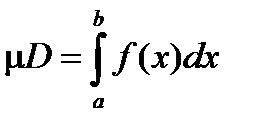 рассмотрим последовательность разбиений
рассмотрим последовательность разбиений  отрезка
отрезка  с равноотстоящими узлами. Соответствующие вписанные и описанные многоугольники обозначим
с равноотстоящими узлами. Соответствующие вписанные и описанные многоугольники обозначим  . Тогда, как уже упоминалось ранее, между суммами Дарбу и площадями многоугольников существует следующая связь
. Тогда, как уже упоминалось ранее, между суммами Дарбу и площадями многоугольников существует следующая связь 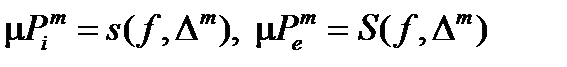 . Далее
. Далее  и
и 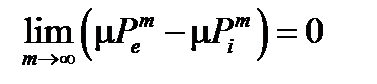 . Эти равенства позволяют утверждать (следствие из критерия интегрируемости), что
. Эти равенства позволяют утверждать (следствие из критерия интегрируемости), что 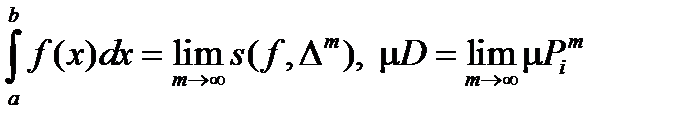 . Таким образом,
. Таким образом,  .
.
Замечание. Если f(x)£ 0 и непрерывна на отрезке [a , b], то 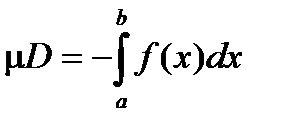 . Для области
. Для области
D , заключенной между двумя непрерывными кривыми (графиками функций) y = f1(x),
y=f2(x), f1(x)£ f2(x) на [a,b], 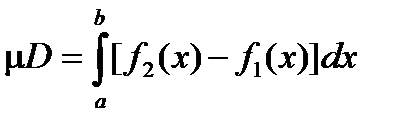 (рис 2.17).
(рис 2.17).

| 
|
| Рис. 2.17 | |
В более общих случаях для вычисления площади следует разбить область на фигуры указанного вида.
Объем
Понятие объема вводится аналогично тому, как это делалось для площади, поэтому похожие моменты в этом параграфе будут излагаться конспективно. Известным считается понятие объема элементарной области, т.е. для области, ограниченной многогранником (сводится к объему тетраэдра, не обязательно правильного). В дальнейшем эту область так же будем называть многогранником. Объединение конечного числа непересекающихся многогранников также будет называться многогранником (рис. 2.27).
Рис. 2.27
Далее рассматривается класс пространственных областей, которые ограничены (содержаться в некотором шаре) и для которых существует хотя бы один вписанный многогранник. Вписанные многогранники будем обозначать Pi описанные Pe . Объем обозначается mP. Объем обладает свойством монотонности, таким образом, всегда mPi £ mPe .
Нижний объем: mD = sup mPi , где точная грань берется по всевозможным вписанным многогранникам.
Верхний объем: 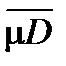 = inf mPe , где точная грань берется по всевозможным описанным многогранникам.
= inf mPe , где точная грань берется по всевозможным описанным многогранникам.
Аналогично тому, как это делалось площадей, доказывается неравенство mD £ 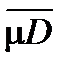 .
.
Определение. Область называется кубируемой, если совпадают нижний и верхний объемы 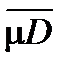 = mD . Эта общая величина называется объемом и обозначается mD.
= mD . Эта общая величина называется объемом и обозначается mD.
Теорема (Критерий кубируемости). Для того, чтобы область D была кубируемой необходимо и достаточно, чтобы "e>0$ Pe , Pi : mPe - mPi <e .
Теорема (Второй критерий кубируемости). Для того, чтобы область D была кубируемой необходимо и достаточно, чтобы "e>0$ кубируемые области De , Di (не обязательно многогранники) такие, что mDe - mDi <e .
Для объема справедливы свойства монотонности, аддитивности.
Пример. Цилиндр является кубируемым телом, если в его основании лежит квадрируемая фигура и его объем равен Sh (рис. 2.28).
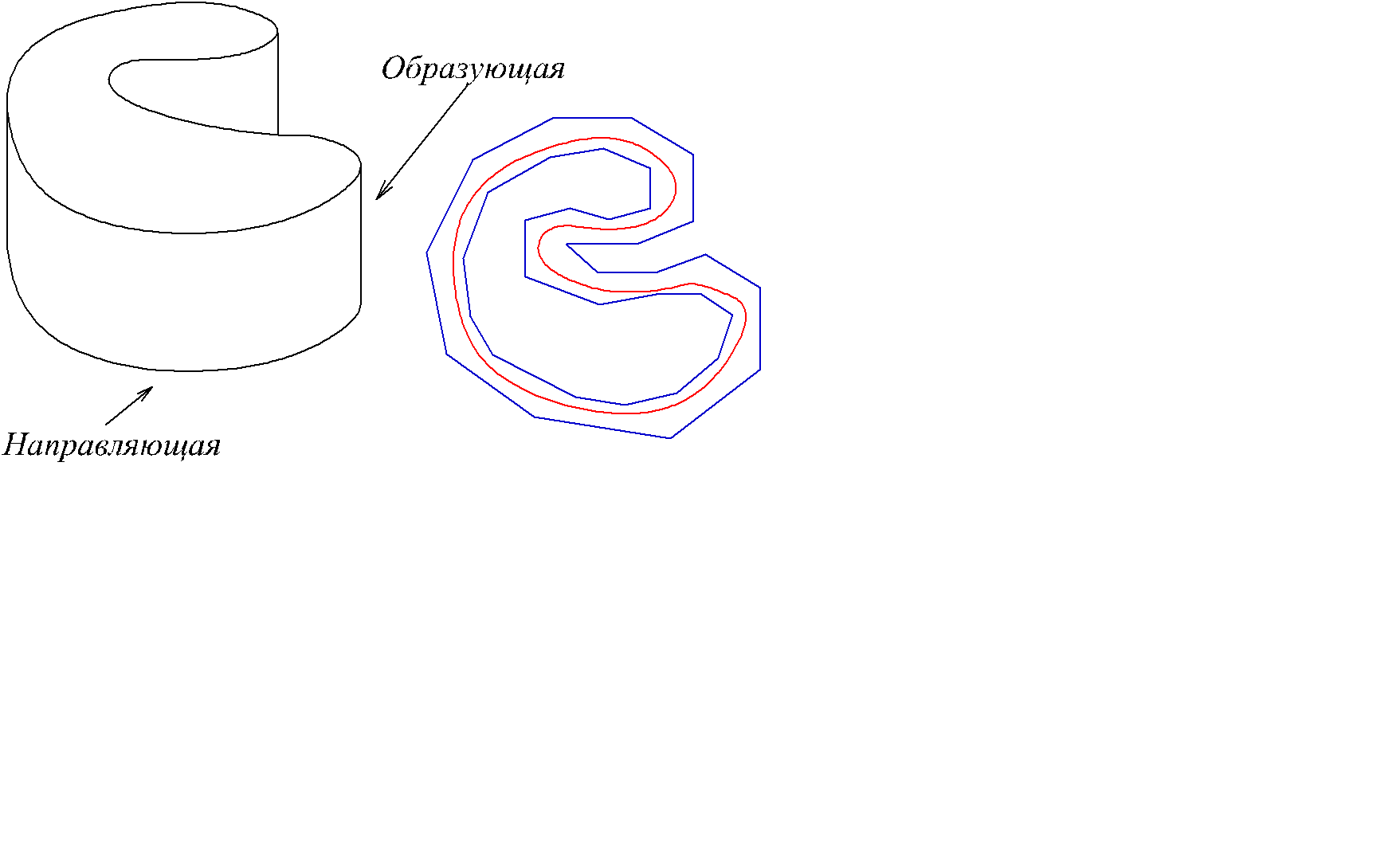
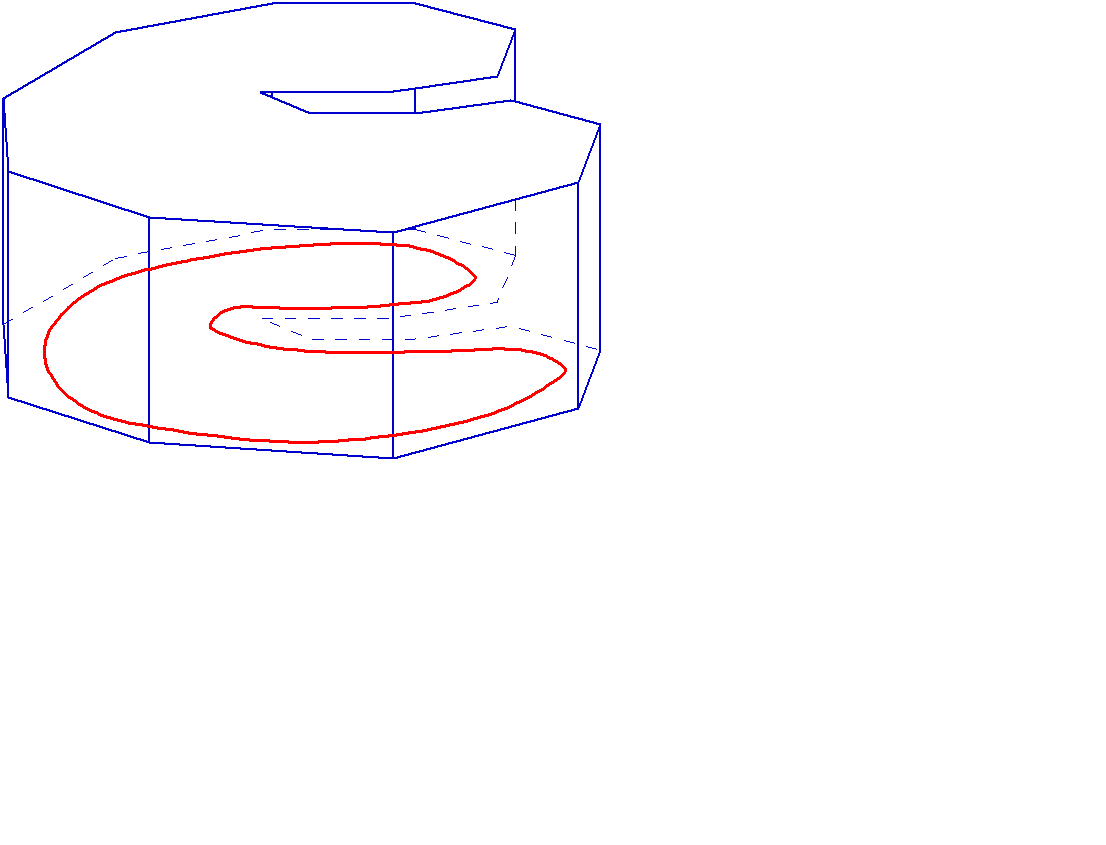
Рис. 2.28
Это следует из критерия кубируемости. В качестве вписанных и описанных многогранников выбираются призмы с той же образующей, что и у цилиндра, в основании которых лежат вписанные и описанные многоугольники для фигуры, лежащей в основании цилиндра.
В частности кубируемым будет «ступенчатое тело» (рис. 2.29), если в основании каждой составляющей лежит квадрируемая фигура.
Рис. 2.29
Объем тела вращения
Теорема. Если f(x)³ 0 непрерывна на [a , b] , то тело, граница которого, полученна вращением графика функции вокруг оси x (рис. 2.30, слайд «Тело вращения»), кубируемо и его объем равен
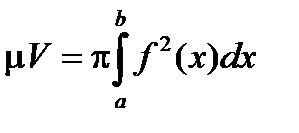
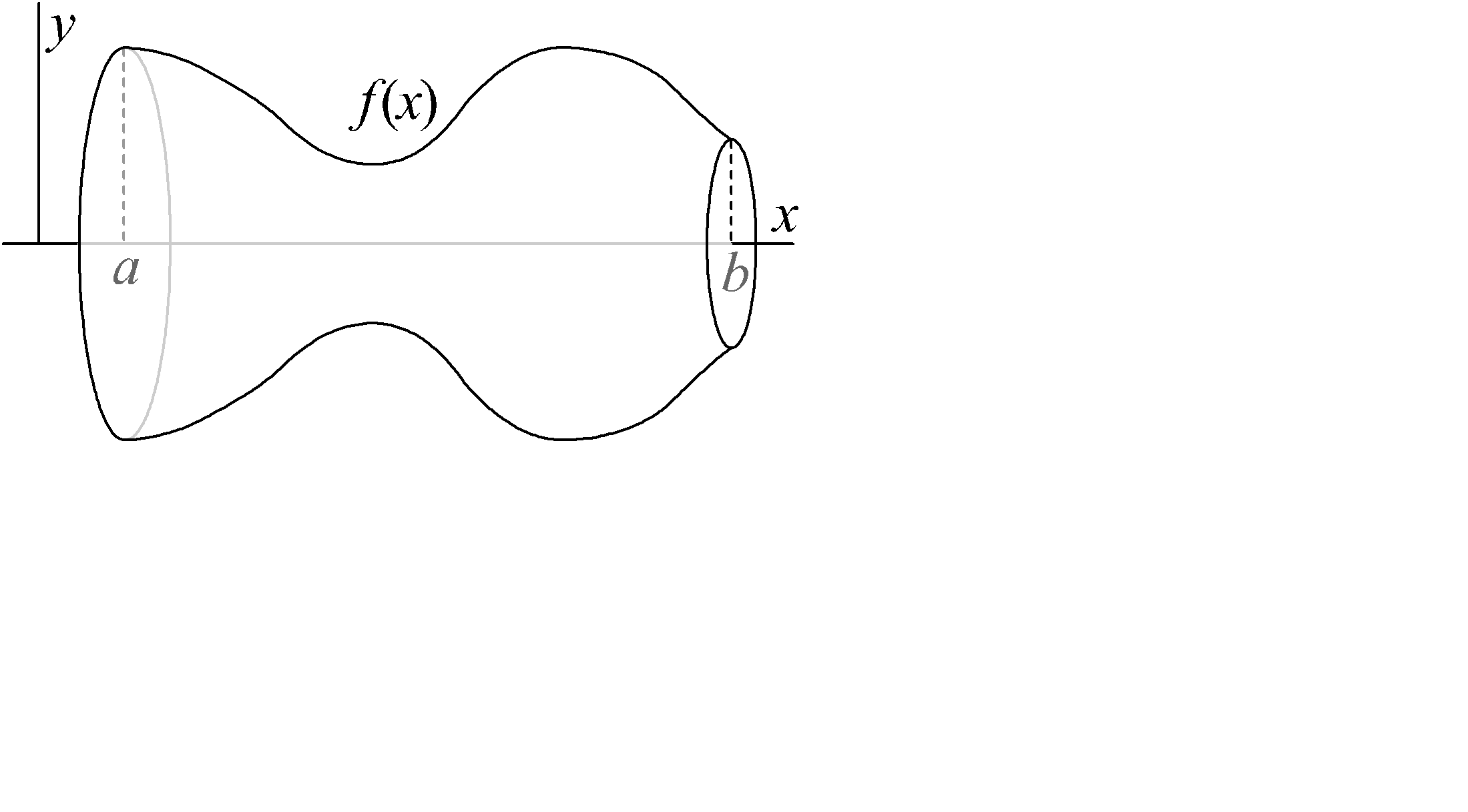
Рис. 2.30
Тело вращения
Доказательство. Для заданного e рассмотрим достаточно мелкое разбиение D={a = x0< x1<…< xn = b} и два ступенчатых тела на основании сумм Дарбу исходной функции, составленных из круговых цилиндров высотой xk +1 - xk и радиусов mk =  , Mk =
, Mk =  (Рис. 2.31). Объем этих тел будут равны s(F ,D), S(F ,D), где F(x)=p f 2(x) .
(Рис. 2.31). Объем этих тел будут равны s(F ,D), S(F ,D), где F(x)=p f 2(x) .
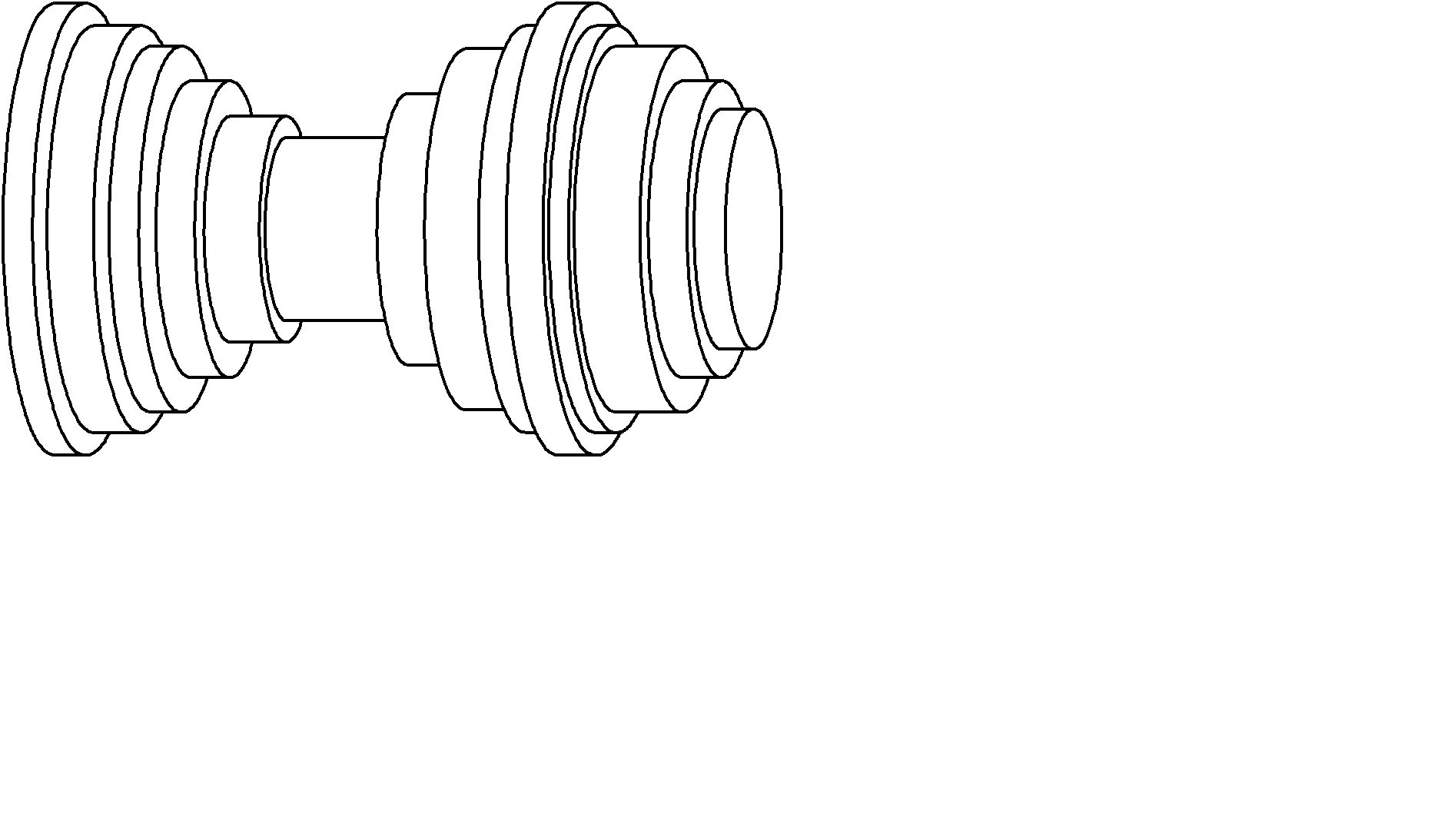
Рис. 2.31
Одна из этих кубируемых областей будет вписана в тело вращения, а другая описана. Разность объемов можно сделать сколь угодно малой, что следует из интегрируемости функции F(x).
Справедлива более общая теорема (без доказательства).
Теорема. Если область D проектируется на отрезок [a , b] оси x и любое сечение этой области плоскостью перпендикулярной оси x квадрируемо (рис. 2.32), а площадь этого сечения S(x) является интегрируемой функцией, то исходная область кубируема и ее объем равен
mD = 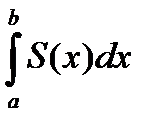
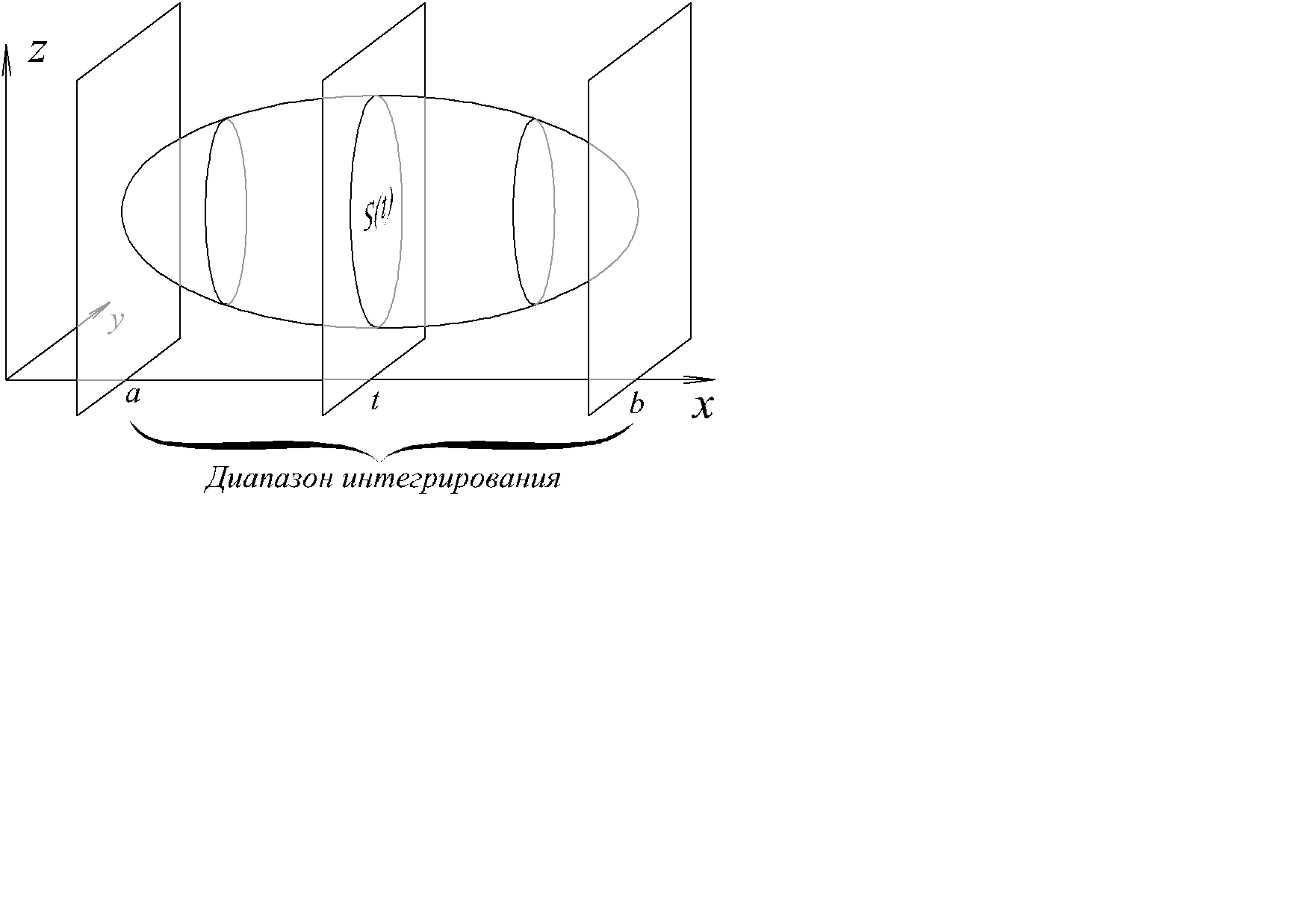
Рис. 2.32
Первая теорема Гюльдена
Предположим, что масса mk расположена на расстоянии yk от оси ox (рис. 2.39). Статический момент материальной точки массы m относительно оси ox равен yk mk . Статические моменты системы из n точек относительно осей ox , oy равны
Mx =  , My =
, My = 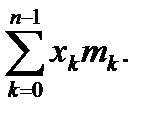
Рис. 2.39
Центр тяжести системы – это точка, обладающая следующим свойством: если в эту точку поместить сосредоточенную массу системы, то статический момент этой точки относительно любой оси совпадает со статическим моментом всей системы относительно этой оси. Выпишем равенство статических моментов дискретной системы относительно осей ox , oy .
XM = 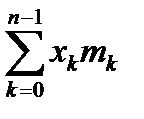 , YM =
, YM = 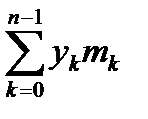 , M =
, M = 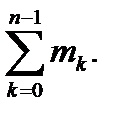
Тогда для координат центра тяжести системы получис выражения
X =  , Y =
, Y =  (2.13)
(2.13)
Если масса распределена вдоль кривой g :x = x(s), y = y(s), параметризованной длиной дуги и имеющей линейную плотность распределения массы r(s), то соотношения (2.13) для координат центра тяжести примут интегральный вид
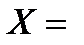
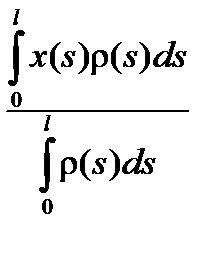 , Y =
, Y = 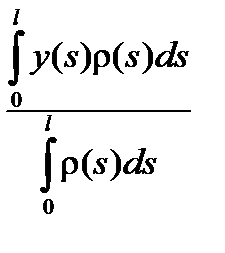 (2.14)
(2.14)
Если считать, что линейная плотность r(s)=1, то из второго равенства из (2.14) получим
2pYl =2p 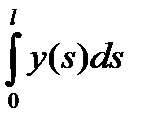 =S.
=S.
Последнее соотношение означает, что площадь поверхности, полученной вращением кривой вокруг оси c равномерно распределенной массой, равна длине этой кривой, умноженной на длину окружности, описанной центром тяжести этой кривой (первая теорема Гюльдена).
Пример. Пересчитать площадь поверхности тора по теореме Гюльдена.
Вторая теорема Гюльдена
Объем тела, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости этой фигуры и не пересекающей эту фигуру, равен произведению площади этой фигуры на длину окружности, описываемой центром тяжести этой фигуры.
Часть 3. Несобственные интегралы
3.1. Несобственный интеграл первого рода
Несобственные интегралы первого и второго рода. Критерий Коши сходимости несобственных интегралов. Признаки сходимости.
Теорема 2.
Если $ c > 0 $ p < 1 " x , xÎ[a , b) : 0 £ f(x)£ 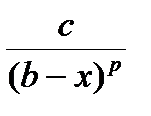 , то интеграл
, то интеграл 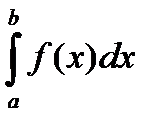 сходится.
сходится.
Если $ c > 0 $ p³ 1 " x , xÎ[a , b): f ( x)³ 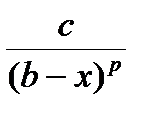 , то интеграл
, то интеграл  расходится.
расходится.
Утверждение следует из простого признака сравнения.
Теорема 3 ( Второй предельный признак сравнения). Если существует 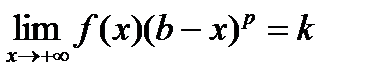 , (0 < k < +¥), то
, (0 < k < +¥), то
при p < 1 интеграл 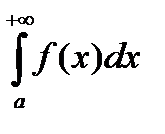 сходится,
сходится,
при p ³ 1 интеграл 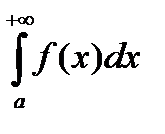 расходится.
расходится.
При k = 0 и p < 1 интеграл сходится,
при k = + ¥ , p ³ 1 интеграл расходится.
Утверждение теоремы следует из первого предельного признака сравнения.
Замечание. Аналогичные утверждения (Теоремы 1-3 и следствия имеют место для интегралов с особенностями в левом конце или во внутренней точке.
Пример 1. 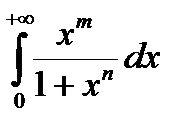 .
.
Пример 2. 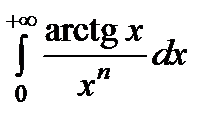
Пример 3. 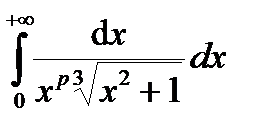
3.2. Абсолютная и условная сходимость несобственного интеграла. Признаки сравнения.
Абсолютная и условная сходимость. Интегрирование по частям, замена переменного. Формулы Эйлера.
Определение
Несобственный интеграл 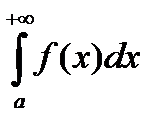 (или
(или  )называется абсолютно сходящимся, если сходится интеграл
)называется абсолютно сходящимся, если сходится интеграл  (или, для интеграла 2-го рода,
(или, для интеграла 2-го рода, 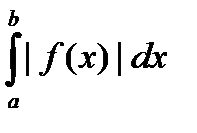 ).
).
Критерий Коши абсолютной сходимости. Для абсолютной сходимости интеграла первого рода 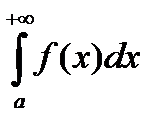 необходимо и достаточно выполнение условия
необходимо и достаточно выполнение условия
"e>0 $ M " R¢,R¢¢, M< R¢ < R¢¢ : 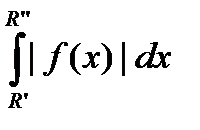 <e.
<e.
Для абсолютной сходимости интеграла второго рода 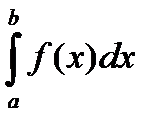 с особенностью в точке b необходимо и достаточно выполнение условия
с особенностью в точке b необходимо и достаточно выполнение условия
"e>0 $d "x¢, x¢¢, b - d < x¢ < x¢¢ < b: 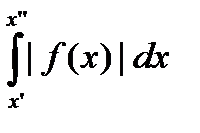 <e.
<e.
Замечание. Абсолютно сходящийся интеграл сходится.
Это следует из неравенства 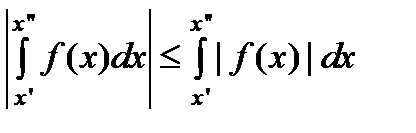 и критерия Коши.
и критерия Коши.
Обратное, вообще говоря, неверно.
Пример. 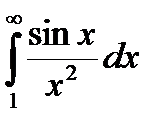 ,
, 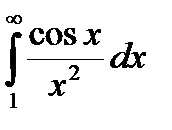 сходятся абсолютно, так как для подинтегральных функций справедливы неравенства
сходятся абсолютно, так как для подинтегральных функций справедливы неравенства  .
.
Пример. Интеграл 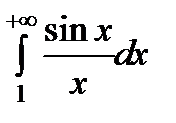 сходится. Действительно,
сходится. Действительно,
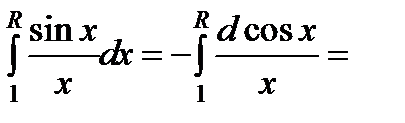
 .
.
Пример. Интеграл 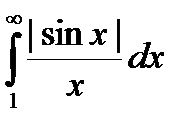 расходится.
расходится.
Действительно, для интеграла 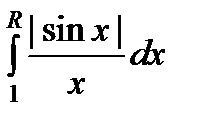 можно записать следующее неравенство
можно записать следующее неравенство
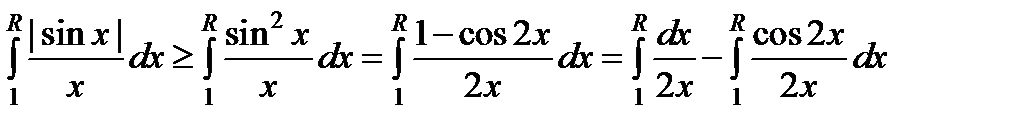 .
.
Так как интеграл 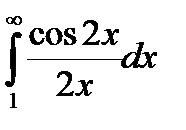 сходится, а второй интеграл
сходится, а второй интеграл 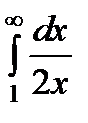 расходится, то и интеграл
расходится, то и интеграл 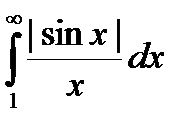 будет расходящимся.
будет расходящимся.
Определение. Несобственный интеграл 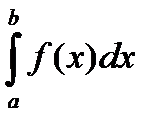 ( или
( или 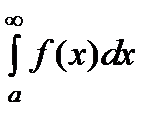 ) называются условно сходящимся, если
) называются условно сходящимся, если 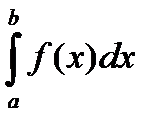 (или
(или 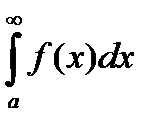 ) сходится, а интеграл
) сходится, а интеграл 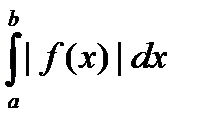 (или
(или 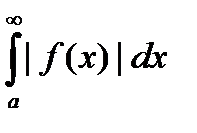 ) расходится.
) расходится.
Пример. Интеграл 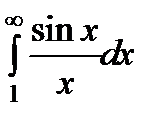 , как это следует из предыдущих примеров, сходится условно.
, как это следует из предыдущих примеров, сходится условно.
Теорема (Признак Абеля). Пусть f и g определены на [a ,+¥). f(x) интегрируема на [a ,+ ¥), g(x) монотонна и ограничена , тогда 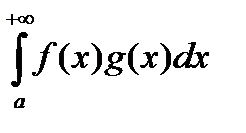 сходится .
сходится .
Доказательство. По третьей теореме о среднем (R ¢ < R ¢¢)
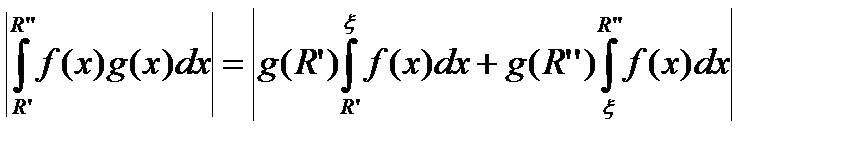 .
.
Правую часть в этом равенстве можно сделать сколь угодно малой выбором достаточно больших  .
.
Теорема (Признак Дирихле). Пусть f и g определены на [a ,+¥).
1) f(x) непрерывна и имеет ограниченную первообразную
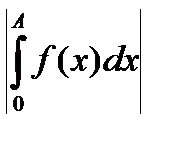 £ K , для " A³a ,
£ K , для " A³a ,
2) g(x) монотонна и стремится к 0 при x ® ¥ ,
тогда 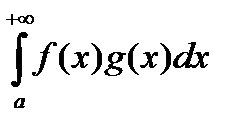 сходится.
сходится.
Доказательство. По третьей теореме о среднем (R ¢ < R ¢¢)
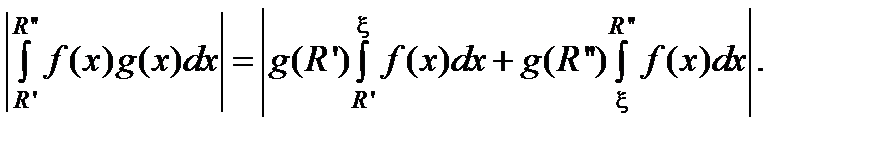
Правую часть в этом равенстве можно сделать сколь угодно малой выбором достаточно больших  .
.
.
Пример. 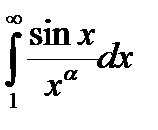 ,a>0, сходится по признаку Дирихле. Для этого в качестве функции
,a>0, сходится по признаку Дирихле. Для этого в качестве функции 
нужно взять sin x , а в качестве функции g(x) нужно выбрать функцию 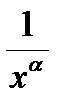 .
.
Формула замены переменного
Пусть f ( x ) непрерывна на [a , b) (b - число или символ +¥), j(t) – непрерывно-дифференцируема и строго монотонно возрастает на [a,b), a < b £ ¥, причем
a = j(a), 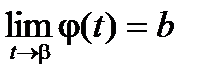 , тогда
, тогда
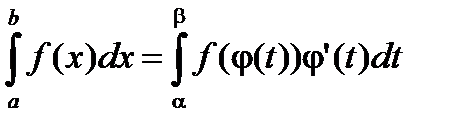 .
.
Доказательство. В силу строгой монотонности функции j(t) для "RÎ [a , b)$ r : j(r)= R .
Отметим, что при  будет и
будет и 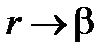 (слайд «Суперпозиция»).
(слайд «Суперпозиция»).
Суперпозиция
Далее следует перейти к пределу в равенстве
 , (r®b, R ® b).
, (r®b, R ® b).
Замечание 1. В формуле замены переменной функция j может быть строго монотонно убывающей. Тогда в формулировке теоремы появятся соответствующие изменения j(b)= a , 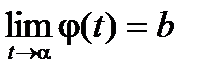 ,
, 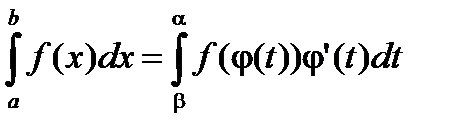 (рис. 3.4).
(рис. 3.4).

Рис. 3.4
Замечание 2. Формула замены переменного справедлива и без условия монотонности функции j.
Например, пусть функция j имеет три интервала монотонности (см. рис. 3.5)

Рис. 3.5
Тогда
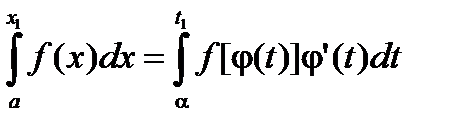 ,
, 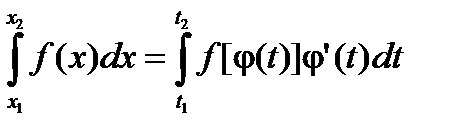 ,
, 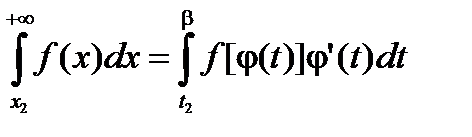 .
.
Складывая эти равенства, получим ту же формулу замены переменного и для данного случая
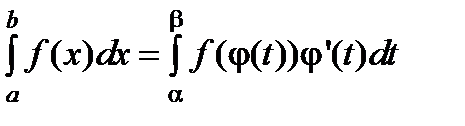 .
.
Замечание 3. Несобственный интеграл 1-го рода может быть подходящей заменой сведен к несобственному интегралу 2-го рода и наоборот.
Пример 1. 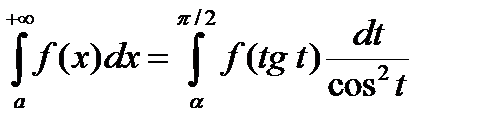 .
.
При некоторых заменах переменной вновь полученный интеграл может оказаться собственным (см. пример 2).
Пример 2. 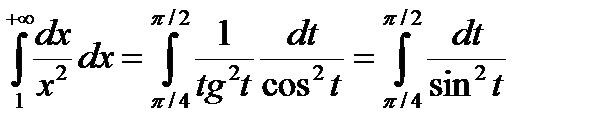
|  Рис. 3.6
Рис. 3.6
|
Функции Эйлера
Гамма- функция Эйлера G(p)=  , определена при p > 0 .
, определена при p > 0 .
Для доказательства сходимости интеграла в области p > 0 отметим, что в окрестности 0 подинтегральная функция эквивалентна функции 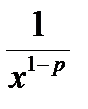 , интеграл от которой сходится при условии 1- p < 1, то есть p > 0. В окрестности +¥ , подинтегральную функцию можно сравнивать с функцией
, интеграл от которой сходится при условии 1- p < 1, то есть p > 0. В окрестности +¥ , подинтегральную функцию можно сравнивать с функцией  (имеющей сходящийся интеграл), именно,
(имеющей сходящийся интеграл), именно, 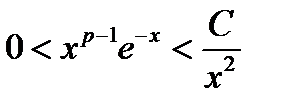 или
или 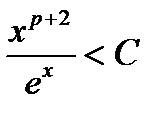 . Существование константы C, для которой эти неравенства будут выполнены, следует из соотношений
. Существование константы C, для которой эти неравенства будут выполнены, следует из соотношений
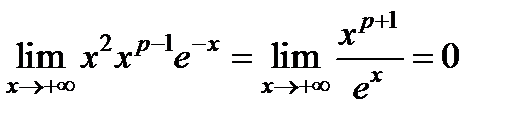 , при p > 0.
, при p > 0.
Далее можно воспользоваться простейшим признаком сравнения.
Легко проверить, что G(1) = 1 (вычислить интеграл), G(p+1) = pG(p). Последнее равенство следует из формулы интегрирования по частям
G(p)= 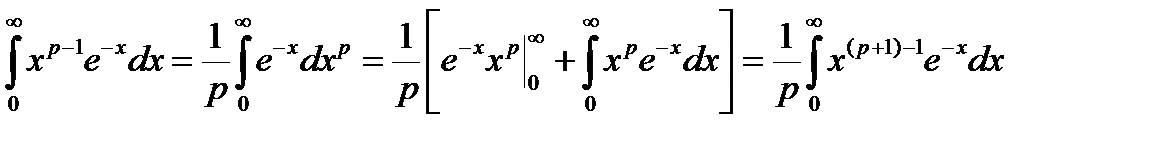 =
= 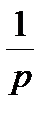 G(p +1).
G(p +1).
Бета-функция Эйлера определяется по формуле
B(p , q)= 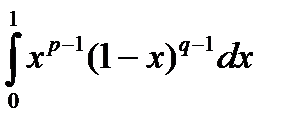 ,определена для p > 0, q > 0 .
,определена для p > 0, q > 0 .
Часть 4. n – мерное евклидово пространство
4.1. Основные определения
Метрические пространства, норма, скалярное произведение. Неравенство Коши-Буняковского. Сходимость.
Метрика. Расстояние
Рассмотрим всевозможные упорядоченные наборы из n - вещественных чисел
x = (x1, x 2 ,…, xn).
Пользуясь геометрической терминологией, x будем называть точкой, числа x1, x2,…, xn называются координатами точки. Для случаев n =1,2,3 мы имеем дело с точками на прямой, плоскости и в пространстве, соответственно. Для двух точек x = (x1, x2,…, xn), y = (y1, y2,…, yn) величина
r(x , y)= 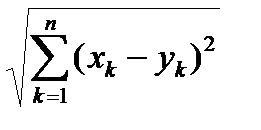
называется расстоянием между этими точками. Фундаментальными свойствами расстояния являются следующие три свойства.
1) " x,y :r(x,y) ³ 0, r(x,y) = 0 Û x = y
2) " x,y :r(x,y) = r(y,x)
3) " x , y , z :r(x , y) £ r(x , z) + r(z , y) (неравенство треугольника)
Первые два свойства очевидны, третье свойство будет доказано позже. Множество всевозможных точек x с расстоянием r(x , y), удовлетворяющим свойствам 1)-3) называется метрическим пространством. Обозначим это пространство Rn .
Предел функции
Определение. Пусть D – некоторое множество точек пространства Rn . Если для "x Î D по некоторому закону сопоставлено единственное число u Î R , то говорят, что задана функция, определенная на множестве D . При этом пишут
u = f(x)= f(x1, x2,…, xn),
D называется областью определения функции f .
Функция осуществляет отображение множества D на некоторое множества из R1.
В случае функции двух переменных z= f(x , y) , определенной на множестве D , можно ввести понятие графика функции. Графиком называют геометрическое место точек (x , y , f(x , y)), (x , y) Î D . Геометрически, график функции может представлять собой некоторую поверхность (рис. 4.6).
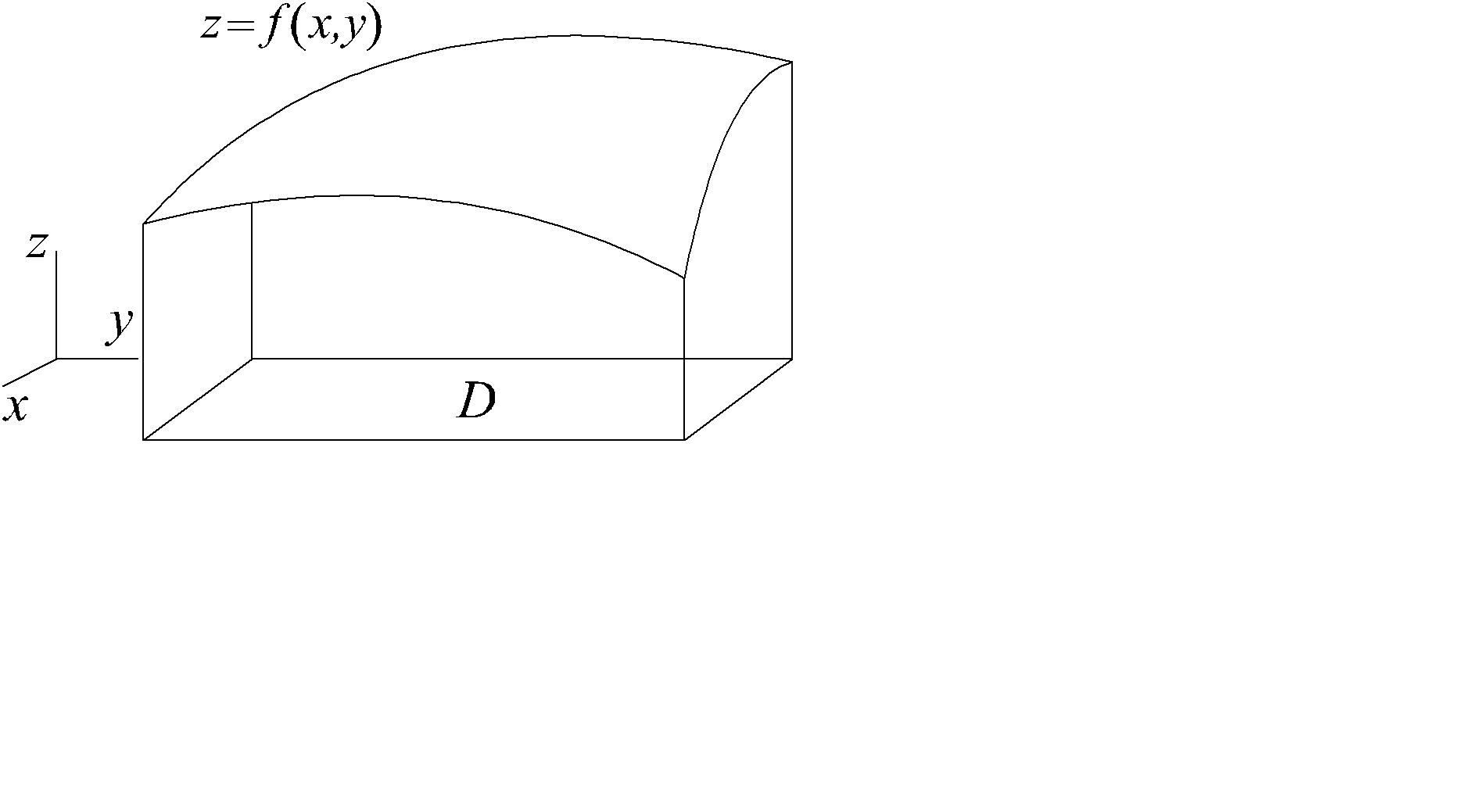
Рис. 4.6
Для исследования поверхности бывает удобно пользоваться линиями уровня. Для заданной поверхности линией уровня z = z0 называется “кривая”, заданная уравнением z0= f(x , y).
Определение. Пусть f определена на D Ì Rn , и x0 – предельная точка множества D . Число A называется пределом функции f при x ® x0 , если
"e>0$d>0"xÎDÇ 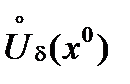 :| f(x) - A|<e.
:| f(x) - A|<e.
Пишут 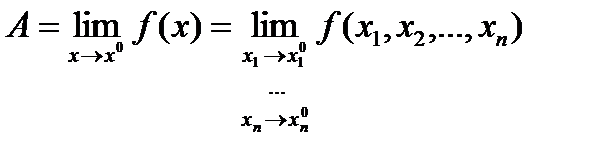 .
.
Если предел существует, то он единственен.
Аналогично тому, как это делалось для функции одного переменного, определяются пределы с участием символов ¥. Окрестностью ¥ называется множество Ur(¥)={x Î Rn:r(x ,q)>r}, 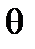 - начало координат.
- начало координат.
 ,
, 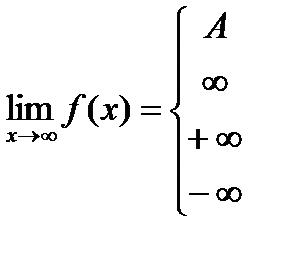
Примеры.  ;"N$d>0"xÎD ,0<r(x , x0)<d:| f(x)|> N .
;"N$d>0"xÎD ,0<r(x , x0)<d:| f(x)|> N .
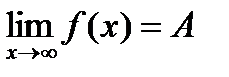 ;"e>0$r"xÎD ,r(x ,q)>r:|f(x)- A|<e, q=(0,0,…,0).
;"e>0$r"xÎD ,r(x ,q)>r:|f(x)- A|<e, q=(0,0,…,0).
Определение предела по Гейне. 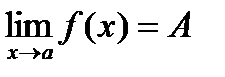 . Для любой последовательности типа Гейне {xk} выполнено
. Для любой последовательности типа Гейне {xk} выполнено 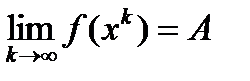 .
.
В этом определении a может быть точкой или символом ¥ , A –может быть числом или символами ¥ , + ¥ , - ¥ . Последовательность типа Гейне определяется, как последовательность, удовлетворяющая условиям:
1) xkÎ D , 2) xk ¹ a , 3) 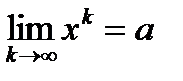 .
.
Можно показать, что определение по Гейне и по Коши эквивалентны.
Свойства пределов
Для пределов функций многих переменных имеют место те же свойства, что и для функции одного переменного: локальная ограниченность функции, имеющей конечный предел, сохранение знака функции, имеющей не нулевой предел, свойства арифметических операций ( сложение, умножение, деление). Докажем, например, свойство для произведения пределов.
Если существуют конечные пределы 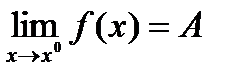 ,
, 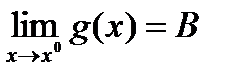 , то будет существовать
, то будет существовать 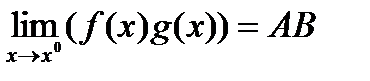 .
.
Доказательство проводится, используя определение предела по Гейне. Пусть {xk} последовательность типа Гейне (xk ® x0 ) . Тогда 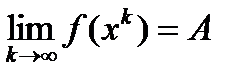 ,
,  . Откуда следует, что
. Откуда следует, что 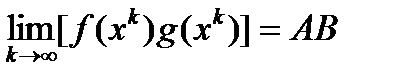 , поэтому
, поэтому  .
.
Регулярные отображения
Определение. Отображение f называется регулярным, если оно взаимно однозначно и оба отображения f , f –1 Î C1 .
Теорема (о локальной обратимости непрерывно дифференцируемого отображения). Пусть задано отображение
 ,
,
определенное на D и x0 = 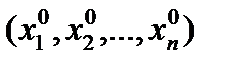 Î D внутренняя точка D . Если f Î C1 в окрестности точки x 0 и
Î D внутренняя точка D . Если f Î C1 в окрестности точки x 0 и  ¹ 0 в точке x 0 , то существуют открытые множества U , V , x0Î U , y0Î V , y0= f(x0) такие, что f взаимно однозначно отображает U на, V . При этом отображение f -1 непрерывно дифференцируемо.
¹ 0 в точке x 0 , то существуют открытые множества U , V , x0Î U , y0Î V , y0= f(x0) такие, что f взаимно однозначно отображает U на, V . При этом отображение f -1 непрерывно дифференцируемо.
Необходимые условия
Рассмотрим функцию
u = f(x1, x2,…., xn , xn +1,…, xn + m), или кратко u = f(x) (6.12)
определенную в области D Ì Rn + m . Обозначим через D1 множество точек из D , удовлетворяющих n условиям
 , Ф(x)=0. (6.13)
, Ф(x)=0. (6.13)
Условия (6.13) назовем уравнениями связи.
Определение. Точка x0=( 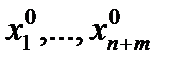 ) называется точкой условного максимума функции (6.12) при связях (6.13), если существует окрестность этой точки U(x0) такая, что
) называется точкой условного максимума функции (6.12) при связях (6.13), если существует окрестность этой точки U(x0) такая, что
"xÎU(x0)ÇD1 : f(x)< f(x0).
Аналогично определяется условный минимум и условный экстремум.
Введем обозначения p =(x1, x2,…, xn), q =(xn +1, xn +2,…, xn + m), x =( p , q)=(x1, x2,…, xn + m), p0=( 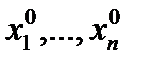 ), q0=
), q0= 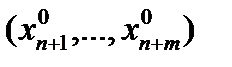 , x0=(, p0 ,q0)=(
, x0=(, p0 ,q0)=(  ). Будем предпологать, что ФÎ C1(U(x0)) и
). Будем предпологать, что ФÎ C1(U(x0)) и
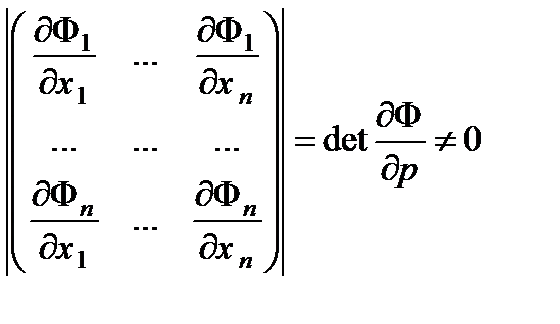 , в точке x0.
, в точке x0.
Можно считать, что якобиан отличен от нуля в U(x0 ). В этом случае в каждой точке этой окрестности выполнены условия теоремы существования и единственности системы функций, заданных неявно системой уравнений (6.13) и эту систему можно разрешить относительно p в окрестности точки q 0 = 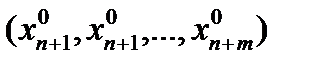
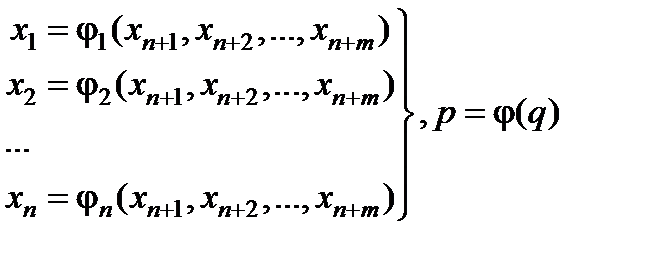 (6.14)
(6.14)
Таким образом, любая точка из области U(x0)ÇD1 может быть записана в виде
(j1(q),j2(q),…,jn(q), q).
Тогда необходимым и достаточным условием для условного экстремума в точке x0 будет «безусловный» экстремумом функции
F(q) = f(j1(q),j2(q),…,jn(q), q) в точке q0.
В силу этого необходимыми условиями условного экстремума будет условия
 j = n +1, n +2,…, n + m .
j = n +1, n +2,…, n + m .
В частности,
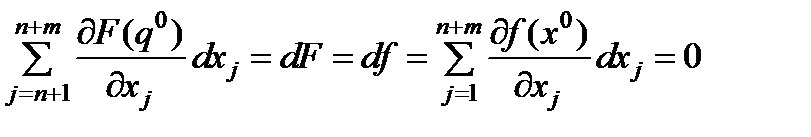 (6.15)
(6.15)
Продифференцируем тождества (6.13)
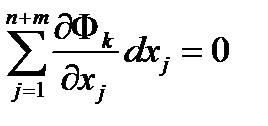 (6.16k)
(6.16k)
Умножим каждое уравнение (6.16k) на l k сложим их c уравнением (6.15). В результате получим
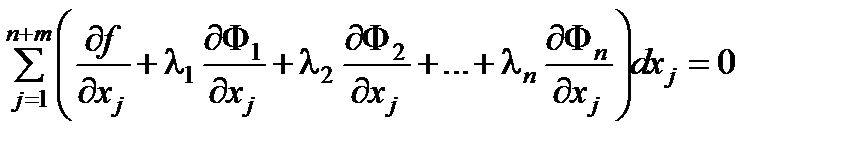 (6.17)
(6.17)
Выберем li так, чтобы множители при зависимых дифференциалах dxj (т.е. при j =1,2,…,n) обращались в 0
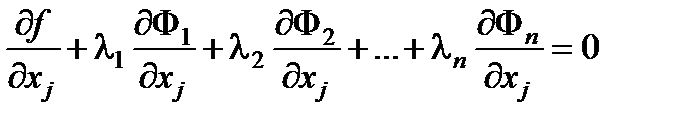 , j =1,2,…, n . (6.18)
, j =1,2,…, n . (6.18)
Это можно сделать в силу того, что 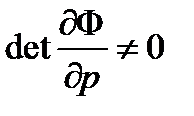 . Тогда из (6.17) получим
. Тогда из (6.17) получим
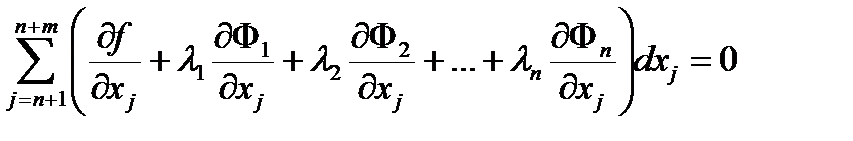 . (6.19)
. (6.19)
Так как dxj , j = n +1,…, n + m – дифференциалы независимых переменных, то из (6.19) следует, что все множители при этих дифференциалах равны нулю
 , j = n +1, n +2,…, n + m . (6.20)
, j = n +1, n +2,…, n + m . (6.20)
Таким образом, как это следует из (6.18), (6.20) для всех j будут выполнены равенства
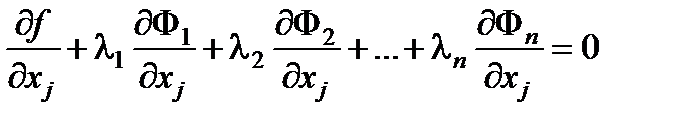 , j =1,2,…, n + m . (6.21)
, j =1,2,…, n + m . (6.21)
Поводя итог, можно сказать, что точка условного экстремума x0 должна удовлетворять системам уравнений (6.13), (6.21)
 ,
,
 , j =1,2,…,n + m ,
, j =1,2,…,n + m ,
которые дают m +2n уравнений для определения m +2n неизвестных. Этими неизвестными являются: n + m координат точки x0 и n неопределенных множителей lj . Эти множители называются множителями Лагранжа. Доказанное утверждение сформулируем в виде теоремы
Теорема (необходимые условия для условного экстремума). Пусть функция
u = f(x1,…, xn + m)
определена в области D Ì Rn + m , x0 внутренняя точка D и заданы n непрерывно дифференцируемые связи
 ,
,
причем
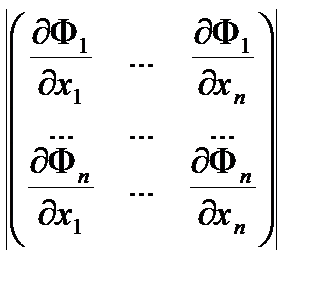 ¹0, в точке x0.
¹0, в точке x0.
Тогда в точке x0 выполнены условия
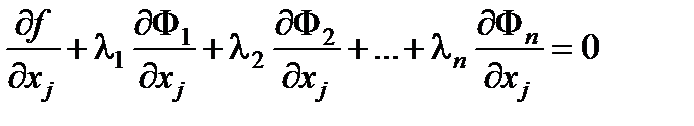 , j =1,…, n + m . (6.22)
, j =1,…, n + m . (6.22)
Замечание. При составлении уравнений (6.22) для поиска точек «подозрительных» на условный экстремум удобно использовать функцию Лагранжа
L = f + 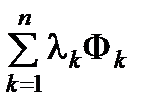 ,
,
условия (6.22) тогда запишутся в виде
 (или dL=0).
(или dL=0).
Достаточные условия
Пусть в точке x0= 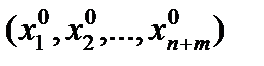 выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df = f(x) – f(x0) при условии, что xÎD1 (область, определяемая уравнениями связи). Для таких точек DFi = 0, поэтому Df = DL , и исследование поведения Df сводится к исследованию поведения приращения функции Лагранжа DL . По формуле Тейлора
выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df = f(x) – f(x0) при условии, что xÎD1 (область, определяемая уравнениями связи). Для таких точек DFi = 0, поэтому Df = DL , и исследование поведения Df сводится к исследованию поведения приращения функции Лагранжа DL . По формуле Тейлора
DL = 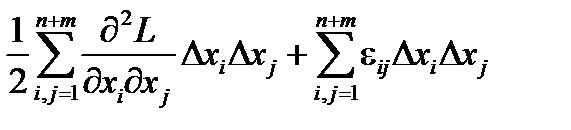 , eij ® 0 при Dxi ® 0.
, eij ® 0 при Dxi ® 0.
Если выразить приращения Dxi (i =1,…. n ) зависимых переменных через приращения Dxk (k = n +1,…. n + m) независимых переменных (это можно сделать, продифференцировав уравнения связи), то можно получить выражение для DL следующего вида
DL = 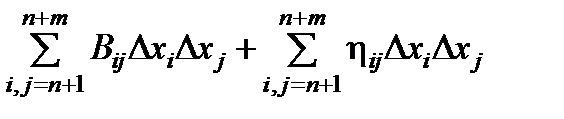 , hij ®0 при Dxi ®0.
, hij ®0 при Dxi ®0.
После этого можно использовать достаточные условия, выведенные для «безусловных» экстремумов по квадратичной форме 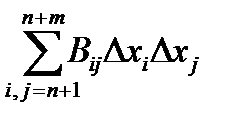 .
.
Пример 1. Частный случай
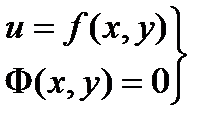 , L = f +lF, dL =0 (необходимое условие)
, L = f +lF, dL =0 (необходимое условие)
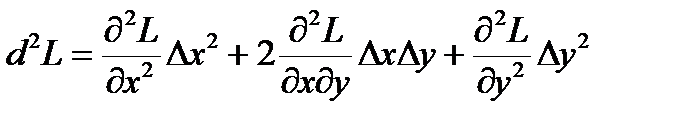 , DL =
, DL = 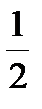 d 2 L +er2,
d 2 L +er2,
0= dF= 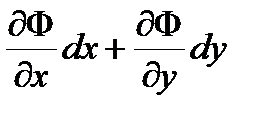 , dy =–
, dy =– 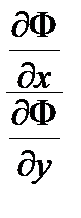 dx , после подстановки получим
dx , после подстановки получим
DL = BDx2+ o(Dx2). В зависимости от полученного коэффициента B можно сделать вывод о наличии условного экстремума.
Пример 2.
u = x2+12xy +2y2, 4x2+ y2=25.
L=x2+12xy+2y2+l(4x2+y2–25), dL=(2x+12y+8lx)dx+(4y+12x+2ly)dy,
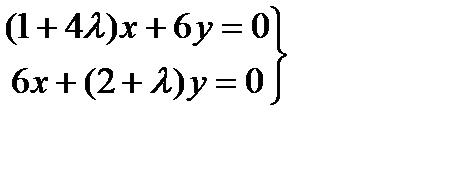 ,
,  , 4l2+9l-34=0, l1,2=2;
, 4l2+9l-34=0, l1,2=2; 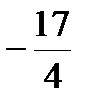 .
.
l1=2, 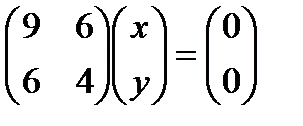 ,3x +2y =0, y =-
,3x +2y =0, y =- 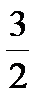 x ,
x ,
4x2+ 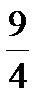 x2=25,
x2=25, 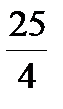 x2=25, x =±2,
x2=25, x =±2,
l1=2, точки (2,-3), (-2,3).
l2= 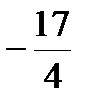 ,
,  ,-8x +3y =0, y =
,-8x +3y =0, y = 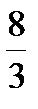 x , 4x2+
x , 4x2+  x2=25,
x2=25, 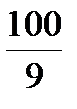 x 2=25, x = ±
x 2=25, x = ± 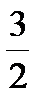 .
.
l1= 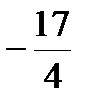 , точки (
, точки ( 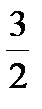 ,4), (-
,4), (- 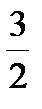 ,-4).
,-4).
d2L=(2+8l)dx2+24dxdy +(4+2l)dy2, 8xdx +2ydy =0, dy = -4 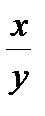 dx .
dx .
1) (2,-3), l=2
d2L =(2+16)dx2-24·4 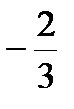 dx2+8·16
dx2+8·16  dx2=[18+64+…]dx2 минимум.
dx2=[18+64+…]dx2 минимум.
Пример 3 (3659). u = x – 2y + 2z , x2 + y2 + z2 = 1
L = x – 2y + 2z +l( x2 + y2 + z2 – 1)
dL =(1 + 2l x)dx +( – 2 + 2l y)dy +(2 + 2l z)dz,
d 2L = 2l dx2 + 2l dy2 + 2l dz2
1 + 2lx = 0, -1 + l y = 0, 1 + l z =0,
x =  , y =
, y = 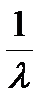 , z =
, z = 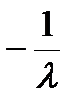 , подставляя в уравнение связи найдем l = ±3/2
, подставляя в уравнение связи найдем l = ±3/2
(-1/3, 2/3, -2/3), l = 3/2
(1/3, -2/3, 2/3) l = -3/2, дифференцируя уравнение связи получим
xdx + ydy + zdz = 0, dz = 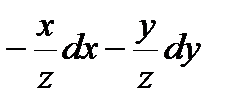 , dz2 = …,
, dz2 = …,
d 2L = … = 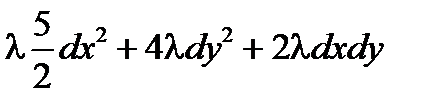 главные миноры
главные миноры 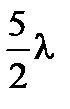 , 9l2.
, 9l2.
Интегральное исчисление и функции многих переменных
Дата: 2019-03-05, просмотров: 327.