Якщо змінні визначаються через нечіткі канали спостереження, то кожне спостереження записується як впорядкована пара, що складається із значення повного параметра, з яким пов'язано спостереження, і вектора 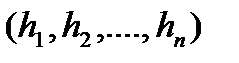функцій

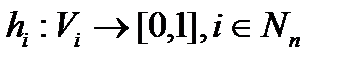(3.10)

де виражає ступінь упевненості в тому, чтоявляєтся наблюденним станом змінної .

Формалізуємо поняття нечітких даних. Хай

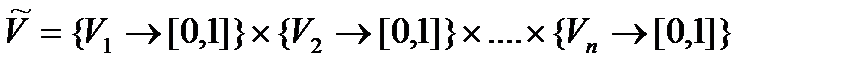.(3.11)

Тоді нечіткі дані представляються функцією

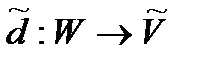. (3.12)

Для будь-якого значення повного параметра

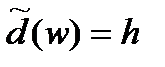(3.13)

де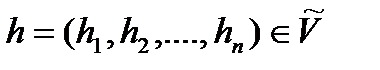

Представлення даних

_ З яким типом даних - чітким або нечітким - ми маємо справу, завжди ясно по контексту. Чіткі дані можуть бути представлені в самому різному вигляді. Хай стандартною формою представлення дискретних змінних і параметрів буде матриця

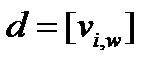(3.14)

елементами якої є стани змінних, наблюденниє при відповідних значеннях повного параметра w (мал. 3.1,а). Кожен стовпець матриці d задає повний стан, наблюденноє при даному w, а кожен рядок - всі спостереження однієї змінної на параметричній безлічі W. Якщо W лінійно впорядковане, то і стовпці в матриці d повинні бути впорядковані таким самим чином. Якщо використовуються декілька параметрів, то може опинитися зручніше використовувати інші форми уявлення.

Для нечітких даних стандартною формою уявлення, подібній матриці, є тривимірний масив 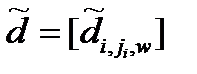(3.15)

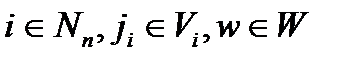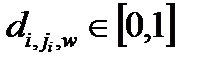елементами якого є значення ступеня упевненості в тому, що при заданому значенні параметра w спостерігався стан змінної , а . Масив є набором матриць (мал. 3.1,б), по одній для кожної змінної. Стовпець в матриці змінної задає функцію, визначувану рівнянням (3.10).

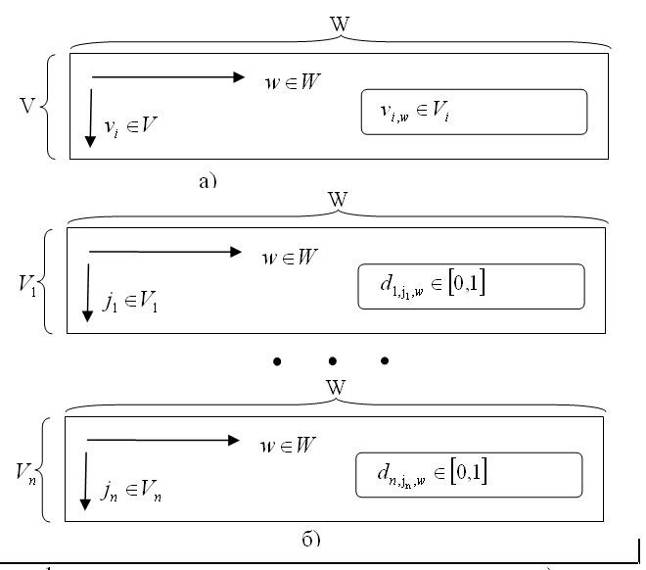
Рис. 3.1. Стандартне представлення данних для дискретних змінних. А) Чіткі дані. Б) Нечіткі дані.

К.Р. № 8

Опишіть формально деяку систему даних з нечіткими каналами спостереження.

Приведіть приклад представлення даних.

Алгоритм формалізації систем даних

1.Визначається функція 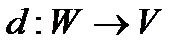, де ,  .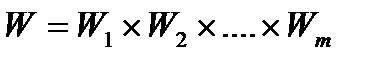

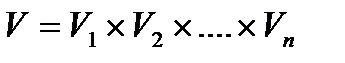2.Визначається система даних 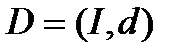.Система даних з семантикою 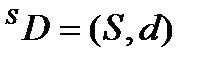. Направлені аналоги , .

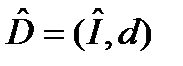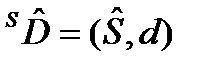Для систем даних з нечіткими каналами спостереження

1. Визначаються функції 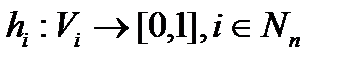, де 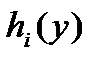 виражає ступінь упевненості в тому, чтоявляєтся наблюденним станом змінної  .

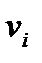2.Нечіткі дані представляються функцією 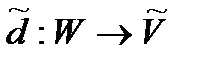, де .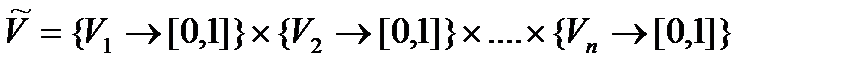

Лекція 9

4. Породжуючі системи

Системи з поведінкою

Термін поведінка використовується для характеристики загального параметрично інваріантного обмеження на змінні узагальненої представляючої системи і, можливо, на деякі додаткові абстрактні змінні. Додаткові змінні визначаються на параметричній множині за допомогою правил зрушення.

Оскільки опис параметрично інваріантного обмеження на дані змінні може бути використано для породження станів змінних при даній параметричній множині, системи, такі обмеження, що містять, називаються системами, що породжують. Поведінка є однією з форм завдання цього обмеження.

Для заданої узагальненої представляючої системи діапазон можливих типів параметрично інваріантних обмежень залежить від властивостей, що приписуються параметричній множині. Якщо на цій безлічі ніяких властивостей не визначено (як це часто буває для груп), то стани змінних можуть обмежувати тільки один одного. Проте якщо параметрична множина впорядкована, стани змінних можуть обмежуватися не тільки іншими станами, але і станами вибраного сусідства для кожного конкретного значення параметра.

Сусідство на впорядкованій параметричній множині звичайно називається маскою і визначається через змінні, параметричну множину і набір правил зрушення на параметричній множині. Правило зрушення, скажемо правило,- це однозначна функція

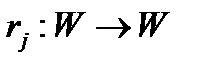 (4.1)

яка кожному елементу W ставить у відповідність інший (причому єдиний) елемент W. Якщо, наприклад, параметрична множина повністю впорядкована (як у випадках, коли розглядається час або одночасний простір) і є безліччю послідовних цілих позитивних чисел, то будь-яке правило зрушення може бути задано простим рівнянням

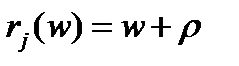 (4.2)

де - ціла константа (позитивна, негативна або нуль). При називається тотожним правилом зрушення.

Все вище сказане, можна пояснити таким чином. Для того, щоб система, була здатна генерувати дані, з початкових даних, потрібно визначити деякі правила по яких виходитимуть нові дані. У вузькому сенсі це будуть деякі функції. Наприклад, лінійна функція однієї змінної - геометрично пряма. Ця функція перетворить значення аргументу, в деяке значення. У ширшому сенсі це параметрично інваріантне обмеження.

Вибіркові змінні і маски

Хай задана узагальнена представляюча система I, визначувана рівнянням (2.12). Позначимо через V безліч змінних з I, а через R набір правил зрушення, що розглядаються для цих змінних. Тоді безліч змінних

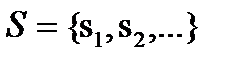(4.3)

званих вибірковими змінними, може бути введено за допомогою рівнянь

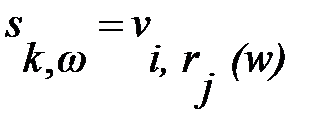(4.4)

для деяких змінних і правил зрушення ; позначає стан вибіркової змінної при значенні параметра w, а - стан змінної при значенні параметра, тобто при значенні, одержаному для заданого w, при застосуванні правила зрушення . Для повністю впорядкованої параметричної множини, правила зрушення якого мають вигляд (4.2), рівняння (4.4) може бути переписано в певнішому вигляді

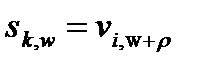(4.5)

Оскільки будь-яке правило зрушення з набору R може бути застосовано до будь-якої змінної з множини V, та безліч всіх можливих вибіркових змінних представляється декартовим твором . Насправді розглядаються вибіркові змінні, що характеризуються відношенням

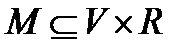 (4.6)

так, що всякій парі відповідає одне рівняння з (4.4). Відношення М представляє схему сусідства на параметричній множині, в термінах якої визначені вибіркові змінні. Ця схема звичайно називається маскою.

Для введення ідентифікаторів вибіркових змінних до повинна бути введена якась однозначна функція (кодування).

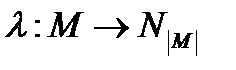 (4.7)

де - це кількість елементів множини М.

Якщо вибіркова змінна визначена через змінну і деяке правило зрушення згідно рівнянню (4.4), то безліч станів, очевидно, То ж саме, що і безліч станів тобто . Проте для зручності позначень безліч станів вибіркової змінної позначатимемо ; сенс будь-якого 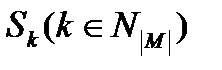 однозначно визначається маскою в термінах однієї з множин 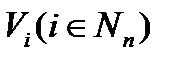. Таким чином, декартовий твір 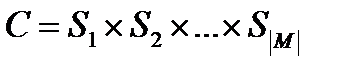(4.8)

є повною безліччю станів вибіркових змінних.