Для заданої системи даних D і найбільшої допустимої маски М вимога відповідності приводить до обмеженої множини

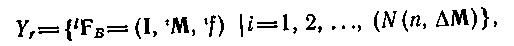 (4.58)

що містить по одній системі з поведінкою для кожної осмисленої маски ; хай для зручності . Наступним кроком рішення даної задачі повинне бути обчислення ступенів недетермінованої і складності для всіх систем з множини.

Як було показано ступінь недетермінованої задається відповідною мірою нечіткості, що породжує, визначуваною для імовірнісних систем шенноновськой ентропією.

Що стосується міри складності, то тут можливо багато варіантів. Візьмемо для прикладу просту, але змістовну міру, яку часто використовують в АСНД - розмір (потужність) маски.

Хай - значення тих, що відповідних породжують нечеткостей для систем з поведінкою з обмеженої множини Оскільки будь-яка система однозначно ідентифікується своєю маскою М, потужність якої задає її складність, статус системи в сенсі нечіткості, що породжує, і складності зручно описувати парою .

Чисельне впорядкування масок, що ідентифікують системи з по їх потужності, задає впорядкування складності на множині . Чисельне впорядкування значень визначає впорядкування по нечіткості на безлічі Yr. В той час, як впорядкування по складності повністю визначається самими масками, впорядкування по нечіткості може бути визначено тільки після оцінки масок. Для будь-якої безлічі масок, що породжують, ми можемо визначити часткове впорядкування тоді і тільки тоді, коли

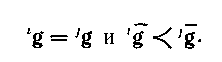 (4.59)

(ілідля направлених систем), яке ми називатимемо впорядкуванням підмасок.

Приклад впорядкованості по складності і впорядкованості підмасок для найбільшої допустимої маски М при n=3 і приведений на мал. 3.10. При цьому передбачається, що дані породжуються зліва направо. Всі змістовні підмаски зображаються своїми матрицями і помічені в лівому верхньому кутку своїми ідентифікаторами i. По складності вони розбиті на чотири групи. Маски з однаковою складністю розташовані на одному рівні. Наприклад, маски з ідентифікаторами 2-7 утворюють групу з складністю 5, маски 8-19 - іншу групу з складністю 4 і т.д. З погляду впорядкованості по складності будь-яка маска деякого рівня є безпосереднім наступником будь-якої маски найближчого вищого рівня і безпосереднім попередником будь-якої маски найближчого нижчого рівня. На мал. 4.7 стрілками показано впорядкування по підмасках. З цього прикладу видно, що впорядкування по складності - це зв'язне квазівпорядкування (і транзитивної відношення, рефлексії, визначене для будь-якої пари систем).

Впорядкування по підмасках - це часткове впорядкування, але грати воно не утворює. Проте воно є набором грат по одній для кожної безлічі породжуваних вибіркових змінних (у нашому прикладі це крайні праві елементи масок).

Впорядкування по нечіткості зв'язне, але через те, що декілька різних систем можуть мати ту, що однакову породжує нечіткість, це відношення не є антисиметричним. Отже, в загальному випадку це зв'язне квазівпорядкування, яке в деяких окремих випадках опиняється повним впорядкуванням.

Таким чином, на множині визначені два зв'язкових квазівпорядкування - по складності і по нечіткості. Оскільки для даного типа завдань потрібний, щоб і складність, і що породжує нечіткість систем в безлічі рішень YQ була мінімізована, відповідне об'єднане впорядкування визначається таким чином: тоді і тільки тоді, коли

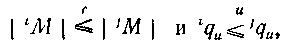 (4.60)

де. Це впорядкування не є зв'язковим, оскільки пари, для яких іїлі (подібні пари, зрозуміло, можуть існувати), незрівняні. Воно також неантисиметрично, оскільки не виключена можливість того, що

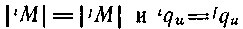(4.6ё)

для деяких . Отже, об'єднане впорядкування - це загального вигляду квазівпорядкування (і транзитивної відношення, рефлексії) на .

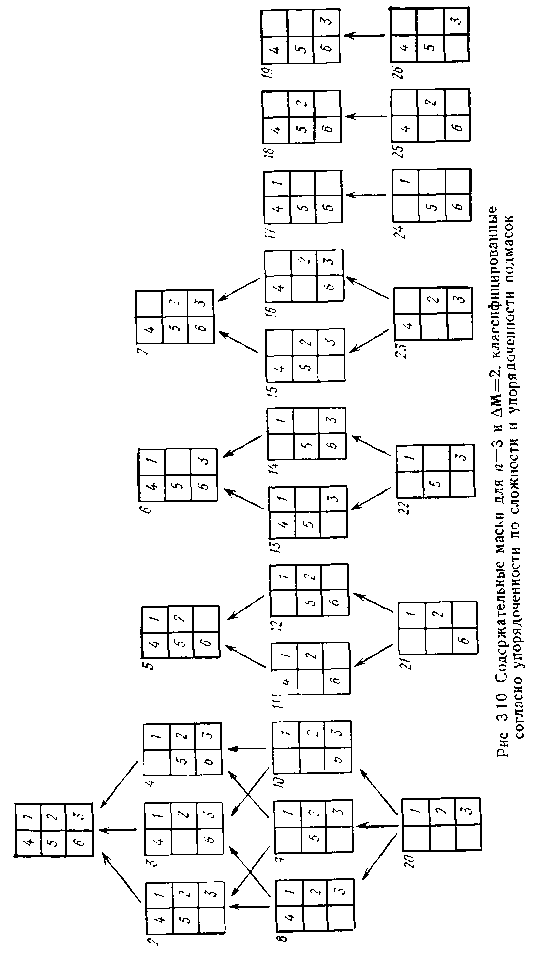
Мал. 4.7 Змістовні маски для класифіковані згідно впорядкованості по складності підмасок

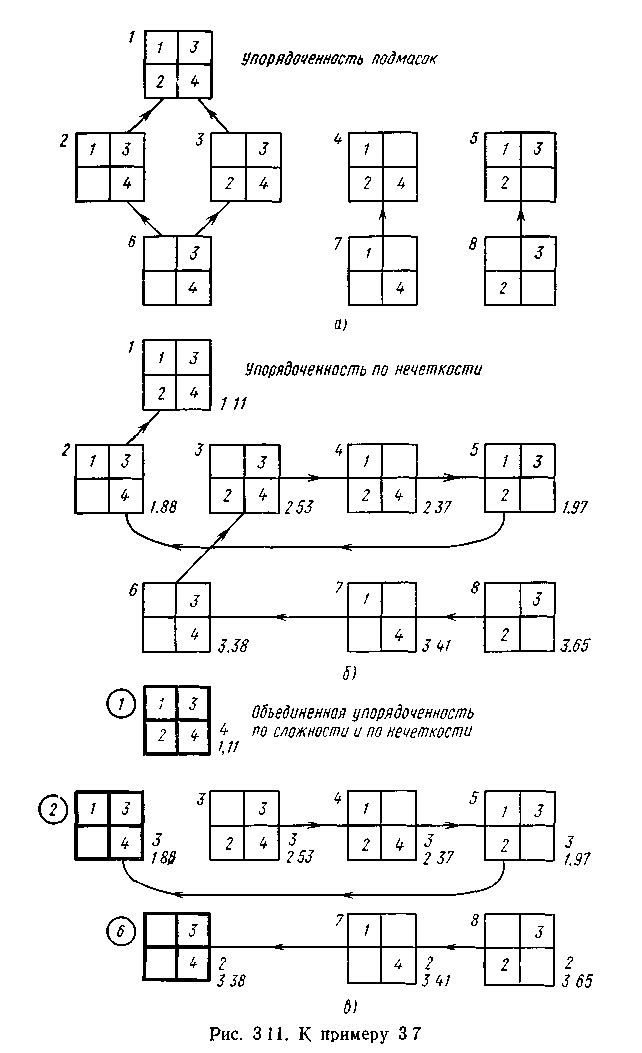
Мал. 4.8

Тепер безліч рішень можна визначити як безліч всіх систем з, які або еквівалентні, або незрівняні щодо об'єднаного впорядкування (4.60). Дві системи з, скажемо системи і, незрівняні в сенсі об'єднаного впорядкування, якщо виконано одну з наступних умов:

(а) складніша і більш детермінована, чим або менш складна і менш детермінована, чим. Формально

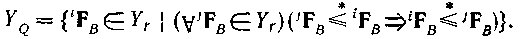 (4.62)

Системи з безлічі рішень називатимемо відповідними системами з поведінкою для даного типа завдань.

Приклад 4.4. Щоб пояснити різні питання, що вивчаються в даному розділі, розглянемо деяку систему даних. Визначимо всі відповідні в сенсі (4.62) системи з поведінкою для цієї системи даних в припущенні, що необхідно одержати опису імовірнісних систем з поведінкою і використовувати їх для прогнозу.

Припустимо спочатку, що . Тоді є вісім змістовних масок, які разом з їх впорядкуванням підмасок і вказівкою трьох рівнів складності зображені на мал. 4.8,а. Після виконання вичерпної вибірки для найбільшої прийнятної маски по певній формулі, по частотах N(c) обчислюється вірогідність, а нечіткість, що породжує, обчислюється або за формулою (4.48). Якщо для обчислення вірогідності використовується формула (4.31), то нечіткість, що породжує, рівна 1.11. Потім для решти семи змістовних масок по формулі (4.57) визначаються відповідні проекції і обчислюються їх породжують нечіткості. Результати цих обчислень показані на мал. 4.8,б (у правому нижньому кутку масок). На мал. 4.8,б також зображено впорядкування масок по нечіткості. В даному прикладі впорядкування є повним, оскільки значення нечіткості у всіх різні. Об'єднане впорядкування по складності і нечіткості (3.60) зображене на мал. 4.8,в. Як ми бачимо, мінімальними з погляду об'єднаного впорядкування є маски

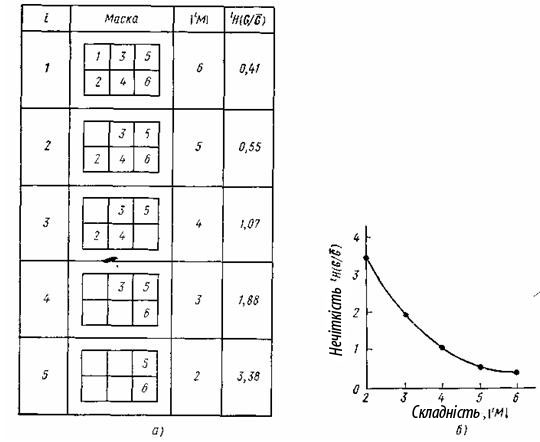
Мал. 4.9 Відповідні системи з поведінкою з прикладу 4.4

з ідентифікаторами 1, 2, 6. Отже 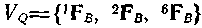. Припустимо тепер, що =3. Тоді згідно формулі (4.36) є 40 змістовних масок. Після їх обробки, аналогічній обробці для випадку, ми одержимо п'ять відповідних систем з поведінкою, маски яких, значення складності і що породжують нечіткості приведені на мал. 4.9,а. 35 масок, що Залишилися, гірше з погляду їх складності, як і з погляду чіткості, і, отже, їх зовсім не потрібно розглядати. Мал. 4.9,а - це типовий приклад відповіді АСНД. При відповідних запитах можуть також видаватися різні додаткові характеристики, безліч рішень, такі, як графік залежності нечіткості від складності, зображений на мал. 4.9,б.

Описаний тут пошук відповідних систем з поведінкою може бути реалізований самими різними способами. Основний принцип полягає в тому, що змістовні маски виходять за допомогою деякого алгоритму з найбільшої прийнятної маски у порядку складності, що зменшується. Серед масок однакової складності вибираються тільки маски з мінімальною нечіткістю, що породжує. При цьому якщо значення цієї мінімальної нечіткості менше або рівно значенню нечіткості для попереднього рівня складності, то всі раніше прийняті системи відкидаються. В результаті застосування цієї процедури у нас залишаються тільки відповідні системи.

К.Р. № 14

Для деякої системи даних упорядкувати маски по складності і нечіткості.

Лекція 15