Для нас такі властивості, як впорядкованість, метрична відстань і безперервність безлічі станів і параметричних множин, представляють основу для визначення найбільш істотних методологічних відмінностей на рівні змінних і параметрів. Приведемо список перенумерованих альтернатив для цих властивостей:

   0 - впорядкованості немає

 Впорядкованість: 1 - часткова впорядкованість

   2 - лінійна впорядкованість

 Відстань: 0 - не визначено

   1 - визначено

 Безперервність: 0 - дискретно

   1 - безперервно

Статус будь-якої змінної (або параметра) для цих трьох властивостей може бути однозначно охарактеризований триплетом

(впорядкованість, відстань, безперервність),

у якому кожна властивість представляється його певним значенням (або його ідентифікатором). Так, наприклад, триплет (2, 1, 0) описує дискретну змінну з лінійно впорядкованою безліччю станів, на якій визначено метричну відстань.

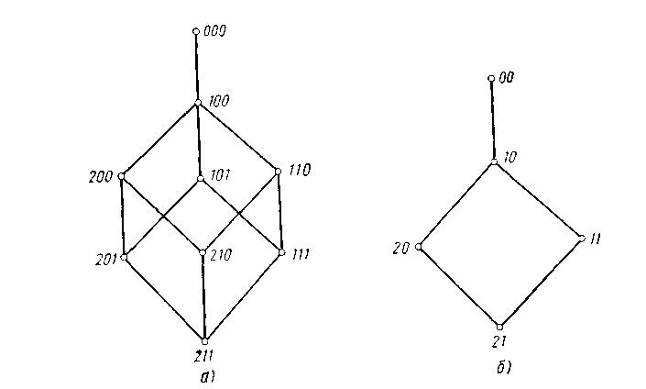
Мал. 1.2. Грати методологічних типів змінних або параметрів

Хоча дані три властивості у принципі визначають 12 можливих комбінацій, три з них (0, 0, 1), (0, 1, 0) і (0, 1, 1) сенсу не мають. Насправді, якщо на множині не визначена впорядкованість, то на ньому не можна ні змістовно визначити метричну відстань, ні розглядати його як безперервне. Таким чином, є дев'ять осмислених комбінацій. Називатимемо ці комбінації методологічними типами змінних і параметрів.

Вони можуть бути частково впорядковані за допомогою відношення «бути методологічно визначенішим чим». На мал. 1.2,а цього часткового впорядкування, створюючого грати

представлено у вигляді діаграми Хассе. Спрощені грати на мал. 1.2,б задають схему для властивостей впорядкованості і відстані, але без безперервності.

 Тепер припустимо, що є m параметрів. Вони можуть бути одного, двох, трьох (незалежно від порядку) і т.д. типів. Припустимо, що (це задоволене розумне припущення), тоді загальне число методологічних типів повного параметра визначається сумою

 (1.13)

При поєднанні цієї суми з дев'ятьма методологічними типами змінних ми одержимо загальне число можливих методологічних відмінностей однієї змінної і її параметра, це число визначається формулою.

(1.14)

Алгоритм формалізації систем об'єкту

1. Визначаються властивості ai і безліч їх проявів Ai .

2. Визначаються бази bj і безліч їх проявів Bj .

3. Визначається система об'єкту 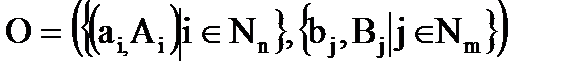, де Nn={1, 2 ., n}, а Nm={1, 2 ., m}.

К.Р. № 5

 Опишіть дві системи з різними методологічними відмінностями.

Лекція 6

2. Представляючі і початкові системи