Зупинимося детальніше на понятті каналу спостереження. Дотепер ми його визначали через функції оi і щj, визначені відповідно в рівняннях (1.6) і (1.7). Ці функції припускають розбиття безлічі Ai і Bj на деякі підмножини, позначимо їх відповідно Ai/оi і Bj/щj. Елементи будь-якої підмножини в цьому розбитті еквівалентні в тому сенсі, що вони не розрізняються з погляду введеної процедури спостереження. У такому розбитті кожна підмножина цілком представляє один стан змінної або одне значення параметра . Коли спостереження властивості ai, проводиться при деякому значенні параметра, тієї спостережуваної властивості набуває певний прояв (значення) з безлічі Ai. Цей прояв є елементом одного і лише однієї підмножини Ai/оi. Функція оi привласнює його певному стану змінної . Таким чином, передбачається, що будь-яке спостереження дозволяє нам визначити, до якої підмножини Ai/оi належить даний прояв, навіть якщо окремий прояв і не можна ідентифікувати.

Припущення про те, що відмінність підмножин Ai/оi може бути виявлена за наслідками спостережень, виправдовується тільки у тому випадку, коли помилки спостереження виключені. Подібні випадки, як показано в прикладі 1.1, зустрічаються, але відносно нечасто. При цьому підмножина Ai/оi правильно визначається у всіх випадках, окрім тих, коли фактичний прояв виявляється близько від межі між підмножинами, тобто в межах очікуваної помилки спостереження.

Оскільки властивості (принаймні деякі з них) не контролюються дослідником, неможливо запобігти прояву властивостей в небажаній близькості від меж між підмножинами Ai/оi і, отже, можна тільки скоротити можливість визначення неправильних підмножин за спостереженнями завдяки правильному вибору каналу спостереження оi . Виключити таку можливість повністю не можна.

В результаті появи можливості помилок вимірювання з проявами біля меж між підмножинами A/оi зв'язана певна невірогідність спостереження. Є два варіанти інтерпретації цієї невірогідності. Тут ми розглянемо, і дотримуватимемося одного з них.

Розбиття безлічі Ai задається функцією оi. Це те ж саме розбиття Ai/оi, що розглядалося вище. Достовірно невідомо, до якої підмножини Ai/оi належить заданий елемент Ai.. Ця невірогідність може бути задана функцією, що зіставляє будь-якій парі (елемент Ai, підмножина Ai /оi) число (звичайно між 0 і 1 - якийсь аналог вірогідності).

Визначене таким чином число в заданому контексті виражає міру достовірності того, що даний елемент належить даній підмножині.

Іншими словами все вище сказане означає, що, роблячи якесь спостереження, ми можемо стверджувати, що ми спостерігали, саме такі факти, лише з деякою вірогідністю.

Формально вищезазначена функція достовірності спостережень може бути записана таким чином

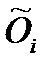 : Ai Ai 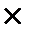/оi → [0, 1], (1.8)

О днако, оскільки кожна підмножина Ai/оi однозначно представляється (позначається) станом з множини (відповідно до функції оi), функциюможно задати в зручнішому вигляді

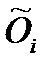 : Ai 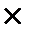 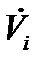 → [0, 1], (1.9)

 Визначена в рівнянні (1.9) функцияхарактерізуєт спостереження властивості ai в сенсі їх невірогідності. У цьому сенсі можна назвати нечітким каналом спостереження. Щоб уникнути непорозумінь оi називатимемо чітким каналом спостереження. „

Ясно, що для визначення нечіткого каналу спостереження необхідно спочатку задати чіткий канал спостереження оi. Чіткий канал спостереження можна також розглядати як окремий випадок нечіткого. Насправді, якщо

то задає чітку функцію з Ai в, ідентичну оi .

При розгляді баз можна ввести функцію

 : Bj  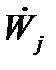  → [0, 1], (1.10)

подібну функції (1.9) і засновану на співвідношенні (1.7). Тут (x, у) - міра достовірності того, що х належить підмножині Bj/щj, який представлений значенням у параметра . На практиці, проте, ця функція не використовується.

Для будь-яких практичних потреб досить використовувати чіткий канал спостереження щj для баз, будь то група, час або простір. Проте для властивостей застосовні як чіткі, так і нечіткі канали спостереження (оi і ), і при різних обставинах більш відповідним може бути той або інший тип каналу.

Приклад 1.2. Хай властивістю ai є вік людини з групи Bj. І хай елементами Ai будуть номери років в діапазоні від 0 до 100. Покладемо, що . = { дуже молодий, молодий, середніх років, старий, дуже старий}, і хай оi - це взаємно однозначна функція Ai /оi ‹, визначена наступним

образом:

{0, 1 ..., 14} - дуже молодий

{15, 16 ..., 29} - молодий

{30, 31 …, 49} - середніх років

{50, 51 …, 74} - старий

{75, 76 …, 100} - дуже старий.

При використанні чіткого каналу спостереження дуже погано описуються люди, чий вік близький до меж між блоками Ai /оi. Наприклад, 49-річна людина позначається як людина середніх років, а 50-річний, як старий. При використанні нечіткого каналу оi, наприклад такого, який описаний на мал. 1.1, приведений виявляється більш відповідним, оскільки не дає таких різких стрибків. Важливо відзначити, що нечіткий канал спостереження дає не один стан для одного спостереження, як чіткий канал, а набір значень для всіх . Так, наприклад, при спостереженні 25-річної людини через нечіткий канал будуть набуті наступного 5 значення:

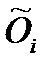( (25, дуже молодий) = 0.1

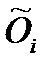( (25, молодий) = 0.97

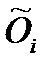( (25, старий) = 0

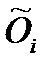( (25, дуже старий) = 0.

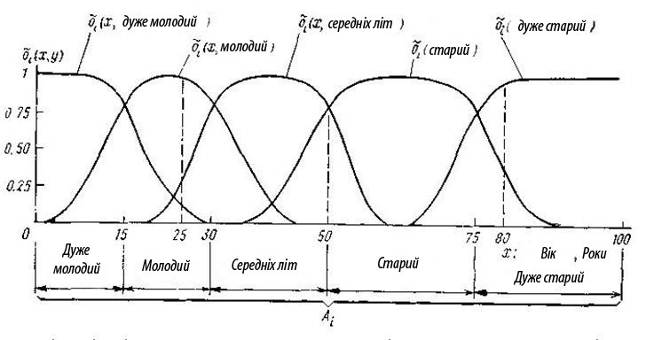
Мал. 1.1. Чіткий і нечіткий канали спостереження для повністю впорядкованої ознаки «вік людини»

К.Р. № 4

Приведіть приклад систем з чіткими і нечіткими каналами спостереження, формалізуйте їх.

Лекція 5

Методологічні відмінності

 Термін методологічна відмінність використовується тут для опису особливостей системних завдань, по яких розрізняються рівні типи завдань усередині одного типу моделей систем. Методологічні відмінності стосуються як систем, так і вимог до них.

Типи завдань, що відрізняються тільки деякими методологічними відмінностями, вимагають різних методів рішення, але мають один і той же статус в ієрархії типів моделей систем. Таким чином, методологічні відмінності є вторинними критеріями класифікації завдань наукових досліджень.

У даному розділі розглядаються методологічні відмінності, що відносяться до змінних і їх параметрів. Оскільки змінні і параметри є компонентами будь-якої системи незалежно від її типа, ці відмінності застосовні до систем всіх типів моделей.

Методологічні відмінності для змінних і параметрів - це характеристики їх безлічі станів і, відповідно, параметричних множин. Якщо змінна (або параметр) представляє властивість (або базу), то ці властивості не можуть бути довільними.

Всяка змінна пов'язана з одним або декількома параметрами, і зміни станів змінної спостерігаються на повній параметричній множині. Таким чином, комбінація властивостей безлічі станів і повної параметричної множини визначає самий елементарний тип методологічних відмінностей.

Якщо є більше одного параметра, то повна параметрична множина є декартовий твір окремих параметричних множин. Для представлення розпізнаваних властивостей цього декартова твори, властивості окремих параметрів повинні поєднуватися відповідним чином. Будемо спочатку для простоти вважати, що ми маємо справу з однією параметричною множиною незалежно від тієї, є воно окремою параметричною множиною або декартовим твором декількох, і що виділеними властивостями володіють вся ця множина.

Однією з фундаментальних методологічних відмінностей є відсутність математичних властивостей у безлічі станів або відповідної параметричної множини. Це крайній випадок, і він погано підходить для змінної (або параметра), що призначеної для представлення властивості (або бази) і має явно виражені і істотні для завдання характеристики. У літературі по вимірюваннях змінні такого роду звичайно називають змінними з номінальною шкалою.

Найбільш фундаментальною з властивостей безлічі станів і параметричних множин, що виділяються, є впорядкованість. Методологічно слід розрізняти два типу впорядкованості - часткову і лінійну.

Часткова впорядкованість - це бінарне відношення на множині (у нашому випадку на безлічі станів або параметричному), що є рефлексією, антисиметричною і транзитивною. Лінійна впорядкованість сильніше за часткову, оскільки це часткова впорядкованість, що володіє властивістю зв'язності (тобто будь-яка пара елементів множини так або інакше впорядкована).

 Формально часткова впорядкованість Q, наприклад, безліч Vi - це бінарне відношення

     Q 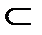 Vi  Vi ,(1.11)

що задовольняє наступним вимогам:

1. (x, x)  Q (рефлексія);

2. якщо (x, y)  Q і (y, x)  Q, то х = у (антисиметричність);

3.якщо x, y)  Q і (y, z)  Q, то ( x, z )  Q (транзитивність).

Якщо (x , y)  Q те х називається попередником у, а у - наступником х. Якщо (x , y)  Q і не існує, z  Q, такого, що ( x, z )  Q і (z, x)  Q, то х називається безпосереднім попередником у, а у - безпосереднім наступником х. На додаток до вимог рефлексії, антисиметричності і транзитивності відношення лінійної впорядкованості задовольняє наступній вимозі зв'язності: для всіх х, y  Vi, якщо 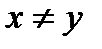, то або (x, y)  Q або (y, x)  Q. ▲

Прекрасним прикладом впорядкованості параметричної множини є час. Змінні з лінійно впорядкованою безліччю станів називаються змінними з впорядкованою шкалою.

Однією з найбільш істотних властивостей є відстань між парою елементів множини, що вивчається. Цей захід визначається функцією, що зіставляє будь-якій парі елементів цієї множини число, що визначає, на якій відстані один від одного знаходяться ці елементи з погляду деякого фундаментального впорядкування.

 ∆ Для даної множини, скажемо множини, відстань визначається функцією вигляду

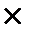
 : →R , (1.12)

Однако для того, щоб ця функція відповідала інтуїтивному уявленню про відстань, вона повинна задовольняти наступним умовам для всіх х, у, z :

( 1) (x, y) 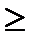 0 (умова позитивності);

( 2) (x, y) = 0 тоді і тільки тоді, коли х = у (умова нульової відстані, звана також умовою невирожденності);

( 3) (x, y) = (y, x) (симетричність);

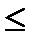
( 4) (x, y) (x, y) + (y, z) (нерівність трикутника).

Будь-яка функція, що задовольняє умовам ( 1) - ( 4), називається метричною відстанню на множині , а пара( , ) - метричним простором. Метрична відстань можна, зрозуміло, визначити як на безлічі станів, так і на параметричній множині. ▲

Прикладами змінних з вираженими і істотними метричними відстанями є майже всі змінні у фізиці, наприклад довжина, маса. Абсолютно очевидно, що і простір, і час - це параметри, до яких цілком природно застосовно поняття метричної відстані. Проте рідко вдається визначити метричну відстань на групах. Одним з таких прикладів є група студентів, лінійно впорядкована за показниками їх успішності. Змінні, з безліччю станів яких зв'язано метричну відстань, звичайно називаються метричними змінними.

Ще однією властивістю безлічі станів і параметричних множин, що має велике значення як методологічну відмінність, є безперервність. Це поняття добре відоме з математичного аналізу, і немає необхідності розглядати його тут детально.

Якнайкращим прикладом безперервного часткового впорядкування є відношення «менше або рівно», визначене на безлічі дійсних чисел або на його декартових творах. Фактично саме поняття безперервної змінної (або безперервного параметра) спирається на вимогу, щоб відповідна безліч станів (або параметрична множина) була ізоморфно безлічі дійсних чисел.

З цього виходить, що безліч станів будь-якої безперервної змінної або параметрична безліч будь-якого параметра нескінченно і незліченно. Тим самим альтернативою безперервним змінним і параметрам є змінні і параметри, задані на кінцевих множинах або, можливо, на нескінченних рахункових множинах. Останні називаються дискретними змінними або параметрами.