Якщо параметрична множина не впорядкована, то поняття параметричного сусідства не визначене, і, отже, існує тільки одна осмислена маска. Ця маска, визначувана тотожним правилом зрушення; вона називається маскою без пам'яті. Оскільки в цьому випадку є тільки одна прийнятна маска, завдання виявляється досить тривіальним [вимоги 3, 4 і 5 просто непридатні]. Це завдання зводиться до визначення для заданих даних функції розподілу вірогідності, що задовольняє вимозі 2. Вона розв'язується повним перебором даних за допомогою маски без пам'яті (в даному випадку порядок вибору не важливий) і визначення для кожного стану вибіркових змінних з (в даному випадку вони співпадають з основними змінними) числа N(c) їх появ в даних. Числа N (с) для всіх звичайно називаються частотами станів з. Вони використовуються для обчислення за деякими правилами відповідних функцій вірогідності або можливостей.
Обчислювати розподіл вірогідності по частотах можна різними способами. Так, наприклад, якщо вірогідність розглядається як характеристики даних, то звичайно обчислюються відносні частоти, тобто відносини N(c) до загального числа наявних вибірок з даних по використовуваній масці. Звідси
. 
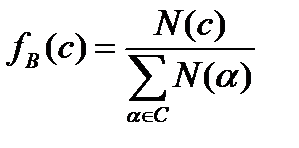(4.33)
Крім реалізації різних варіантів обчислення розподілу вірогідності необхідно також включати в обчислення якусь додаткову інформацію, пов'язану з обмеженнями на змінні. Будемо цю інформацію, що не входить у власне дані, називати додатковою. Вона може приймати самі різні форми.
Припустимо тепер, що параметрична множина повністю впорядкована. В цьому випадку з однієї і тієї ж системи даних можна одержати безліч систем з поведінкою, що відрізняється масками. Якщо для заданих даних вони визначені достатньо коректно, то вони однаково добре відповідають вимозі узгодженості. Точніше, вираз «достатньо коректний» означає, що функція поведінки добре узгоджується з даними (і, можливо, з деякою додатковою інформацією) з погляду маски і типу вибраних обмежень.
Як вже пояснювалося вище, для маски без пам'яті функцію поведінки, що добре узгоджується з даними і додатковою інформацією, можна одержати з частот станів (тобто відповідних вибіркових змінних) для даних, відображених за допомогою даної маски. Всяка маска є деяким вікном, через яке відбираються дані дані з матриці даних (або з масиву вищого порядку). При русі цього вікна уздовж всієї матриці даних частоти станів відповідних вибіркових змінних визначаються підрахунком того, як часто спостерігається кожен стан. Якщо всі вибіркові позиції перебираються, то напрям руху маски по матриці даних не має значення, проте зручніше здійснювати цей рух відповідно до встановленого на параметричній множині порядку (зліва направо або навпаки).
Для конкретних цілей одні маски можуть підходити краще, ніж інші, але ніяка маска не є правильною або неправильною.
Особливості побудови масок
Якщо дана маска є одним стовпцем (маска без пам'яті), то вибірки по всіх значеннях параметра є повними. Проте, якщо маска полягає із понад одного стовпця, то деякі вибірки на початку і кінці параметричної множини (лівий і правий краї матриці даних) виявляться неповними (див. мал. 4.2 і 4.3). Точніше, число неповних вибірок для кожного краю матриці даних рівне числу стовпців в масці мінус 1. Число стовпців в масці М називатимемо завглибшки маски і позначати . Тоді
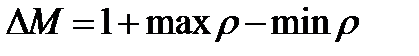(4.34)
де оператори max і min застосовані до всіх цілих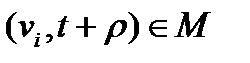 
. Так, наприклад, для маски, визначеної на мал. 4.1,, для масок без пам'яті .
Є два міркування, по яких застосування масок з великою глибиною в загальному випадку небажано.
1. якщо маска використовується для породження даних, то чим більша її глибина, тим більше потрібна початкова умова. Це, взагалі кажучи, не бажано.
2. якщо маска використовується для вибірки даних, то число неповних вибірок рівне . Це означає, що із зростанням глибини маски все менше наявних даних використовується для визначення функції поведінки. Отже, із збільшенням глибини маски звужується емпірична основа, на якій будується функція поведінки. Це, зрозуміло, також небажано.
Обидва ці міркування, а також практичні міркування, пов'язані з складністю обчислень, призводять до того, що глибина маски звичайно вибирається не дуже великою. Таким чином, представляється доцільним визначити обмеженість глибини маски як вимогу 1 для даного типа завдань. Це можна зробити, визначивши найбільшу допустиму маску, скажемо маску М як декартовий твір
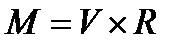(4.35)
де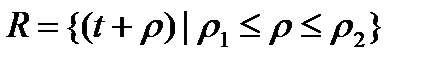 
.
Подібна маска може бути представлена у вигляді повної матриці з п рядками і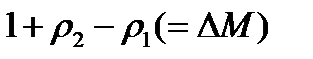 
стовпцями. Називатимемо її М-матрицею. Якщо спочатку задано тільки, але не конкретні значення і, то доцільно вибирати для них якісь стандартні значення, наприклад, 
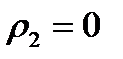,а 
.
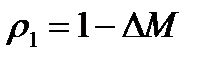Змістовні підмаски
При заданій найбільшій допустимій масці М всі її змістовні підмаски утворюють обмежену безліч Yr систем з поведінкою. Термін «змістовна підмаска» характеризує підмаски М, що задовольняють наступним вимогам:
(ml) у підмаску входить принаймні один елемент з кожної підмаски, визначеної рівнянням (4.10) (тобто один елемент з кожного рядка М-матриці);
(m2) у підмаску повинен бути включений принаймні один елемент з правилом зрушення (крайній правий елемент з М-маски).
Вимога ml необхідна для покриття заданої системи даних, тобто для того, щоб гарантувати, що будь-яка базова змінна із заданої системи даних була б включена в будь-яку з систем з поведінкою з обмеженої безлічі Yr. Вимога m2 перешкоджає дублюванню еквівалентних підмасок, тобто підмасок, що перетворюються одна в іншу тільки за допомогою додавання константи до правила зрушення (зрушення ряду в М-масці).
Можна легко одержати формулу для числа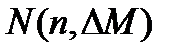 
змістовних підмасок найбільшої допустимої маски, де n - число базових змінних, а - глибина маски М:
. 
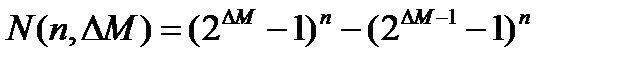(4.36)
Перший член виразу (4.36) задає число підмасок М, що задовольняють умові ml, а другий член - число масок, що порушують умову m2. У табл. 4.1 приведені значення при п .
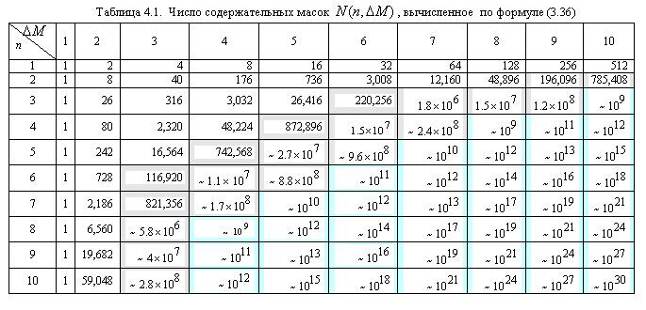
Ця таблиця розділена на три області, для яких розміри найбільшої допустимої маски представляються: а) що легко піддаються обчислювальній обробці (ліва верхня область); би) що у принципі піддаються обробці, що зажадає тривалої роботи дуже могутнього комп'ютера (середня область); у) що не піддаються обчислювальній обробці (права нижня область). Ці області показані тільки для найбільш типового випадку. Так, наприклад, якщо є в розпорядженні могутня система паралельних обчислень, то область випадків, що піддаються обчислювальній обробці, може бути розширена майже удвічі.
Якщо число змістовних масок виявляється дуже велике, щоб піддаватися обчислювальній обробці, АСНД повинні враховувати можливі додаткові обмеження, що накладаються на найбільшу допустиму маску. Такими обмеженнями можуть бути, наприклад, наступні:
1. фіксація безлічі породжуваних вибіркових змінних;
2. фіксація числа вибіркових змінних;
3. фіксація верхньої межі числа вибіркових змінних;
4. обмеження, при якому розглядаються талько маски без пропусків (прикладом пропуску є елемент, що ідентифікується координатами, в масці, зображеній на мал. 4.1,а).
Подібні обмеження або їх комбінації істотно скорочують множину, і таким чином, збільшують розмір найбільших допустимих масок, що піддаються обчислювальній обробці.
К.Р. № 12
Виходячи з деякої системи даних, побудувати функцію поведінки, у разі масок без пам'яті.
Лекція 13
Заходи нечіткості
Ступінь недетермінованої повинен вимірюватися узагальненою нечіткістю, супутньою породженню даних. А значить, вона повинна бути визначена через функції поведінки, що породжують, і для нейтральних і направлених систем з поведінкою. Якщо ці функції є функціями розподілу вірогідності, то міра узагальненої нечіткості добре відома - це шенноновськая ентропія
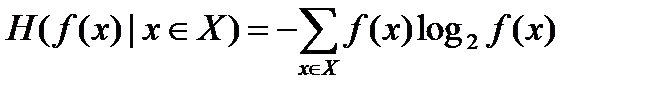
Вона вимірює нечіткість в одиницях, званих бітами.
Якщо припустити, що будь-яка кінцева множина X дані альтернативні вихідні значень характеризується певним розподілом вірогідності, то зручніше спростити позначення і писати замість .
Легко бачити, що
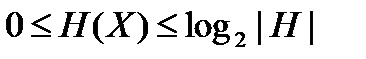(4.38)
Нижня межа досягається у тому випадку, коли вірогідність всіх вихідних значень, за винятком одного, рівна 0; верхня межа досягається тоді, коли вірогідність всіх подій однакова, тобто рівні . Відношення ентропії до її верхньої межі
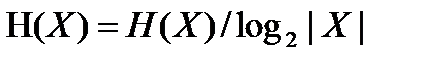(4.39)
називається нормалізованою ентропією; зрозуміло, що
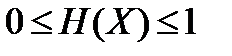(4.40)
У нашому випадку безліччю виходів є множини а розподіли вірогідності представляються функціями поведінки, визначуваними відповідно формулами (4.11) (4.17) (4.27) (4.30). Для спрощення запису опустимо індекси В і GB, а також знак ^ . Таким чином
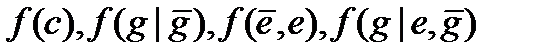(4.41)
позначає вірогідність, визначувана відповідно формулами (4.11) (4.17) (4.27) (4.30); сенс будь-якого з цих позначень однозначно визначається укладеними в дужки аргументами. Крім того, визначимо безумовну вірогідність
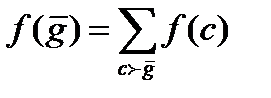(4.42)
де указує на те, що є підмножиною стану з (підстаном з); формально, якщо
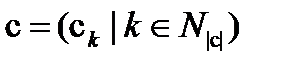(4.43)
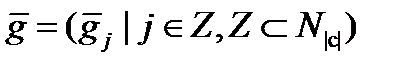(4.44)
то тоді і тільки тоді, коли для всіх . Для направлених систем безумовна вірогідність обчислюється по небагато зміненій формулі
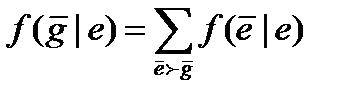(4.45)
Умовна вірогідність, що характеризує процес породження даних, пов'язана з основною (сумісними) і безумовною вірогідністю таким чином:
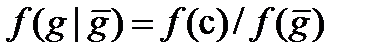(4.46)
. 
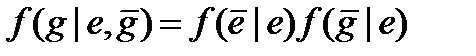(4.47)
Перша формула описує цей зв'язок для нейтральних, а друга - для направлених систем.
Методи обчислень нечіткості
При заданій масці, що породжує, для нейтральної системи, через яку визначається безліч станів вибіркових змінних, що генеруються і генеруючих, нечіткість, що породжує, визначається як середня нечіткість, що базується на вірогідності, зважених вірогідністю умов, що породжують:
. 
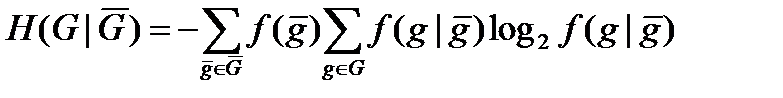(4.48)
Це значення визначає ступінь недетермінованої системи, що даної нейтральної породжує, з поведінкою.
Для направлених систем нечіткість, що породжує, обчислюється за формулою
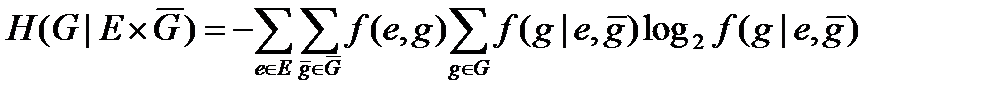(4.49)
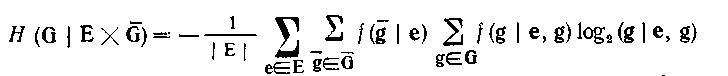
яку можна безпосередньо застосовувати у тому випадку, коли можна і має сенс визначати вірогідність, тобто коли направлена система одержана з нейтральної. Якщо ми не маємо в своєму розпорядженні вірогідності станів елементів безлічі Е або ця вірогідність неістотні, тоді як базова вірогідність береться вірогідність [аналог вірогідності f(c) для нейтральних систем], виходячи з якої обчислюється решта необхідної вірогідності. В цьому випадку нечіткість обчислюється формулі (4.50)
де вірогідність і обчислюються по заданій вірогідності згідно формулам (4.45) і (4.47).
Формули (4.48), (4.49) і (4.50) можна замінити іншими, зручнішими для обчислення. Наприклад, рівняння (4.48) можна модифікувати таким чином:
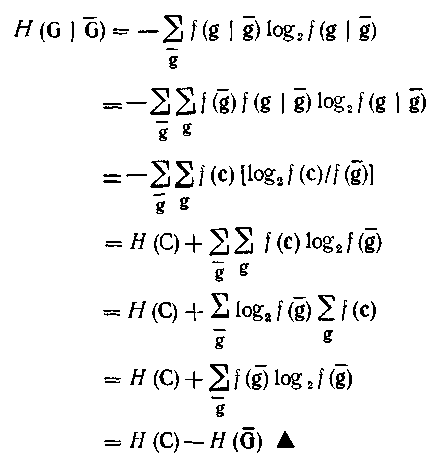
Таким чином, можна обчислити, не використовуючи умовну вірогідність, по формулі
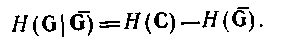(4.52)
Так само рівняння (3.49) і (3.50) можна замінити відповідно рівняннями
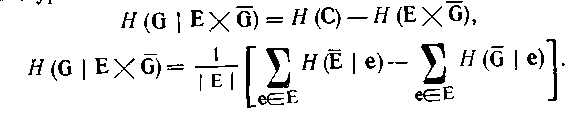(4.53)
Максимальне значення нечіткості будь-якого типа, що породжує, рівне; отже, нормалізована нечіткість, що породжує, виходить діленням нечіткості, що породжує, на її максимальне значення. Наприклад
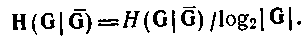
Приклад 4.2. На мал. 4.5,а показана імовірнісна функція поведінки для чотирьох вибіркових змінних кожна з двома станами - 0 і 1. Стани з нульовою вірогідністю в таблиці не приводяться. Вибіркові змінні визначені через дві базові змінні за допомогою маски, зображеної на мал. 3.7,а. Оскільки вибіркові змінні суть зрушення однієї і тієї ж базової змінної, розподіли вірогідності їх станів повинні бути однакові; вони і справді однакові; обидва мають вірогідність 0.7 і 0.3 відповідно для станів 0 і 1. Аналогічно змінні (зрушення) мають однаковий розподіл вірогідності: 0.6 і 0,4 відповідно для станів 0 і 1. Отже, для даної маски приведена функція розподілу вірогідності є коректною функцією поведінки.
Якщо дана система інтерпретується як нейтральна, її нечіткість, що породжує, може бути обчислена за формулою (4.52). Для першого члена формули ми маємо
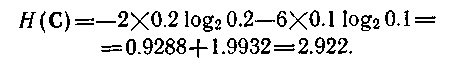
Значення другого члена залежить від порядку породження і від відповідної маски. На мал. 4.5,в і г показані два можливі порядки породження. Для породження зліва направо маємо
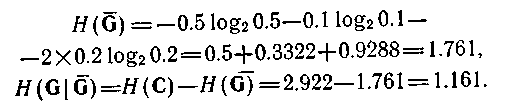
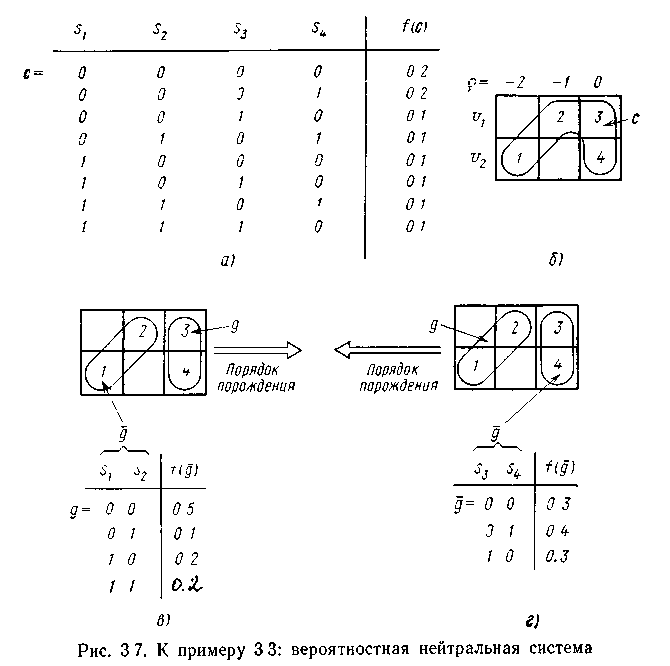
Мал. 4.5 Імовірнісна нейтральна система
Для іншого порядку породження (мал. 4.5,г) ми одержимо
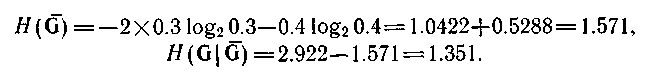
Отже, нам можна вибрати один з двох порядків породження; перший порядок переважно, оскільки має нижчу породжувану нечіткість. Оскільки в даному прикладі, то нормалізовані значення тих, що обчислювальних породжують нечеткостей виходять діленням їх на два.
В деяких випадках застосуємо тільки один порядок породження. Якщо, наприклад, параметром є час, то у кожному випадку має сенс тільки один з порядків, визначуваний метою використання системи з поведінкою. Якщо вона використовується для прогнозу, то стани повинні породжуватися у порядку зростання часу (зліва направо); якщо ж вона використовується для ретроспекциі, то стани повинні породжуватися у порядку убування часу. У даному прикладі, якщо параметром є час, то виявляється легшим передбачати майбутні стани системи, чим визначати минулі.
Припустимо тепер, що інтерпретується як вхідна змінна і що по функції поведінки на мал. 4.5,а визначена відповідна направлена система. Тепер для обчислення нечіткості, що породжує, можна скористатися формулою (4.53). Нечіткість вже була обчислена раніше;зависит від порядку породження. У будь-якому випадку безліч Е представляється станами переменнихпредставляєтся або станами (у порядку зростання параметра) або станами (у порядку убування параметра). У першому випадку нечеткостьсвязана із змінними
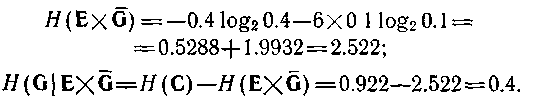
У другому випадку вона представляє нечіткість змінних:
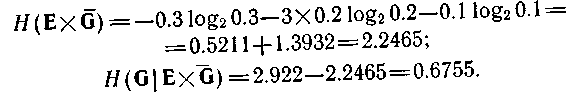
Таким чином, знову виявляється, що передбачати майбутні стани легше, ніж визначати минулі.
Припустимо тепер, що ми не маємо в своєму розпорядженні ніякої інформації щодо вхідної змінної або що ця інформація неістотна (наприклад, у тому випадку, коли контролюється користувачем). Тоді всі обчислення повинні проводитися для приведеної на мал. 4.6,а умовної вірогідності. Як показано на цьому малюнку, список вірогідності разбітна чотири частини, відповідні різним станам е. Нечіткості для кожного стану також приведені на мал. 4.6,а. Тут же показано розбиття маски на
Ситуація при породженні станів зліва направо, включаючи значення для кожного стану е, показана на мал. 4.6,в.
З формули (4.53) одержимо
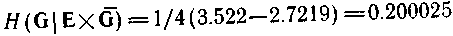
Інший порядок породження зображений на мал. 4.8,г. Для нього маємо
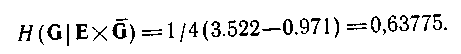
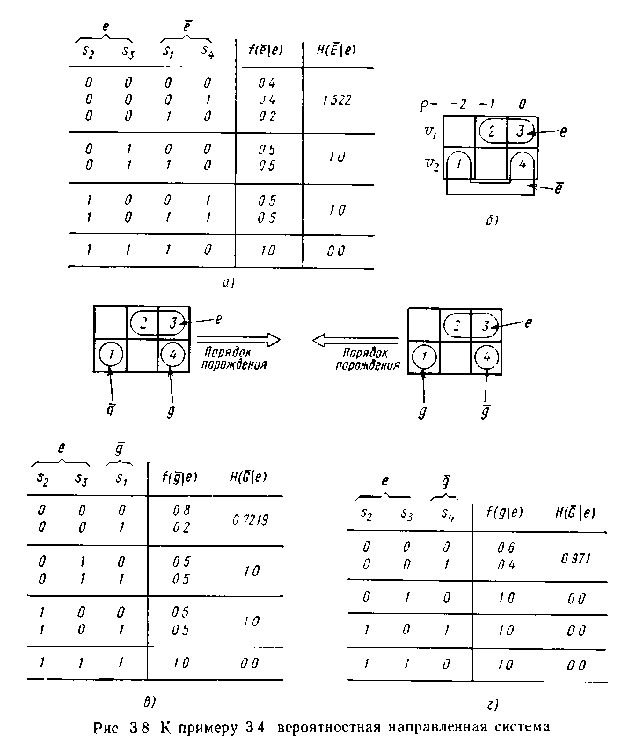
Мал. 4.6 Імовірнісна направлена система
К.Р. № 13
Розрахувати ту, що породжує нечіткість для випадку направленої і нейтральної системи з поведінкою. Розглянути обидва порядки породження.
Лекція 14
Дата: 2019-03-05, просмотров: 285.
