Розглянемо спочатку поняття маски і пов'язана з ним поведінка представляючих систем для повністю впорядкованих параметричних множин, а потім розповсюдимо його на частково впорядковані параметричні множини. Позначимо повністю впорядковані параметричні множини, а їх елементи . При цьому рівняння (4.4) трохи зміниться:

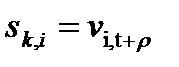 (4.9)

Для повністю впорядкованих параметричних множин маска може бути зображена у вигляді вирізки з матриці, що представляє декартовий твір .Это показано на рис.4.1,а, на якому рядки помічені ідентифікаторами

Рис.4.1. Пояснення поняття маски для повністю впорядкованих параметричних множин.

змінних з множини V, а стовпці - цілими константами, пов'язаними з правилами зрушення вигляду (4.2). Елементи матриці або порожні, або є ідентифікаторами до вибіркових змінних, приписані парам згідно (4.6); порожні елементи матриці відповідають елементам, що не входять в маску. У візуальному уявленні стає ясно, чому використовується термін «маска».

Часто буває зручно розбити маску М на підмаски М„ кожна з яких пов'язана з однією змінною і, з подібної системи. Формально

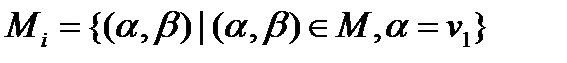 (4.10)

У візуальному (матричному) представленні підмаски є рядками. У будь-якій масці один стовпець відповідає тотожному правилу зрушення . Цей стовпець має особливе значення, оскільки пов'язані з ним вибіркові змінні ідентичні базовим змінним заданої представляючої системи. Будемо цей стовпець в масках називати довідником. Якщо маска поміщена на матрицю даних таким чином, що довідник співпадає з певним значенням t, то маска виділить тільки деяку підмножину елементів, а саме елементи, що представляють повний стан вибіркових змінних при даному значенні t. Так, наприклад, на мал. 4.1,б зображена маска (визначена на мал. 4.1,а), поміщена на матрицю даних d при t=7 (довідник маски співпадає з t=7). Повний стан вибіркових змінних для цього положення маски показаний на мал. 4.1,в. Стану довідника вибіркових змінних в точності ті ж (для будь-якого t), що і стан базових змінних відповідно . Решта вибіркових змінних є станами з параметричного сусідства в t. Для будь-якої маски при будь-якому t схема сусідства зберігається. Якщо t - час, то змінна представлятиме майбутній (щодо даного значення t) стан змінної, а змінні і представлятимуть, минулі стани змінної будь-яка маска представляє певну точку зору, відповідно до якої представляються обмеження на базові змінні.

К.Р. № 9

Опишіть систему з поведінкою у разі повністю впорядкованих параметричних множин. (Обов'язково необхідно вказати маски і вибіркові змінні.)

Лекція 10

4.4 Функції поведінки. Змінні, що породжують і породжувані.

Найпростіший спосіб завдання певної маски - це перелік всіх повних станів відповідних вибіркових змінних. У загальному вигляді подібний перелік є підмножиною декартова твори З, тобто багатовимірним відношенням, визначеним на С. Это відношення визначається функцією

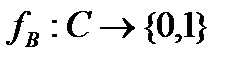
такий, що, якщо стан з входить в перелік, і інакше. Така функція дає деякі відомості про поведінку вибіркових змінних, функцію звичайно називають функцією поведінки. Функція, визначувана рівнянням (4.11), задає тільки одного з існуючих типів функцій поведінки, що різними способами описують обмеження на змінні.

Функція визначає стани, що зустрічаються, з, але не визначає значення параметра, при якому вони мають місце. Таким чином, ця функція є параметрично інваріантною.

Система, що характеризує параметрично інваріантне обмеження на безліч змінних через функції поведінки, визначається трійкою

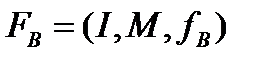 (4.12)

де I - узагальнена представляюча система; М - маска, визначена на I; -функция поведінки, визначена через М і I. Таку систему називатимемо системою з поведінкою

Не дивлячись на те, що будь-яка система з поведінкою, визначувана (4.12), якимсь конкретним параметричні інваріантно описує обмеження на змінні представляючої системи, вона не містить опису того, як використовувати це обмеження для породження даних. Для розробки такого опису потрібно розбити вибіркові змінні на дві підмножини:

1) змінні, стани яких породжуються з обмеження; назвемо їх породжуваними змінними;

2) змінні, стани яких використовуються як умови в процесі генерації, назвемо їх змінними, що породжують.

Для заданої системи з поведінкою одним із способів визначення породжених змінних, що породжують, є визначення для даної маски М двох підмасок і . Будемо

 (4.13)

Де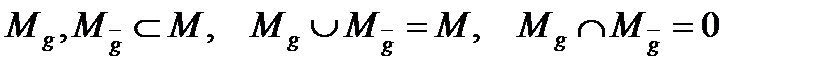

називати маскою породження, тобто це маска М і її розбиття на породжувану підмаску і що породжує підмаску .

По аналогії з розбиттям на і безліч ідентифікаторів вибіркових змінних можна розбити на дві підмножини, скажемо і, що представляють ідентифікатори відповідно породжуваних змінних, що породжують. Для зручності позначень кодуюча функція (4.7) може бути замінена двома функціями

 (4.15)

за допомогою яких безліч станів і відповідно породжуваних змінних, що породжують, задаються декартовими творами

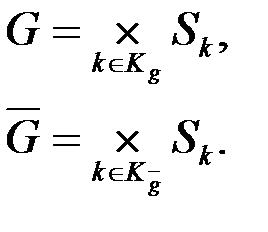 (4.16)

Тепер спосіб представлення стану породжуваних змінних (скажімо ), визначуваного за станом змінних (скажімо ), що породжують, можна виразити функцією

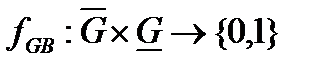 (4.17)

де

(4.18)

Назвемо цю функцію функцією поведінки, що породжує.

Якщо маску М і функцію з (4.11) замінити відповідно на і функцію, то вийде альтернативна система

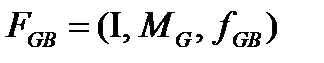.  (4.19)

Називатимемо таку систему системою, що породжує, з поведінкою.

Використання системи, що породжує, з поведінкою для породження даних включає наступні два етапи:

а) для деякого значення задано стан ; для визначення стану при тому ж значенні використовується функція ;

б) значення t замінюється на нове і повторюється етап а).