1. На етапі а) неявно передбачається, що при заданому значенні t стан відомий. Цей стан називається початкова умова. Проте після цього все повністю визначається самим процесом породження, тобто станами і g, пов'язаними з попереднім значенням t. При цьому передбачається, що значення t повинні на етапі (б) змінюватися відповідно до порядку, заданого на множині Т. Таким чину, значення t замінюються або на t+l, або на t-1. У першому варіанті початкова умова повинна бути визначена для найменшого можливого значення t, а в другому - для найбільшого можливого значення t.

2. З необхідності породження даних в одному з двох порядків витікає, що існує тільки два змістовне розбиття маски М на і, кожне з яких відповідає одному з двох порядків породження. Якщо дані породжуються у порядку зростання (убування) t, то містить рівно по одному елементу кожної підмаски, визначеної (4.10), елемент з найбільшим (найменшим) значенням ; решта елементів М входить в . Таким чином, графічно виходить, що - це безліч найправіших елементів М (правий край цієї маски) або, навпаки, безліч найлівіших елементів М (лівий край маски).

3. Передбачається, що для будь-якого стану є принаймні один стан, допустимий функцією [тобто ] Якщо допускається тільки один стан, то для будь-якої початкової умови дані породжуються однозначно; такі системи називаються детермінованими. Якщо допускається більш ніж один стан, то породження даних проблематично, оскільки породжуваний стан не завжди однозначний визначено. Для таких систем вибираючі функції поведінки не підходять. Змістовніше вони описуються функціями поведінки інших типів, що розглядаються нижче. Для детермінованих систем представлення (4.17) функції поведінки, що породжує, може бути замінено простішим

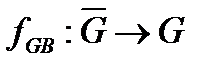.  (4.20)

Приклад 4.1. Для пояснення процесу породження даних системою, що породжує, з поведінкою типа, визначуваного рівнянням (4.12), покладемо, що подібна система складається з впорядкованої параметричної безлічі і п'яти змінних, стани яких будуть визначені нижче. Скористаємося маскою, заданою на мал. 4.2. Дані можуть породжуватися або у порядку зростання, або у порядку убування значень параметра t. Обидва ці варіанти показані відповідно на мал. 4.2 і 4.3.

У першому випадку (мал. 4.2) породжувані вибіркові переменниє- це змінні, відповідні правому краю маски, тобто 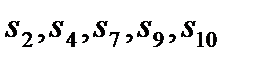; решта вибіркових змінних є такими, що породжують. Породження даних в матриці даних відбувається зліва направо. Хай функція поведінки, що породжує, представлена у вигляді (4.20), визначається рівняннями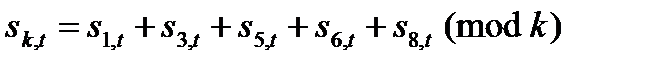

При 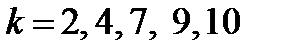, Безліч станів породжуваних змінних визначається цими рівняннями, а безліч станів змінних, що породжують, - їх положенням в масці. Наприклад, безліч станів породжуваної змінної - це 0, 1, 2, 3, оскільки рівняння для береться по модулю 4; змінна, що породжує, має ту ж безліч станів, що і s4, оскільки обидві ці змінні визначені через одну і ту ж змінну представляючої системи (тобто  ).

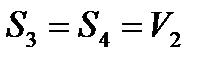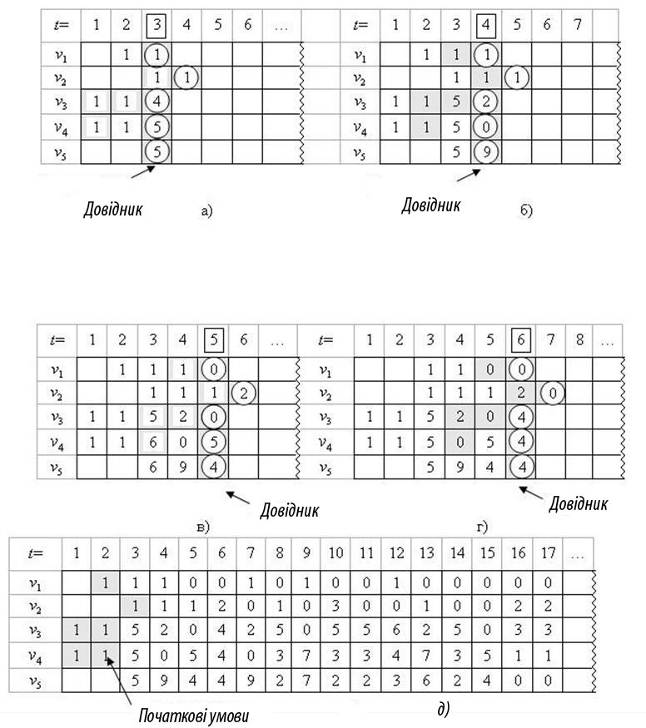
Мал. 4.2. Дані, породжені у порядку зростання значення параметра t (Приклад 3.1).

Першою осмисленою позицією маски на матриці даних (позиція визначається положенням довідника маски) є позиція t=3; позиції t=1 і t=2 сенсу не мають, оскільки стани деяких вибіркових змінних для цих позицій не визначені ( не входить в безліч Т). Початкова умова складається з шести елементів матриці даних: 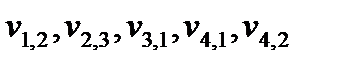 . Хай, наприклад, всі ці елементи рівні 1. Ще п'ять елементів матриці даних - 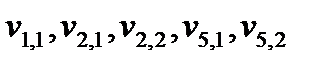- не можуть бути породжені, а можуть бути задані користувачем, але для породження даних ці змінні не потрібні. На мал. 4.2,а,б,в,г детально показано породження станів відповідно для t = 3, 4, 5, 6; кухлями обведені породжені стани. На мал. 4.2.д показане початкова умова і дещо більший фрагмент породженої матриці даних.

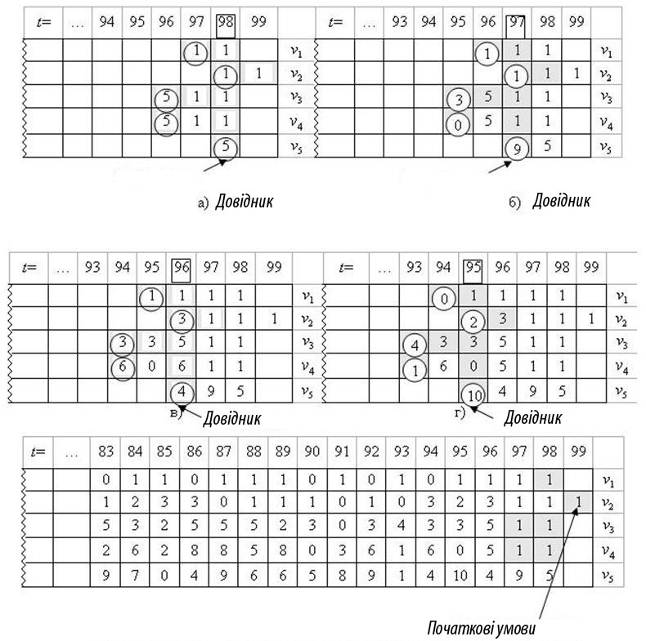
Мал. 4.3. Дані, породжені у порядку убування значення параметра t (Приклад 3.1).

Якщо дані породжуються у порядку убування t (див. мал. 4.3), то породжуваними змінними є змінні 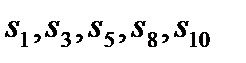, представляючі лівий край маски, тобто змінні . Дані в матриці даних породжуються справа наліво. Припустимо тепер, що визначається рівняннями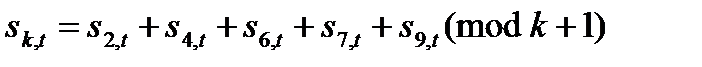

при до = 1, 3, 5, 8, 10. Породження даних при t = 98, 97, 96, 95 детально показане на рис.4.3,а, би, в і р. На мал. 4.3,д показано початкову умову і дещо більший фрагмент породженої матриці.

К.Р. № 10

Для деякої системи з поведінкою, опишіть функції поведінки. Приведіть приклад процедури породження даних.

Лекція 11