Завдання наукових досліджень

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

АСНД - конспект лекцій

Лекція 1

Введення 2

Завдання наукових досліджень 2

Систем і їх типи 3

1. Загальні поняття і визначення

Лекція 2

1.1 Об'єкти і системи об'єктів 4

1.2 Базові властивості 5

1.3 Обмеження на вибір баз 5

1.4 Формальне визначення системи 6

Лекція 3

1.5 Змінні і параметри 6

1.6 Узагальнені змінні і параметри. Формалізація. 7

Лекція 4

1.7 Канали спостереження 8

1.8 Нечіткі канали спостереження 9

Лекція 5

1.9 Методологічні відмінності 11

1.10 Методологічні відмінності на рівні змінних і параметрів 13

2. Представляючі і початкові системи

Лекція 6

2.1 Формалізація представляючих і початкових систем 14

2.2 Системи з вхідними і вихідними змінними 16

Лекція 7

2.3 Вироджені типи направлених систем 17

3. Системи даних

Лекція 8

3.1 Формалізація систем даних 21

3.2 Системи даних з нечіткими каналами спостереження 22

3.3 Представлення даних 22

4. Породжуючі системи

Лекція 9

4.1 Системи з поведінкою 23

4.2 Вибіркові змінні і маски 24

4.3 Маски у разі повністю впорядкованих параметричних множин 25

Лекція 10

4.4 Функції поведінки. Змінні, що породжують і породжувані. 26

4.5 Особливості процедури породження даних 27

Лекція 11

4.6 Функції породження для недетермінованих систем 30

4.7 Направлені системи з поведінкою 31

Лекція 12

4.8 Перехід від систем даних, до систем з поведінкою 32

4.9 Особливості переходів, залежно від властивостей параметричної множини 33

4.10 Особливості побудови масок 34

4.11 Змістовні підмаски 34

Лекція 13

4.12 Заходи нечіткості 35

4.13 Методи обчислень нечіткості 36

Лекція 14

4.14 Вибір відповідних систем з поведінкою 40

4.15 Впорядкування по складності і нечіткості 41

Лекція 15

4.16 Системи із станами, що змінюються 45

Лекція 16

4.17 Взаємозв'язок ST-систем і систем з поведінкою 49

Лекція 17

4.18 Види систем, що породжують 52

4.19 Спрощення систем, що породжують 53

Лекція 18

Дослідження і проектування за допомогою АСНД 56

Лекція 1

Введення

Наукові дослідження дозволяють виявляти і досліджувати неявні якості і закономірності властиві досліджуваним об'єктам. До таких об'єктів, найчастіше відносяться певні системи і процеси. Особливий інтерес для науки і прикладних завдань представляє автоматизація наукових досліджень, тобто створення автоматизованих систем наукових досліджень (АСНД).

В курсі будуть розглянуті загальні принципи формалізації довільних систем, отримання емпіричних даних в ході моделювання, основи дослідження систем. Тобто принципи побудови і застосування АСНД.

Систем і їх типи

Під типами систем розуміємо кількості використовуваних знань про ці системи. Чим старший тип, тим точніше модель (система) описує реальний об'єкт і тим більше глибокі наукові дослідження можуть бути проведені. Всі типи систем будуть розглянуті надалі. Їх вивчення буде нашим основним завданням.

Типи систем можуть бути зображені на наступній ієрархічній схемі, мал. 2. Початкові системи є формальним описом об'єктів зовнішнього світу. Системи даних, припускають засоби для опису даних різної природи, одержаних від об'єкту. Системи, що породжують, включають засоби породження даних адекватних об'єкту дослідження. Структуровані системи складаються з наборів систем нижчого рівня.

У системах вищого рівня використовуються знання нижчих рівнів, і, крім того, міститися знання недоступні нижчим рівням. Таким чином, початкова система міститься у всіх вищих рівнях.

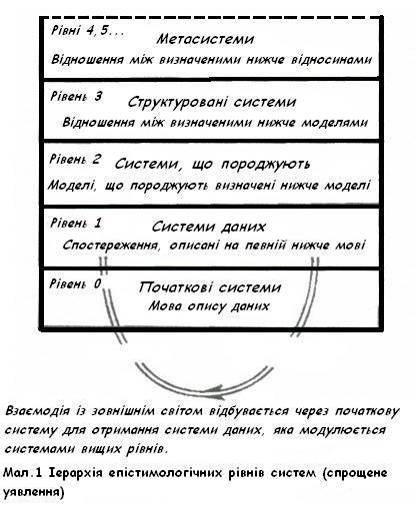
Рис.2 Ієрархічна схема типів систем

К.Р. № 1

Охарактеризуйте загальну схему роботи АСНД, і ієрархічні типи систем.

Лекція 2

1. Загальні поняття і визначення

Об'єкти і системи об'єктів

У даному курсі під об'єктом розуміємо частину світу, що виділяється як єдине ціле протягом відчутного проміжку часу.

Згідно цьому визначенню об'єкти можуть бути як

а) матеріальними, так і

б) абстрактними.

Потім, можна матеріальні об'єкти розділити на природні (такі, як шматок скелі, клітка організму, сонце) і створені людиною (такі, як аеропорт, обчислювальний центр). Абстрактні об'єкти (такі, як музичний твір, конспект або конституція України) звичайно створюються людиною, проте деякі з них можна розглядати і як природні, принаймні, до деякої міри (наприклад, український або будь-яка інша природна мова).

В більшості випадків об'єкти володіють практично нескінченним числом властивостей, будь-яке з яких можна цілком осмислено вивчати. Отже, будь-який об'єкт неможливо вивчити повністю. Це означає, що необхідно відібрати обмежене (і звичайно досить мале) число характеристик, що найкращим чином описують даний об'єкт як явище. Після того, як такий відбір зроблений, необхідно визначити процедуру кількісного вимірювання кожної властивості. Що позначає, введення якихось абстрактних змінних, що представляють певні властивості.

На об'єкті, що цікавить нас, система задається набором відповідних властивостей об'єкту. Кожному з яких призначаємо певну змінну, яка може бути зафіксована і зміряна.

Таким чином, система завжди розглядається не як реальний об'єкт, а як абстрагування або відображення деяких властивостей об'єкту.

Тепер потрібно пояснити те, як слід задавати систему. Наприклад, розглянемо мідний дріт, як систему. Реальний дріт, характеризується не тільки завдовжки і положенням, але і масою, температурою, електропровідністю, кристалічною структурою, хімічними домішками, радіоактивністю, швидкістю, межею міцності на розтягування, поглинанням світла, пружністю, формою, питомою вагою і т.д. і т.п. Нереально було б досліджувати всі ці параметри одночасно, так такі спроби ніколи і не робляться. Потрібно виділити і вивчити параметри, що відносяться до якоїсь головної проблеми, яка вже визначена. Таким чином, можна охарактеризувати систему таким чином, система - це не предмет, а список змінних.

Нагадаємо, що термін «змінна» використовується тут для позначення деякої властивості. Тому, щоб можна було визначити його точно, потрібно спочатку розібратися, що ж така властивість.

Базові властивості

Відмітимо, що з кожною властивістю пов'язано безліч його проявів. Так, наприклад, якщо властивістю є успішність студента, то проявом цієї властивості можуть бути відповідні характеристики.

При одиничному спостереженні властивість має один конкретний прояв. Для визначення можливих проявів цієї властивості, потрібно реалізовувати безліч спостережень цієї властивості. Для того, щоб розрізняти спостереження, здійснювані за допомогою однієї і тієї ж процедури, потрібне щоб кожне спостереження чимось відрізнялося від інших. Будь-яку властивість, використовувану для визначення відмінностей в спостереженнях однієї і тієї ж властивості, називатимемо базою.

Наприклад, в машинному експерименті одержуємо емпіричну вибірку, прояви деякої змінної, шляхом отримання набору випадкових чисел. Кожен конкретний досвід можна відрізнити від іншого за часом почала проведення досвіду.

Слід підкреслити, що поняття якоїсь базової властивості завжди супроводить вивченню деякої основної властивості.

В деяких випадках різні спостереження однієї і тієї ж ознаки за часом невиразні (тобто або зроблені одночасно, або час взагалі не має значення), зате відрізняються положення в просторі, в яких зроблені спостереження. Наприклад, різні властивості, що характеризують стан різних промислових роботів деякого автоматизованого виробництва, розташованих в різних точках простору.

Час і простір не єдино можливі бази. Множинні спостереження однієї і тієї ж властивості можуть розрізнятися один від одного по індивідах якоїсь групи, на якій визначено дану властивість. Це може бути соціальна група, наприклад група студентів, на якій розглядається властивість успішності; група вироблюваних товарів певного типа, безліч слів в якомусь тексті і т.д.

Бази трьох основних типів - час, простір, група - можна комбінувати. Хоча у принципі можливі будь-які комбінації, особливо важливі і поширені комбінації час - простір і час - група.

Приклад часу-групи: властивості, що характеризують положення в економіці, політиці і суспільстві різних країн, спостерігаються різними організаціями.

Крім особливого використання часу, простору і груп як бази, вони можуть виступати і як властивості. Наприклад, щоденне спостереження максимального часу запізнення студентів на пари.

Обмеження на вибір баз

Приведені приклади показують, що вибір відповідних баз достатньо гнучкий, проте абсолютно не довільний. Обмеження при цьому виборі достатньо точно виражені в описаних нижче вимогах, яким повинні задовольняти правильно вибрані бази.

Перше, бази повинні бути застосовні до всіх властивостей системи, для якої вони визначені. Наприклад, простір не застосовно для характеристики властивостей музичного твору.

Друге, бази системи повинні відповідати призначенню, для якого визначається дана система. Так, наприклад, при спостереженні за студентами після введення нових учбових нормативів спостерігають за відповідними ознаками. Ясно, що єдиної відповідними для цього базами є час і група.

Третє, спостереження всіх властивостей системи повинні однозначно визначатися базами системи, тобто кожен елемент базової множини (значення певного моменту часу, точка простору, елемент групи або відповідна комбінація елементів) визначає одне і лише один прояв будь-якої з властивостей. Наприклад, при дослідженні властивостей слів тексту цілком розумною базою є група слів, що входять в цей текст. Очевидно, що така база застосовна до цих властивостей і відповідає меті дослідження. Проте вона не задовольняє вимозі однозначного розрізнення спостережень. Насправді, одне і те ж слово може знаходитися в одній і тій же позиції і мати ту ж функцію в декількох пропозиціях в даному тексті. Для того, щоб відрізнити будь-яке спостереження, нам потрібно звернутися в даному випадку до одновимірного абстрактного простору, точкою якого є положення слова в тексті.

К.Р. № 2

Охарактеризуйте поняття базової властивості, приведіть докладний приклад.

Виберіть деяку систему, і формалізуйте її.

Лекція 3

Змінні і параметри

Змінною називається представлення властивості, тобто образ властивості, визначуваний конкретною процедурою спостереження або вимірювання. Кожна змінна має певне ім'я, що відрізняє її від інших даних змінних, і зв'язується з певною безліччю величин, через які вона себе проявляє. Ці величини звичайно називають станами, (або значеннями) змінною, а вся множина - безліччю станів.

Аналогічно параметром називається операційне представлення бази. Кожен параметр має унікальне ім'я, і з ним зв'язується якась множина; називатимемо його параметричною множиною, а його елементи - значеннями параметра.

По аналогії з властивостями і базами передбачається, що різні спостереження однієї і тієї ж змінної розрізняються по значеннях параметрів. Якщо використовуються два і більш параметра, то їх загальною параметричною множиною є декартовий твір окремих параметричних множин. Необхідно, щоб кожне конкретне значення параметра (із загальної параметричної множини) ідентифікувало одне і лише одне спостереження відповідних змінних.

На окремій безлічі станів або параметричних множинах можуть бути визначені деякі математичні відносини, скажімо, відношення порядку або відстань. Простим прикладом відношення порядку, є відношення між числами розташованими на звичайній числовій осі. Подібні відносини відображають фундаментальні характеристики властивостей і баз в тому ступені, в якій вони властиві відповідним вимірювальним процедурам.

Відмінності в подібних властивостях серед змінних або параметрів, які мають істотне методологічне значення, тобто впливають на методи досліджень, називатимемо методологічними відмінностями. Вони розглядаються пізніше.

На додаток до конкретних, змінним і параметрам, що представляють відповідно певну ознаку або базу, також розглядатимемо узагальнені змінні і параметри. Останні є абстрактними величинами, тобто величини, не визначені через які-небудь властивості або бази. Їх безліч станів і параметричні множини, а також різні відносини, визначені на цих множинах, представляються якимсь відповідним стандартним чином.

К.Р. № 3

Для деякої системи опишіть конкретні і узагальнені змінні і параметри.

Лекція 4

Канали спостереження

Назвемо каналом спостереження розуміємо будь-яку операцію, що вводить конкретну змінну як відображення (або конкретизацію) властивості.

Канал спостереження, за допомогою якого властивість ai представляється змінною, реалізується функцією

Oi : Ai→ 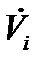, (1.6)

Ця функція гомоморфна щодо передбачуваної свойстві 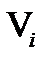безлічі Ai і .

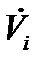Аналогічна функція, скажімо

ωj : Bj → 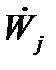, (1.7)

задає представлення бази bj, параметром 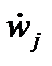, вона також повинна бути гомоморфной щодо відповідних властивостей бази (наприклад, часу) і множини ▲

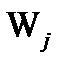Для деяких властивостей і баз канали спостереження можуть бути явно заданими функціями oi і ωj. Проте в інших випадках, коли множини А і В невідомі. При цьому представлення властивостей і баз вводяться фізично (операційно), а не за допомогою математичних визначень.

За винятком тривіальних випадків, коли функції oi і ωj, визначені ясно, канал спостереження є фізичним пристроєм і процедурою, що описує його застосування. Цей пристрій звичайно називається вимірювальним приладом або інструментом. Процедура є набором команд, що визначають те, як слід використовувати інструмент в різних умовах.

Будь-який вимірювальний інструмент повинен уміти взаємодіяти з вимірюваною властивістю і перетворювати цю взаємодію у вигляд, що безпосередньо представляє стани відповідної змінної (наприклад, свідчення покажчика на шкалі буквено-цифрового дисплея або просто запис значень).

Не дивлячись на те, що вимірювальні інструменти і процедури, створюючі канали спостереження, повинні відповідати деяким загальним принципам вимірювання, вони істотно залежать від того, що вони вимірюють. Тому їх вивченням, створенням і використанням займаються, головним чином, в рамках традиційних наукових дисциплін.

Канали спостереження враховуються в схемі АСНД тільки як компоненти, необхідні для повного визначення будь-якої реально існуючої системи. У АСНД вони достатньо часто не включаються.

Приклад 1.1. Для ілюстрації введених понять покладемо, що ai - це встановлений щорічний дохід платника податків деякої країни за останній рік, як повідомляється в його податковій декларації за цей рік. Тоді Ai - це всілякі суми грошей від нуля до максимально уявної суми, скажемо до 100000.00 одиниць. Ця множина звичайно, оскільки мінімальна грошова величина, що має ходіння, - 0.1 одиниці. Ми розуміємо також, що ця множина повністю (лінійно) впорядкована. Для обчислення прибуткового податку досить розглядати тільки діапазони оподатковуваного податком доходу, де кожному діапазону відповідає певний відсоток доходу, який слід виплатити як прибутковий податок. Для спрощення будемо цими діапазонами рахувати діапазони 0-4999.99, 5000.00 - 9999.99, .... 90000.00 -94999.99, 95000.00-100000.00 і хай безліччю станів 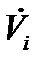, конкретної змінної, що представляє властивість ai, буде безліч мінімальних значень цих діапазонів. Змістовне представлення ai з допомогою можна ввести за допомогою функції ai, яка для кожного діапазону будь-якому значенню з діапазону привласнює мінімальне значення в цьому діапазоні, наприклад оi (52357) =50 000 або оi (796) =0. Очевидно, що функція оi гомоморфна щодо повного впорядкування Ai, оскільки для будь-якої пари

би, в Ai, якщо б в, оi(би) оi (в) . З методичних міркувань узагальнена змінна vi може бути для конкретної змінної визначена за допомогою абстрагуючої функції e-1i : m Vi . Ця функція повинна бути ізоморфною щодо впорядкування на . Припустимо, що потрібне, щоб безліч Vi була набором значень цілих чисел. Тоді e-1i можна, ймовірно, найбільш природним чином, задати наступним рівнянням:

e-1i (5000k)=k (k=0,1,., 19)

Базою в даному прикладі є безліч платників податків певної категорії, скажемо безліч жителів міста Х. Данноє множина не володіє ніякими математичними властивостями. Таким чином, ωj : Bj → 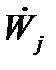може бути будь-який взаємно однозначною функцією, яка кожному платнику податків ставить у відповідність унікальний ідентифікатор. Методологічно зручно абстрагування ε-1j: 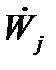→Wj представити у вигляді взаємно однозначної функції, що ставить у відповідність цілим числам

з безлічі Nn, де n - число платників податків в цій групі.

К.Р. № 4

Приведіть приклад систем з чіткими і нечіткими каналами спостереження, формалізуйте їх.

Лекція 5

Методологічні відмінності

Термін методологічна відмінність використовується тут для опису особливостей системних завдань, по яких розрізняються рівні типи завдань усередині одного типу моделей систем. Методологічні відмінності стосуються як систем, так і вимог до них.

Типи завдань, що відрізняються тільки деякими методологічними відмінностями, вимагають різних методів рішення, але мають один і той же статус в ієрархії типів моделей систем. Таким чином, методологічні відмінності є вторинними критеріями класифікації завдань наукових досліджень.

У даному розділі розглядаються методологічні відмінності, що відносяться до змінних і їх параметрів. Оскільки змінні і параметри є компонентами будь-якої системи незалежно від її типа, ці відмінності застосовні до систем всіх типів моделей.

Методологічні відмінності для змінних і параметрів - це характеристики їх безлічі станів і, відповідно, параметричних множин. Якщо змінна (або параметр) представляє властивість (або базу), то ці властивості не можуть бути довільними.

Всяка змінна пов'язана з одним або декількома параметрами, і зміни станів змінної спостерігаються на повній параметричній множині. Таким чином, комбінація властивостей безлічі станів і повної параметричної множини визначає самий елементарний тип методологічних відмінностей.

Якщо є більше одного параметра, то повна параметрична множина є декартовий твір окремих параметричних множин. Для представлення розпізнаваних властивостей цього декартова твори, властивості окремих параметрів повинні поєднуватися відповідним чином. Будемо спочатку для простоти вважати, що ми маємо справу з однією параметричною множиною незалежно від тієї, є воно окремою параметричною множиною або декартовим твором декількох, і що виділеними властивостями володіють вся ця множина.

Однією з фундаментальних методологічних відмінностей є відсутність математичних властивостей у безлічі станів або відповідної параметричної множини. Це крайній випадок, і він погано підходить для змінної (або параметра), що призначеної для представлення властивості (або бази) і має явно виражені і істотні для завдання характеристики. У літературі по вимірюваннях змінні такого роду звичайно називають змінними з номінальною шкалою.

Найбільш фундаментальною з властивостей безлічі станів і параметричних множин, що виділяються, є впорядкованість. Методологічно слід розрізняти два типу впорядкованості - часткову і лінійну.

Часткова впорядкованість - це бінарне відношення на множині (у нашому випадку на безлічі станів або параметричному), що є рефлексією, антисиметричною і транзитивною. Лінійна впорядкованість сильніше за часткову, оскільки це часткова впорядкованість, що володіє властивістю зв'язності (тобто будь-яка пара елементів множини так або інакше впорядкована).

Формально часткова впорядкованість Q, наприклад, безліч Vi - це бінарне відношення

Q 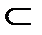Vi Vi ,(1.11)

що задовольняє наступним вимогам:

1. (x, x) Q (рефлексія);

2. якщо (x, y) Q і (y, x) Q, то х = у (антисиметричність);

3.якщо x, y) Q і (y, z) Q, то ( x, z ) Q (транзитивність).

Якщо (x , y) Q те х називається попередником у, а у - наступником х. Якщо (x , y) Q і не існує, z Q, такого, що ( x, z ) Q і (z, x) Q, то х називається безпосереднім попередником у, а у - безпосереднім наступником х. На додаток до вимог рефлексії, антисиметричності і транзитивності відношення лінійної впорядкованості задовольняє наступній вимозі зв'язності: для всіх х, y Vi, якщо 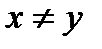, то або (x, y) Q або (y, x) Q. ▲

Прекрасним прикладом впорядкованості параметричної множини є час. Змінні з лінійно впорядкованою безліччю станів називаються змінними з впорядкованою шкалою.

Однією з найбільш істотних властивостей є відстань між парою елементів множини, що вивчається. Цей захід визначається функцією, що зіставляє будь-якій парі елементів цієї множини число, що визначає, на якій відстані один від одного знаходяться ці елементи з погляду деякого фундаментального впорядкування.

∆ Для даної множини, скажемо множини, відстань визначається функцією вигляду

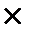
: →R , (1.12)

Однако для того, щоб ця функція відповідала інтуїтивному уявленню про відстань, вона повинна задовольняти наступним умовам для всіх х, у, z :

( 1) (x, y) 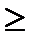0 (умова позитивності);

( 2) (x, y) = 0 тоді і тільки тоді, коли х = у (умова нульової відстані, звана також умовою невирожденності);

( 3) (x, y) = (y, x) (симетричність);

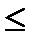
( 4) (x, y) (x, y) + (y, z) (нерівність трикутника).

Будь-яка функція, що задовольняє умовам ( 1) - ( 4), називається метричною відстанню на множині , а пара( , ) - метричним простором. Метрична відстань можна, зрозуміло, визначити як на безлічі станів, так і на параметричній множині. ▲

Прикладами змінних з вираженими і істотними метричними відстанями є майже всі змінні у фізиці, наприклад довжина, маса. Абсолютно очевидно, що і простір, і час - це параметри, до яких цілком природно застосовно поняття метричної відстані. Проте рідко вдається визначити метричну відстань на групах. Одним з таких прикладів є група студентів, лінійно впорядкована за показниками їх успішності. Змінні, з безліччю станів яких зв'язано метричну відстань, звичайно називаються метричними змінними.

Ще однією властивістю безлічі станів і параметричних множин, що має велике значення як методологічну відмінність, є безперервність. Це поняття добре відоме з математичного аналізу, і немає необхідності розглядати його тут детально.

Якнайкращим прикладом безперервного часткового впорядкування є відношення «менше або рівно», визначене на безлічі дійсних чисел або на його декартових творах. Фактично саме поняття безперервної змінної (або безперервного параметра) спирається на вимогу, щоб відповідна безліч станів (або параметрична множина) була ізоморфно безлічі дійсних чисел.

З цього виходить, що безліч станів будь-якої безперервної змінної або параметрична безліч будь-якого параметра нескінченно і незліченно. Тим самим альтернативою безперервним змінним і параметрам є змінні і параметри, задані на кінцевих множинах або, можливо, на нескінченних рахункових множинах. Останні називаються дискретними змінними або параметрами.

К.Р. № 5

Опишіть дві системи з різними методологічними відмінностями.

Лекція 6

2. Представляючі і початкові системи

К.Р. № 6

Опишіть формально деякі що представляє і результатну системи з вхідними і вихідними змінними.

Лекція 7

К.Р. № 7

Приведіть докладний приклад виродженої системи.

Лекція 8

3. Системи даних

Формалізація систем даних

Початкова система - це схема, по якій можуть бути зроблені спостереження відібраних ознак. Якщо канал спостереження чіткий, то будь-яке реальне спостереження представляється у вигляді впорядкованої пари, що складається із значення повного параметра, при якому було зроблене спостереження, і зафіксованого повного стану змінних.

У АСНД передбачається, що дані повинні бути представлені як узагальнені параметри і змінні. Отже, при формалізації поняття даних ми можемо обмежитися розглядом тільки узагальненої направляючої системи 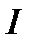, як вона визначена (2.11). Хай

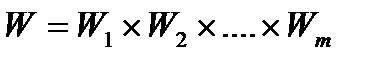(3.1)

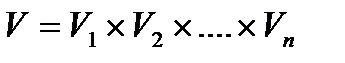(3.2)

Тоді чіткі дані представляються функцією

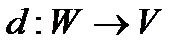(3.3)

Функція d будь-якому значенню повного параметра ставить у відповідність один повний стан змінних.

Представляюча система описує тільки потенційні стани змінних, тоді як функція d дає інформацію про їх дійсні стани при необмеженій параметричній множині. Тобто фактично відповідає досвідченим даним. Систему з функцією d можна розглядати як систему вищого типа (рівня 1). Називатимемо таку систему системою даних, і позначати D. Тоді

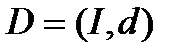(3.4)

Проте для будь-якого конкретного застосування у формулюванні повинен бути відображений і сенс даних d. Це можна зробити, замінивши представляючу систему в рівнянні (3.4) відповідною початковою системою S. Систему, що вийшла в результаті цієї заміни, назвемо системою даних з семантикою і позначимо SD. Таким чином

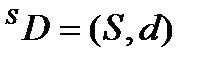(3.5)

В даному випадку функція d пов'язана з системою S таким чином: якщо спостереження, що описується з допомогою

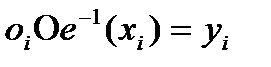
для всіх (де -предполагаемое прояв властивості, а - відповідний стан змінної ), зв'язується із значенням повного параметра, то

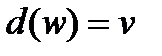(3.7)

де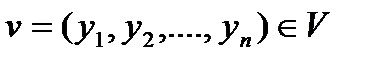

Залежно від даного завдання функція d може бути визначена трьома способами. По-перше, вона може бути результатом спостережень або вимірювань. По-друге, її можна вивести з систем вищих рівнів. По-третє, вона може бути визначена самим дослідником (у завданнях проектування систем).

Системи даних D і SD нейтральні. Перетворення цих систем в їх направлені аналоги і праці не представляє. Потрібно тільки замінити на, а S на .Таким образом

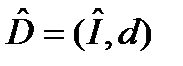(3.8)

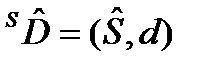(3.9)

- це направлені системи даних без представлення сенсу даних і з останнім відповідно.

Представлення даних

_ З яким типом даних - чітким або нечітким - ми маємо справу, завжди ясно по контексту. Чіткі дані можуть бути представлені в самому різному вигляді. Хай стандартною формою представлення дискретних змінних і параметрів буде матриця

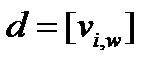(3.14)

елементами якої є стани змінних, наблюденниє при відповідних значеннях повного параметра w (мал. 3.1,а). Кожен стовпець матриці d задає повний стан, наблюденноє при даному w, а кожен рядок - всі спостереження однієї змінної на параметричній безлічі W. Якщо W лінійно впорядковане, то і стовпці в матриці d повинні бути впорядковані таким самим чином. Якщо використовуються декілька параметрів, то може опинитися зручніше використовувати інші форми уявлення.

Для нечітких даних стандартною формою уявлення, подібній матриці, є тривимірний масив 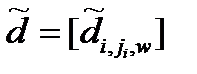(3.15)

елементами якого є значення ступеня упевненості в тому, що при заданому значенні параметра w спостерігався стан змінної 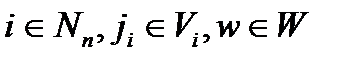, а 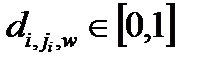. Масив є набором матриць (мал. 3.1,б), по одній для кожної змінної. Стовпець в матриці змінної задає функцію, визначувану рівнянням (3.10).

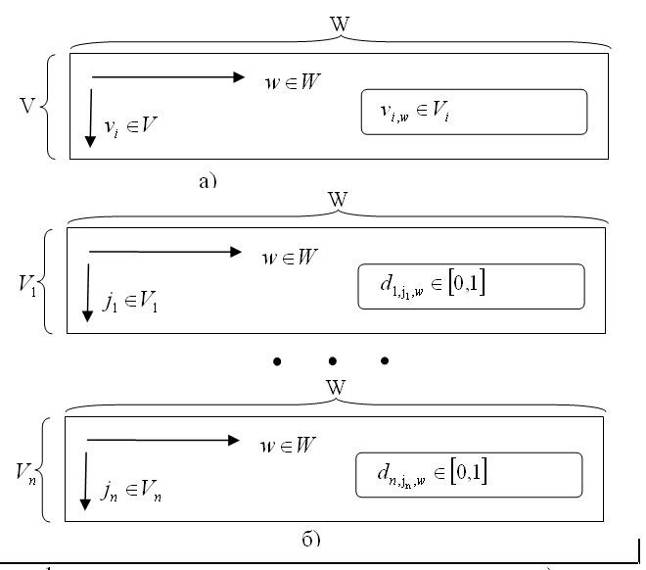
Рис. 3.1. Стандартне представлення данних для дискретних змінних. А) Чіткі дані. Б) Нечіткі дані.

К.Р. № 8

Опишіть формально деяку систему даних з нечіткими каналами спостереження.

Приведіть приклад представлення даних.

Лекція 9

4. Породжуючі системи

Системи з поведінкою

Термін поведінка використовується для характеристики загального параметрично інваріантного обмеження на змінні узагальненої представляючої системи і, можливо, на деякі додаткові абстрактні змінні. Додаткові змінні визначаються на параметричній множині за допомогою правил зрушення.

Оскільки опис параметрично інваріантного обмеження на дані змінні може бути використано для породження станів змінних при даній параметричній множині, системи, такі обмеження, що містять, називаються системами, що породжують. Поведінка є однією з форм завдання цього обмеження.

Для заданої узагальненої представляючої системи діапазон можливих типів параметрично інваріантних обмежень залежить від властивостей, що приписуються параметричній множині. Якщо на цій безлічі ніяких властивостей не визначено (як це часто буває для груп), то стани змінних можуть обмежувати тільки один одного. Проте якщо параметрична множина впорядкована, стани змінних можуть обмежуватися не тільки іншими станами, але і станами вибраного сусідства для кожного конкретного значення параметра.

Сусідство на впорядкованій параметричній множині звичайно називається маскою і визначається через змінні, параметричну множину і набір правил зрушення на параметричній множині. Правило зрушення, скажемо правило,- це однозначна функція

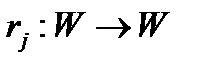(4.1)

яка кожному елементу W ставить у відповідність інший (причому єдиний) елемент W. Якщо, наприклад, параметрична множина повністю впорядкована (як у випадках, коли розглядається час або одночасний простір) і є безліччю послідовних цілих позитивних чисел, то будь-яке правило зрушення може бути задано простим рівнянням

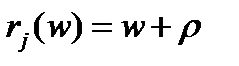(4.2)

де - ціла константа (позитивна, негативна або нуль). При називається тотожним правилом зрушення.

Все вище сказане, можна пояснити таким чином. Для того, щоб система, була здатна генерувати дані, з початкових даних, потрібно визначити деякі правила по яких виходитимуть нові дані. У вузькому сенсі це будуть деякі функції. Наприклад, лінійна функція однієї змінної - геометрично пряма. Ця функція перетворить значення аргументу, в деяке значення. У ширшому сенсі це параметрично інваріантне обмеження.

Вибіркові змінні і маски

Хай задана узагальнена представляюча система I, визначувана рівнянням (2.12). Позначимо через V безліч змінних з I, а через R набір правил зрушення, що розглядаються для цих змінних. Тоді безліч змінних

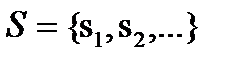(4.3)

званих вибірковими змінними, може бути введено за допомогою рівнянь

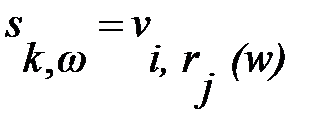(4.4)

для деяких змінних і правил зрушення ; позначає стан вибіркової змінної при значенні параметра w, а - стан змінної при значенні параметра, тобто при значенні, одержаному для заданого w, при застосуванні правила зрушення . Для повністю впорядкованої параметричної множини, правила зрушення якого мають вигляд (4.2), рівняння (4.4) може бути переписано в певнішому вигляді

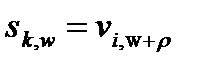(4.5)

Оскільки будь-яке правило зрушення з набору R може бути застосовано до будь-якої змінної з множини V, та безліч всіх можливих вибіркових змінних представляється декартовим твором . Насправді розглядаються вибіркові змінні, що характеризуються відношенням

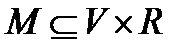(4.6)

так, що всякій парі відповідає одне рівняння з (4.4). Відношення М представляє схему сусідства на параметричній множині, в термінах якої визначені вибіркові змінні. Ця схема звичайно називається маскою.

Для введення ідентифікаторів вибіркових змінних до повинна бути введена якась однозначна функція (кодування).

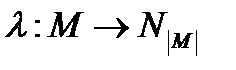(4.7)

де - це кількість елементів множини М.

Якщо вибіркова змінна визначена через змінну і деяке правило зрушення згідно рівнянню (4.4), то безліч станів, очевидно, То ж саме, що і безліч станів тобто . Проте для зручності позначень безліч станів вибіркової змінної позначатимемо ; сенс будь-якого 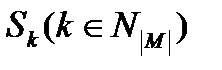однозначно визначається маскою в термінах однієї з множин 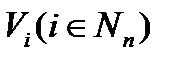. Таким чином, декартовий твір 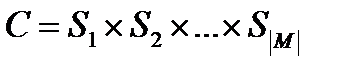(4.8)

є повною безліччю станів вибіркових змінних.

К.Р. № 9

Опишіть систему з поведінкою у разі повністю впорядкованих параметричних множин. (Обов'язково необхідно вказати маски і вибіркові змінні.)

Лекція 10

4.4 Функції поведінки. Змінні, що породжують і породжувані.

Найпростіший спосіб завдання певної маски - це перелік всіх повних станів відповідних вибіркових змінних. У загальному вигляді подібний перелік є підмножиною декартова твори З, тобто багатовимірним відношенням, визначеним на С. Это відношення визначається функцією

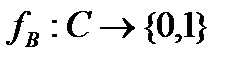
такий, що, якщо стан з входить в перелік, і інакше. Така функція дає деякі відомості про поведінку вибіркових змінних, функцію звичайно називають функцією поведінки. Функція, визначувана рівнянням (4.11), задає тільки одного з існуючих типів функцій поведінки, що різними способами описують обмеження на змінні.

Функція визначає стани, що зустрічаються, з, але не визначає значення параметра, при якому вони мають місце. Таким чином, ця функція є параметрично інваріантною.

Система, що характеризує параметрично інваріантне обмеження на безліч змінних через функції поведінки, визначається трійкою

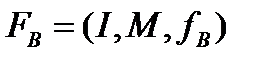(4.12)

де I - узагальнена представляюча система; М - маска, визначена на I; -функция поведінки, визначена через М і I. Таку систему називатимемо системою з поведінкою

Не дивлячись на те, що будь-яка система з поведінкою, визначувана (4.12), якимсь конкретним параметричні інваріантно описує обмеження на змінні представляючої системи, вона не містить опису того, як використовувати це обмеження для породження даних. Для розробки такого опису потрібно розбити вибіркові змінні на дві підмножини:

1) змінні, стани яких породжуються з обмеження; назвемо їх породжуваними змінними;

2) змінні, стани яких використовуються як умови в процесі генерації, назвемо їх змінними, що породжують.

Для заданої системи з поведінкою одним із способів визначення породжених змінних, що породжують, є визначення для даної маски М двох підмасок і . Будемо

(4.13)

Де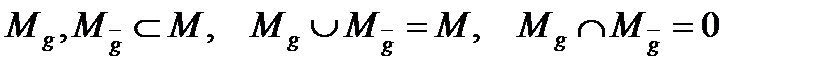

називати маскою породження, тобто це маска М і її розбиття на породжувану підмаску і що породжує підмаску .

По аналогії з розбиттям на і безліч ідентифікаторів вибіркових змінних можна розбити на дві підмножини, скажемо і, що представляють ідентифікатори відповідно породжуваних змінних, що породжують. Для зручності позначень кодуюча функція (4.7) може бути замінена двома функціями

(4.15)

за допомогою яких безліч станів і відповідно породжуваних змінних, що породжують, задаються декартовими творами

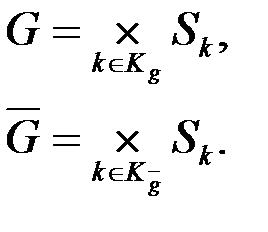(4.16)

Тепер спосіб представлення стану породжуваних змінних (скажімо ), визначуваного за станом змінних (скажімо ), що породжують, можна виразити функцією

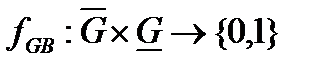(4.17)

де

(4.18)

Назвемо цю функцію функцією поведінки, що породжує.

Якщо маску М і функцію з (4.11) замінити відповідно на і функцію, то вийде альтернативна система

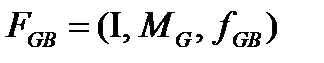. (4.19)

Називатимемо таку систему системою, що породжує, з поведінкою.

Використання системи, що породжує, з поведінкою для породження даних включає наступні два етапи:

а) для деякого значення задано стан ; для визначення стану при тому ж значенні використовується функція ;

б) значення t замінюється на нове і повторюється етап а).

К.Р. № 10

Для деякої системи з поведінкою, опишіть функції поведінки. Приведіть приклад процедури породження даних.

Лекція 11

К.Р. № 11

Опишіть функції поведінки для недетермінованих направлених систем.

Лекція 12

Особливості побудови масок

Якщо дана маска є одним стовпцем (маска без пам'яті), то вибірки по всіх значеннях параметра є повними. Проте, якщо маска полягає із понад одного стовпця, то деякі вибірки на початку і кінці параметричної множини (лівий і правий краї матриці даних) виявляться неповними (див. мал. 4.2 і 4.3). Точніше, число неповних вибірок для кожного краю матриці даних рівне числу стовпців в масці мінус 1. Число стовпців в масці М називатимемо завглибшки маски і позначати . Тоді

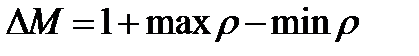(4.34)

де оператори max і min застосовані до всіх цілих 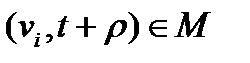. Так, наприклад, для маски, визначеної на мал. 4.1,, для масок без пам'яті .

Є два міркування, по яких застосування масок з великою глибиною в загальному випадку небажано.

1. якщо маска використовується для породження даних, то чим більша її глибина, тим більше потрібна початкова умова. Це, взагалі кажучи, не бажано.

2. якщо маска використовується для вибірки даних, то число неповних вибірок рівне . Це означає, що із зростанням глибини маски все менше наявних даних використовується для визначення функції поведінки. Отже, із збільшенням глибини маски звужується емпірична основа, на якій будується функція поведінки. Це, зрозуміло, також небажано.

Обидва ці міркування, а також практичні міркування, пов'язані з складністю обчислень, призводять до того, що глибина маски звичайно вибирається не дуже великою. Таким чином, представляється доцільним визначити обмеженість глибини маски як вимогу 1 для даного типа завдань. Це можна зробити, визначивши найбільшу допустиму маску, скажемо маску М як декартовий твір

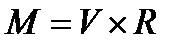(4.35)

де .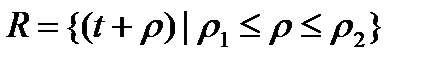

Подібна маска може бути представлена у вигляді повної матриці з п рядками і 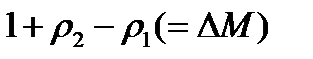стовпцями. Називатимемо її М-матрицею. Якщо спочатку задано тільки, але не конкретні значення і, то доцільно вибирати для них якісь стандартні значення, наприклад, 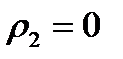,а .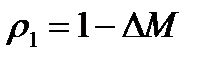

Змістовні підмаски

При заданій найбільшій допустимій масці М всі її змістовні підмаски утворюють обмежену безліч Yr систем з поведінкою. Термін «змістовна підмаска» характеризує підмаски М, що задовольняють наступним вимогам:

(ml) у підмаску входить принаймні один елемент з кожної підмаски, визначеної рівнянням (4.10) (тобто один елемент з кожного рядка М-матриці);

(m2) у підмаску повинен бути включений принаймні один елемент з правилом зрушення (крайній правий елемент з М-маски).

Вимога ml необхідна для покриття заданої системи даних, тобто для того, щоб гарантувати, що будь-яка базова змінна із заданої системи даних була б включена в будь-яку з систем з поведінкою з обмеженої безлічі Yr. Вимога m2 перешкоджає дублюванню еквівалентних підмасок, тобто підмасок, що перетворюються одна в іншу тільки за допомогою додавання константи до правила зрушення (зрушення ряду в М-масці).

Можна легко одержати формулу для числа 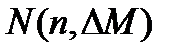змістовних підмасок найбільшої допустимої маски, де n - число базових змінних, а - глибина маски М:

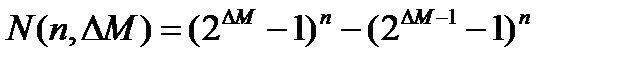. (4.36)

Перший член виразу (4.36) задає число підмасок М, що задовольняють умові ml, а другий член - число масок, що порушують умову m2. У табл. 4.1 приведені значення при п .

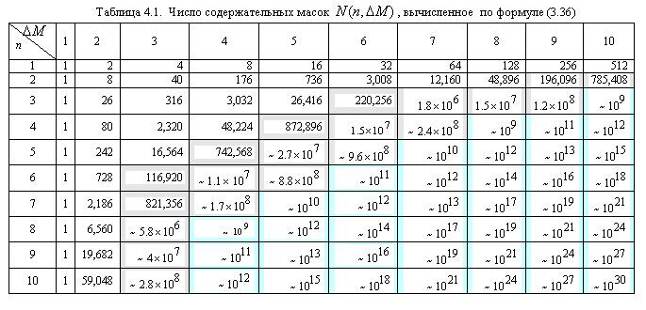
Ця таблиця розділена на три області, для яких розміри найбільшої допустимої маски представляються: а) що легко піддаються обчислювальній обробці (ліва верхня область); би) що у принципі піддаються обробці, що зажадає тривалої роботи дуже могутнього комп'ютера (середня область); у) що не піддаються обчислювальній обробці (права нижня область). Ці області показані тільки для найбільш типового випадку. Так, наприклад, якщо є в розпорядженні могутня система паралельних обчислень, то область випадків, що піддаються обчислювальній обробці, може бути розширена майже удвічі.

Якщо число змістовних масок виявляється дуже велике, щоб піддаватися обчислювальній обробці, АСНД повинні враховувати можливі додаткові обмеження, що накладаються на найбільшу допустиму маску. Такими обмеженнями можуть бути, наприклад, наступні:

1. фіксація безлічі породжуваних вибіркових змінних;

2. фіксація числа вибіркових змінних;

3. фіксація верхньої межі числа вибіркових змінних;

4. обмеження, при якому розглядаються талько маски без пропусків (прикладом пропуску є елемент, що ідентифікується координатами, в масці, зображеній на мал. 4.1,а).

Подібні обмеження або їх комбінації істотно скорочують множину, і таким чином, збільшують розмір найбільших допустимих масок, що піддаються обчислювальній обробці.

К.Р. № 12

Виходячи з деякої системи даних, побудувати функцію поведінки, у разі масок без пам'яті.

Лекція 13

Заходи нечіткості

Ступінь недетермінованої повинен вимірюватися узагальненою нечіткістю, супутньою породженню даних. А значить, вона повинна бути визначена через функції поведінки, що породжують, і для нейтральних і направлених систем з поведінкою. Якщо ці функції є функціями розподілу вірогідності, то міра узагальненої нечіткості добре відома - це шенноновськая ентропія

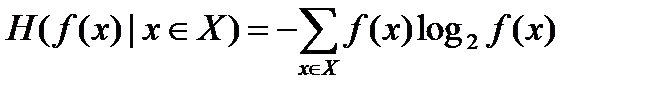
Вона вимірює нечіткість в одиницях, званих бітами.

Якщо припустити, що будь-яка кінцева множина X дані альтернативні вихідні значень характеризується певним розподілом вірогідності, то зручніше спростити позначення і писати замість .

Легко бачити, що

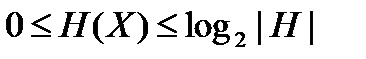(4.38)

Нижня межа досягається у тому випадку, коли вірогідність всіх вихідних значень, за винятком одного, рівна 0; верхня межа досягається тоді, коли вірогідність всіх подій однакова, тобто рівні . Відношення ентропії до її верхньої межі

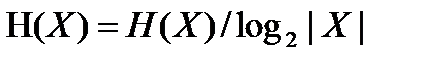(4.39)

називається нормалізованою ентропією; зрозуміло, що

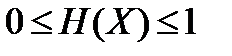(4.40)

У нашому випадку безліччю виходів є множини а розподіли вірогідності представляються функціями поведінки, визначуваними відповідно формулами (4.11) (4.17) (4.27) (4.30). Для спрощення запису опустимо індекси В і GB, а також знак ^ . Таким чином

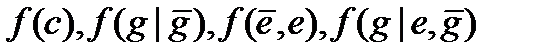(4.41)

позначає вірогідність, визначувана відповідно формулами (4.11) (4.17) (4.27) (4.30); сенс будь-якого з цих позначень однозначно визначається укладеними в дужки аргументами. Крім того, визначимо безумовну вірогідність

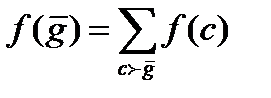(4.42)

де указує на те, що є підмножиною стану з (підстаном з); формально, якщо

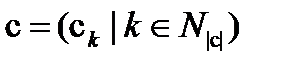(4.43)

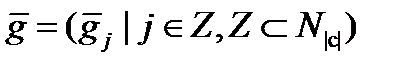(4.44)

то тоді і тільки тоді, коли для всіх . Для направлених систем безумовна вірогідність обчислюється по небагато зміненій формулі

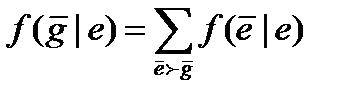(4.45)

Умовна вірогідність, що характеризує процес породження даних, пов'язана з основною (сумісними) і безумовною вірогідністю таким чином:

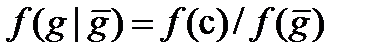(4.46)

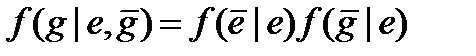. (4.47)

Перша формула описує цей зв'язок для нейтральних, а друга - для направлених систем.

Методи обчислень нечіткості

При заданій масці, що породжує, для нейтральної системи, через яку визначається безліч станів вибіркових змінних, що генеруються і генеруючих, нечіткість, що породжує, визначається як середня нечіткість, що базується на вірогідності, зважених вірогідністю умов, що породжують:

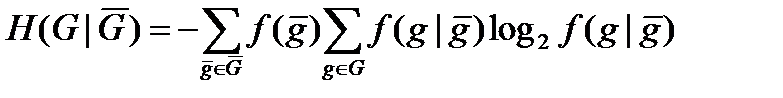. (4.48)

Це значення визначає ступінь недетермінованої системи, що даної нейтральної породжує, з поведінкою.

Для направлених систем нечіткість, що породжує, обчислюється за формулою

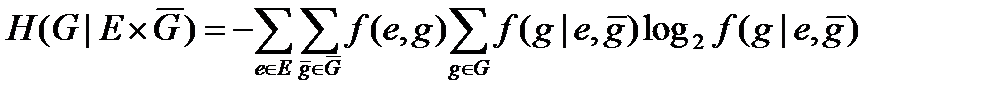(4.49)

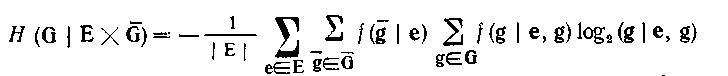
яку можна безпосередньо застосовувати у тому випадку, коли можна і має сенс визначати вірогідність, тобто коли направлена система одержана з нейтральної. Якщо ми не маємо в своєму розпорядженні вірогідності станів елементів безлічі Е або ця вірогідність неістотні, тоді як базова вірогідність береться вірогідність [аналог вірогідності f(c) для нейтральних систем], виходячи з якої обчислюється решта необхідної вірогідності. В цьому випадку нечіткість обчислюється формулі (4.50)

де вірогідність і обчислюються по заданій вірогідності згідно формулам (4.45) і (4.47).

Формули (4.48), (4.49) і (4.50) можна замінити іншими, зручнішими для обчислення. Наприклад, рівняння (4.48) можна модифікувати таким чином:

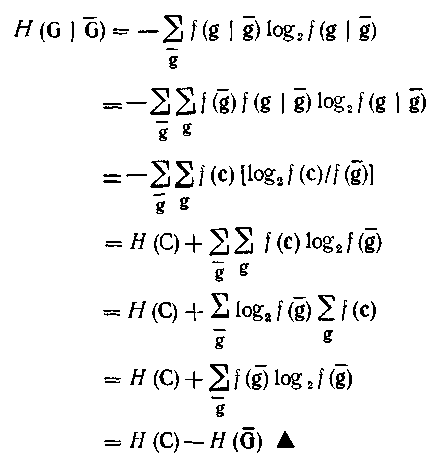
Таким чином, можна обчислити, не використовуючи умовну вірогідність, по формулі

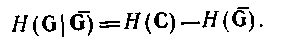(4.52)

Так само рівняння (3.49) і (3.50) можна замінити відповідно рівняннями

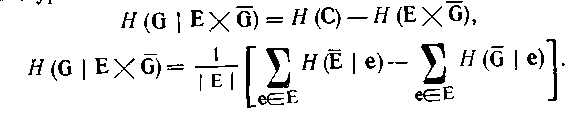(4.53)

Максимальне значення нечіткості будь-якого типа, що породжує, рівне; отже, нормалізована нечіткість, що породжує, виходить діленням нечіткості, що породжує, на її максимальне значення. Наприклад

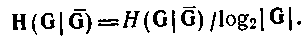
Приклад 4.2. На мал. 4.5,а показана імовірнісна функція поведінки для чотирьох вибіркових змінних кожна з двома станами - 0 і 1. Стани з нульовою вірогідністю в таблиці не приводяться. Вибіркові змінні визначені через дві базові змінні за допомогою маски, зображеної на мал. 3.7,а. Оскільки вибіркові змінні суть зрушення однієї і тієї ж базової змінної, розподіли вірогідності їх станів повинні бути однакові; вони і справді однакові; обидва мають вірогідність 0.7 і 0.3 відповідно для станів 0 і 1. Аналогічно змінні (зрушення) мають однаковий розподіл вірогідності: 0.6 і 0,4 відповідно для станів 0 і 1. Отже, для даної маски приведена функція розподілу вірогідності є коректною функцією поведінки.

Якщо дана система інтерпретується як нейтральна, її нечіткість, що породжує, може бути обчислена за формулою (4.52). Для першого члена формули ми маємо

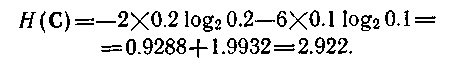
Значення другого члена залежить від порядку породження і від відповідної маски. На мал. 4.5,в і г показані два можливі порядки породження. Для породження зліва направо маємо

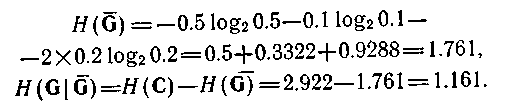
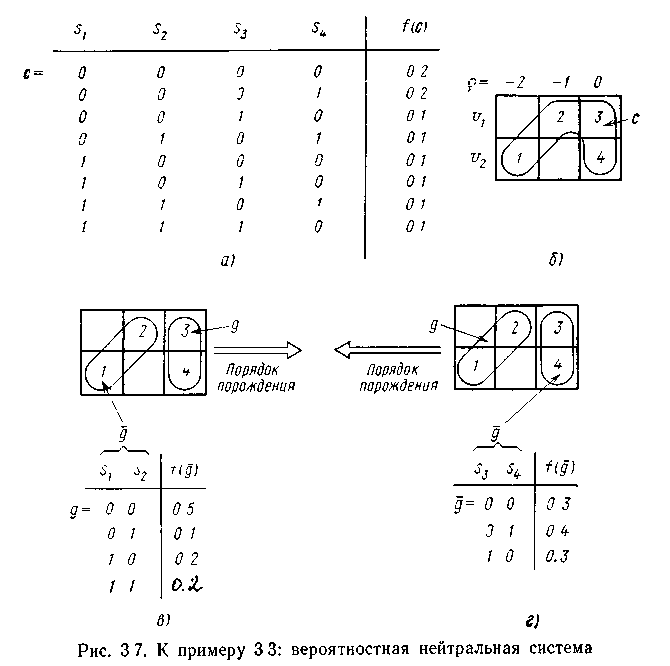
Мал. 4.5 Імовірнісна нейтральна система

Для іншого порядку породження (мал. 4.5,г) ми одержимо

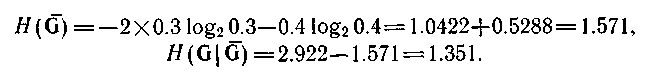
Отже, нам можна вибрати один з двох порядків породження; перший порядок переважно, оскільки має нижчу породжувану нечіткість. Оскільки в даному прикладі, то нормалізовані значення тих, що обчислювальних породжують нечеткостей виходять діленням їх на два.

В деяких випадках застосуємо тільки один порядок породження. Якщо, наприклад, параметром є час, то у кожному випадку має сенс тільки один з порядків, визначуваний метою використання системи з поведінкою. Якщо вона використовується для прогнозу, то стани повинні породжуватися у порядку зростання часу (зліва направо); якщо ж вона використовується для ретроспекциі, то стани повинні породжуватися у порядку убування часу. У даному прикладі, якщо параметром є час, то виявляється легшим передбачати майбутні стани системи, чим визначати минулі.

Припустимо тепер, що інтерпретується як вхідна змінна і що по функції поведінки на мал. 4.5,а визначена відповідна направлена система. Тепер для обчислення нечіткості, що породжує, можна скористатися формулою (4.53). Нечіткість вже була обчислена раніше;зависит від порядку породження. У будь-якому випадку безліч Е представляється станами переменнихпредставляєтся або станами (у порядку зростання параметра) або станами (у порядку убування параметра). У першому випадку нечеткостьсвязана із змінними

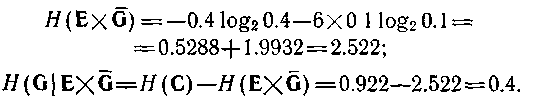
У другому випадку вона представляє нечіткість змінних:

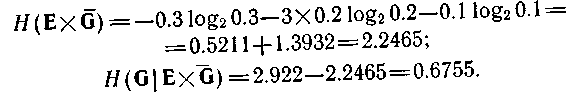
Таким чином, знову виявляється, що передбачати майбутні стани легше, ніж визначати минулі.

Припустимо тепер, що ми не маємо в своєму розпорядженні ніякої інформації щодо вхідної змінної або що ця інформація неістотна (наприклад, у тому випадку, коли контролюється користувачем). Тоді всі обчислення повинні проводитися для приведеної на мал. 4.6,а умовної вірогідності. Як показано на цьому малюнку, список вірогідності разбітна чотири частини, відповідні різним станам е. Нечіткості для кожного стану також приведені на мал. 4.6,а. Тут же показано розбиття маски на

Ситуація при породженні станів зліва направо, включаючи значення для кожного стану е, показана на мал. 4.6,в.

З формули (4.53) одержимо

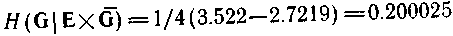
Інший порядок породження зображений на мал. 4.8,г. Для нього маємо

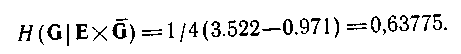
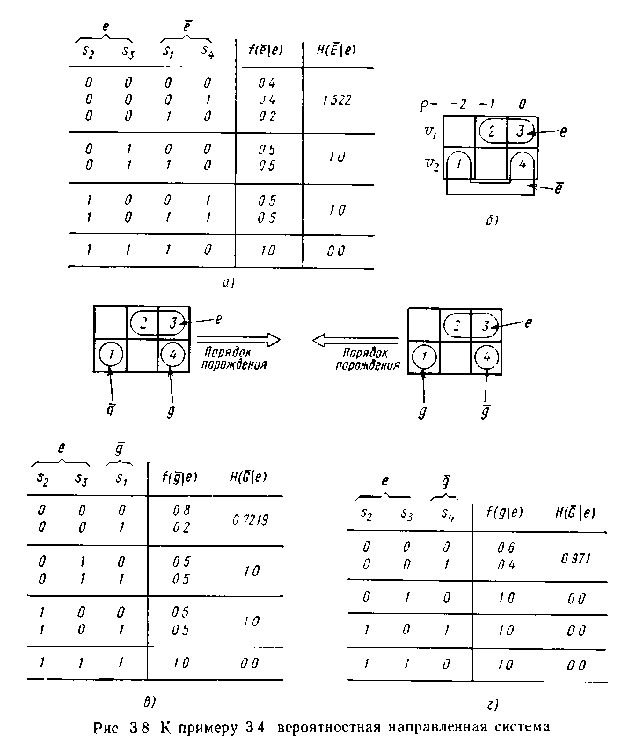
Мал. 4.6 Імовірнісна направлена система

К.Р. № 13

Розрахувати ту, що породжує нечіткість для випадку направленої і нейтральної системи з поведінкою. Розглянути обидва порядки породження.

Лекція 14

К.Р. № 14

Для деякої системи даних упорядкувати маски по складності і нечіткості.

Лекція 15

К.Р. № 15

Опишіть ST-функцію для системи із станами, що змінюються.

Лекція 16

К.Р. № 16

Приведіть приклад переходу від деякої ST-системи до ізоморфоной системи з поведінкою.

Лекція 17

Види систем, що породжують

системи з поведінкою

1. базовиє-

а. рівняння (4.12) -нейтральные;

b. рівняння (4.28) -направленные;

2. що породжують:

а. рівняння (4.19) -нейтральные;

b. рівняння (4.32) -направленные;

ST-системи

1. базові:

а. рівняння (4.66) -нейтральные

b. рівняння (3.93) -направленные;

2. що породжують:

а. рівняння (4.86) - нейтральні;

b. рівняння (4.87) -направленные.

Як було показано, будь-яка ST-система може бути перетворена в ізоморфну систему з поведінкою, тоді як зворотне перетворення можливо тільки при певному типі масок. Отже, системи з поведінкою більш загальні, ніж ST-системи.

Два основні недоліки ST-систем очевидні: обмеженість із-за використання тільки компактних масок і власна надмірність, що виникає з накладення поточного і наступного станів.

ST-системи, коли вони застосовні, представляють для дослідників певні переваги. Мабуть, ST-функції зрозуміліше людині, чим аналогічні функції поведінки.

Для систем, що породжують, виділені різні відмінності. Це відмінності, виділені для систем нижчих рівнів, і деякі нові. Серед перших найбільш істотними є:

1. впорядкованість параметричної множини, що дозволяє ввести важливе поняття маски;

2. впорядкованість безлічі станів, що грає істотну роль в спрощенні процедур для систем, що породжують, і при роботі з не повністю певними наборами даних;

3. відмінність чітких і нечітких каналів спостереження, що дають відповідно чіткі або нечіткі дані і вимагаючих застосування різних методів обробки даних;

4. відмінність між нейтральними і направленими системами, з якими слід поводитися по-різному.

Відмінностями, що відносяться до систем, що породжують, але не до систем даних і початкових систем, є:

1. детермінована і недетермінована систем;

2. по використовуваній масці розрізняються системи без пам'яті і системи, що породжують, залежні від минулого.

Зрозуміло, ці методологічні відмінності характеризують і системи вищих рівнів.

К.Р. № 17

Для деякої системи, що породжує, приведіть приклади можливих спрощень.

Лекція 18

Дослідження і проектування за допомогою АСНД

В цілому АСНД призначені для вирішення завдань наступних двох типів. Завданням дослідження систем є накопичення знань про різні набори змінних і параметрів, визначених з конкретною метою на існуючих об'єктах. Завданням проектування систем є використання накопичених знань для створення нових об'єктів, для яких на певні змінні накладені відомі обмеження. Вся розглянута вище теорія формалізує і надає можливі шляхи створення АСНД загального вигляду для довільної наочної області.

Існує два основні підходи використання АСНД. При одному системи (або системи вищих рівнів), що відповідні породжують, базуються на певних вимогах, виводяться із заданої системи даних. Цей підхід звичайно називається методом відкриття.

При іншому підході гіпотетична система (або система вищого рівня) постуліруєтся, що породжує, а потім її правильність перевіряється порівнянням породжуваних нею (за відповідних початкових умов) даних з емпіричними даними. Якщо система не проходить перевірки, заснованої на конкретному критерії правильності (критерії збігу), то вона відкидається і постуліруєтся нова система. Цей підхід до дослідження систем звичайно називається методом того, що постулювало.

При використанні методу відкриття будь-яка система, що породжує, одержана безпосередньо з системи даних, є якимсь економним представленням якихось аспектів системи даних. Те, які саме аспекти представляються системою, що породжує, залежить від її маски і характеру функції поведінки або ST-функції. Якщо система, що породжує, детермінована, то цей економний опис всієї системи даних свого роду «стенографічний» опис.

Таким чином, проектування систем в запропонованому варіанті АСНД завжди є процесом підйому за ієрархією систем. Він починається з визначення або що породжує системи, або системи даних і набору вимог щодо структури систем. Дослідження за допомогою АСНД здійснюється з допомогою:

1. підйому за ієрархією за допомогою виявлення систем вищих рівнів, для яких системи нижчих рівнів володіють певними властивостями (метод відкриття);

2. постулювали систем, що породжують, або систем вищого рівня і відкидання тих з них, які не задовольняють перевірці на відповідність між емпіричними і породженими даними (метод того, що постулювало);

3. будь-якої комбінації методу відкриття і методу того, що постулювало, наприклад підйому за ієрархією до певного рівня і постулювало систем на більш високому рівні.

АСНД - конспект лекцій

Лекція 1

Введення 2

Завдання наукових досліджень 2

Систем і їх типи 3

1. Загальні поняття і визначення

Лекція 2

1.1 Об'єкти і системи об'єктів 4

1.2 Базові властивості 5

1.3 Обмеження на вибір баз 5

1.4 Формальне визначення системи 6

Лекція 3

1.5 Змінні і параметри 6

1.6 Узагальнені змінні і параметри. Формалізація. 7

Лекція 4

1.7 Канали спостереження 8

1.8 Нечіткі канали спостереження 9

Лекція 5

1.9 Методологічні відмінності 11

1.10 Методологічні відмінності на рівні змінних і параметрів 13

2. Представляючі і початкові системи

Лекція 6

2.1 Формалізація представляючих і початкових систем 14

2.2 Системи з вхідними і вихідними змінними 16

Лекція 7

2.3 Вироджені типи направлених систем 17

3. Системи даних

Лекція 8

3.1 Формалізація систем даних 21

3.2 Системи даних з нечіткими каналами спостереження 22

3.3 Представлення даних 22

4. Породжуючі системи

Лекція 9

4.1 Системи з поведінкою 23

4.2 Вибіркові змінні і маски 24

4.3 Маски у разі повністю впорядкованих параметричних множин 25

Лекція 10

4.4 Функції поведінки. Змінні, що породжують і породжувані. 26

4.5 Особливості процедури породження даних 27

Лекція 11

4.6 Функції породження для недетермінованих систем 30

4.7 Направлені системи з поведінкою 31

Лекція 12

4.8 Перехід від систем даних, до систем з поведінкою 32

4.9 Особливості переходів, залежно від властивостей параметричної множини 33

4.10 Особливості побудови масок 34

4.11 Змістовні підмаски 34

Лекція 13

4.12 Заходи нечіткості 35

4.13 Методи обчислень нечіткості 36

Лекція 14

4.14 Вибір відповідних систем з поведінкою 40

4.15 Впорядкування по складності і нечіткості 41

Лекція 15

4.16 Системи із станами, що змінюються 45

Лекція 16

4.17 Взаємозв'язок ST-систем і систем з поведінкою 49

Лекція 17

4.18 Види систем, що породжують 52

4.19 Спрощення систем, що породжують 53

Лекція 18

Дослідження і проектування за допомогою АСНД 56

Лекція 1

Введення

Завдання наукових досліджень

Предметом завдань наукових досліджень в прикладному сенсі є системи. Оскільки поняття системи охоплює всі об'єкти матеріального світу.

Таким чином, класифікація завдань наукових досліджень може бути визначена відповідно до класифікації систем. Як відомо, система в загальному випадку є впорядкованою парою, де - A безліч елементів системи, а R- безліч відносин між ними. Тепер вводячи певні класи впорядкованих пар можна виділити деякі класи завдань наукових досліджень. Вказані класи можна ввести за наступними ознаками:

а) виділення завдань, в яких розглядаються певні типи елементів систем;

б) виділення завдань, в яких розглядаються певні типи відносин між елементами систем.

Завдання, що розрізняються за ознакою а), детально розглядаються в різних прикладних курсах. Тут нас цікавить класифікація переважно за ознакою. б). Оскільки саме цей шлях дозволяє автоматизувати системи наукових досліджень, в найбільш загальному сенсі. Тобто створити АСНД, які можна застосовувати до будь-яких областей людської діяльності, у тому числі і до завдань гнучких роботизованих систем.

У принципі безліч всіляких завдань наукових досліджень є нескінченною, але такою, що зводиться до кінцевого числа добре певних типів завдань. Що означає, можливість розробки методів рішення того або іншого типу завдань. У загальному випадку схема роботи АСНД може бути представлена таким чином (мал. 1).

На схемі видно два альтернативні процеси - абстрагування і інтерпретації, які пов'язують АСНД із зовнішнім світом, тобто конкретною наочною областю. Абстрагування, означає формування моделі досліджуваного об'єкту, використовуючи поняття характерні для . Інтерпретація, означає трактування отриманих результатів, використовуючи поняття характерні для досліджуваного об'єкту. Підкреслимо, що ця схема є загальною схемою для наукових досліджень будь-якого характеру.

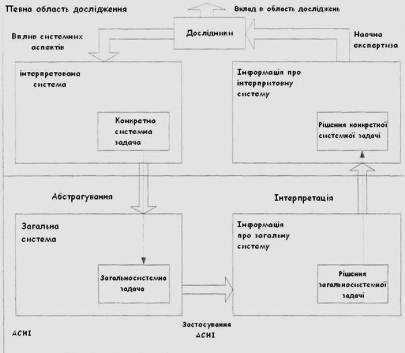
Рис.1 Загальна схема роботи АСНД

Систем і їх типи

Рис.2 Ієрархічна схема типів систем

К.Р. № 1

Охарактеризуйте загальну схему роботи АСНД, і ієрархічні типи систем.

Лекція 2

1. Загальні поняття і визначення

Об'єкти і системи об'єктів

Згідно цьому визначенню об'єкти можуть бути як

а) матеріальними, так і

б) абстрактними.

Базові властивості

Обмеження на вибір баз

Дата: 2019-03-05, просмотров: 273.

12 3 4 5 6 7 8 9 10 Следующая ⇒