На додаток до конкретних, змінним і параметрам, що представляють відповідно певну ознаку або базу, також розглядатимемо узагальнені змінні і параметри. Останні є абстрактними величинами, тобто величини, не визначені через які-небудь властивості або бази. Їх безліч станів і параметричні множини, а також різні відносини, визначені на цих множинах, представляються якимсь відповідним стандартним чином.

 Введення узагальнених змінних, в основному, обумовлене поліпшенням представлення деяких даних. Наприклад, хай деяка змінна визначена на безлічі цілих чисел. Тоді деяким інтервалам цілих чисел, можуть бути поставлені у відповідність деякі якісні характеристики. Останні і представлятимуть узагальнені змінні. Сенс узагальнених змінних уточнюється нижче.

Узагальненій змінній дається інтерпретація, коли безліч її станів відображається ізоморфно (тобто відображається взаэмнооднозначно один до одного із збереженням всіх істотних математичних відносин, визначених на ньому) в елементи безлічі станів конкретної змінної; те ж відноситься до узагальнених і конкретних параметрів і їх параметричних множин. Будь-яке ізоморфне відображення такого роду називатимемо конкретизацією узагальненої змінної (або узагальненого параметра), а зворотне відображення назвемо абстрагуванням конкретної змінної (або конкретного параметра).

Для формалізації понять узагальнених і конкретних змінних і їх параметрів введемо наступні позначення на додаток до введених в попередньому розділі.

 vi, Vi, 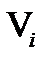 - що означають відповідно узагальнену змінну, її безліч станів і безліч математичних властивостей, визначених для неї;

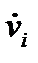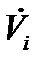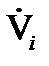, , - ті ж характеристики конкретної змінної, що є конкретизацією змінної vi;

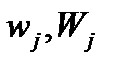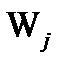 і  -відповідно узагальнений параметр, його безліч станів і безліч математичних властивостей, визначених на параметрі wj;

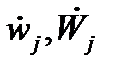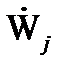і - ті ж характеристики конкретного параметра, одержані конкретизацією параметра wj.

АСНД працює, в основному, тільки з узагальненими змінними і параметрами. Задана узагальнена змінна vi, конкретизується змінній 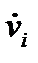 тоді і тільки тоді, коли функція

ei : Vi→ 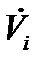,(1.2)

існує і ізоморфна щодо математичних властивостей 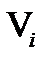 . Аналогічно узагальнений параметр wj конкретизується параметром  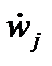тоді і тільки тоді, коли функція

εj : Wj → 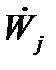, (1.3)

існує і ізоморфна відносно  .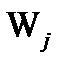

Кожен конкретний ізоморфізм ei (або εj) задає конкретизацію vi з допомогою 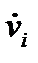 (або відповідно wj з допомогою ).

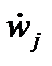Функції, зворотні ei і εj,, тобто

e-1i : 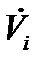→ Vi ,(1.4)

ε-1 j : 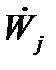→ ,(1.5)

задають абстрагування відповідно 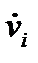 і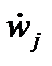

К.Р. № 3

Для деякої системи опишіть конкретні і узагальнені змінні і параметри.

Лекція 4

Канали спостереження

 Назвемо каналом спостереження розуміємо будь-яку операцію, що вводить конкретну змінну як відображення (або конкретизацію) властивості.

 Канал спостереження, за допомогою якого властивість ai представляється змінною, реалізується функцією

Oi : Ai→ 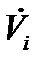, (1.6)

Ця функція гомоморфна щодо передбачуваної свойстві 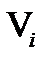безлічі Ai і .

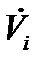Аналогічна функція, скажімо

ωj : Bj → 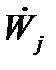, (1.7)

задає представлення бази bj, параметром 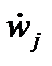, вона також повинна бути гомоморфной щодо відповідних властивостей бази (наприклад, часу) і множини ▲

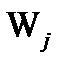Для деяких властивостей і баз канали спостереження можуть бути явно заданими функціями oi і ωj. Проте в інших випадках, коли множини А і В невідомі. При цьому представлення властивостей і баз вводяться фізично (операційно), а не за допомогою математичних визначень.

За винятком тривіальних випадків, коли функції oi і ωj, визначені ясно, канал спостереження є фізичним пристроєм і процедурою, що описує його застосування. Цей пристрій звичайно називається вимірювальним приладом або інструментом. Процедура є набором команд, що визначають те, як слід використовувати інструмент в різних умовах.

Будь-який вимірювальний інструмент повинен уміти взаємодіяти з вимірюваною властивістю і перетворювати цю взаємодію у вигляд, що безпосередньо представляє стани відповідної змінної (наприклад, свідчення покажчика на шкалі буквено-цифрового дисплея або просто запис значень).

Не дивлячись на те, що вимірювальні інструменти і процедури, створюючі канали спостереження, повинні відповідати деяким загальним принципам вимірювання, вони істотно залежать від того, що вони вимірюють. Тому їх вивченням, створенням і використанням займаються, головним чином, в рамках традиційних наукових дисциплін.

Канали спостереження враховуються в схемі АСНД тільки як компоненти, необхідні для повного визначення будь-якої реально існуючої системи. У АСНД вони достатньо часто не включаються.

Приклад 1.1. Для ілюстрації введених понять покладемо, що ai - це встановлений щорічний дохід платника податків деякої країни за останній рік, як повідомляється в його податковій декларації за цей рік. Тоді Ai - це всілякі суми грошей від нуля до максимально уявної суми, скажемо до 100000.00 одиниць. Ця множина звичайно, оскільки мінімальна грошова величина, що має ходіння, - 0.1 одиниці. Ми розуміємо також, що ця множина повністю (лінійно) впорядкована. Для обчислення прибуткового податку досить розглядати тільки діапазони оподатковуваного податком доходу, де кожному діапазону відповідає певний відсоток доходу, який слід виплатити як прибутковий податок. Для спрощення будемо цими діапазонами рахувати діапазони 0-4999.99, 5000.00 - 9999.99, .... 90000.00 -94999.99, 95000.00-100000.00 і хай безліччю станів 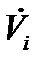, конкретної змінної, що представляє властивість ai, буде безліч мінімальних значень цих діапазонів. Змістовне представлення ai з допомогою можна ввести за допомогою функції ai, яка для кожного діапазону будь-якому значенню з діапазону привласнює мінімальне значення в цьому діапазоні, наприклад оi (52357) =50 000 або оi (796) =0. Очевидно, що функція оi гомоморфна щодо повного впорядкування Ai, оскільки для будь-якої пари

би, в Ai, якщо б в, оi(би) оi (в) . З методичних міркувань узагальнена змінна vi може бути для конкретної змінної визначена за допомогою абстрагуючої функції e-1i : m Vi . Ця функція повинна бути ізоморфною щодо впорядкування на . Припустимо, що потрібне, щоб безліч Vi була набором значень цілих чисел. Тоді e-1i можна, ймовірно, найбільш природним чином, задати наступним рівнянням:

e-1i (5000k)=k (k=0,1,., 19)

Базою в даному прикладі є безліч платників податків певної категорії, скажемо безліч жителів міста Х. Данноє множина не володіє ніякими математичними властивостями. Таким чином, ωj : Bj → 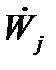 може бути будь-який взаємно однозначною функцією, яка кожному платнику податків ставить у відповідність унікальний ідентифікатор. Методологічно зручно абстрагування ε-1j: 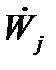→Wj представити у вигляді взаємно однозначної функції, що ставить у відповідність цілим числам

з безлічі Nn, де n - число платників податків в цій групі.