Виходячи зі всього вищесказаного, система може бути визначена як безліч властивостей, з кожним з яких пов'язано безліч його проявів, і безліч баз, з кожною з яких пов'язано безліч її проявів.

Формально система

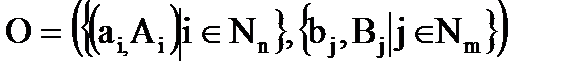,(1.1)

де Nn={1, 2 ., n}, а Nm={1, 2 ., m} (буквою N з позитивним цілим індексом тут завжди позначається безліч значень цілих позитивних чисел від 1 до значення цього індексу); через ai і Ai позначені відповідно властивість і безліч його проявів; bj і Bj- база і безліч її проявів, а O - система об'єкту.

 Для деяких ознак і баз безлічі Ai і Bj з рівняння (1.1) визначаються досить добре. У науці, проте, у багатьох випадках ці множини невідомі і можуть бути визначені тільки за допомогою філософських побудов. Проте, незалежно від обставин їх можна пов'язати з добре певними множинами за допомогою конкретних процедур спостереження або вимірювання. ▲

К.Р. № 2

Охарактеризуйте поняття базової властивості, приведіть докладний приклад.

Виберіть деяку систему, і формалізуйте її.

Лекція 3

Змінні і параметри

Змінною називається представлення властивості, тобто образ властивості, визначуваний конкретною процедурою спостереження або вимірювання. Кожна змінна має певне ім'я, що відрізняє її від інших даних змінних, і зв'язується з певною безліччю величин, через які вона себе проявляє. Ці величини звичайно називають станами, (або значеннями) змінною, а вся множина - безліччю станів.

Аналогічно параметром називається операційне представлення бази. Кожен параметр має унікальне ім'я, і з ним зв'язується якась множина; називатимемо його параметричною множиною, а його елементи - значеннями параметра.

По аналогії з властивостями і базами передбачається, що різні спостереження однієї і тієї ж змінної розрізняються по значеннях параметрів. Якщо використовуються два і більш параметра, то їх загальною параметричною множиною є декартовий твір окремих параметричних множин. Необхідно, щоб кожне конкретне значення параметра (із загальної параметричної множини) ідентифікувало одне і лише одне спостереження відповідних змінних.

На окремій безлічі станів або параметричних множинах можуть бути визначені деякі математичні відносини, скажімо, відношення порядку або відстань. Простим прикладом відношення порядку, є відношення між числами розташованими на звичайній числовій осі. Подібні відносини відображають фундаментальні характеристики властивостей і баз в тому ступені, в якій вони властиві відповідним вимірювальним процедурам.

Відмінності в подібних властивостях серед змінних або параметрів, які мають істотне методологічне значення, тобто впливають на методи досліджень, називатимемо методологічними відмінностями. Вони розглядаються пізніше.

На додаток до конкретних, змінним і параметрам, що представляють відповідно певну ознаку або базу, також розглядатимемо узагальнені змінні і параметри. Останні є абстрактними величинами, тобто величини, не визначені через які-небудь властивості або бази. Їх безліч станів і параметричні множини, а також різні відносини, визначені на цих множинах, представляються якимсь відповідним стандартним чином.