Рассмотрим общий случай нагружения упругого тела. Пусть оно закреплено так, что при нагружении невозможно его смещение как жесткого целого. Тело испытывает деформацию под действием обобщенных сил 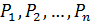 . Энергию упругой деформации выразим функцией этой группы сил:
. Энергию упругой деформации выразим функцией этой группы сил:
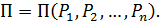
Если одной из внешних сил, например 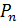 , придать небольшое приращение
, придать небольшое приращение 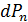 , то энергия упругой деформации возрастает:
, то энергия упругой деформации возрастает:
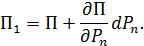
Возьмем другой случай. Допустим, что сначала была приложена бесконечно малая сила 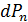 , вызывающая бесконечно малое перемещение. Работой силы
, вызывающая бесконечно малое перемещение. Работой силы 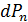 можно пренебречь, как бесконечно малой величиной второго порядка по сравнению с работой приложенных затем сил
можно пренебречь, как бесконечно малой величиной второго порядка по сравнению с работой приложенных затем сил 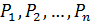 .
.
Потенциальная энергия упругой деформации, вызванной этими силами, по-прежнему равна 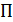 . Кроме того, в точке приложения силы
. Кроме того, в точке приложения силы 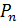 произойдет конечное перемещение
произойдет конечное перемещение 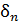 , при котором малая сила
, при котором малая сила 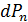 , приложенная вначале, совершит работу
, приложенная вначале, совершит работу 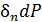 . В итоге накопленная потенциальная энергия деформации будет равна
. В итоге накопленная потенциальная энергия деформации будет равна 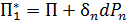 .
.
Потенциальная энергия деформации не зависит от порядка, в котором прикладываются силы, поэтому 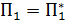 и, следовательно,
и, следовательно,
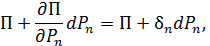
откуда
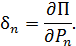
Частная производная от потенциальной энергии упругой деформации по обобщенной силе равна обобщенному перемещению точки приложения силы по направлению силы (теорема Кастильяно). Перемещение точки приложения силы по направлению силы – это проекция на направление силы полного перемещения этой точки.
Выделим из стержня элементарный участок длиной 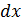 . В общем случае нагружения в поперечных сечениях стержня возникают шесть составляющих внутренних сил:
. В общем случае нагружения в поперечных сечениях стержня возникают шесть составляющих внутренних сил: 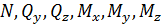 . По отношению к элементарному участку рассмотрим эти внутренние силы как внешние. Определим работу, совершаемую ими при деформировании элемента. Она равна потенциальной энергии, накопленной в элементарном участке стержня. Допустим, что левое сечение элемента неподвижно. Точка приведения сил в правом сечении перемещается. При этом совершается работа. Полная потенциальная энергия элемента стержня может рассматриваться как сумма независимых работ каждого из шести силовых факторов:
. По отношению к элементарному участку рассмотрим эти внутренние силы как внешние. Определим работу, совершаемую ими при деформировании элемента. Она равна потенциальной энергии, накопленной в элементарном участке стержня. Допустим, что левое сечение элемента неподвижно. Точка приведения сил в правом сечении перемещается. При этом совершается работа. Полная потенциальная энергия элемента стержня может рассматриваться как сумма независимых работ каждого из шести силовых факторов:
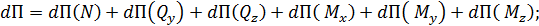
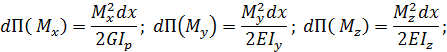
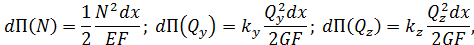
где 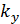 и
и 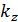 – безразмерные величины, зависящие от геометрической формы сечения.
– безразмерные величины, зависящие от геометрической формы сечения.
Потенциальную энергию всего стержня найдем, проинтегрировав выражение:
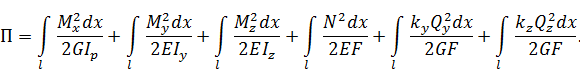
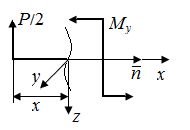
Пример П6.1. Определить перемещение в точке С (рис. П6.2).
Перемещение 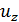 в точке С равно
в точке С равно
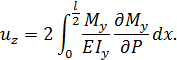
| а | б |
| 
|
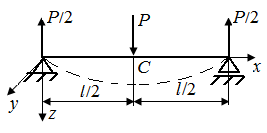
| Рис. П6.2. Схема стержня, нагруженного сосредоточенной силой P (а), и грузового участка с изгибающим моментом My (б) | |
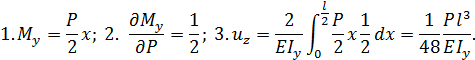
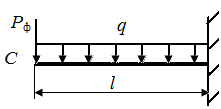
Пример П6.2. Определить перемещение в точке С (рис. П6.3).
| а б | |
| 
|
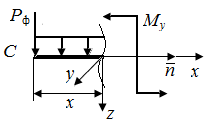
| Рис. П6.3. Схемы стержней с распределенной нагрузкой q и фиктивной силой Pф (а) и грузового участка с изгибающим моментом My (б) | |
При расчете приложим в месте определения перемещения 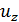 фиктивную силу
фиктивную силу 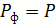 .
.
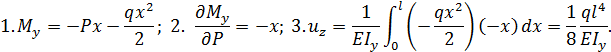
Дата: 2019-02-25, просмотров: 342.