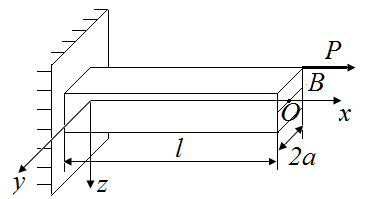
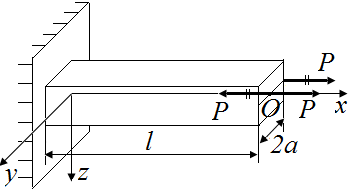
Для определения опорных реакций в стержне (рис. 37, а), сначала определим внешние нагрузки на стержень от силы P, приложенной в точке B . Воспользуемся принципом Сен-Венана:

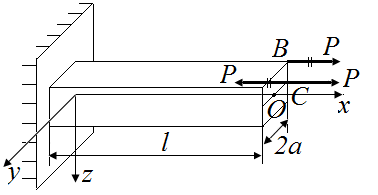
1. К точке С прикладываем две силы, коллинеарные P. Направление одной совпадает с исходной силой P, а другой - противоположное ей             (рис. 37, б). Характер нагрузки на систему не изменился. Получаем пару сил с моментом 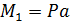, изгибающим стержень относительно оси y и силу P (рис. 37, в).

а	б
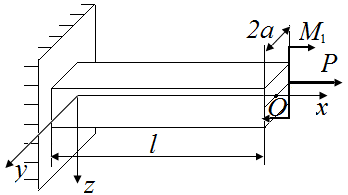
в	г
д	е
Рис. 37. Схемы приведения силы Р к оси стержня

2. Силу, приложенную в точке С, приводим к оси стержня. Прикладываем в точке O две силы, коллинеарные силе P и взаимно противоположно направленные (рис. 37, г). Получаем пару сил с моментом 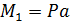, изгибающим стержень относительно оси z и силу P (рис. 37, д). Из условия равновесия определяем два опорных момента  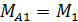и  и 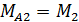опорную реакцию  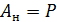(рис. 37, е). Моменты можно переносить в парал­лельную плоскость, от этого характер нагрузки на твердое тело не меняется.

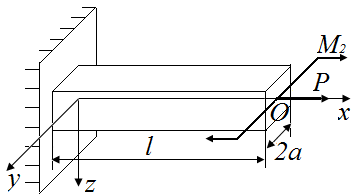
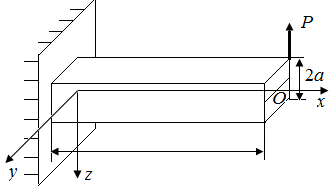
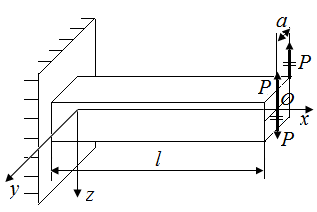
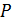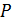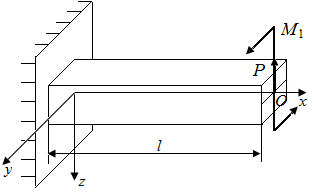
Для определения опорных реакций в стержне (рис. 38, а) определим сна­чала внешние силы, действующие на стержень при приложении нагрузки  в точке В. Воспользовавшись принципом Сен-Венана, приведем силу  в точку O (рис. 38, б). Получаем пару сил с моментом 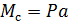, скручивающим стержень относительно оси x, и силу 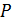, изгибающие стержень в плоскости xOz (рис. 38, в).

а	б
в	г
Рис. 38. Схемы приведения силы Р к оси стержня

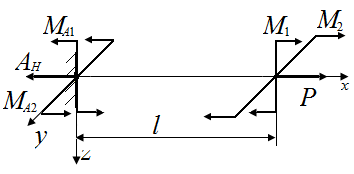
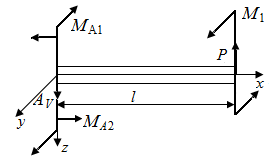
Из условий статического равновесия 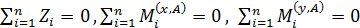 определяем опорные реакции  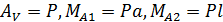(рис. 38, г).

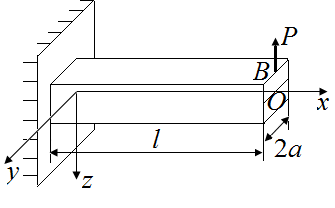
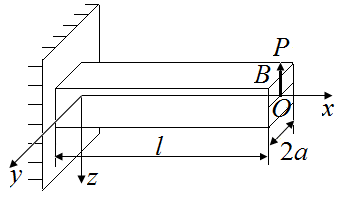
Силу 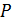, приложенную в точке В (рис. 39, а), можно перемещать по линии действия. От этого характер нагрузки на систему не изменится. Переместим эту силу  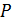в точку О (рис. 39, б). Опорные реакции в стержне определим, используя условия статического равновесия : .

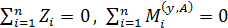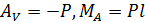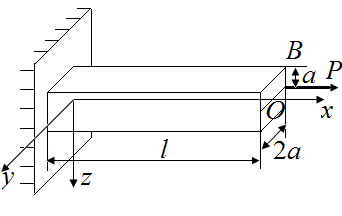
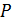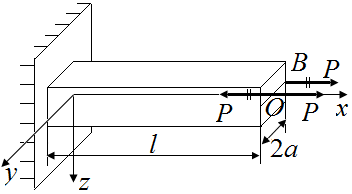
Определим внешние силы, действующие на стержень при приложении силы  в точке В (рис. 40, а). Воспользовавшись принципом Сен-Венана, при­ведем силу 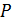 в точку O (рис. 40, б).

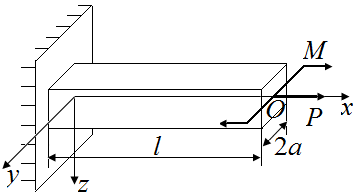
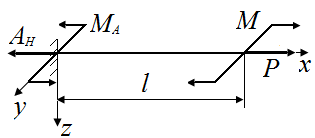
Получим пару сил с моментом 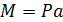, изгибающим стержень в плоскости xOy относительно оси z, и силу 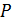, растягивающую стержень   (рис. 40, в).

а	б
Рис. 39. Схемы приведения силы Р к оси стержня

Из условий статического равновесия 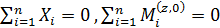 получим .

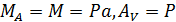а	б
в	г
Рис. 40. Схемы приведения силы Р к оси стержня (принцип Сен-Венана)

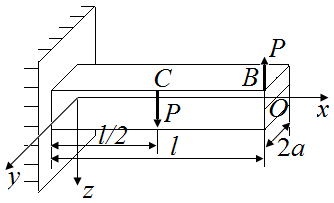
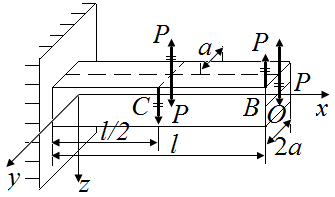
Используя принцип Сен-Венана, приведем силы 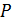, приложенные в точках В, С к оси стержня. Приведение сил определяет нагружение стержня, приведенное на рис. 41.

Моменты 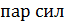 равны по величине 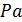, но скручивают стержень в разных направлениях. Из условия статического равновесия  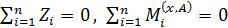опорные реакции .

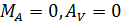а	б
Рис. 41. Схемы приведения силы Р к оси стержня