Р.7.1. Динамические напряжения 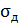 в элементе конструкции (рис. 32, а) определяются по формуле
в элементе конструкции (рис. 32, а) определяются по формуле 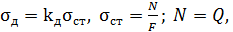 (где
(где 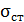 – статическое напряжение,
– статическое напряжение, 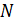 – нормальная сила,
– нормальная сила, 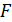 – площадь поперечного сечения,
– площадь поперечного сечения, 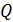 – сила тяжести груза,
– сила тяжести груза, 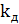 – коэффициент динамичности. Для анализа используем приближенную формулу коэффициента динамичности
– коэффициент динамичности. Для анализа используем приближенную формулу коэффициента динамичности 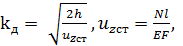 (где – статическое перемещение в месте приложения нагрузки,
(где – статическое перемещение в месте приложения нагрузки, 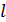 – длина элемента конструкции,
– длина элемента конструкции, 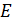 – модуль нормальной упругости материала элемента. Динамические напряжения при растяжении стержня равны
– модуль нормальной упругости материала элемента. Динамические напряжения при растяжении стержня равны 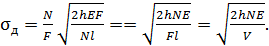 Уменьшение в 4 раза объема стержня или площади его поперечного сечения или длины приводит к увеличению динамического напряжения в два раза, а уменьшение радиуса поперечного сечения в четыре раза приводит к увеличению напряжения в 4 раза. Уменьшение в четыре раза высоты падения груза h, или веса падающего груза
Уменьшение в 4 раза объема стержня или площади его поперечного сечения или длины приводит к увеличению динамического напряжения в два раза, а уменьшение радиуса поперечного сечения в четыре раза приводит к увеличению напряжения в 4 раза. Уменьшение в четыре раза высоты падения груза h, или веса падающего груза 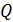 , или модуля нормальной упругости материала стержня приводит к уменьшению динамического напряжения в два раза.
, или модуля нормальной упругости материала стержня приводит к уменьшению динамического напряжения в два раза.
Динамические напряжения 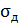 в стержне, представленном на рис. 32, б, определяются по формуле
в стержне, представленном на рис. 32, б, определяются по формуле 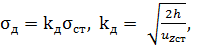 (
( 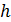 – высота падения груза
– высота падения груза 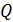 ,
, 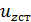 – статическое перемещение в месте падения груза под действием силы
– статическое перемещение в месте падения груза под действием силы 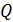 . Статическое перемещение в стержне под действием силы
. Статическое перемещение в стержне под действием силы 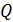 (рис. 32, б)
(рис. 32, б) 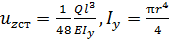 (
( 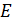 – модуль нормальной упругости материала элемента,
– модуль нормальной упругости материала элемента, 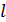 – длина стержня,
– длина стержня, 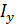 – осевой момент инерции,
– осевой момент инерции, 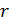 – радиус круглого поперечного сечения). Коэффициент динамичности равен
– радиус круглого поперечного сечения). Коэффициент динамичности равен 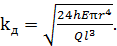 При увеличении параметров
При увеличении параметров 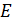 и
и 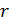 в четыре раза динамические напряжения возрастают, соответственно, в два раза и в шестнадцать раз.
в четыре раза динамические напряжения возрастают, соответственно, в два раза и в шестнадцать раз.
Максимальные касательные динамические напряжения на боковой поверхности вала (рис. 32, в) при резкой остановке определяются по формуле 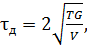 (
( 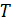 – кинетическая энергия,
– кинетическая энергия,  – модуль упругости при сдвиге,
– модуль упругости при сдвиге, 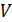 – объем вала). При увеличении в четыре раза длины стержня, или площади поперечного сечения, или объема вала, касательные динамические напряжения
– объем вала). При увеличении в четыре раза длины стержня, или площади поперечного сечения, или объема вала, касательные динамические напряжения 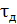 уменьшатся в два раза. При увеличении модуля упругости при сдвиге
уменьшатся в два раза. При увеличении модуля упругости при сдвиге  в четыре раза напряжение
в четыре раза напряжение 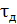 увеличивается в два раза.
увеличивается в два раза.
Р.7.2. Динамические напряжения в стержне определяются формулой 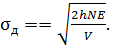 При увеличении высоты падения груза в девять раз динамические напряжения вырастают в три раза.
При увеличении высоты падения груза в девять раз динамические напряжения вырастают в три раза.
ПРИЛОЖЕНИЕ
П1. Основные понятия прикладной механики
Внешняя сила – мера взаимодействия физических объектов. Если какое-либо тело рассматривают изолированно от окружающих его тел, то действие последних заменяют внешними силами.
Деформация – изменение формы и размеров тела в результате внешнего воздействия. Деформацию считают упругой, если она исчезает после устранения вызвавшей ее силы. В противном случае, деформацию называют остаточной.
Упругость – свойство тела проявлять упругую деформацию.
Пластичность – свойство тела проявлять остаточную деформацию.
Прочность – способность конструкции или отдельных ее элементов выдерживать заданную нагрузку, не разрушаясь.
Жесткость – способность конструкции сопротивляться образованию деформаций.
Устойчивость – способность конструкции противостоять воздействиям, стремящимся вывести ее из исходного состояния равновесия.
По времени действия внешние силы разделяют на постоянные, действующие все время существования изделия, и временные, действующие лишь в течение некоторого промежутка времени.
По характеру действия внешние силы разделяют на статические и динамические. Статические силы сообщают телу малые ускорения, которыми можно пренебречь при исследовании. Динамические силы связаны с возникновением значительных ускорений, которыми пренебрегать нельзя.
Объемные силы распределены по всему объему, занятому телом. Единица объемной силы – ньютон на кубический метр (Н/м3). Рассмотрим некоторое тело (рис. П1.1). Выделим в нем элементарный объем 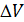 , на который действует объемная сила
, на который действует объемная сила 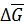 . Среднее значение этой силы находим по формуле
. Среднее значение этой силы находим по формуле
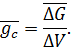
Значение объемной силы в окрестности точки тела равно
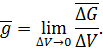
Объемную силу можно разложить по координатным осям х, у, z на составляющие 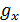 ,
,  ,
, 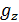 .
.
|
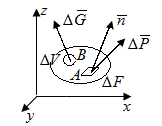
Рис. П1.1. Поверхностная 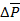 и объемная и объемная 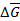 силы, действующие на элементарных участках твердого тела силы, действующие на элементарных участках твердого тела
|
Поверхностные силы распределены по поверхности. Единица поверхностной силы – ньютон на квадратный метр (Н/м2). Выделим в некотором теле на его поверхности элементарную площадку 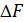 (рис. П1.1). Обозначим через
(рис. П1.1). Обозначим через 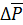 поверхностную силу, действующую на данной элементарной площадке. Среднее значение поверхностной силы определяется по формуле
поверхностную силу, действующую на данной элементарной площадке. Среднее значение поверхностной силы определяется по формуле

Значение поверхностной силы в окрестности точки тела определяет выражение
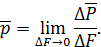
Поверхностную силу можно разложить по координатным осям х, у, z на составляющие 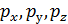 .
.
Если поверхность соприкосновения очень узкая, то можно считать, что сила распределена по линии – распределенная сила. Единица измерения распределенной силы – ньютон на метр (Н/м).
Если площадка, на которой действует поверхностная сила, мала по сравнению с поверхностью всего тела, то поверхностную силу можно считать сосредоточенной в точке тела. Единица сосредоточенной силы - ньютон (Н).
| 
| 
|
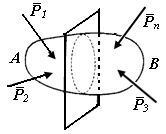
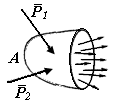
| Рис. П1.2. Внутренние силы в сечении твердого тела | ||
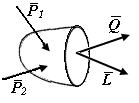
Изменение сил взаимодействия между частицами тела вследствие деформации называют внутренними силами, сопровождающими деформацию. В прикладной механике введено допущение, что тело обладает сплошностью. Для выявления и вычисления внутренних сил применяют метод сечений.
Рассмотрим произвольное тело (рис. П1.2), нагруженное системой сил. Мысленно рассечем его некоторой плоскостью на две части А и В. В точке с обеих сторон сечения будут действовать силы взаимодействия. В зависимости от формы тела и характера приложенных внешних сил интенсивность внутренних сил в различных точках сечения может быть различна. В соответствии с третьим законом Ньютона силы, которые действуют по сечению, принадлежащему части тела А, равны по величине и противоположны по направлению внутренним силам, которые действуют по сечению, принадлежащему части тела В.
Внутренние силы, действующие в сечении, можно привести к одной точке (обычно к центру тяжести сечения), в результате чего на каждой стороне сечения получим главный вектор внутренних сил 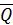 и вектор главного момента внутренних сил
и вектор главного момента внутренних сил 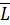 . Для того чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
. Для того чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
|
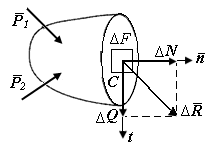
| Рис. П1.3. Элементарная площадка в окрестности точки С |
Рассмотрим сечение А некоторого тела (рис. П1.3). В окрестности точки С выделим элементарную площадку 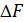 (
( 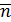 – нормаль к площади сечения). Пусть
– нормаль к площади сечения). Пусть 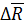 – равнодействующая внутренних сил на площадке,
– равнодействующая внутренних сил на площадке,
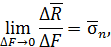
где 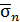 – полное напряжение в окрестности точки С на площадке с нормалью
– полное напряжение в окрестности точки С на площадке с нормалью 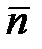 , единица напряжения - Паскаль (Па).
, единица напряжения - Паскаль (Па).
Как равнодействующую внутренних сил 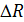 , так и полное напряжение
, так и полное напряжение 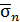 можно разложить на составляющие. Равнодействующую внутренних сил разложим на составляющие
можно разложить на составляющие. Равнодействующую внутренних сил разложим на составляющие 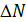 , направленную по нормали к площадке, и
, направленную по нормали к площадке, и 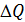 , касательную к площадке. Полное напряжение разложим на нормальное напряжение, действующее в окрестности точки С на площадке с нормалью
, касательную к площадке. Полное напряжение разложим на нормальное напряжение, действующее в окрестности точки С на площадке с нормалью 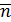 ,
,
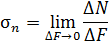
и касательное напряжение, действующее в окрестности точки С на площадке с нормалью 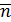 по направлению
по направлению 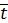 ,
,

Касательное напряжение имеет два индекса – нормали и касательной к площадке.
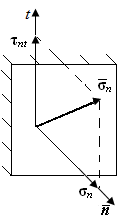
Рассмотрим площадку с нормалью 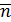 , взятую в окрестности некоторой точки деформируемого тела (рис. П1.4). Полное напряжение в общем случае не совпадает с направлением нормали. Его проекции на направление нормали
, взятую в окрестности некоторой точки деформируемого тела (рис. П1.4). Полное напряжение в общем случае не совпадает с направлением нормали. Его проекции на направление нормали 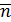 и касательной обозначим соответственно
и касательной обозначим соответственно 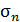 и
и 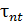 , тогда
, тогда
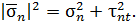
| 
|
Рис. П1.4. Составляющие 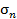 , , 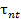 полного напряжения на элементарной площадке полного напряжения на элементарной площадке
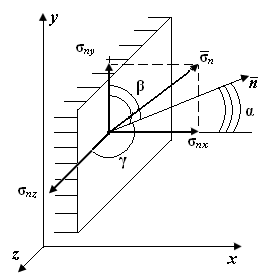
| Рис. П1.5. Проекции полного напряжения 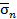 на координатные оси на координатные оси 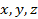
|
Если нормаль к площадке составляет с координатными осями 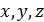 углы
углы 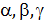 , то нормальную составляющую напряжений
, то нормальную составляющую напряжений 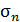 можно найти через проекции полного напряжения на координатные оси
можно найти через проекции полного напряжения на координатные оси 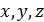 (рис. П1.5)
(рис. П1.5)
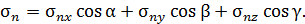
При повороте площадки напряжение в окрестности точки деформированного тела изменяется.
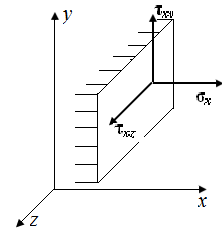
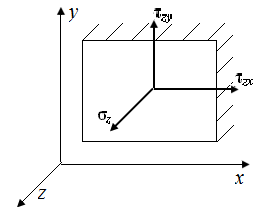
Для полной характеристики напряженного состояния в окрестности точки тела необходимо знать напряжения на трех взаимно перпендикулярных площадках, проведенных через эту точку (рис. П1.6). Девять напряжений 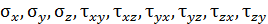 – составляющие полных напряжений, действующих на трех ортогональных площадках в окрестности точки твердого деформированного тела.
– составляющие полных напряжений, действующих на трех ортогональных площадках в окрестности точки твердого деформированного тела.
Если внешняя нормаль к площадке совпадает с положительным направлением оси координат, то положительные составляющие напряжений направлены в положительную сторону осей координат. Если внешняя нормаль к сечению направлена в сторону, противоположную положительному направлению оси координат, то положительные составляющие напряжений направлены в стороны, противоположные соответствующим направлениям осей координат.
| 
| 
|
| Рис. П1.6. Составляющие напряжений | ||
Напряженное состояние в окрестности тела характеризуется девятью составляющими напряжений, которые обычно записывают в виде тензора напряжений
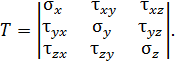
Выделим в твердом теле точку А (рис. П1.7). Пусть под действием внешних сил эта точка займет положение 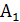 . Отрезок AB называют вектором полного упругого перемещения
. Отрезок AB называют вектором полного упругого перемещения 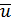 . Проекции вектора полного упругого перемещения на оси декартовой системы координат х, у, z обозначают
. Проекции вектора полного упругого перемещения на оси декартовой системы координат х, у, z обозначают 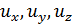 и называют составляющими перемещений точки.
и называют составляющими перемещений точки.
Различают два вида деформации тела: относительное удлинение в окрестности точки и относительный сдвиг.
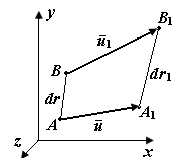
Величина 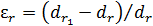 (рис. П1.7) - относительное удлинение в окрестности точки
(рис. П1.7) - относительное удлинение в окрестности точки 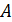 по направлению
по направлению 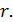 Относительное удлинение будем считать положительным, если бесконечно малые отрезки увеличиваются по длине.
Относительное удлинение будем считать положительным, если бесконечно малые отрезки увеличиваются по длине.
| 
|
| Рис. П1.7. Удлинения в окрестности точки А твердого тела в направлении r | Рис. П1.8. Изменение прямого угла в окрестности точки А при деформации твердого тела |
Рассмотрим прямой угол, образованный в недеформированном теле двумя отрезками AB и АС (рис. П1.8). После нагружения тела внешними силами этот угол изменяется, принимая значение  . Величину, равную изменению прямого угла после нагружения между двумя взаимно перпендикулярными направлениями называют относительным сдвигом, углом сдвига или просто сдвигом. Относительный сдвиг считается положительным, если прямой угол уменьшается.
. Величину, равную изменению прямого угла после нагружения между двумя взаимно перпендикулярными направлениями называют относительным сдвигом, углом сдвига или просто сдвигом. Относительный сдвиг считается положительным, если прямой угол уменьшается.
Относительные линейные и угловые деформации в направлении координатных осей х, у, z обозначают 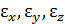 , а изменение углов между этими отрезками –
, а изменение углов между этими отрезками – 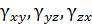 . Величины
. Величины 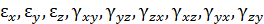 называют составляющими деформации в окрестности точки деформируемого твердого тела. Составляющие деформаций принято записывать в виде тензора, деформации
называют составляющими деформации в окрестности точки деформируемого твердого тела. Составляющие деформаций принято записывать в виде тензора, деформации
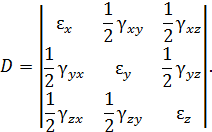
Перемещения и деформации зависят от координат точки тела, а напряжения – от координат точки, через которую проходит площадка (сечение), и от ориентации этой площадки. Составляющие напряжений и деформаций характеризуют напряженно-деформированное состояние точки твердого тела.
Три взаимно перпендикулярных нормальных напряжения, действующие в окрестности точки на площадке, на которых отсутствуют касательные напряжения, называют главными напряжениями:
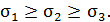
Три взаимно перпендикулярных направления, между которыми отсутствуют углы сдвига, называют главными осями деформации. Относительные удлинения 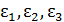 вдоль этих осей называют главными относительными удлинениями.
вдоль этих осей называют главными относительными удлинениями.
В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между нормальным напряжением 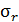 и относительным удлинением
и относительным удлинением 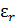
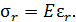
Коэффициент пропорциональности 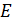 – модуль нормальной упругости – характеризует свойство материала элемента конструкции сопротивляться деформации растяжения.
– модуль нормальной упругости – характеризует свойство материала элемента конструкции сопротивляться деформации растяжения.
Коэффициент пропорциональности между касательным напряжением и относительным сдвигом – модуль упругости при сдвиге G – характеризует свойство материала элемента конструкции сопротивляться сдвигу одного слоя материала конструкции относительно другого.
Взятое по модулю отношение поперечного относительного сжатия тела к относительному удлинению в пределах соблюдения закона Гука называют коэффициентом Пуассона 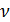 .
.
Величины E и G выражают в Паскалях (Па).
Модуль нормальной упругости E , модуль упругости при сдвиге G и коэффициент Пуассона 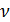 определяют экспериментально.
определяют экспериментально.
Удлинение 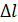 твердого тела длиной l связано с воздействием температуры соотношением
твердого тела длиной l связано с воздействием температуры соотношением
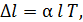
где 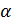 – температурный коэффициент линейного расширения.
– температурный коэффициент линейного расширения.
Если относительное перемещение элементов изделия происходит без деформации, то такую конструкцию называют геометрически изменяемой; если оно происходит только при деформации элементов – геометрически неизменяемой.
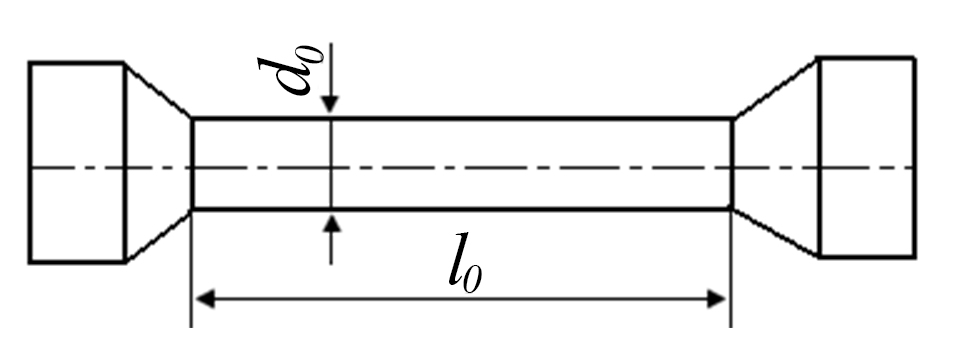
При определении механических свойств конструкционных материалов проводят испытания на растяжение, сжатие, кручение и изгиб образцов, форма и размеры которых стандартизированы (рис. П1.9).
|
| Рис. П1.9. Схема стандартизованного стержня |
Испытания на растяжения выполняют на разрывной машине при нагружении вдоль продольной оси стандартного образца диаметром 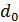 и рабочей частью
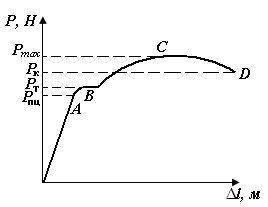
и рабочей частью 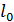 . На рис. П1.10 приведены диаграммы растяжения для пластичного и хрупкого образцов:
. На рис. П1.10 приведены диаграммы растяжения для пластичного и хрупкого образцов:
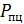 – максимальная нагрузка до которой зависимость между нагрузкой
– максимальная нагрузка до которой зависимость между нагрузкой 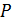 и удлинением образца линейна;
и удлинением образца линейна;
а
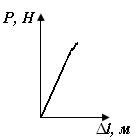
| б
|
| Рис. П1.10. Диаграммы растяжения для пластичного (а) и хрупкого (б) образцов | |
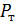 – нагрузка, при которой деформация образца происходит без ее увеличения (стадия текучести материала). После стадии текучести наступает стадия упругости материала. На диаграмме участок до точки С.
– нагрузка, при которой деформация образца происходит без ее увеличения (стадия текучести материала). После стадии текучести наступает стадия упругости материала. На диаграмме участок до точки С.
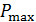 – максимальная нагрузка, которую испытывает образец, по достижении которой, деформация локализуется в ослабленном сечении образца.
– максимальная нагрузка, которую испытывает образец, по достижении которой, деформация локализуется в ослабленном сечении образца.
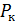 – нагрузка в момент разрушения образца.
– нагрузка в момент разрушения образца.
Для суждения о свойствах материала образца строят диаграмму условных напряжений (рис. П1.11) в системе координат 
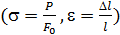 , F0 – первоначальная площадь поперечного сечения образца.
, F0 – первоначальная площадь поперечного сечения образца.
Вычисляют значения механических характеристик материала: характеристик прочности, определяющих способность материала сопротивляться нагрузкам, и характеристик пластичности, определяющих способность материала сопротивляться деформации. Характеристики прочности: предел пропорциональности 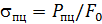 – напряжение, для которого справедлив закон Гука; предел текучести
– напряжение, для которого справедлив закон Гука; предел текучести 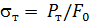 – напряжение,
– напряжение,
при котором деформации растут без заметного увеличения нагрузки (или составляют 0,2% от длины рабочей части образца); временное сопротивление 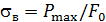 – напряжение, соответствующее максимальной нагрузке, предшествующей разрушению образца; истинное напряжение в момент разрыва
– напряжение, соответствующее максимальной нагрузке, предшествующей разрушению образца; истинное напряжение в момент разрыва 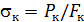 . Характеристики пластичности: относительное удлинение
. Характеристики пластичности: относительное удлинение
после разрыва, %:
|
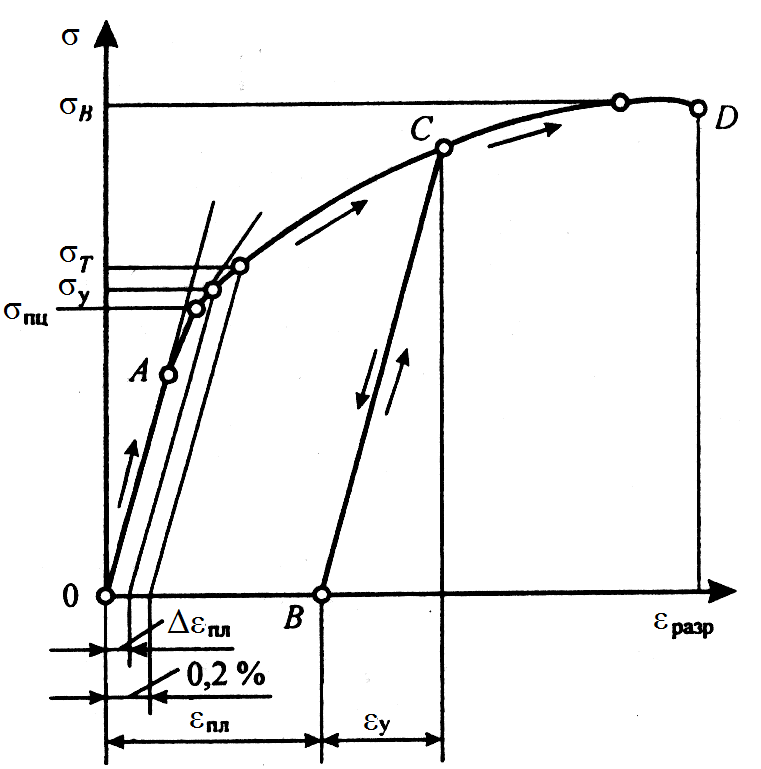
| Рис. П1.11. Диаграмма условных нагружений |
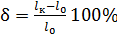 ,
,
относительное сужение поперечного сечения образца после разрыва
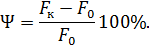
Относительное удлинение e произвольной точки С представляет сумму упругой 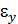 и пластической
и пластической 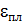 деформации. После разгрузки образца упругая деформация
деформации. После разгрузки образца упругая деформация 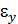 исчезает, а пластическая
исчезает, а пластическая 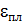 остается.
остается.
Для избежания образования в элементах конструкций заметных остаточных напряжений, за величину опасного напряжения 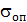 для пластичных материалов принимается обычно предел текучести
для пластичных материалов принимается обычно предел текучести 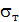 .
.
Для хрупких, а в некоторых случаях и умеренно пластичных материалов за 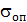 принимают временное сопротивление
принимают временное сопротивление 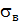 .
.
Расчет напряжений ведется по наибольшему напряжению 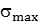 , возникающему в некоторой точке нагруженного тела.
, возникающему в некоторой точке нагруженного тела.
Искомые размеры элемента конструкции получают из условия
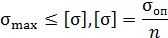
где 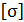 – допускаемое напряжение, n – коэффициент запаса.
– допускаемое напряжение, n – коэффициент запаса.
Пример П1.1. Какие возможности при решении задач дает введение допущений сплошности, однородности и изотропности материала конструкций?
Допущение о сплошности материала элемента конструкции позволяет пользоваться методом анализа бесконечно малых (интегрировать, дифференцировать). Оно приемлемо лишь для тел, размеры которых существенно превышают межатомные расстояния.
Допущение однородности материала допускает, что его свойства (физические и механические) неизменны в пределах рассматриваемой области.
|
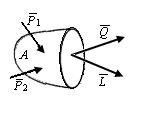
| Рис. П1.12. Главный вектор внутренних сил и вектор главного момента внутренних сил на схеме поперечного сечения стержня |
Допущение анизотропности позволяет считать, что физические и механические свойства не зависят от угловой ориентации элемента конструкции.
Пример П1.2. На какие составляющие раскладываются приведенные к центру тяжести сечения главный вектор внутренних сил и вектор главного момента внутренних сил (рис. П.1.12). Как их называют?
При деформации твердого тела нарушается взаимодействие между его частицами. Это приводит к появлению внутренних сил. Для определения этих сил используют метод сечений. При этом внутренние силы можно представить главным вектором внутренних сил 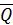 и вектором главного момента
и вектором главного момента 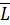 (рис. П1.13, а).
(рис. П1.13, а).
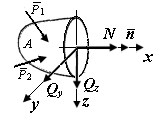
Для удобства вычислений эти векторы раскладывают на составляющие:
а) главный вектор сил на нормальную силу 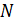 и поперечные силы
и поперечные силы 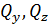 (рис. П1.13, а);
(рис. П1.13, а);
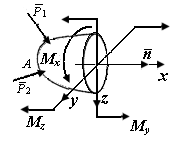
б) вектор главного момента на три пары сил с крутящим моментом  и двумя изгибающими моментами
и двумя изгибающими моментами  и
и 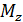 (рис. П1.13, б).
(рис. П1.13, б).
а
| б
|
| Рис. П1.13. Составляющие главного вектора внутренних сил (а) и вектора главного момента внутренних сил (б) | |
Дата: 2019-02-25, просмотров: 410.
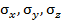 на трех взаимно перпендикулярных площадках
на трех взаимно перпендикулярных площадках