Рассмотрим поперечное сечение стержня, находящегося в состоянии равновесия.
Выделим на нем элементарную площадку и покажем действующие напряжения и внутренние силы (рис. П5.1).
Связь между напряжениями и внутренними силами в сечениях стержней характеризуют следующие интегралы:
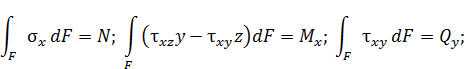
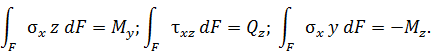
Выражения для напряжений, возникающих в поперечном сечении стержня, нагруженном по торцам, имеют следующий вид:
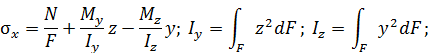
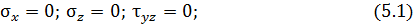
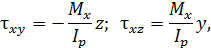
где F – площадь поперечного сечения,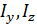 
– осевые моменты инерции сечения относительно осей y и z .
|
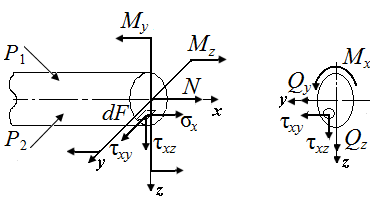
| Рис. П5.1. Внутренние силы в поперечном сечении стержня и напряжения на элементарных площадках |
Полное касательное напряжение в круглом поперечном сечении в окрестности точки на площадке с нормалью х
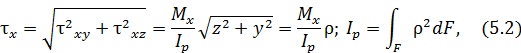
где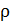 
– текущий радиус, 
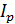– полярный момент инерции.
При осевом растяжении (сжатии) стержня нормальное напряжение
В стержне линейное напряженное состояние. В поперечном сечении напряжения распределены равномерно, если по торцам приложена равномерно распределенная нагрузка и нет резкого изменения сечения тела.
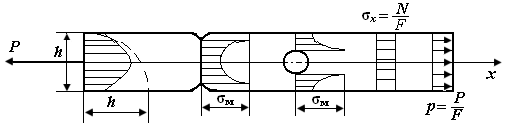
Наличие местных ослаблений (отверстий, выточек) существенно сказывается на напряженно-деформированном состоянии тела. Распределение напряжений в сечениях, близких к месту расположения ослаблений, становится неравномерным (рис. П5.2).
|
| Рис. П5.2. Нормальные напряжения при растяжении стержня с концентрациями напряжений |
По мере удаления от сечений, проходящих через центр отверстия и выточек, эта неравномерность постепенно сглаживается (в пределах расстояния, примерно равного наибольшему поперечному размеру стержня). Около отверстия и выточек имеет место концентрация напряжений. Эти местные напряжения можно вычислить так:
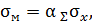
где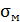 
– местные напряжения; 
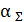– коэффициент концентрации напряжений.
Чтобы стержень под действием нагрузок не разрушается, необходимо соблюдать условие
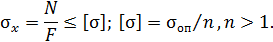
Значение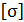 
– допустимого нормального напряжения для данного материала – устанавливают в каждом конкретном случае на основании опытных данных о прочности материала с учетом условий работы объекта. Опасное напряжение 
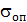зависит от состояния материала: для пластичного состояния за 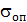принимают 
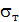, для хрупкого состояния – временное сопротивление 
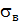. Эти механические характеристики материала определяют по диаграмме условных напряжений материала, полученной в результате испытаний.
Рассмотрим кручение призматического стержня с круглым поперечным сечением. При таком характере деформации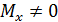 
. В поперечном сечении стержня возникают касательные напряжения
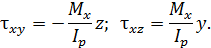
Кубическое уравнение принимает вид
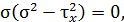
и главные напряжения равны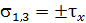 
, 
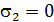. При кручении в окрестности точек поперечного сечения возникает плоское напряженное состояние – чистый сдвиг.
Полное касательное напряжение возникающее в окрестности точки поперечного сечения
Для круглого поперечного сечения выражение для полярного момента инерции принимает вид
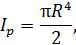
где R – наружный радиус поперечного сечения.
Касательное напряжение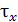 
изменяется по линейному закону и принимает экстремальное значение в точках наружного контура.
При кручении принимают следующее условие прочности:
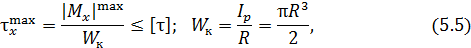
где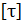 
– допускаемое касательное напряжение.
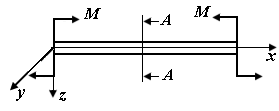
При чистом изгибе (рис. П5.3)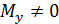 
, и напряжение
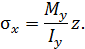
В плоскости хО y напряжение равно 0. Такую плоскость называют нейтральной. След нейтральной плоскости на чертеже – нейтральная линия. В окрестности точек поперечного сечения стержня реализуется линейное напряженное состояние, так как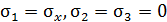 
ниже нейтральной линии и 
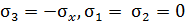выше нейтральной линии. Условие прочности имеет вид
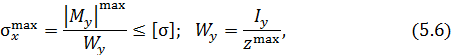
где 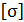– допускаемое нормальное напряжение, 
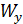– момент сопротивления при изгибе относительно оси y для круглого поперечного сечения
а
| б
|
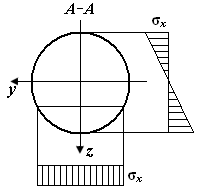
| Рис. П5.3. Чистый изгиб стержня: а – схема стержня, б – распределение нормального напряжения sx в поперечном сечении стержня | |
для прямоугольного
При плоском поперечном изгибе стержня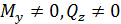 
. В инженерной практике для расчета нормальных напряжений 
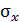используют выражение полученное при чистом изгибе 
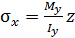и вводят допущения, что касательные напряжения 
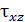вдоль любой прямой, параллельной оси y распределение равномерно.
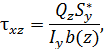
где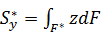 
– статический момент площадки 
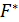относительно оси y; 
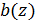– ширина стержня на расстоянии z от его оси.
Для круглого и прямоугольного сечения формула для 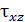принимает вид: для прямоугольного сечения высотой h и шириной b
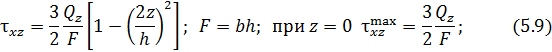
для круглого сечения наружного радиуса R
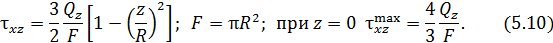
При расчете на прочность при растяжении-сжатии стержней можно связать их разрушение, или возникающие пластические деформации с экстремальными значениями единственного, отличного от нуля главного напряжения (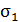 
или 
)
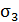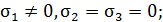
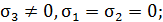
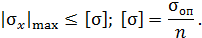
При растяжении, на опасном участке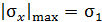 
, а при сжатии 
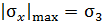. Для хрупкого напряженного состояния 
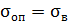, для пластичного напряженного состояния 
.
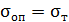В случае плоского и объемного напряженного состояний необходимо учитывать два или три главных напряжений. На возникающие пластические деформации и на разрушение влияют не только эти главные напряжения, но и соотношение между ними.
Высказано несколько предположений о причинах разрушения материала или возникающих пластических деформациях в элементах конструкций:
1. В гипотезе наибольших нормальных напряжений предполагают, что разрушение хрупкого материала происходит в результате того, что самое большое нормальное напряжение в элементе конструкции превышает предельное значение:
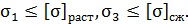
2. В гипотезе наибольших касательных напряжений предполагают, что недопустимые пластические деформации наступают при условии, что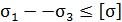 
.
3. В последнее время в инженерной практике для оценки пластического состояния материала наибольшее применение находит теория энергоформообразования:
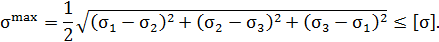
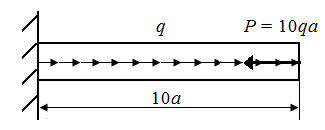
Пример П5.1. Определить опасное сечение и величину экстремального значения напряжения в стержнях круглого поперечного сечения радиуса a, нагруженных в соответствии с рис. П5.4.
|
| Рис. П.5.4. Схема стержня, нагруженного вдоль его оси |
Решение:
1. Определим опорную реакцию в стержне (рис. П5.5, а). Из условия статического равновесия.
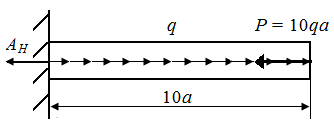
2. Закон изменения нормальной силы определим из условия статического равновесия (рис. П5.5, б)
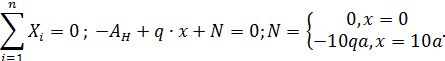
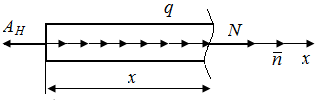
3. Строим эпюр нормальных сил в соответствии с значениями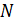 
на границе грузовых участков (рис. П5.5, в).
Экстремальное значение
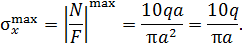
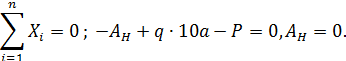
а
|
б
|
в
|
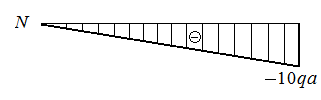
| Рис. П5.5. Опорная реакция A н (а), нормальная сила N (б) и эпюра нормальной силы в стержне (в) (рис. П.5.4.) |
Пример П5.2. Определить величину экстремального значения напряжения в стержне круглого поперечного сечения радиуса r, представленного на рис. П5.6.
Решение:
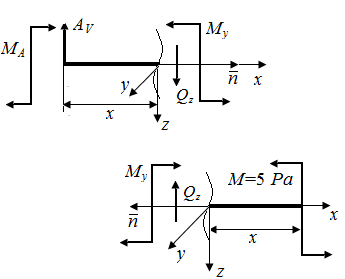
1. Опорные реакции при плоском поперечном изгибе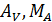 
определим рассматривая два условия статического равновесия (рис. П5.6, а):
2. На каждом из грузовых участков для определения закона изменения поперечной силы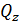 
и изгибающего момента 
также рассматриваем два условия статического равновесия (рис. П5.6, б).
2.1.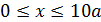 
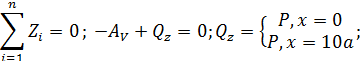
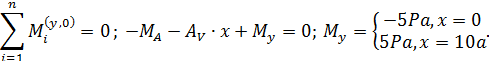
2.2.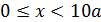 
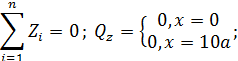
а
|
б
|
в
|
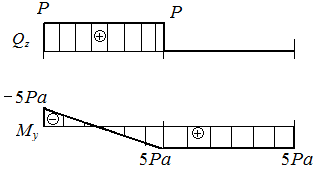
| Рис. П5.6. Опорные реакции AV , MA (а), поперечные силы и изгибающие моменты Qz , My (б) на грузовых участках и эпюры поперечных сил и изгибающих моментов (в) в стержне, испытывающем плоский поперечный изгиб |
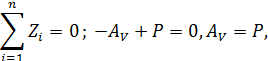
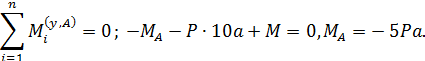
3. По результатам вычислени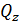й и на границах грузовых участков построены эпюры поперечных сил 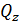и изгибающих моментов (рис. П5.6, в). Экстремальное значение напряжения равно
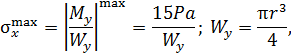
где 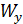– момент сопротивления круглого сечения при изгибе.
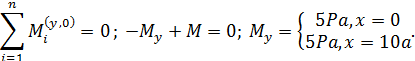
Пример П5.3. Определить опасное сечение и величину экстремального значения напряжения в стержне круглого поперечного сечения радиуса r, нагруженного в соответствии с рис. П5.7
|
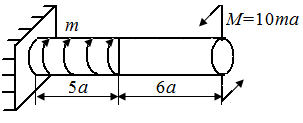
| Рис. П5.7. Схема стержня, испытывающего кручение |
Решение:
1. Из условия статического равновесия стержня определим опорный момент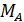 
в стержне, представленном на рис. П5.8, а:
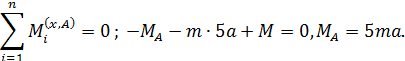
2. Определим значения крутящего момента 
на границах грузовых участков (рис. П5.8, б).
2.1.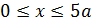 
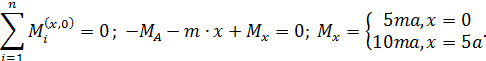
2.2.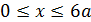 
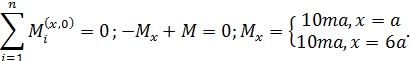
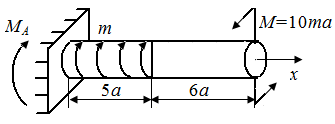
а
|
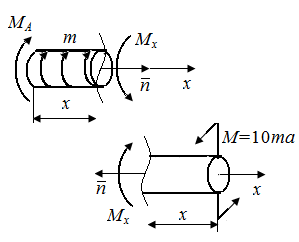
б
|
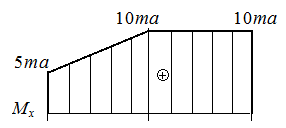
в
|
| Рис. П5.8. Опорный момент MA (а), крутящие моменты Mx (б) на грузовых участках и эпюра крутящих моментов (в) в стержне, испытывающем кручение |
3. На рис. П5.8, в приведена эпюра , построенная по результатам вычислений значений крутящего момента на границах грузовых участков. Экстремальное значение напряжения равно
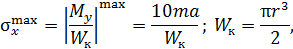
где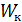 
– момент сопротивления при кручении.
П6. Расчет перемещений
При инженерных расчетах перемещений в стержне с постоянной изгибной жесткостью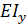 
и одним грузовым участком используют полученное при чистом изгибе ( 
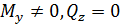) приближенное дифференциальное уравнение изогнутой оси стержня
где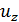 
– перемещение по направлению оси z в окрестности точки, через которую проходит поперечное сечение, нагруженное изгибающим моментом .
При кручении стержня с постоянной жесткостью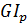 
(G – модуль упругости при сдвиге, 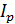– полярный момент инерции), угол поворота определяют используя дифференциальное уравнение угла закручивания поперечного сечения стержня
Формула угла закручивания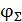 
для стержня, имеющего n участков с различными механическими характеристиками материала на каждом i-м участке, при постоянных, в пределах каждого участка, значениях момента , имеет следующий вид:
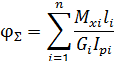
Условие жесткости при кручении стержня характеризуется выражением
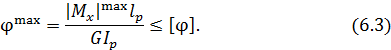
где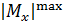 
– наибольший по модулю на эпюре крутящий момент; 
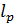– расчетная длина, на которой определяют угол закручивания; 
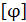– допустимый на данной длине угол закручивания.
Для упрощения вычислений перемещений разработано несколько методов.
Метод начальных параметров.
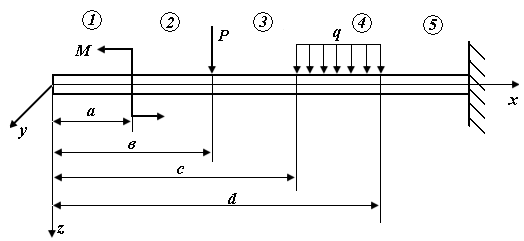
Предположим, стержень (рис. П6.1, а) нагружен сосредоточенным моментом М, приложенным на расстоянии а от левого конца стержня, силой Р на расстоянии b и распределенной нагрузкой q на расстоянии с от начала отсчета. Чтобы обеспечить равенство всех постоянных интегрирования на границах грузовых участков, при составлении дифференциальных уравнений упругой линии и их интегрировании соблюдают следующие правила:
а
|
б
|
в
|
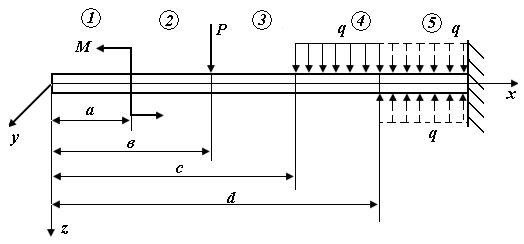
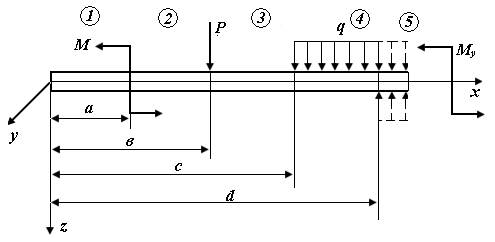
| Рис. П6.1. Схема стержня, нагруженного в плоскости xOz |
1) начало координат выбирают в крайней левой точке стержня;
2) выражение для изгибающего момента составляют применительно к левой отсеченной части стержня;
3) сосредоточенный момент М домножают на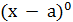 
, что равно единице;
4) распределенную нагрузку продлевают до конца рассматриваемого сечения, а чтобы общий характер внешнего воздействия не изменился, прикладывают «компенсирующую» нагрузку обратного направления (рис. П6.1, б);
5) уравнения для всех участков интегрируют, не раскрывая скобок.
Если на стержень действуют несколько сосредоточенных моментов, сил и распределенных нагрузок, выражения для перемещений и углов поворота в произвольном сечении можно представить в следующем виде:
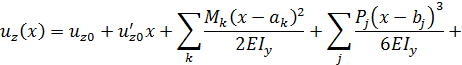
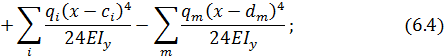
Эти выражения называют универсальными уравнениями упругой линии стержня.
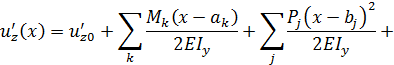
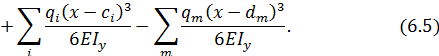
Дата: 2019-02-25, просмотров: 335.
