При деформации твердого тела происходит изменение расстояний между его частицами. Это приводит к нарушению взаимодействия между ними и появлению внутренних сил. Для определения этих сил используют метод сечений.

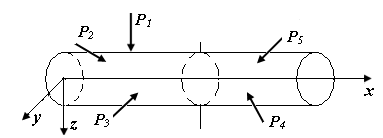
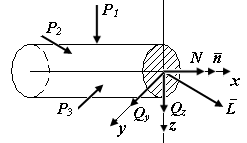
На рис. П3.1, а представлен стержень, находящийся под действием внешних сил в состоянии равновесия. Мысленно рассечем стержень плоскостью, перпендикулярной к оси, на две части и рассмотрим внутренние силы, действующие в плоскости его сечения: главный вектором сил 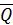 и вектором главного момента  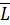(рис. П3.1, б).

а	б
в	г
Рис. П3.1. Внутренние усилия в поперечном сечении стержня

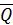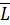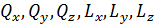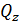Спроецируем силу  и момент  на координатные оси x , y , z -  (рис. П3.1, в, г). Силе  присвоим индекс  (нормальная сила), она вызывает растяжение-сжатие стержня. Силы  и  действуют в плоскости поперечного сечения – поперечные силы.

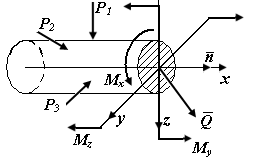
Проекции 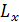 соответствует пара сил с моментом , действующим в плоскости поперечного сечения. Крутящий момент  приводит к деформации кручения.

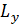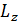Проекциям  и  соответствуют пары сил с моментом  и 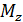, которые лежат в плоскостях, перпендикулярных к этим проекциям. Моменты  и 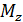 – изгибающие моменты.

Для составляющих внутренних сил вводят следующее правило знаков:

Если внешняя нормаль к сечению 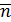 совпадает с направлением оси координат 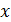, то составляющие внутренних сил 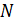,  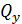и 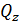 положительны, если они направлены в ту же сторону, что и соответствующие координатные оси. Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х, то составляющие внутренних сил 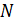,  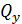и 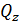 будут положительны, если они направлены в стороны, противоположные направлениям соответствующих координатных осей.

Если внешняя нормаль к сечению совпадает с направлением оси 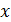, моменты , ,  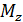считаются положительными, если они действуют против часовой стрелки при рассмотрении с концов соответствующих координатных осей. Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси 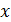, то моменты , ,  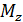будут положительны, если они создают вращение по часовой стрелке при рассмотрении с концов соответствующих координатных осей.

Выделим простейшие виды деформации стержня: осевое растяжение – сжатие ( 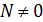); чистый изгиб (в плоскости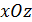 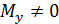, в плоскости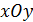 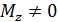); плоский поперечный изгиб (в плоскости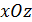 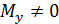, , 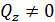в плоскости , ).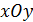

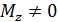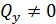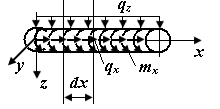
Пусть стержень нагружен в соответствии с рис. П3.2, а.

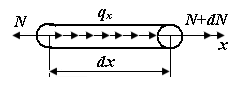
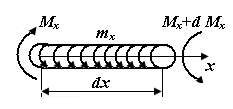
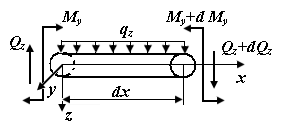
Выделим из стержня элементарный участок длиной 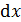 и рассмотрим условия его равновесия (вследствие малости длины элемента силы и моменты можно считать равномерно распределенными).

По рис. П3.2, б

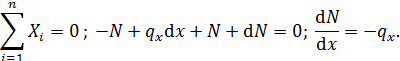
По рис. П3.2, в

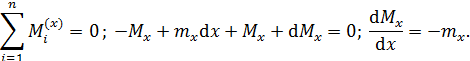
а	б
в	г
Рис. П3.2. Внутренние силы в сечениях элементарного участка стержня

По рис. П3.2, г

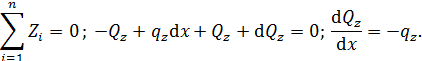
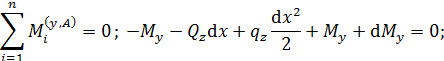
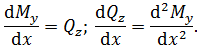
Эпюра внутренних сил отражает распределение их по длине стержня. Участок стержня, на границах которого изменяется характер внешних воздей­ствий, называют грузовым. Определив из условия статического равновесия опорные реакции записывают выражения для внутренних сил на каждом грузовом участке, вычисляют значения внутренних сил на границах участков и строят эпюры внутренних сил.

Пример П3.1. Какое правило знаков вводят для составляющих главного вектора внутренних сил?

Когда направление внешней нормали к сечению 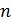 совпадает с направлением оси координат х (левая отсеченная часть стержня), то составляющие внутренних сил  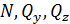положительны, если они направлены в ту же сторону, что и соответствующие координатные оси (рис. П3.3, а).

Когда внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х (правая отсеченная часть стержня), то составляющие внутренних сил 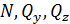 будут положительны, если они направлены в стороны, противоположные направлениям соответствующих координатных осей (рис. П3.3, б).

а                                                      б

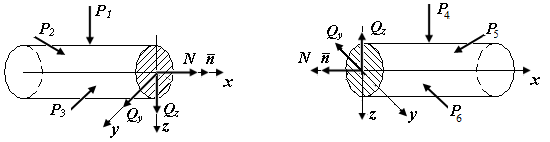
Рис.П3.3. Составляющие главного вектора на схемах левой (а) и правой (б) отсеченных стержней стержня

Пример П3.2. Какое правило знаков вводят для составляющих вектора главного момента внутренних сил.

а                                                            б

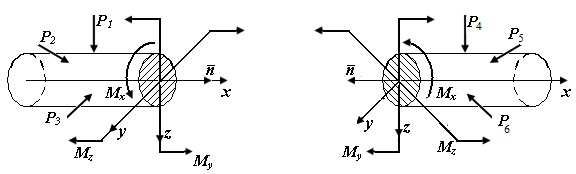
Рис. П3.4. Составляющие вектора главного момента на схемах левой (а) и правой (б) отсеченных частей стержня

Когда направление внешней нормали к сечению 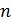 совпадает с направлением оси х, моменты  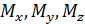считаются положительными, если они действуют против часовой стрелки при рассмотрении с концов соответствующих координатных осей (рис. П3.4, а).

Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х, то моменты 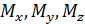 будут положительны, если они создают вращение по часовой стрелке при рассмотрении с концов соответствующих координатных осей (рис. П3.4, б).

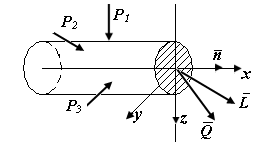
Пример П3.3. Какая разница между силовыми факторами 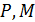          (рис. П3.5) и внутренними силовыми факторам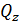и  и ?

Рис. П3.5. Внешние и внутренние силовые факторы на выделенной части стержня, нагруженного в плоскости xOz

Внешние силы выражают меру взаимодействия стержня с другими телами, а внутренние силовые факторы  и  – изменение сил межатомного взаимодействия при деформации стержня.