Напряжения на наклонной площадке (формулы Коши) . Допустим, что известны все составляющие тензора напряжений в точке А деформируемого тела и положение нормали к площадке относительно координатных осей 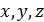задано соответственно углами a, b, g (рис. П4.1).

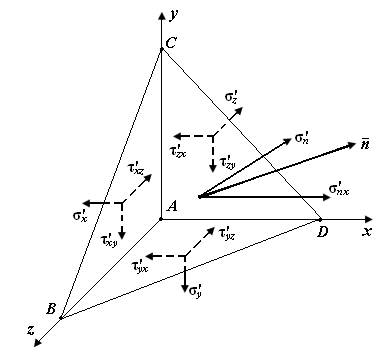
Рис. П4.1. Элементарный тетраэдр в окрестности точки А деформированного тела

Проекции полного напряжения на площадке с нормалью 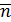 имеют следующий вид (формулы Коши): 

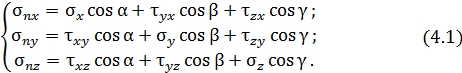
С помощью уравнения Коши можно вычислить напряжения на любой известной площадке, проведенной через точку, если известны компоненты тензора напряжений в этой точке.

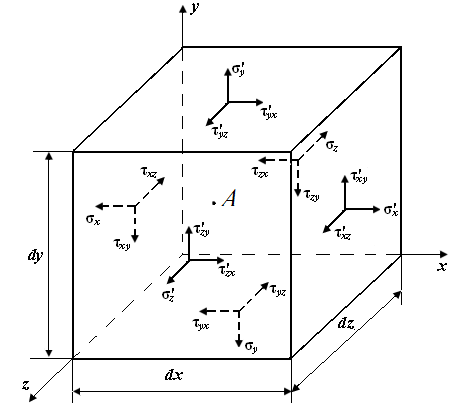
Дифференциальные уравнения равновесия. Свойство парности касательных напряжений. Из условий статического равновесия элементарного объема в форме прямоугольного параллелепипеда (рис. П4.2).

Составив уравнение проекций сил, действующих на гранях элементарного параллелепипеда (рис. П4.2), на оси :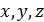

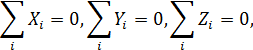
получаем систему дифференциальных уравнений, устанавливающих зависимость между составляющими тензора напряжений и проекциями объемных сил на направления осей .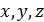

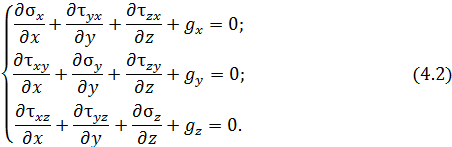
Составив уравнение моментов всех сил, действующих на гранях параллелепипеда, относительно координатных осей:

получим равенства

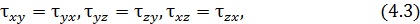
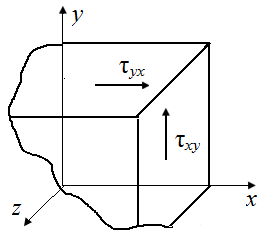
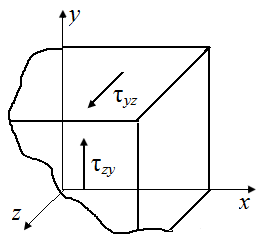
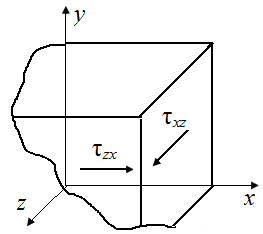
отражающие свойство парности касательных напряжений. На двух взаимно перпендикулярных площадках составляющие касательного напряжения, перпендикулярное к линии пересечения этих площадок, равны между собой по модулю (рис. П4.3)

Рис. П4.2. Элементарный прямоугольный параллелепипед в окрестности точки А деформированного тела

Число компонент тензора напряжений сокращается с девяти до шести и становится симметричным относительно главной диагонали

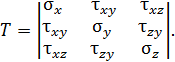
Рис. П4.3. Касательные напряжения на схемах взаимно перпендикулярных площадок прямоугольного параллелепипеда, вырезанного из деформированного тела

Нормальные и касательные напряжения на произвольно ориентированных площадках. Для определения нормальных 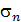 или касательных  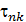напряжений на площадке, нормаль  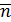к которой составляет углы a, b, g, а касательная k углы a₁ b₁ g₁ с осями координат x , y , z в окрестности точки А достаточно спроецировать полное напряжение, действующее на этой площадке, на направления нормали или касательной. Для этого следует напряжения  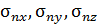определенные по (4.1) умножить соответственно на косинусы углов a₁, b₁, g₁.

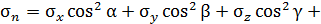
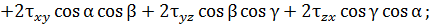
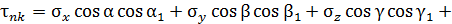
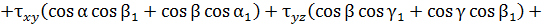
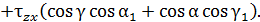
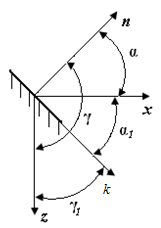
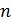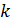Если направления  и  лежат в одной плоскости, например, в плоскости xOz (рис. П4.4): 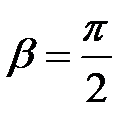; ; 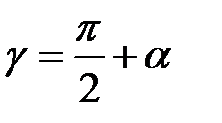 ; 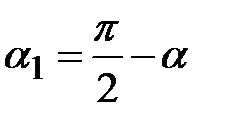g₁=a; cosg=-sina; cosa₁=sina; cosg₁=cosa.

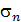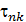Уравнения для  и принимают следующий вид:

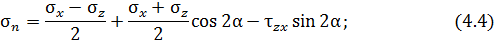
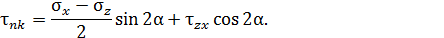
Рис. П4.4. Схема направлений n и k в одной плоскости

Главные площадки и главные напряжения. Экстремальные значения нормальных напряжений. Кубическое уравнение. Площадки, на которых отсутствуют касательные напряжения называются главными, а нормальные напряжения, действующие на них – главными напряжениями.

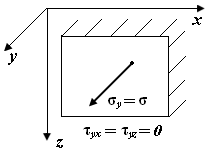
Предположим, что одна из таких площадок известна. Полное напряжение на ней 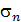 направлено по нормали, которая составляет с координатными осями x , y , z углы a, b, g (рис. П4.5).

Рис. П4.5. Схема положения главной площадки

Система уравнений определяющая положение главных площадок (если известны главные напряжения), или главных напряжений (если известны главные площадки) имеет вид:

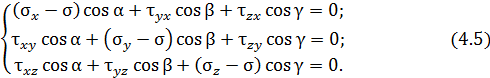
Положение главной площадки определяется углами a, b, g. На главных площадках реализуются экстремальные значения нормальных напряжений.

Система уравнений (4.5) имеет ненулевое решение, если ее определитель, составленный из коэффициентов при неизвестных косинусах, равен нулю:

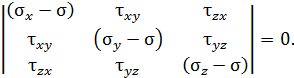
Раскрывая определитель, получаем кубическое уравнение:

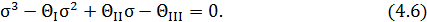
Все корни кубического уравнения являются вещественными и определяют нормальные напряжения, действующие на главных площадках. Их обозначают 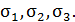 Принято считать, что .

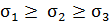Коэффициенты 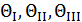 – инварианты тензора напряжений.

В окрестности точки деформированного тела различают напряженное состояние трех видов: линейное ( 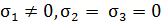), плоское ( 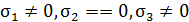), объемное ( ).

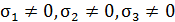Пусть в некоторой точке тела известно положение одной из главных площадок (рис. П4.5, б). Ось x перпендикулярна к этой площадке. Нормальное (главное) напряжение на ней .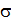

Тензор напряжений принимает следующую форму:

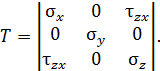
Система уравнений (4.5) имеет вид:

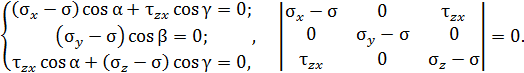
Возможны два решения системы

1) 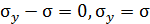 – по условию задачи;

2)

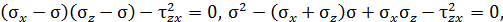
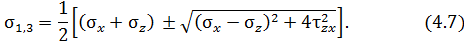
На главных площадках касательные напряжения равны нулю. По (4.5) положение главных площадок определяет выражение:

Касательное напряжение принимает экстремальные значения на площадках, составляющих угол 45⁰ с главными площадками. При этом

 Связь между деформациями и перемещениями в окрестности точки. Шесть дифференциальных зависимостей, связывают составляющие деформаций с составляющими напряжений (впервые получены Коши и носят его имя):

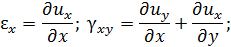
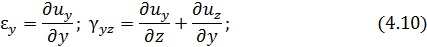
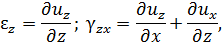
где: 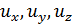 – проекции перемещений в окрестности точки деформированного тела;  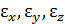– относительные удлинения по направлению осей x , y , z в окрестности точки;  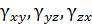– углы сдвига в окрестности этой точки между направлениями xy, yz и zx.

Составляющие деформаций зависят друг от друга, так как они являются производными трех произвольных функций. Функции 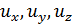 – непрерывные, а значит, и  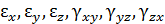должны быть такими, чтобы обеспечить эту непрерывность. Условия сплошности тела в процессе деформации можно рассматривать как условия совместности деформаций.

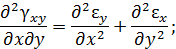
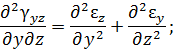
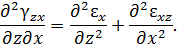
Выражения для определения линейной 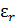 и угловой  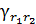деформаций в произвольном направлении  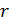и между двумя произвольными взаимно перпендикулярными направлениями  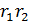по заданным составляющим тензора деформаций имеют следующий вид:

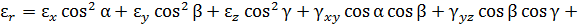
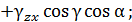
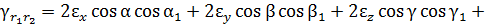
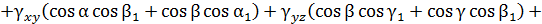
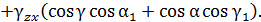
 Закон Гука в обобщенном виде. Допустим, что деформируемое твердое тело однородно и изотропно. Тогда в силу однородности связи между напря­жениями и деформациями во всех точках тела будут одина­ковыми, а в силу изотропности при любом нагружении глав­ные оси деформации совпадут с главными осями напряжений. Отсюда можно считать, что главные деформации являются функциями только главных напряжений, а главные напряже­ния – только главных деформаций:

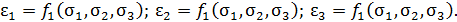
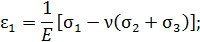
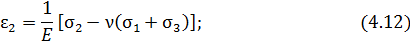
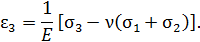
Относительные удлинения по направлению x , y , z и относительные сдвиги между направлениями 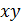, , 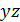 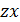определяет следующие соотношения:

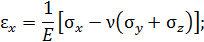
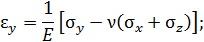
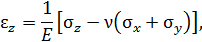
где 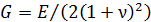 – модуль нормальной упругости при сдвиге.