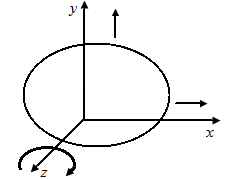
Независимые параметры, однозначно определяющие положение абсолютно твердого тела в плоскости и пространстве называют степенями свободы. В плоскости тело имеет три степени свободы (рис. П2.1, а), в пространстве – шесть (рис. П2.1, б).

а	б
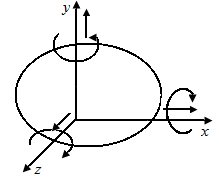
Рис. П2.1. Схема твердого тела с указанием возможных перемещений в плоскости (а) и пространстве (б)

Для превращения тела в элемент конструкции, способный воспринимать нагрузку, у него нужно устранить хотя бы одну степень свободы. Фактор, устраняющий одну степень свободы называют связью.

Для получения геометрически неизменяемого элемента конструкции, на него необходимо накладывать число связей, равное числу степеней свободы (рис. П2.2).

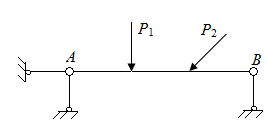
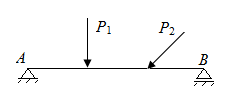
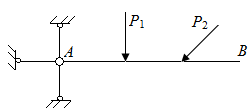
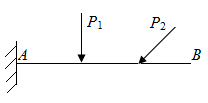
В геометрически неизменяемых конструкциях на стержни, нагруженные в плоскости, накладываются три связи (рис. П2.2, а, б). На расчетных схемах рис. П2.2 приняты условные обозначения для случаев наложения: 1) одной связи в точке B на рис. П2.2, б; 2) двух связей в точке А на рис. П2.2, б; 3) трех связей в точке А на рис. П2.2, г.

Таким образом, все многообразие опорных устройств конструкций сводят к трем основным видам:

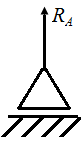
Шарнирно – подвижная опора (рис. П2.3, а) – по линии накладываемой связи может возникнуть одна опорная реакция Ra.

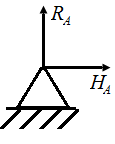
Шарнирно-неподвижная опора (рис. П2.3, б) – по линиям накладываемых связей могут возникнуть две опорные реакции R _А и Н_А.

а	б
в	г
Рис. П2.2. Схемы стержней с различными условиями накладываемых связей

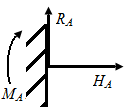
Защемление (жесткое защемление, заделка (рис. П2.3, в) – возникают три составляющие: вертикальная R _А, горизонтальная Н_А и опорный момент М_А.

Все реакции и момент считаются приложенными в точке А – центре тяжести опорного сечения.

Консолью называют стержень, который не имеет других опор, кроме защемленного конца, или часть стержня, выступаю­щую за опоры                    (рис. П2.3, г).

Введем еще ряд понятий.

Жесткий узел – конструктивный узел, в котором концы всех стержней соединены между собой жестко (рис. П2.3, е).

Рама – стержневая система, стержни которой во всех или некоторых узлах жестко соединены между собой (рис. П2.3, ж).

Пространственная система – система, способная воспринимать прило­женную к ней пространственную систему сил.

Плоская система – система, способная воспринимать нагрузки, которые действуют в одной плоскости (рис. П2.3, д).

На схеме стержень принято заменять его осью (рис. П2.3, г, д). При этом все внешние силы должны быть приведены к оси стержня.

При анализе расчетной схемы применяют три основных принципа.

Принцип относительной жесткости основан на том, что в большинстве случаев форма тела под действием внешних сил изменяется несущественно. Это позволяет при составлении уравнений равновесия рассматривать тело как недеформированное, обладающее теми же геометрическими размерами, которое оно имело до нагружения.

а	б	в		г
д			е		ж
Рис. П2.3. Схемы опорных устройств стержней

Применение принципа суперпозиции при большом числе внешних сил позволяет получить решение как результат наложения частных решений.

Применение принципа Сен-Венана позволяет считать, что если в пределах некоторой области упругого тела приложена система сил, то на расстояниях, существенно превышающих характерные размеры взятой области, напряжения и деформации практически одинаковы для всех статически эквивалентных систем сил.

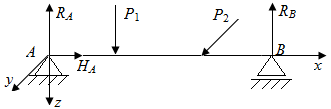
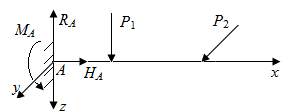
По линии действия связей при нагружении стержня возникают опорные реакции: усилия по линии накладываемых связей в шарнирных подвижной и неподвижной опорах и две опорные реакции и момент в заделке (рис. П2.4) в плоскости, проходящей через точку А (рис. П2.5)

Рис. П2.4. Усилия по линиям накладываемых связей в шарнирных опорах	Рис. П2.5. Усилия по линиям накладываемых связей в заделке

В статически определимых системах опорные реакции определяются при раскрытии условий статического равновесия:

а) для плоской системы

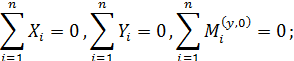
б) для пространственной системы

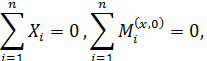
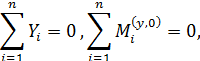
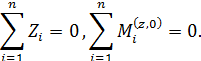
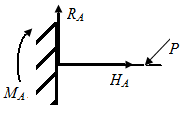
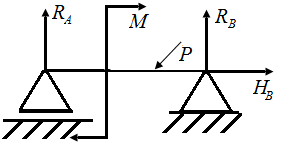
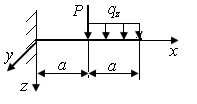
Пример П2.1. Достаточно ли условий статического равновесия для опре­деления опорных реакций в стержне, приведенном на рис. П2.6, а, б?

а	б
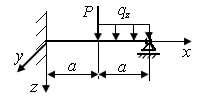
Рис. П2.6. Схемы стержней, нагруженных в плоскости xOz

Стержни, представленные на рис. П2.6, нагружены в плоскости xOz. Условия статического равновесия определяются тремя уравнениями, которые позволяют определить три неизвестных опорных реакции.

На стержень, приведенный на рис. П2.6, а, накладываются четыре связи. Система статически неопределима. На стержень, приведенный на рис. П2.6, б, накладываются три связи – система статически определима.