Р.4.1. Напряженное состояние в окрестности точки, а, следовательно, и главные напряжения 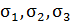 , не могут меняться при изменении системы координат, кубическое уравнение должно быть инвариантно к преобразованию системы координат.
, не могут меняться при изменении системы координат, кубическое уравнение должно быть инвариантно к преобразованию системы координат.
Р.4.2. Коэффициенты кубического уравнения 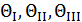 называют инвариантами тензора напряжений, потому что из значения от выбранной системы координат.
называют инвариантами тензора напряжений, потому что из значения от выбранной системы координат.
Р.4.3. При плоском напряженном состоянии, нормальное 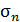 и касательное
и касательное 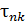 напряжения на площадке (рис. 45), нормаль к которой повернута на угол
напряжения на площадке (рис. 45), нормаль к которой повернута на угол 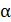 по отношению к площадке, нормальной к оси x определяют выражения:
по отношению к площадке, нормальной к оси x определяют выражения:
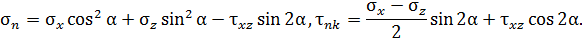
Значения главных напряжений и положения главных площадок определяют выражения:
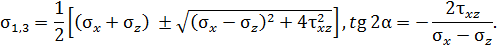
а
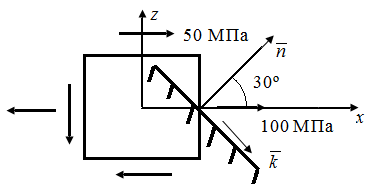
| б
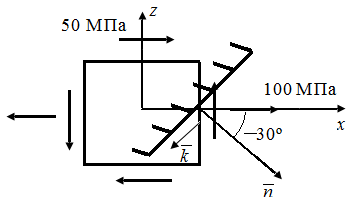
|
| Рис. 45. Схема плоского элемента, выделенного в твердом деформированном теле | |
По условию, заданному на рис. 45 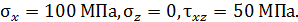 Напряжения на наклонной площадке, повернутой на угол
Напряжения на наклонной площадке, повернутой на угол 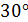 и
и 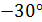 определяют выражения:
определяют выражения:
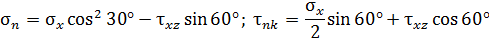
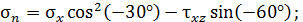
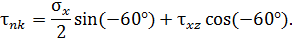
В первом случае 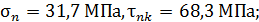 а во втором случае
а во втором случае 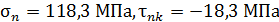 .
.
Значения главных напряжений и положения главных площадок определяют выражения 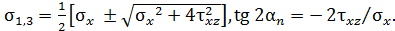
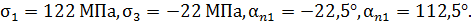
Р.4.4. В примере, представленном на рис. 43 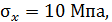
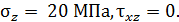 Напряжения на площадках, нормаль к которым повернута относительно оси x на углы
Напряжения на площадках, нормаль к которым повернута относительно оси x на углы 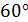 и
и 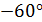 , определим по формулам из Р.4.3:
, определим по формулам из Р.4.3: 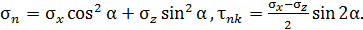
При повороте на угол 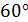 :
: 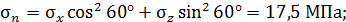
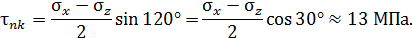
При повороте на угол 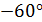 :
: 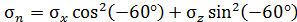
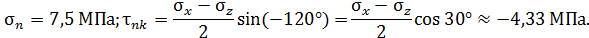
Р.4.5. Верхняя площадка (рис. 13, а) свободна от касательных напряжений. Главные напряжения на этой площадке равны нулю. Два других главных напряжения определим по формулам 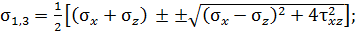 т.к.
т.к. 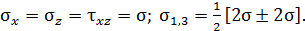
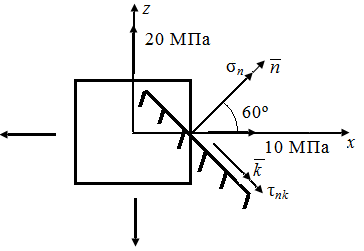
а
| б
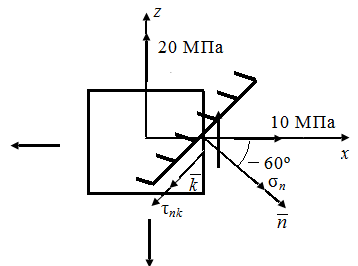
|
| Рис. 46. Схема плоского элемента, выделенного в твердом деформированном теле | |
В соответствии с правилом обозначения главных напряжений: 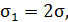
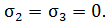 Напряженное состояние - линейное.
Напряженное состояние - линейное.
Боковая площадка (рис. 13, б) свободна от касательных напряжений. Главные напряжения на ней равны нулю. Два других главных напряжения определим по формулам: 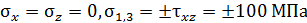 . Напряженное состояние - плоское.
. Напряженное состояние - плоское.
Боковая площадка (рис. 13, в) свободна от касательных напряжений. Это одна из главных площадок, напряжение на которой равно 100 МПа.
Два других главных напряжения определим при следующих значениях нормальных и касательных напряжений на площадках: 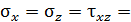
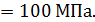
Одно из главных напряжений равно 200 Па, а другое равно нулю. В соответствии с правилом обозначения главных напряжений 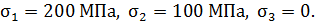 Напряженное состояние - плоское.
Напряженное состояние - плоское.
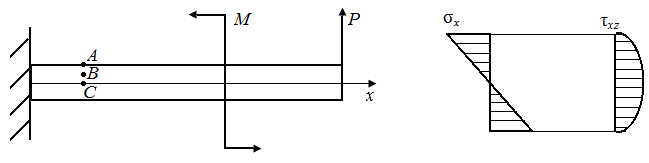
Р.4.6. Эпюры напряжений в поперечном сечении стержня в окрестностях точек А, В, С имеют вид, представленный на рис. 47, а.
В окрестностях точек выделим элементарные параллелепипеды, на гранях которых представим напряжения в окрестностях точек А (рис. 47, в), В (рис. 47, г), С (рис. 47, д). Одна из граней каждого параллелепипеда совпадает с поперечным сечением.
| а б
| ||
в
| г
| д
|
| Рис. 47. Схема нагруженного стержня (а), эпюры нормального и касательного напряжений (б), схемы прямоугольных параллелепипедов, вырезанных из нагруженного стержня (в-д) | ||
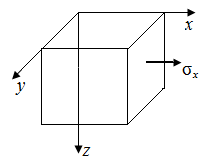
Точка А (рис. 47, в). Все три грани элементарного параллелепипеда являются главными площадками. На двух гранях напряжения равны нулю, на третьей не равно нулю: 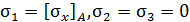 . Напряженное состояние - линейное.
. Напряженное состояние - линейное. 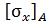 – значение нормального напряжения в точке А.
– значение нормального напряжения в точке А.
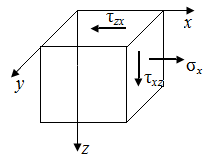
Точка В (рис. 47, г). Напряжения на боковой грани равны нулю. Это одна главная площадка. Напряжения на двух других главных площадках
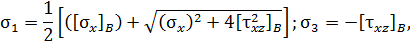
где 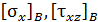 – значения нормального и касательного напряжений в окрестности точки В.
– значения нормального и касательного напряжений в окрестности точки В.
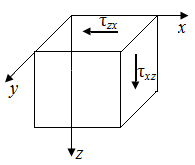
Точка С (рис. 47, д). Напряжения на боковой грани равны нулю. Это одна главная площадка. Напряжения на двух других гранях равны
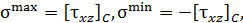
где 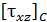 - значение касательного напряжений в окрестности точки С
- значение касательного напряжений в окрестности точки С 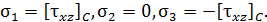 Напряженное состояние - плоское.
Напряженное состояние - плоское.
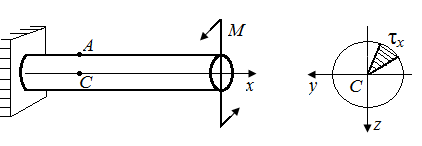
Р.4.7. В окрестности точек А, С (рис. 48) выделим элементарные параллелепипеды. Одна из граней каждого параллелепипеда совпадает с поперечным сечением. Точка С. Напряжения в окрестности точки С равны нулю. 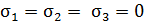 . Напряженное состояние – нулевое.
. Напряженное состояние – нулевое.
Точка А. Напряженное состояние в точке А определим при рассмотрении кубического уравнения. Учитывая, что 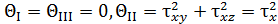 кубическое уравнение принимает вид
кубическое уравнение принимает вид 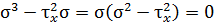 , получаем
, получаем 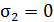 ,
, 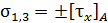 , где
, где 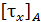 – значение
– значение 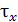 в окрестности точки А. Напряженное состояние – плоское.
в окрестности точки А. Напряженное состояние – плоское.
а б
|
| Рис. 48. Схемы нагруженного стержня (а) и эпюра касательных напряжений (б) |
Р.4.8. На гранях представлены главные напряжения. Эквивалентное напряжение 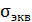 по четвертой теории прочности определяют по следующей формуле
по четвертой теории прочности определяют по следующей формуле 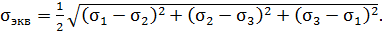
В окрестности точки (рис. 16) действуют главные напряжения 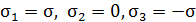 . По формуле
. По формуле 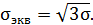
Р.4.9. На гранях представлены главные напряжения. Эквивалентные напряжения по теории наибольших касательных напряжений определяются по формуле 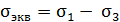 , а по четвертой теории прочности по формуле
, а по четвертой теории прочности по формуле
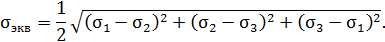
На гранях действуют следующие главные напряжения: а) 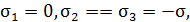 б)
б) 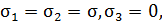 в)
в) 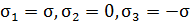 .
.
При расчете по четвертой теории прочности для напряженных состояний а), б), в) напряжения 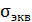 соответственно равны
соответственно равны 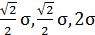 . Самое неблагоприятное напряженное состояние "в".
. Самое неблагоприятное напряженное состояние "в".
При расчете по теории наибольших касательных напряжений, для напряженных состояний а), б), в) напряжения 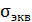 соответственно равны
соответственно равны 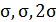 . Самое неблагоприятное напряженное состояние "в".
. Самое неблагоприятное напряженное состояние "в".
Р.4.10. На гранях представлены главные напряжения 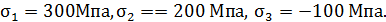 По теории наибольших касательных напряжений, эквивалентное напряжение, определяемое по формуле
По теории наибольших касательных напряжений, эквивалентное напряжение, определяемое по формуле 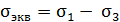 , равно 400 МПа. Это напряжение превышает допускаемое напряжение
, равно 400 МПа. Это напряжение превышает допускаемое напряжение 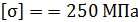 . Деформируемое тело не удовлетворяет условиям прочности.
. Деформируемое тело не удовлетворяет условиям прочности.
Р.4.11. На гранях представлены главные напряжения 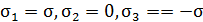 . Главные деформации определяются по формулам
. Главные деформации определяются по формулам 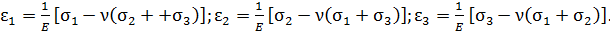
Главные линейные деформации соответственно равны:
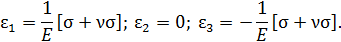
Р.4.12. Первый инвариант тензора напряжений 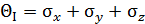 не зависит от пространственной ориентации параллелепипеда.
не зависит от пространственной ориентации параллелепипеда. 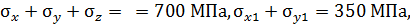 значит
значит 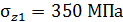 .
.
Р.4.13. Сумма относительных удлинений не зависит от пространственной ориентации элементарного параллелепипеда. Так как 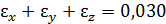 , а
, а 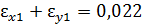 , то
, то 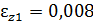 .
.
Р.4.14. Стержень, представленный на рис. 18, испытывает нормальное напряжение 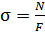 ,
, 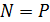 ,
, 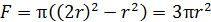 , где
, где 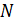 - нормальная сила,
- нормальная сила, 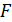 - площадь поперечного сечения стержня. Относительное продольное удлинение стержня
- площадь поперечного сечения стержня. Относительное продольное удлинение стержня 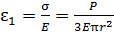 , где
, где 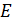 - модуль нормальной упругости материала стержня. Относительное поперечное удлинение стержня
- модуль нормальной упругости материала стержня. Относительное поперечное удлинение стержня 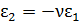 , где
, где 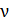 - коэффициент Пуассона:
- коэффициент Пуассона: 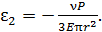 Изменение радиуса стержня
Изменение радиуса стержня 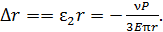
Р.4.15. Коэффициент Пуассона 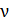 определяется по формуле
определяется по формуле 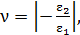 где
где 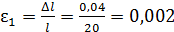 - относительное продольное удлинение стержня;
- относительное продольное удлинение стержня; 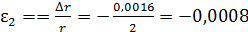 - относительное поперечное сужение стержня. Коэффициент Пуассона равен
- относительное поперечное сужение стержня. Коэффициент Пуассона равен 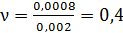 .
.
Дата: 2019-02-25, просмотров: 412.