Р.5.1. На рис. 20 проведем нумерацию грузовых участков слева-направо.
Из условия статического равновесия стержня (рис. 20, а) нормальные силы на первом и втором участках соответственно равны 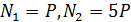 . Нормальное напряжение
. Нормальное напряжение 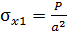 ,
, 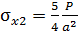 . Максимальное напряжение на втором участке.
. Максимальное напряжение на втором участке.
Нормальные силы и нормальное напряжение в стержне, представленном на рис. 20, б, равны 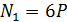 ,
, 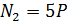 ,
, 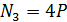 ;
; 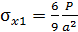 ,
, 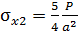 ,
, 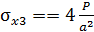 . Максимальное напряжение на третьем участке.
. Максимальное напряжение на третьем участке.
Нормальные силы и нормальное напряжение в стержне, представленном на рис. 20, б, равны 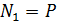 ,
, 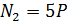 ,
, 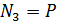 ;
; 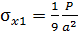 ,
, 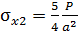 ,
, 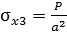 . Максимальное напряжение на втором участке.
. Максимальное напряжение на втором участке.
| а |
|
| б |
|
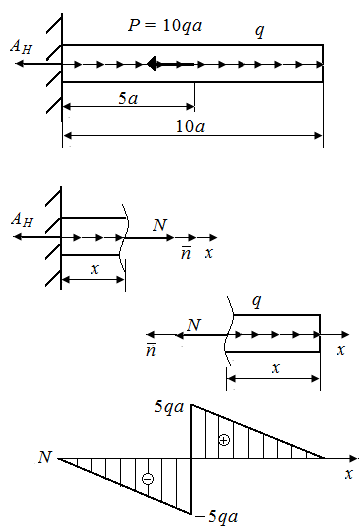
| Рис. 49. Схемы нагруженного стержня и эпюра нормальных напряжений |
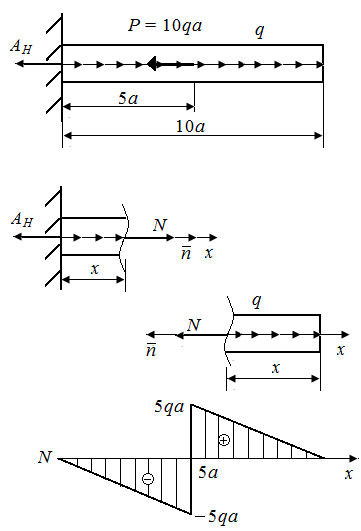
Р.5.2. Определим величину опорной реакции в стержне (рис. 49, а). Из условия статического равновесия 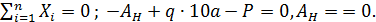 Определим значения нормальных сил на границах грузовых участков и построим эпюр нормальных сил в соответствии с законами изменения
Определим значения нормальных сил на границах грузовых участков и построим эпюр нормальных сил в соответствии с законами изменения 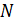 на грузовых участках и значениями
на грузовых участках и значениями 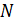 на границе грузовых участков (рис. 49, б).
на границе грузовых участков (рис. 49, б).
Величина экстремального напряжения равна 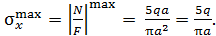
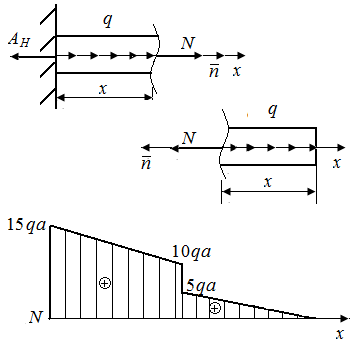
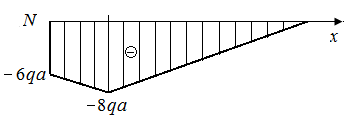
Р.5.3. Определим величину опорной реакции в стержне (рис. 50, а). Из условия статического равновесия 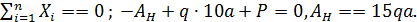 По результатам проведенных вычислений нормальных сил на грузовых участках строим эпюры нормальных (рис. 50, б). Величина экстремального напряжения равна
По результатам проведенных вычислений нормальных сил на грузовых участках строим эпюры нормальных (рис. 50, б). Величина экстремального напряжения равна 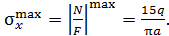
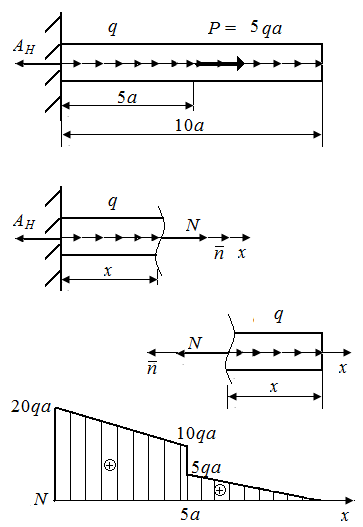
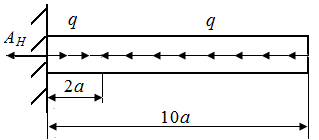
Р.5.4 . Определим величину опорной реакции в стержне (рис. 51, а). Из условия статического равновесия 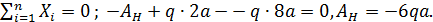 По результатам проведенных вычислений нормальных сил на грузовых участках строим эпюр нормальных сил в соответствии с законами изменения
По результатам проведенных вычислений нормальных сил на грузовых участках строим эпюр нормальных сил в соответствии с законами изменения 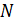 на грузовых участках и значениями
на грузовых участках и значениями 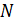 на границе грузовых участков (рис. 51, б). Величина экстремального напряжения равна
на границе грузовых участков (рис. 51, б). Величина экстремального напряжения равна
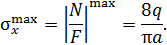
| а | а |
| 
|
| б | б |
| 
|
| Рис. 50. Схемы нагруженного стержня и эпюра нормальных напряжений | Рис. 51. Схемы нагруженного стержня и эпюра нормальных напряжений |
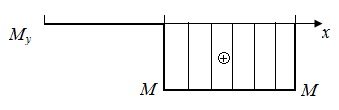
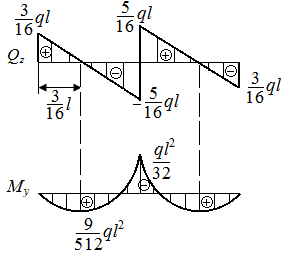
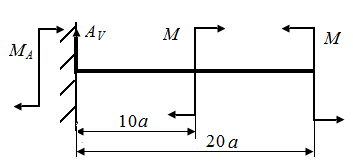
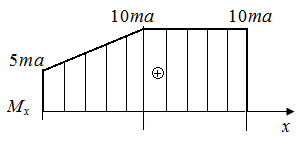
Р.5.5. Опорные реакции при плоском поперечном изгибе стержня (рис. 52, а) 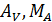 определим рассматривая два условия статического равновесия:
определим рассматривая два условия статического равновесия: 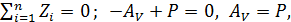
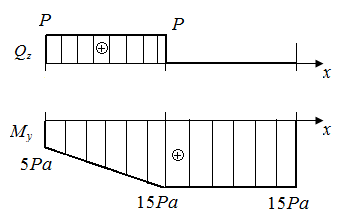
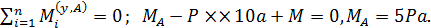 По результатам вычислений
По результатам вычислений 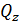 и
и  на границах грузовых участков построены эпюры поперечных сил
на границах грузовых участков построены эпюры поперечных сил 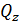 и изгибающих моментов
и изгибающих моментов  (рис. 52, б).
(рис. 52, б).
Экстремальное значение напряжения равно 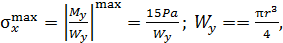 (
( 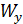 – момент сопротивления круглого сечения при изгибе).
– момент сопротивления круглого сечения при изгибе).
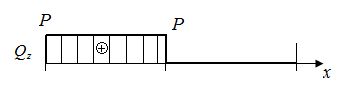
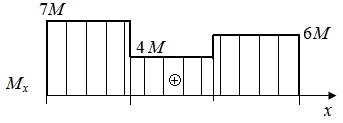
Р.5.6. Определим опорные реакции 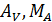 в стержне (рис. 53, а):
в стержне (рис. 53, а): 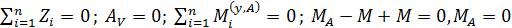 . По результатам вычислений
. По результатам вычислений 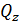 и
и  на границах грузовых участков на рис. 53, в приведена эпюра изгибающих моментов. Экстремальное значение нормального напряжения равно
на границах грузовых участков на рис. 53, в приведена эпюра изгибающих моментов. Экстремальное значение нормального напряжения равно 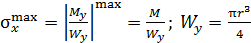 (
( 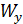 - момент сопротивления круглого сечения при изгибе).
- момент сопротивления круглого сечения при изгибе).
| а | а |

| 
|
| б | б |
|
Рис. 53. Схема стержня и эпюра изгибающих моментов |
| в | |
| |
| Рис. 52. Схема стержня и эпюры поперечных сил и изгибающих моментов |
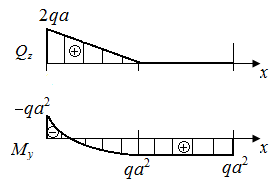
Р.5.7. Определим опорные реакции 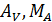 в стержне (рис. 54, а):
в стержне (рис. 54, а): 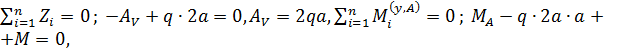
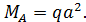 По результатам вычислений
По результатам вычислений 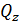 и
и  на границах грузовых участков на рис. 54, в приведена эпюра изгибающих моментов. Экстремальное значение нормального напряжения равно
на границах грузовых участков на рис. 54, в приведена эпюра изгибающих моментов. Экстремальное значение нормального напряжения равно 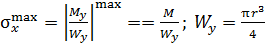 (
( 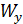 - момент сопротивления круглого сечения при изгибе.
- момент сопротивления круглого сечения при изгибе.
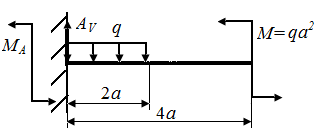
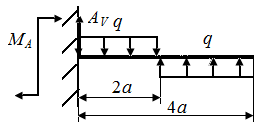
Р.5.8. Определим опорные реакции 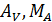 в стержне (рис. 55, а):
в стержне (рис. 55, а): 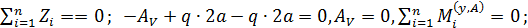
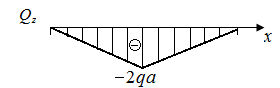
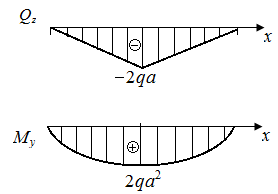
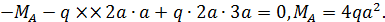 На рис. 55 по результатам вычислений
На рис. 55 по результатам вычислений 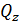 и
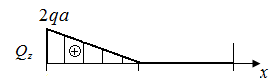
и  на границах грузовых участков приведены эпюры поперечных сил
на границах грузовых участков приведены эпюры поперечных сил 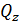 (рис. 55, б) и изгибающих моментов
(рис. 55, б) и изгибающих моментов  (рис. 55, в). Экстремальное значение напряжения равно
(рис. 55, в). Экстремальное значение напряжения равно 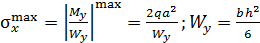 (
( 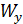 – момент сопротивления прямоугольного сечения при изгибе).
– момент сопротивления прямоугольного сечения при изгибе).
| а | а |
| 
|
| б | б |
| 
|
| в | в |
| 
|
| Рис. 54. Схема стержня и эпюры поперечных сил и изгибающих моментов | Рис. 55. Схема стержня и эпюры поперечных сил и изгибающих моментов |
Р.5.9. Из условия статического равновесия стержня определим опорный момент 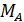 в стержне, представленном на рис. 56, а:
в стержне, представленном на рис. 56, а: 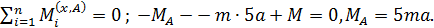 На рис. 56, б приведена эпюра
На рис. 56, б приведена эпюра  , построенная по результатам вычислений значений крутящего момента
, построенная по результатам вычислений значений крутящего момента  на границах грузовых участков. Экстремальное значение напряжения равно
на границах грузовых участков. Экстремальное значение напряжения равно 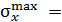
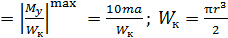 (
( 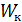 – момент сопротивления при кручении).
– момент сопротивления при кручении).
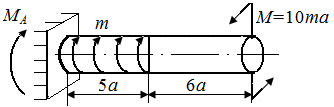
Р.5.10. Из условия статического равновесия стержня определим опорный момент 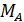 в стержне, представленном на рис. 57, а:
в стержне, представленном на рис. 57, а: 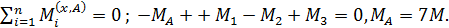 На рис. 57, б приведена эпюра
На рис. 57, б приведена эпюра  , построенная по результатам вычислений значений крутящего момента
, построенная по результатам вычислений значений крутящего момента  на границах грузовых участков. Экстремальное значение напряжения равно
на границах грузовых участков. Экстремальное значение напряжения равно 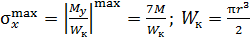 (
( 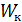 – момент сопротивления при кручении).
– момент сопротивления при кручении).
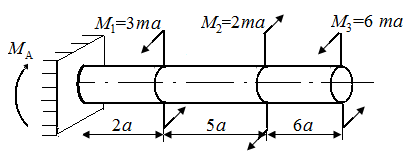
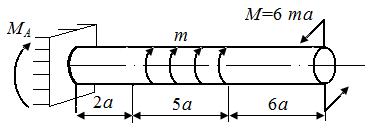
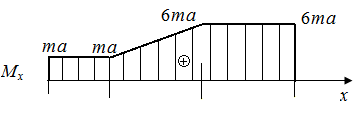
Р.5.11. Из условия статического равновесия стержня определим опорный момент 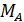 в стержне, представленном на рис. 58, а:
в стержне, представленном на рис. 58, а: 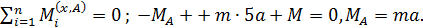 На рис. 58, в приведена эпюра
На рис. 58, в приведена эпюра  , построенная по результатам вычислений значений крутящего момента
, построенная по результатам вычислений значений крутящего момента  на границах грузовых участков.
на границах грузовых участков.
| а | а |
| 
|
| б | б |
| 
|
| Рис. 56. Схема стержня и эпюра крутящих моментов | Рис. 57. Схема стержня и эпюра крутящих моментов |
Экстремальное значение напряжения равно 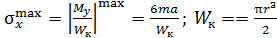 (
( 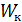 – момент сопротивления при кручении).
– момент сопротивления при кручении).
| а | а |
| 
|
| б | б |
| 
|
| Рис. 58. Схема стержня и эпюра крутящих моментов | Рис. 59. Схема стержня и эпюра крутящих моментов |
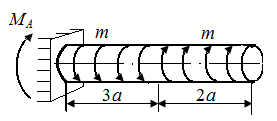
Р.5.12. Из условия статического равновесия стержня определим опорный момент 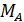 в стержне, представленном на рис. 59, а:
в стержне, представленном на рис. 59, а: 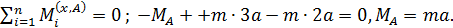
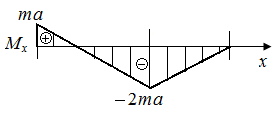
На рис. 59, б приведена эпюра  , построенная по результатам вычислений значений крутящего момента
, построенная по результатам вычислений значений крутящего момента  на границах грузовых участков. Экстремальное значение напряжения равно
на границах грузовых участков. Экстремальное значение напряжения равно 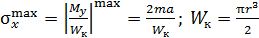 (
( 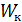 – момент сопротивления при кручении).
– момент сопротивления при кручении).
Расчет перемещений
Р.6.1. В соответствии с формулами, определяющими перемещения при деформации стержней, представленных на рис. 24, при увеличении длины стержня в два раза перемещение u в точке С увеличится в:а) два раза, т. к. 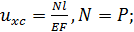 б) три раза, т. к.
б) три раза, т. к.  в) четыре раза, т. к.
в) четыре раза, т. к. 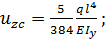 г) два раза, т. к.
г) два раза, т. к. 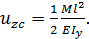
Р.6.2. В соответствии с формулами, определяющими перемещения при деформации стержней, представленных на рис. 25: 1) при увеличении модуля нормальной упругости в два раза перемещение в точке С уменьшатся в два раза;2) при увеличении радиуса круглого поперечного сечения в два раза: а) перемещение 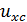 уменьшится в 4 раза, т. к.
уменьшится в 4 раза, т. к. 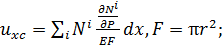 б) перемещение
б) перемещение 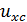 уменьшится в 16 раза, т. к.
уменьшится в 16 раза, т. к. 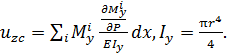
Р.6.3. Перемещение при плоском поперечном изгибе стержня (рис. 25), нагруженного в плоскости xOz, обратно пропорционально осевому моменту 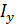 поперечного сечения стержня. Осевой момент инерции
поперечного сечения стержня. Осевой момент инерции 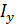 прямоугольного поперечного сечения высотой h и шириной b равен
прямоугольного поперечного сечения высотой h и шириной b равен 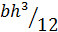 . Увеличение высоты h сечения в два раза увеличивает
. Увеличение высоты h сечения в два раза увеличивает 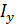 в восемь раз. Значит, в восемь раз уменьшается перемещение. Увеличение ширины поперечного сечения в два раза увеличивает
в восемь раз. Значит, в восемь раз уменьшается перемещение. Увеличение ширины поперечного сечения в два раза увеличивает 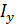 в два раза. Значит, в два раза уменьшится перемещение.
в два раза. Значит, в два раза уменьшится перемещение.
Р.6.4. В соответствии с формулой, определяющей угол поворота 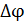 при кручении стержня, представленного на рис. 26,
при кручении стержня, представленного на рис. 26, 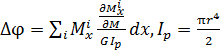 (
( 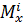 – выражение для крутящего момента на i–ом грузовом участке; M – внешний момент, приложенный в сечении, где определяется перемещение;
– выражение для крутящего момента на i–ом грузовом участке; M – внешний момент, приложенный в сечении, где определяется перемещение;  – модуль нормальной упругости;
– модуль нормальной упругости; 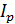 – полярный момент инерции;
– полярный момент инерции; 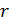 – радиус поперечного сечения).
– радиус поперечного сечения).
При увеличении модуля упругости при сдвиге  в два раза, угол поворота уменьшится в два раза. При увеличении радиуса поперечного сечения в два раза, полярный момент инерции
в два раза, угол поворота уменьшится в два раза. При увеличении радиуса поперечного сечения в два раза, полярный момент инерции 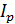 увеличивается в 16 раз. Значит угол поворота уменьшится в 16 раз.
увеличивается в 16 раз. Значит угол поворота уменьшится в 16 раз.
Р.6.5. Перемещение при плоском поперечном изгибе стержня, нагруженного в плоскости xOz, обратно пропорционально осевому моменту инерции 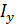 . Осевой момент инерции
. Осевой момент инерции 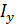 круглого поперечного сечения типа представленного на рис. 27 определяется по формуле
круглого поперечного сечения типа представленного на рис. 27 определяется по формуле 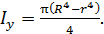 При увеличении внутреннего радиуса
При увеличении внутреннего радиуса 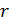 в 1,2 раза, осевой момент инерции уменьшится в 1,07 раза. Значит, перемещение увеличится в 1,07 раза. При увеличении наружного радиуса
в 1,2 раза, осевой момент инерции уменьшится в 1,07 раза. Значит, перемещение увеличится в 1,07 раза. При увеличении наружного радиуса  в 1,2 раза, осевой момент инерции увеличится в 2,15 раз. Значит, перемещение уменьшится в 2,15 раз.
в 1,2 раза, осевой момент инерции увеличится в 2,15 раз. Значит, перемещение уменьшится в 2,15 раз.
Р.6.6. Выражение для осевого момента инерции 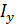 поперечного сечения стержня, представленного на рис. 28, принимает вид
поперечного сечения стержня, представленного на рис. 28, принимает вид 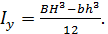 При
При 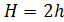 и
и 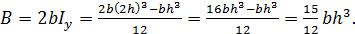 При увеличении
При увеличении 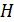 в 1,2 раза
в 1,2 раза  Осевой момент инерции увеличился в 1,8 раз. Значит, перемещение уменьшилось в 1,8 раз. При увеличении
Осевой момент инерции увеличился в 1,8 раз. Значит, перемещение уменьшилось в 1,8 раз. При увеличении 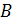 в 1,2 раза
в 1,2 раза 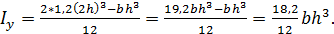
Осевой момент инерции увеличился в 1,21 раз. Значит, перемещение уменьшилось в 1,21 раз. При увеличении 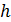 в 1,2 раза
в 1,2 раза 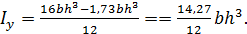 Перемещение увеличилось в 1,2 раза. При увеличении
Перемещение увеличилось в 1,2 раза. При увеличении 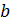 в 1,2 раза
в 1,2 раза 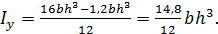 Перемещение увеличилось в 1,01 раз.
Перемещение увеличилось в 1,01 раз.
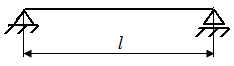
Р.6.7. Из условия статического равновесия при симметричном нагружении стержня (рис. 60) 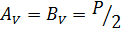 . Уравнение изогнутой линии стержня принимает вид
. Уравнение изогнутой линии стержня принимает вид 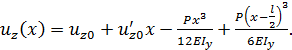 Постоянные
Постоянные 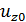 и
и 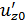 определим из граничных условий: При
определим из граничных условий: При 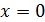 перемещение
перемещение 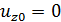 ; При
; При 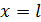 перемещение также равно нулю.
перемещение также равно нулю.
Перемещение 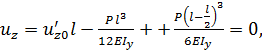 и, следовательно,
и, следовательно,  . Угол поворота в точке А
. Угол поворота в точке А 
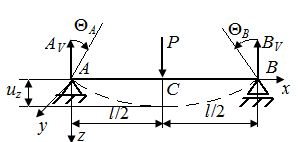 Рис. 60. Симметрично нагруженный стержень
Рис. 60. Симметрично нагруженный стержень
|
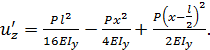 Перемещение в точке С при
Перемещение в точке С при 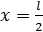 равно
равно 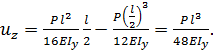 Величина
Величина 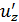 при
при 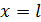 равна
равна 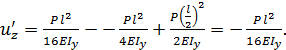
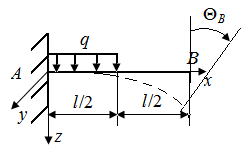 Рис. 61. Стержень, испытывающий плоско-поперечный изгиб
Рис. 61. Стержень, испытывающий плоско-поперечный изгиб
|
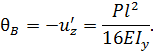
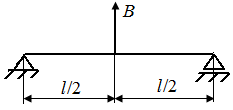
Р.6.8. Из условий равновесия возникающие в заделке стержня (рис. 61) опорная реакция и момент соответственно равны 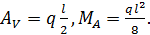
В начале отсчета (точка А) в заделке запрещено перемещение и поворот: 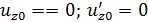 .
.
Уравнения упругой линии и углов поворота принимают вид:
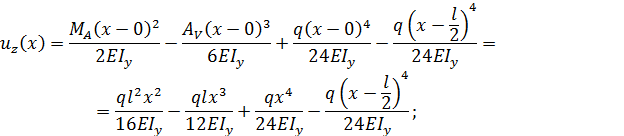
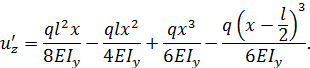
Параметр 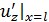 при
при 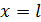 равен
равен 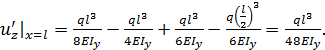 Угол поворота поперечной плоскости, проходящей через точку В
Угол поворота поперечной плоскости, проходящей через точку В
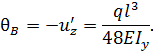
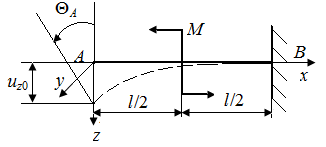 Рис. 62. Нагруженный стержень
Рис. 62. Нагруженный стержень
|
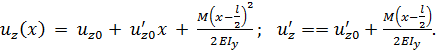
Граничные условия: при 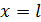 в заделке перемещение и угол поворота запрещены:
в заделке перемещение и угол поворота запрещены: 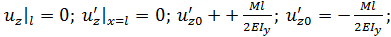
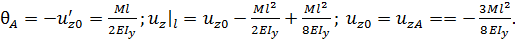
Р.6.10. В стержнях, представленных на рис. 30, на каждый стержень накладывается по четыре связи, а условий статического равновесия, при нагружении стержня в плоскости всего три. Статическую неопределимость можно раскрыть, задав по одному условию, запрещающему перемещение или угол поворота в точке опоры или заделке. Для стержня, представленного на рис. 30, перемещения в точке С или точке В, направленных по оси z , равны нулю: 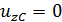 либо
либо 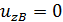 . Перемещение по направлению оси z (рис. 30, б) в точке А
. Перемещение по направлению оси z (рис. 30, б) в точке А 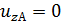 , либо угол поворота относительно оси y в плоскости, проходящей через точку В
, либо угол поворота относительно оси y в плоскости, проходящей через точку В 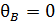 .
.
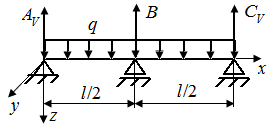
Р.6.11. Раскроем статическую неопределимость (рис. 63, а) методом уравнивания перемещений: 1. Выбираем основную систему (рис. 63, б), которую получаем из заданного стержня с нагрузкой, путем отбрасывания одной лишней связи (связи в точке В); 2. Нагружаем основную систему заданной нагрузкой (рис. 63, в) и определяем перемещение в сечении, где была лишняя связь 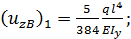 3. Загружаем основную систему реакцией лишней связи (рис. 63, г) и определяем перемещение в том же сечении
3. Загружаем основную систему реакцией лишней связи (рис. 63, г) и определяем перемещение в том же сечении 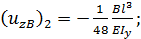 4. Составляем уравнение совместности перемещений
4. Составляем уравнение совместности перемещений 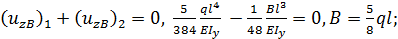
| а | д |
| 
|
| б | е |
| |
| в | |

| |
| г | |
| |
| Рис. 63. Решение статически неопределимой задачи методом уравнения перемещений | |
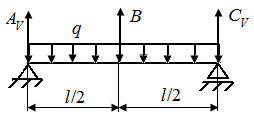
5. Из условий статического равновесия в системе (рис. 63, д) 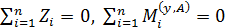 определяем опорные реакции
определяем опорные реакции 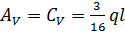 и строим эпюры
и строим эпюры 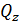 и
и  (рис. 63, е).
(рис. 63, е).
Дата: 2019-02-25, просмотров: 374.