7.1. Как изменятся динамические напряжения в элементе конструкции:    1. Испытывающем растяжение - сжатие (рис. 35, а), если в 4 раза уменьшить его: а) площадь поперечного сечения; б) модуль нормальной упругости,              в) объем; г) радиус круглого поперечного сечения; д) вес груза;                                          2. Испытывающем плоско поперечный изгиб (рис. 35, б), если в 4 раза увеличить его: а) модуль нормаль­ной упругости; б) радиус круглого поперечного сечения; 3. При резкой остановке вращающегося вала (рис. 35, в), если в 4 раза увеличить: а) длину стержня; б) радиус; в) модуль сдвига;            г) объем; д) площадь поперечного сечения?

7.2. Как изменятся нормальные динамические напряжения в стержне, нагруженном в соответствии с рис. 35, а, при увеличении высоты падения груза в 9 раз?

РЕШЕНИЕ ЗАДАЧ

Основные понятия прикладной механики

Р.1.1. Принцип относительной жесткости позволяет при составлении уравнений равновесия рассматривать тело как недеформированное, обладающее теми же геометрическими размерами, которое оно имело до нагружения.

Применение принципа суперпозиции позволяет получить решение как результат наложения частных решений.

Применение принципа Сен-Венана позволяет считать, что если в пределах некоторой области упругого тела приложена система сил, то на расстояниях, существенно превышающих характерные размеры взятой области, напряжения и деформации практически одинаковы для всех статически эквивалентных систем сил.

Р.1.2. Допущение о сплошности материала элемента конструкции позволяет пользоваться методом анализа бесконечно малых (интегрировать, дифференцировать). Оно приемлемо лишь для тел, размеры которых существенно превышают межатомные расстояния.

Допущение однородности материала допускает, что его механические свойства неизменны в пределах рассматриваемой области.

Допущение анизотропности позволяет считать, что физические и механические свойства не зависят от угловой ориентации элемента конструкции.

Р.1.3. Для удобства вычислений главный вектор внутренних сил 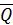 и вектор главного момента  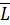раскладывают на составляющие: а) главный вектор сил на нормальную силу  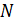и поперечные силы 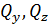; б) вектор главного мо­мента на три пары сил с крутящим моментом  и двумя изгибающими моментами  и .

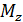Р.1.4. Когда направление внешней нормали к сечению 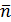 совпадает с направлением оси координат х (левая отсеченная часть стержня), то составляющие внутренних сил  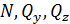положительны, если они направлены в ту же сторону, что и соответствующие координатные оси. Когда внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х (правая отсеченная часть стержня), то составляющие внутренних сил  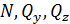будут положительны, если они направлены в стороны, противоположные направлениям соответствующих координатных осей.

Р.1.5. Когда направление внешней нормали к сечению 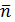совпадает с направлением оси х, моменты  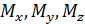считаются положительными, если они действуют против часовой стрелки при рассмотрении с концов соответствующих координатных осей. Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х, то моменты 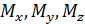будут положительны, если они создают вращение по часовой стрелке при рассмотрении с концов соответствующих координатных осей.

Р.1.6. Углы сдвига в элементарном параллелепипеде – 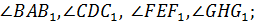 перемещения – .

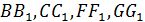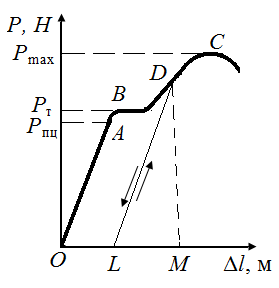
Р.1.7. На рис. 36, а приведена диаграмма растяжения образца из пластичного материала, а на рис. 36, б диаграмма условных напряжений для того же образца. После стадии текучести материала ( 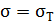) на диаграмме точки С (рис. 36, б) деформация в каждый момент времени складывается из упругой и пластичной. При разгружении образца из точки D линия разгрузки DL параллельна первоначальному участку OA. На рис. 36, а отрезок LM – исчезающее удлинение образца, отрезок OL – остаточное удлинение образца.

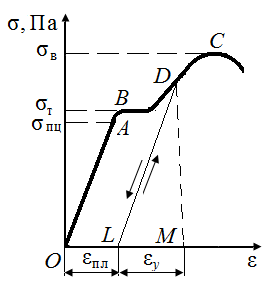
На рис. 36, б отрезок 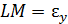 – упругое относительное удлинение, отрезок  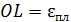– пластическое относительное удлинение. Если нагружать образец снова, напряжение пойдет по прямой LD. Жесткость стержня не изменится, а предел пропорциональности возрастет.

а	б
Рис. 36. Диаграммы растяжения (а) и условных напряжений (б) из пластичного материала

Р.1.8. Внешние силы выражают меру взаимодействия стержня с другими телами, а внутренние силовые факторы 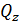 и  – изменение сил межатомного взаимодействия при деформации стержня.

Р.1.9. Опорные реакции – мера взаимодействия между нагруженным стержнем и опорами. Это внешние силы.

Р.1.10. Условия статического равновесия устанавливают связь между проекциями сил 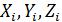 на оси xyz и связь между моментами  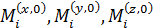относительно осей xyz.

Р.1.11. Стержни, представленные на рис. 5, нагружены в плоскости xOz. Условия статического равновесия определяются тремя уравнениями, которые позволяют определить три неизвестных опорных реакции. На стержень, приведенный на рис. 5, а, накладываются четыре связи. Система статически неопределима. На стержень, приведенный на рис. 5, б, накладываются три связи - система статически определима.

Р.1.12. Необходимо выполнить следующие закрепления стержня (рис. 6): 1) жесткое защемление в плоскости, проходящей через точку А; 2) неподвиж­ная опора, запрещающая перемещение вдоль оси x и z в точке A, и подвижная опора, запрещающая перемещение вдоль оси z в точке B; 3) закрепление, аналогичное закреплению п.2).

Р.1.13. Материал стержня, приведенного на рис. 8: 1) упругий, 2) упруго-пластичный, 3) пластичный.