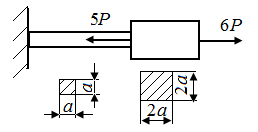
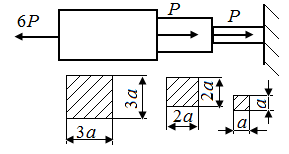
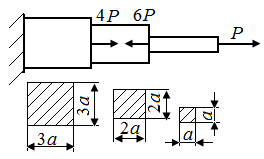
5.1. На рис. 20 (а - в) заданы стержни, нагруженные осевыми силами. На каких участках стержней возникают максимальные нормальные напряжения?

а	б
в	Рис. 20. Схемы стержней, нагруженных осевыми силами

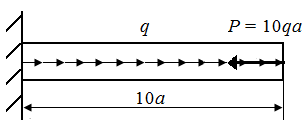
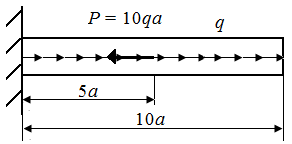
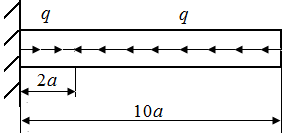
5.2. Определить опасное сечение и величину экстремального значения напряжения в стержнях круглого поперечного сечения радиуса r, нагруженных в соответствии с рис. 21, а – г.

а	б
в	г
Рис. 21. Схемы стержней круглого поперечного сечения

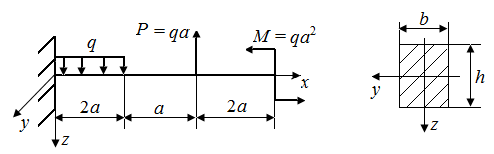
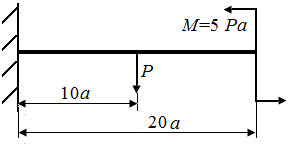
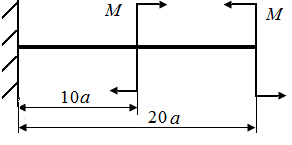
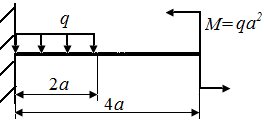
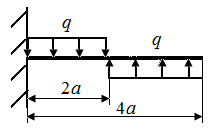
5.3. Определить величины экстремальных значений напряжений в стержнях нагруженных в соответствии с рис. 22, а - г. На рис. 22, а, б стержни круглого поперечного сечения радиуса r.

а	б
в	г
Рис. 22. Схемы стержней, испытывающих плоский поперечный изгиб

На рис. 22, в, г стержни прямоугольного поперечного сечения высотой h и шириной b.

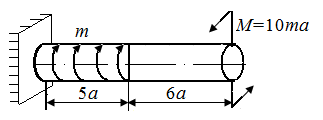
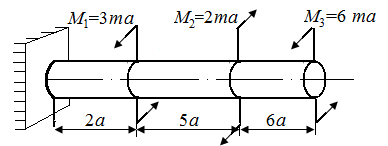
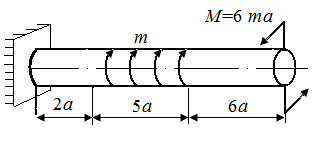
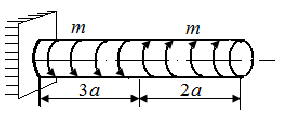
5.4. В стержнях круглого поперечного сечения радиуса r, нагруженных в соответствии с рис. 23, а – г, определить опасное сечение и величину экстре­мального значения напряжения.

а	б
в	г
Рис. 23. Схемы стержней, испытывающих кручение

Расчет перемещений

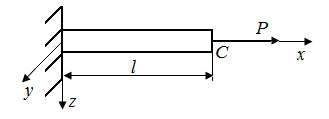
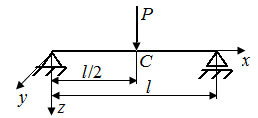
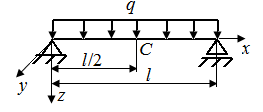
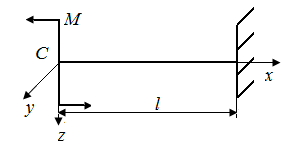
6.1. Как изменятся величины перемещений точек С в стержнях, представ­ленных на рис. 24, а – г, если их длину увеличить в два раза?

а	б
в	г
Рис. 24. Схемы стержней, испытывающих перемещения

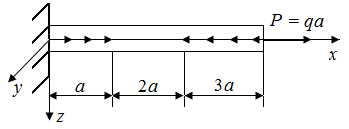
6.2. Как изменятся величины перемещений точек С в стержнях круглого поперечного сечения, представленных на рис. 25, а, б, при увеличении в 2 раза: а) модуля нормальной упругости материала стержня; б) радиуса поперечного сечения?

а	б
Рис. 25. Схемы стержней, испытывающих перемещения

6.3. Как изменится перемещение точки С в представленном на рис. 26, стержне прямоугольного поперечного сечения при увеличении: а) высоты h в два раза; б) ширины b в два раза?

6.4. Как изменится угол поворота стержня круглого поперечного сечения, представленного на рис. 27, при увеличении в два раза: а) модуля упругости при сдвиге G; б) радиуса поперечного сечения r?

6.5. Как изменится перемещение точки С стержня, представленного на рис. 28, при увеличении в 1,2 раза: а) внутреннего радиуса r, б) наружного ра­диуса R? Наружный радиус .

а                                                                                          б

Рис. 27. Схемы стержня, испытывающего кручение (а)  и его поперечного сечения (б)

6.6. Как изменится перемещение точки С стержня, представленного на рис. 29, при увеличении в два раза параметра: а) 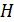; б) h; в) B; г) b? Исходное соотношение параметров .

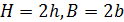а                                                                                 б

Рис. 28. Схемы стержня, испытывающего плоский поперечный изгиб (а) и его поперечного сечения (б)

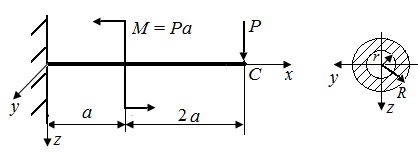
6.7. Определить перемещение в точке и углы поворота в поперечных плоскостях, проходящих через точки А и В стержня, нагруженного в соответ­ствии с рис. 30. Изгибная жесткость стержня .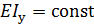

а                                                                      б

Рис. 29. Схемы стержня, испытывающего плоский поперечный изгиб (а) и его поперечного сечения (б)

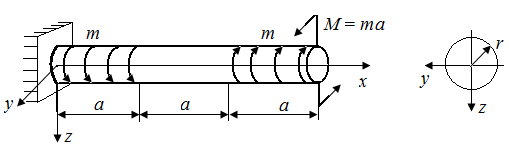
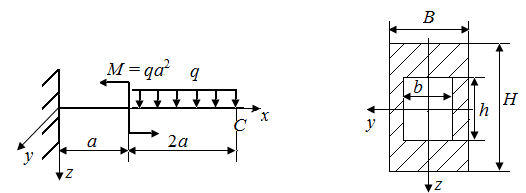
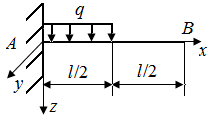
6.8. Определить угол поворота поперечной плоскости, проходящей через точку В стержня, нагруженного в соответствии с рис. 31.

Рис. 30. Схемы стержня, нагруженного сосредоточенной силой	Рис. 31. Схемы стержня, находящегося под действием распределенной нагрузки

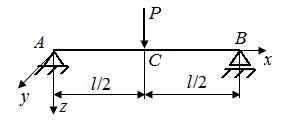
6.9. Определить перемещение в точке А стержня, нагруженного в соответствии с рис. 32.

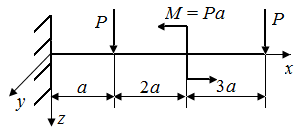
Рис. 32. Схемы стержня, нагруженного сосредоточенным моментом

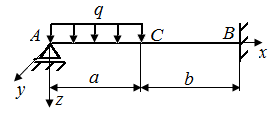
6.10. Какие условия позволяют раскрыть статическую неопределенность в стержнях, закрепленным по схемам рис. 33 (а, б)?

а	б
Рис. 33. Схемы стержней, испытывающих плоский поперечный изгиб

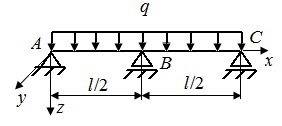
6.11. Раскрыть статическую неопределимость в стержне, представленном на рис. 34. Построить эпюры поперечных сил и изгибающих моментов.

Рис. 34. Схемы стержней, испытывающих плоский поперечный изгиб

а	б
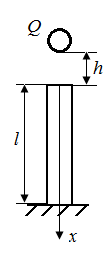
в
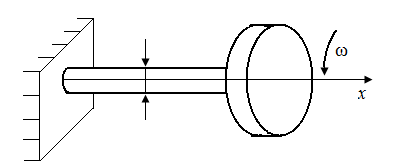
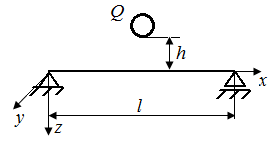
	Рис. 35. Схема стержня, испытывающего динамические нагрузки при сжатии (а), изгибе (б) и при резкой остановке вращающегося вала (в)