4.1. Корни кубического уравнения 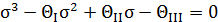 определяют нормальные напряжения, действующие на главных площадках. Почему оно инвариантно (безразлично) к изменению системы координат?
определяют нормальные напряжения, действующие на главных площадках. Почему оно инвариантно (безразлично) к изменению системы координат?
4.2. Как и почему так называют коэффициенты 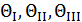 кубического уравнения?
кубического уравнения?
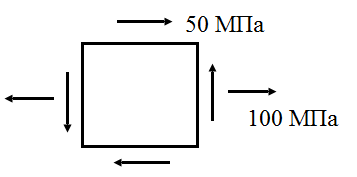
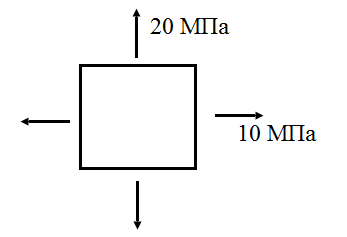
4.3. Для плоского элемента, выделенного в твердом теле, заданы напряжения в соответствии с рис. 11. Определить: а) значения напряжений на площадке, нормаль к которой повернута на угол 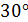 к горизонтальной оси; б) значения напряжений на площадке, нормаль к которой повернута на угол
к горизонтальной оси; б) значения напряжений на площадке, нормаль к которой повернута на угол 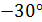 к горизонтальной оси; в) значения главных напряжений; г) положения главных площадок.
к горизонтальной оси; в) значения главных напряжений; г) положения главных площадок.
4.4. Для плоского элемента, выделенного в твердом теле, заданы напряжения в соответствии с рис. 12. Определить значения напряжений: а) на площадке, нормаль к которой повернута на угол 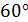 к горизонтальной оси; б) на площадке, нормаль к которой повернута на угол
к горизонтальной оси; б) на площадке, нормаль к которой повернута на угол 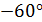 к горизонтальной оси.
к горизонтальной оси.
| 
|
| Рис. 11. Схема плоского элемента, выделенного в твердом теле | Рис. 12. Схема плоского элемента, выделенного в твердом теле |
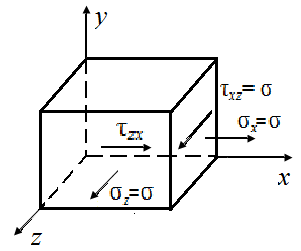
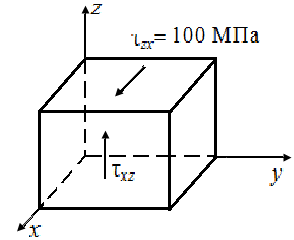
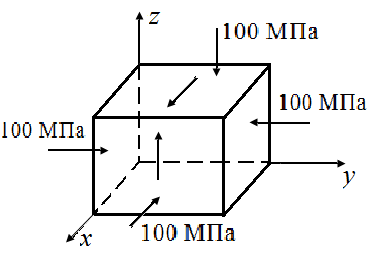
4.5. На гранях элементарного параллелепипеда в форме кубика, вырезанного из деформированного тела, действуют напряжения в соответствии с рис. 13 (а - в).
Определить главные напряжения и характер напряженного состояния: объемное, плоское или линейное?
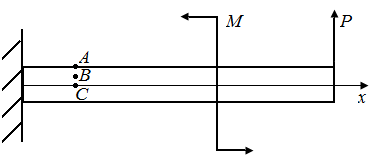
4.6. Стержень на рис. 14 испытывает плоский поперечный изгиб. Определить главные напряжения и напряженное состояние в окрестности точек A, B, C.
| а | б | в |
| 
| 
|
| Рис. 13. Схемы элементарных параллелепипедов, вырезанных из деформированного тела | ||
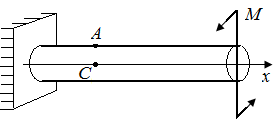
4.7. Стержень на рис. 15 испытывает кручение. Определить главные напряжения и напряженное состояние в окрестности точек A, C.
| 
|
| Рис. 14. Схема стержня, испытывающего плоский поперечный изгиб | Рис. 15. Схема стержня, испытывающего кручение |
|
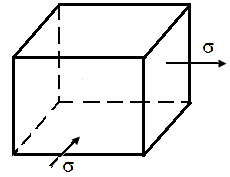
| Рис. 16. Схема элементарного параллелепипеда, вырезанного из деформированного тела |
4.8. На гранях элементарного параллелепипеда в форме кубика, вырезанного из деформированного тела, действуют напряжения в соответствии с рис. 16.
Определить значение эквивалентного напряжения по критерию удельной потенциальной энергии формообразования (четвертая теория прочности).
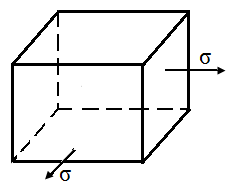
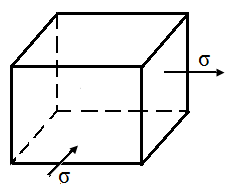
4.9. На рис. 17 приведены элементарные параллелепипеды в форме кубиков, вырезанные в окрестности точек деформированных тел. На гранях кубиков заданы напряжения в соответствии с рис. 17. Определить в каком кубике напряженное состояние самое неблагоприятное: а) по четвертой теории прочности, б) по теории наибольших касательных напряжений.
а

| б
| в
|
| Рис. 17. Схемы элементарных параллелепипедов, вырезанных из деформированного тела | ||
| а | б |
| 
|
| в | г |
| 
|
| Рис. 18. Схемы элементарных параллелепипедов, вырезанных в окрестности точки деформированного тела | |
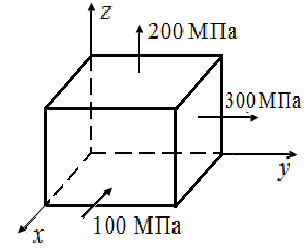
4.10. На рис. 18 приведены схемы элементарных параллелепипедов в форме кубиков, вырезанных в окрестностях точек деформированного тела. На гранях кубиков заданы напряжения.
Для рис 18, а определить по теории наибольших касательных напряжений разрушится тело или нет при таком напряженном состоянии. Допускаемое напряжение материала 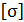 = 250 МПа.
= 250 МПа.
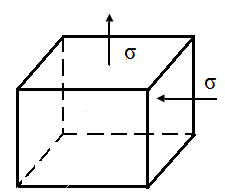
4.11. На рис. 18, б известны значения нормального напряжения σ, модуля нормальной упругости E и коэффициента Пуассона 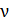 . Определить главные линейные деформации.
. Определить главные линейные деформации.
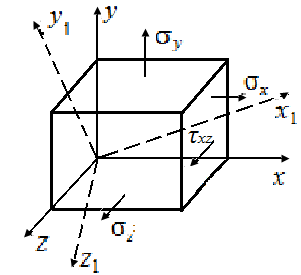
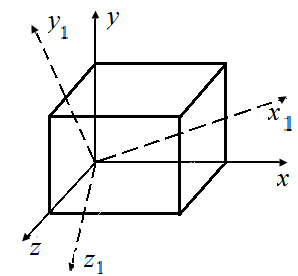
4.12. На рис. 18, в на гранях кубика в системе координат 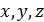 заданы напряжения
заданы напряжения 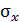 = 200 МПа,
= 200 МПа, 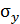 = 100 МПа,
= 100 МПа, 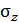 = 400 МПа,
= 400 МПа, 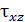 = 50 МПа. В повернутой относительно системы координат
= 50 МПа. В повернутой относительно системы координат 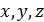 системе
системе 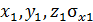 = = 150 МПа,
= = 150 МПа, 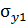 = 200 МПа,
= 200 МПа, 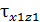 = 50 МПа. Определить значение
= 50 МПа. Определить значение 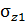 .
.
4.13. На рис. 18, г грани ориентированы по нормали к осям системы координат 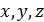 . Относительные удлинения в окрестности точки равны
. Относительные удлинения в окрестности точки равны 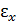 = = 0,005,
= = 0,005, 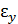 = 0,012,
= 0,012, 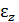 = 0,013. Известны относительные удлинения
= 0,013. Известны относительные удлинения 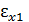 = 0,005,
= 0,005, 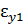 = 0,012 для другой пространственной ориентации
= 0,012 для другой пространственной ориентации 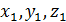 . Определить значение линейной деформации
. Определить значение линейной деформации 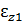 .
.
| а | б |
|
| |
| Рис. 19. Схема стержня испытывающего растяжение | |
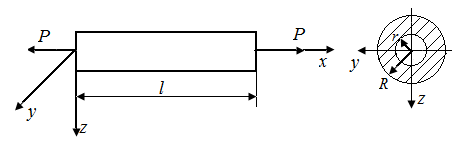
4.14. Определить изменение радиуса r после деформации стержня, представленного на рис. 19, а.
Заданы: сила 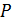 , длина l, радиусы поперечного сечения r и
, длина l, радиусы поперечного сечения r и 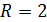 , модуль нормальной упругости стержня E и коэффициент Пуассона
, модуль нормальной упругости стержня E и коэффициент Пуассона 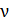 (рис. 19).
(рис. 19).
4.15. В стержне круглого поперечного сечения радиуса r = 2 см и длиной l = 20 см, после растяжения длина увеличивается на 0,04 см, а радиус уменьшается на 0,0016 см. Определить коэффициент Пуассона материала стержня.
Дата: 2019-02-25, просмотров: 396.