ЗАДАЧИ ПРИКЛАДНОЙ МЕХАНИКИ
Электронное учебное пособие
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2017
УДК 531/534(07)
ББК ж 12я7
Б 37
Авторы: П. И. Бегун, Е. А. Лебедева, Д. А. Лобачева
Задачи прикладной механики: электронное учеб. пособие. СПб.:
Изд-во СПБГЭТУ «ЛЭТИ», 2017. 86 с.
ISBN978-5-7629-1688-2
Содержит два раздела и приложение: первый раздел с условиями задач и второй с их решениями. Задачи скомпонованы по следующим темам: 1. Основные понятия прикладной механики; 2. Закрепление стержней. Опорные реакции; 3. Определение внутренних усилий в стержнях; 4. Основные уравнения механики твердого деформированного тела; 5. Расчет напряжений и анализ прочности стержней; 6. Расчет перемещений; 7. Определение динамических параметров при ударе. Приложение содержит основные понятия по прикладной механике
Предназначено для бакалавров, обучающихся по направлениям 12.03.04, 12.03.01, 20.03.01.
УДК 531/534(07)
ББК ж 12я7
Б 37
Рецензенты: кафедра 24 СПбГУАП; д-р пед. наук, проф. А. В. Самсонова (НГУ им. П. Ф. Лесгафта, СПб).
Утверждено
редакционно-издательским советом университета
в качестве учебного пособия
ВВЕДЕНИЕ
Пособие содержит два раздела: первый раздел с условиями задач и второй с их решениями. Задачи скомпонованы по следующим темам: 1. Основные понятия прикладной механики; 2. Закрепление стержней. Опорные реакции; 3. Определение внутренних усилий в стержнях; 4. Основные уравнения механики твердого деформированного тела; 5. Расчет напряжений и анализ прочности стержней; 6. Расчет перемещений; 7. Определение динамических параметров при ударе.
Задачи построены так, чтобы при незначительной затрате времени при понимании материала темы, дать правильный ответ на поставленную задачу.
Задачи могут быть использованы при экспресс опросе студентов для выяснения степени усвоения материала. Приведенные решения задач дают возможность студенту проконтролировать свои умения в реализации полученных знаний при самостоятельной работе.
ЗАДАЧИ
Основные понятия прикладной механики
1.1. Какие возможности при решении задач механики дают три принципа: 1) принцип относительной жесткости; 2) принцип суперпозиции; 3) принцип Сен-Венана?
1.2. Какие возможности при решении задач дает введение допущений сплошности, однородности и изотропности материала конструкций?
1.3. На какие составляющие раскладываются приведенные к центру тяжести сечения главный вектор внутренних сил и вектор главного момента внутренних сил. Как их называют?
1.4. Какие правила знаков вводят для составляющих главного вектора внутренних сил?
1.5. Какие правила знаков вводят для составляющих вектора главного момента внутренних сил?
1.6. На рис. 1 показан элементарный прямоугольный параллелепипед и касательные напряжения 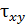 и
и 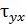 на его гранях. Допускаем, что нижняя грань параллелепипеда жестко закреплена. Указать углы сдвига и перемещения точек.
на его гранях. Допускаем, что нижняя грань параллелепипеда жестко закреплена. Указать углы сдвига и перемещения точек.
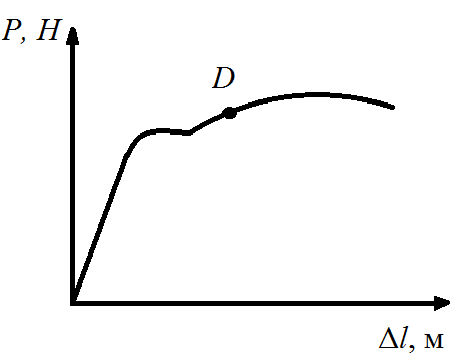
1.7. На рис. 2 приведена диаграмма, полученная при растяжении образца из пластичного материала. Допустим, что аналогичный образец нагрузили до величины, соответствующей точке D и стали разгружать. м
Как определить: 1) величины упругой и пластической деформации; 2) изменятся ли механические характеристики образца?

| 
|
| Рис. 1. Деформированный параллелепипед | Рис. 2. Диаграмма растяжения образца из пластичного материала |
1.8 Какая разница между силовыми факторами 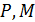 и внутренними силовыми факторами
и внутренними силовыми факторами 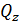 и
и  (рис. 3)?
(рис. 3)?
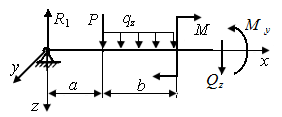
1.9. Опорные реакции (рис. 4) являются внутренними или внешними силами?
| 
|
| Рис. 3. Силовые факторы в сечении нагруженного стержня | Рис. 4. Нагруженный стержень |
1.10. Какие зависимости раскрывают условия статического равновесия?
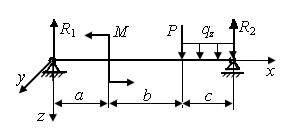
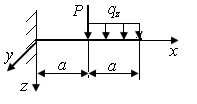
1.11. Достаточно ли условий статического равновесия для определения опорных реакций в стержне, приведенном на рис. 5, а, б?
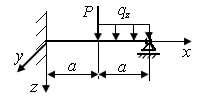
1.12. Как следует закрепить стержень (рис. 6), чтобы: 1) сечение, проходящее через точку А не могло перемещаться вдоль осей x и z и поворачиваться вокруг оси y; 2) сечения, проходящие через точки А и В не могли перемещаться вдоль осей x и z и поворачиваться в плоскости xOz; 3) сечения, проходящее через точку A не могло перемещаться вдоль осей x и z, а сечение, проходящее через точку B - вдоль оси z?
а
| б
|
| Рис. 5. Нагруженный стержень | |
|
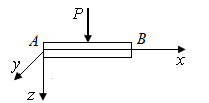
Рис. 7. Стержень нагруженный в плоскости xOz |
| Рис. 6. Незафиксированный стержень | |
1.13. Каким свойством обладает материал стержня (Рис. 7), если после снятия нагрузки: 1) полностью восстанавливает свою первоначальную форму и размеры; 2) частично восстанавливает свою первоначальную форму и размеры; 3) сохраняет ту форму, которую получил при нагружении?
| а | б |
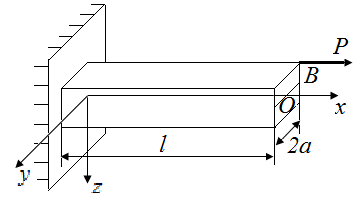
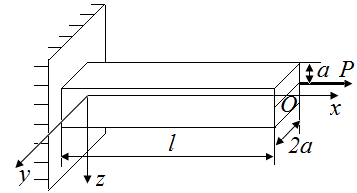
| 
|
| Рис. 8. Схемы стержней, нагруженных вдоль оси х и закрепленных по левому контуру | |
Расчет перемещений
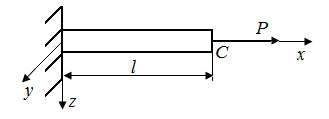
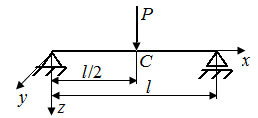
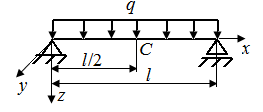
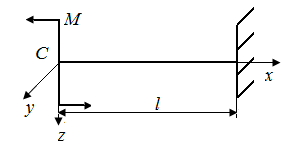
6.1. Как изменятся величины перемещений точек С в стержнях, представленных на рис. 24, а – г, если их длину увеличить в два раза?
| а | б |
| 
|
| в | г |
| 
|
| Рис. 24. Схемы стержней, испытывающих перемещения | |
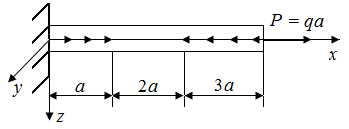
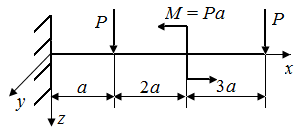
6.2. Как изменятся величины перемещений точек С в стержнях круглого поперечного сечения, представленных на рис. 25, а, б, при увеличении в 2 раза: а) модуля нормальной упругости материала стержня; б) радиуса поперечного сечения?
| а | б |
| 
|
| Рис. 25. Схемы стержней, испытывающих перемещения | |
6.3. Как изменится перемещение точки С в представленном на рис. 26, стержне прямоугольного поперечного сечения при увеличении: а) высоты h в два раза; б) ширины b в два раза?
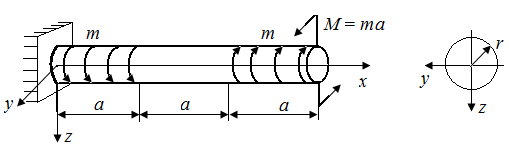
6.4. Как изменится угол поворота стержня круглого поперечного сечения, представленного на рис. 27, при увеличении в два раза: а) модуля упругости при сдвиге G; б) радиуса поперечного сечения r?
| а | б |
|
| |
| Рис. 26. Схемы стержня, испытывающего плоский поперечный изгиб (а) и его поперечного сечения (б) | |
6.5. Как изменится перемещение точки С стержня, представленного на рис. 28, при увеличении в 1,2 раза: а) внутреннего радиуса r, б) наружного радиуса R? Наружный радиус  .
.
а б
|
| Рис. 27. Схемы стержня, испытывающего кручение (а) и его поперечного сечения (б) |
6.6. Как изменится перемещение точки С стержня, представленного на рис. 29, при увеличении в два раза параметра: а) 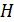 ; б) h; в) B; г) b? Исходное соотношение параметров
; б) h; в) B; г) b? Исходное соотношение параметров 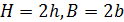 .
.
а б
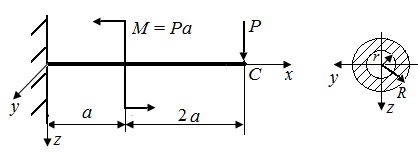
|
| Рис. 28. Схемы стержня, испытывающего плоский поперечный изгиб (а) и его поперечного сечения (б) |
6.7. Определить перемещение в точке и углы поворота в поперечных плоскостях, проходящих через точки А и В стержня, нагруженного в соответствии с рис. 30. Изгибная жесткость стержня 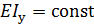 .
.
а б
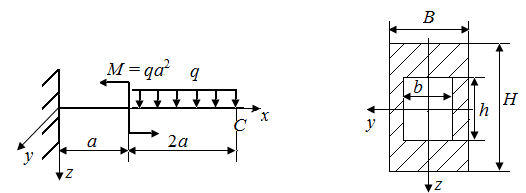
|
| Рис. 29. Схемы стержня, испытывающего плоский поперечный изгиб (а) и его поперечного сечения (б) |
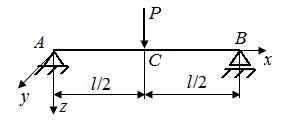
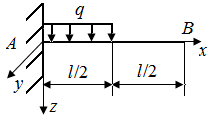
6.8. Определить угол поворота поперечной плоскости, проходящей через точку В стержня, нагруженного в соответствии с рис. 31.
| 
|
| Рис. 30. Схемы стержня, нагруженного сосредоточенной силой | Рис. 31. Схемы стержня, находящегося под действием распределенной нагрузки |
6.9. Определить перемещение в точке А стержня, нагруженного в соответствии с рис. 32.

|
| Рис. 32. Схемы стержня, нагруженного сосредоточенным моментом |
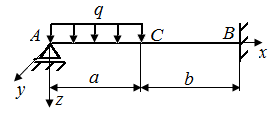
6.10. Какие условия позволяют раскрыть статическую неопределенность в стержнях, закрепленным по схемам рис. 33 (а, б)?
| а | б |

| 
|
| Рис. 33. Схемы стержней, испытывающих плоский поперечный изгиб | |
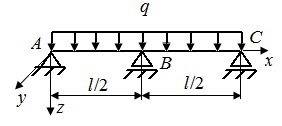
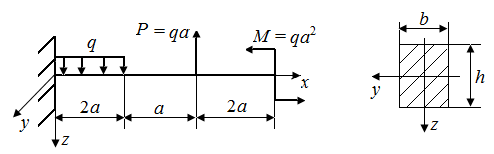
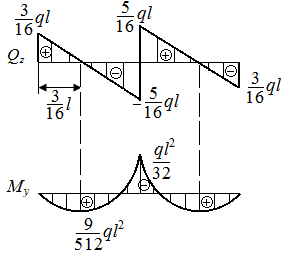
6.11. Раскрыть статическую неопределимость в стержне, представленном на рис. 34. Построить эпюры поперечных сил и изгибающих моментов.
|
| Рис. 34. Схемы стержней, испытывающих плоский поперечный изгиб |
| а | б |
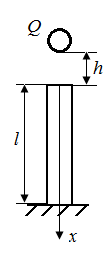
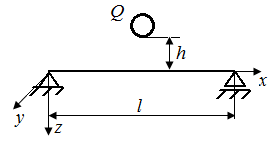
| 
|
| в | |
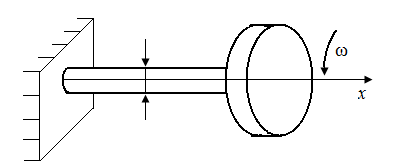
| Рис. 35. Схема стержня, испытывающего динамические нагрузки при сжатии (а), изгибе (б) и при резкой остановке вращающегося вала (в) |
РЕШЕНИЕ ЗАДАЧ
Основные понятия прикладной механики
Р.1.1. Принцип относительной жесткости позволяет при составлении уравнений равновесия рассматривать тело как недеформированное, обладающее теми же геометрическими размерами, которое оно имело до нагружения.
Применение принципа суперпозиции позволяет получить решение как результат наложения частных решений.
Применение принципа Сен-Венана позволяет считать, что если в пределах некоторой области упругого тела приложена система сил, то на расстояниях, существенно превышающих характерные размеры взятой области, напряжения и деформации практически одинаковы для всех статически эквивалентных систем сил.
Р.1.2. Допущение о сплошности материала элемента конструкции позволяет пользоваться методом анализа бесконечно малых (интегрировать, дифференцировать). Оно приемлемо лишь для тел, размеры которых существенно превышают межатомные расстояния.
Допущение однородности материала допускает, что его механические свойства неизменны в пределах рассматриваемой области.
Допущение анизотропности позволяет считать, что физические и механические свойства не зависят от угловой ориентации элемента конструкции.
Р.1.3. Для удобства вычислений главный вектор внутренних сил 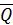 и вектор главного момента
и вектор главного момента 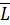 раскладывают на составляющие: а) главный вектор сил на нормальную силу
раскладывают на составляющие: а) главный вектор сил на нормальную силу 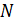 и поперечные силы
и поперечные силы 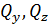 ; б) вектор главного момента на три пары сил с крутящим моментом
; б) вектор главного момента на три пары сил с крутящим моментом  и двумя изгибающими моментами
и двумя изгибающими моментами  и
и 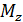 .
.
Р.1.4. Когда направление внешней нормали к сечению 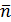 совпадает с направлением оси координат х (левая отсеченная часть стержня), то составляющие внутренних сил
совпадает с направлением оси координат х (левая отсеченная часть стержня), то составляющие внутренних сил 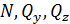 положительны, если они направлены в ту же сторону, что и соответствующие координатные оси. Когда внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х (правая отсеченная часть стержня), то составляющие внутренних сил
положительны, если они направлены в ту же сторону, что и соответствующие координатные оси. Когда внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х (правая отсеченная часть стержня), то составляющие внутренних сил 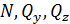 будут положительны, если они направлены в стороны, противоположные направлениям соответствующих координатных осей.
будут положительны, если они направлены в стороны, противоположные направлениям соответствующих координатных осей.
Р.1.5. Когда направление внешней нормали к сечению 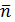 совпадает с направлением оси х, моменты
совпадает с направлением оси х, моменты 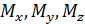 считаются положительными, если они действуют против часовой стрелки при рассмотрении с концов соответствующих координатных осей. Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х, то моменты
считаются положительными, если они действуют против часовой стрелки при рассмотрении с концов соответствующих координатных осей. Если внешняя нормаль к сечению направлена в сторону, противоположную направлению оси х, то моменты 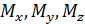 будут положительны, если они создают вращение по часовой стрелке при рассмотрении с концов соответствующих координатных осей.
будут положительны, если они создают вращение по часовой стрелке при рассмотрении с концов соответствующих координатных осей.
Р.1.6. Углы сдвига в элементарном параллелепипеде – 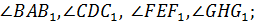 перемещения –
перемещения – 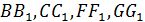 .
.
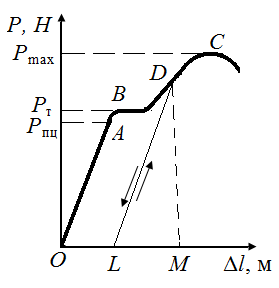
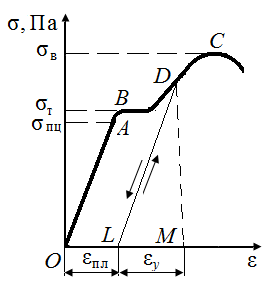
Р.1.7. На рис. 36, а приведена диаграмма растяжения образца из пластичного материала, а на рис. 36, б диаграмма условных напряжений для того же образца. После стадии текучести материала ( 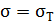 ) на диаграмме точки С (рис. 36, б) деформация в каждый момент времени складывается из упругой и пластичной. При разгружении образца из точки D линия разгрузки DL параллельна первоначальному участку OA. На рис. 36, а отрезок LM – исчезающее удлинение образца, отрезок OL – остаточное удлинение образца.
) на диаграмме точки С (рис. 36, б) деформация в каждый момент времени складывается из упругой и пластичной. При разгружении образца из точки D линия разгрузки DL параллельна первоначальному участку OA. На рис. 36, а отрезок LM – исчезающее удлинение образца, отрезок OL – остаточное удлинение образца.
На рис. 36, б отрезок 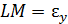 – упругое относительное удлинение, отрезок
– упругое относительное удлинение, отрезок 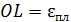 – пластическое относительное удлинение. Если нагружать образец снова, напряжение пойдет по прямой LD. Жесткость стержня не изменится, а предел пропорциональности возрастет.
– пластическое относительное удлинение. Если нагружать образец снова, напряжение пойдет по прямой LD. Жесткость стержня не изменится, а предел пропорциональности возрастет.
а
| б
|
| Рис. 36. Диаграммы растяжения (а) и условных напряжений (б) из пластичного материала | |
Р.1.8. Внешние силы выражают меру взаимодействия стержня с другими телами, а внутренние силовые факторы 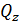 и
и  – изменение сил межатомного взаимодействия при деформации стержня.
– изменение сил межатомного взаимодействия при деформации стержня.
Р.1.9. Опорные реакции – мера взаимодействия между нагруженным стержнем и опорами. Это внешние силы.
Р.1.10. Условия статического равновесия устанавливают связь между проекциями сил 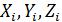 на оси xyz и связь между моментами
на оси xyz и связь между моментами 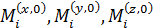 относительно осей xyz.
относительно осей xyz.
Р.1.11. Стержни, представленные на рис. 5, нагружены в плоскости xOz. Условия статического равновесия определяются тремя уравнениями, которые позволяют определить три неизвестных опорных реакции. На стержень, приведенный на рис. 5, а, накладываются четыре связи. Система статически неопределима. На стержень, приведенный на рис. 5, б, накладываются три связи - система статически определима.
Р.1.12. Необходимо выполнить следующие закрепления стержня (рис. 6): 1) жесткое защемление в плоскости, проходящей через точку А; 2) неподвижная опора, запрещающая перемещение вдоль оси x и z в точке A, и подвижная опора, запрещающая перемещение вдоль оси z в точке B; 3) закрепление, аналогичное закреплению п.2).
Р.1.13. Материал стержня, приведенного на рис. 8: 1) упругий, 2) упруго-пластичный, 3) пластичный.
Расчет перемещений
Р.6.1. В соответствии с формулами, определяющими перемещения при деформации стержней, представленных на рис. 24, при увеличении длины стержня в два раза перемещение u в точке С увеличится в:а) два раза, т. к. 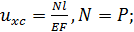 б) три раза, т. к.
б) три раза, т. к.  в) четыре раза, т. к.
в) четыре раза, т. к. 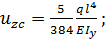 г) два раза, т. к.
г) два раза, т. к. 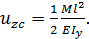
Р.6.2. В соответствии с формулами, определяющими перемещения при деформации стержней, представленных на рис. 25: 1) при увеличении модуля нормальной упругости в два раза перемещение в точке С уменьшатся в два раза;2) при увеличении радиуса круглого поперечного сечения в два раза: а) перемещение 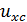 уменьшится в 4 раза, т. к.
уменьшится в 4 раза, т. к. 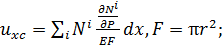 б) перемещение
б) перемещение 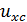 уменьшится в 16 раза, т. к.
уменьшится в 16 раза, т. к. 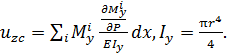
Р.6.3. Перемещение при плоском поперечном изгибе стержня (рис. 25), нагруженного в плоскости xOz, обратно пропорционально осевому моменту 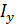 поперечного сечения стержня. Осевой момент инерции
поперечного сечения стержня. Осевой момент инерции 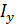 прямоугольного поперечного сечения высотой h и шириной b равен
прямоугольного поперечного сечения высотой h и шириной b равен 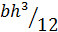 . Увеличение высоты h сечения в два раза увеличивает
. Увеличение высоты h сечения в два раза увеличивает 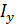 в восемь раз. Значит, в восемь раз уменьшается перемещение. Увеличение ширины поперечного сечения в два раза увеличивает
в восемь раз. Значит, в восемь раз уменьшается перемещение. Увеличение ширины поперечного сечения в два раза увеличивает 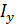 в два раза. Значит, в два раза уменьшится перемещение.
в два раза. Значит, в два раза уменьшится перемещение.
Р.6.4. В соответствии с формулой, определяющей угол поворота 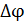 при кручении стержня, представленного на рис. 26,
при кручении стержня, представленного на рис. 26, 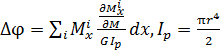 (
( 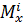 – выражение для крутящего момента на i–ом грузовом участке; M – внешний момент, приложенный в сечении, где определяется перемещение;
– выражение для крутящего момента на i–ом грузовом участке; M – внешний момент, приложенный в сечении, где определяется перемещение;  – модуль нормальной упругости;
– модуль нормальной упругости; 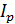 – полярный момент инерции;
– полярный момент инерции; 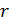 – радиус поперечного сечения).
– радиус поперечного сечения).
При увеличении модуля упругости при сдвиге  в два раза, угол поворота уменьшится в два раза. При увеличении радиуса поперечного сечения в два раза, полярный момент инерции
в два раза, угол поворота уменьшится в два раза. При увеличении радиуса поперечного сечения в два раза, полярный момент инерции 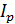 увеличивается в 16 раз. Значит угол поворота уменьшится в 16 раз.
увеличивается в 16 раз. Значит угол поворота уменьшится в 16 раз.
Р.6.5. Перемещение при плоском поперечном изгибе стержня, нагруженного в плоскости xOz, обратно пропорционально осевому моменту инерции 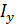 . Осевой момент инерции
. Осевой момент инерции 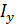 круглого поперечного сечения типа представленного на рис. 27 определяется по формуле
круглого поперечного сечения типа представленного на рис. 27 определяется по формуле 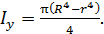 При увеличении внутреннего радиуса
При увеличении внутреннего радиуса 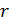 в 1,2 раза, осевой момент инерции уменьшится в 1,07 раза. Значит, перемещение увеличится в 1,07 раза. При увеличении наружного радиуса
в 1,2 раза, осевой момент инерции уменьшится в 1,07 раза. Значит, перемещение увеличится в 1,07 раза. При увеличении наружного радиуса  в 1,2 раза, осевой момент инерции увеличится в 2,15 раз. Значит, перемещение уменьшится в 2,15 раз.
в 1,2 раза, осевой момент инерции увеличится в 2,15 раз. Значит, перемещение уменьшится в 2,15 раз.
Р.6.6. Выражение для осевого момента инерции 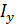 поперечного сечения стержня, представленного на рис. 28, принимает вид
поперечного сечения стержня, представленного на рис. 28, принимает вид 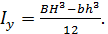 При
При 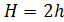 и
и 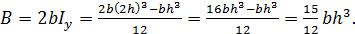 При увеличении
При увеличении 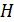 в 1,2 раза
в 1,2 раза  Осевой момент инерции увеличился в 1,8 раз. Значит, перемещение уменьшилось в 1,8 раз. При увеличении
Осевой момент инерции увеличился в 1,8 раз. Значит, перемещение уменьшилось в 1,8 раз. При увеличении 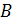 в 1,2 раза
в 1,2 раза 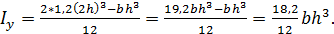
Осевой момент инерции увеличился в 1,21 раз. Значит, перемещение уменьшилось в 1,21 раз. При увеличении 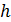 в 1,2 раза
в 1,2 раза 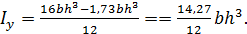 Перемещение увеличилось в 1,2 раза. При увеличении
Перемещение увеличилось в 1,2 раза. При увеличении 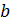 в 1,2 раза
в 1,2 раза 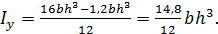 Перемещение увеличилось в 1,01 раз.
Перемещение увеличилось в 1,01 раз.
Р.6.7. Из условия статического равновесия при симметричном нагружении стержня (рис. 60) 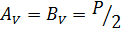 . Уравнение изогнутой линии стержня принимает вид
. Уравнение изогнутой линии стержня принимает вид 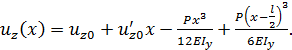 Постоянные
Постоянные 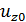 и
и 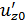 определим из граничных условий: При
определим из граничных условий: При 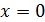 перемещение
перемещение 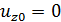 ; При
; При 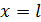 перемещение также равно нулю.
перемещение также равно нулю.
Перемещение 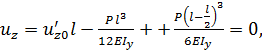 и, следовательно,
и, следовательно,  . Угол поворота в точке А
. Угол поворота в точке А 
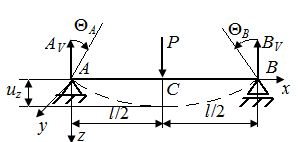 Рис. 60. Симметрично нагруженный стержень
Рис. 60. Симметрично нагруженный стержень
|
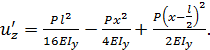 Перемещение в точке С при
Перемещение в точке С при 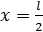 равно
равно 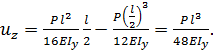 Величина
Величина 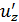 при
при 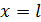 равна
равна 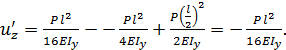
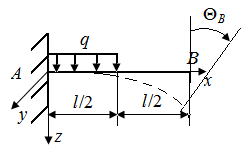 Рис. 61. Стержень, испытывающий плоско-поперечный изгиб
Рис. 61. Стержень, испытывающий плоско-поперечный изгиб
|
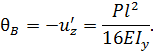
Р.6.8. Из условий равновесия возникающие в заделке стержня (рис. 61) опорная реакция и момент соответственно равны 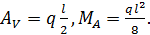
В начале отсчета (точка А) в заделке запрещено перемещение и поворот: 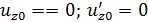 .
.
Уравнения упругой линии и углов поворота принимают вид:
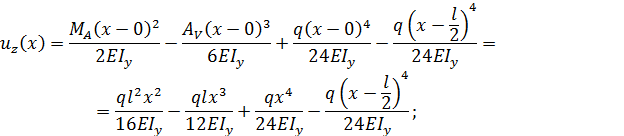
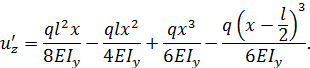
Параметр 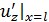 при
при 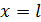 равен
равен 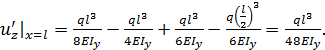 Угол поворота поперечной плоскости, проходящей через точку В
Угол поворота поперечной плоскости, проходящей через точку В
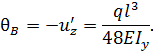
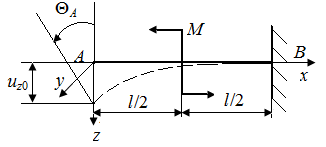 Рис. 62. Нагруженный стержень
Рис. 62. Нагруженный стержень
|
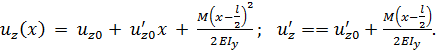
Граничные условия: при 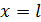 в заделке перемещение и угол поворота запрещены:
в заделке перемещение и угол поворота запрещены: 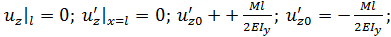
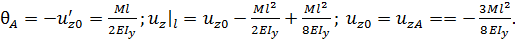
Р.6.10. В стержнях, представленных на рис. 30, на каждый стержень накладывается по четыре связи, а условий статического равновесия, при нагружении стержня в плоскости всего три. Статическую неопределимость можно раскрыть, задав по одному условию, запрещающему перемещение или угол поворота в точке опоры или заделке. Для стержня, представленного на рис. 30, перемещения в точке С или точке В, направленных по оси z , равны нулю: 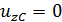 либо
либо 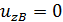 . Перемещение по направлению оси z (рис. 30, б) в точке А
. Перемещение по направлению оси z (рис. 30, б) в точке А 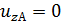 , либо угол поворота относительно оси y в плоскости, проходящей через точку В
, либо угол поворота относительно оси y в плоскости, проходящей через точку В 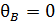 .
.
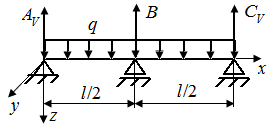
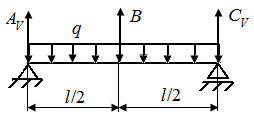
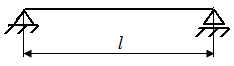
Р.6.11. Раскроем статическую неопределимость (рис. 63, а) методом уравнивания перемещений: 1. Выбираем основную систему (рис. 63, б), которую получаем из заданного стержня с нагрузкой, путем отбрасывания одной лишней связи (связи в точке В); 2. Нагружаем основную систему заданной нагрузкой (рис. 63, в) и определяем перемещение в сечении, где была лишняя связь 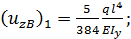 3. Загружаем основную систему реакцией лишней связи (рис. 63, г) и определяем перемещение в том же сечении
3. Загружаем основную систему реакцией лишней связи (рис. 63, г) и определяем перемещение в том же сечении 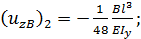 4. Составляем уравнение совместности перемещений
4. Составляем уравнение совместности перемещений 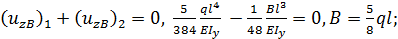
| а | д |
| 
|
| б | е |
| |
| в | |

| |
| г | |
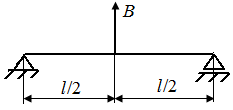
| |
| Рис. 63. Решение статически неопределимой задачи методом уравнения перемещений | |
5. Из условий статического равновесия в системе (рис. 63, д) 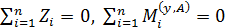 определяем опорные реакции
определяем опорные реакции 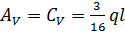 и строим эпюры
и строим эпюры 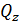 и
и  (рис. 63, е).
(рис. 63, е).
ПРИЛОЖЕНИЕ
П1. Основные понятия прикладной механики
Внешняя сила – мера взаимодействия физических объектов. Если какое-либо тело рассматривают изолированно от окружающих его тел, то действие последних заменяют внешними силами.
Деформация – изменение формы и размеров тела в результате внешнего воздействия. Деформацию считают упругой, если она исчезает после устранения вызвавшей ее силы. В противном случае, деформацию называют остаточной.
Упругость – свойство тела проявлять упругую деформацию.
Пластичность – свойство тела проявлять остаточную деформацию.
Прочность – способность конструкции или отдельных ее элементов выдерживать заданную нагрузку, не разрушаясь.
Жесткость – способность конструкции сопротивляться образованию деформаций.
Устойчивость – способность конструкции противостоять воздействиям, стремящимся вывести ее из исходного состояния равновесия.
По времени действия внешние силы разделяют на постоянные, действующие все время существования изделия, и временные, действующие лишь в течение некоторого промежутка времени.
По характеру действия внешние силы разделяют на статические и динамические. Статические силы сообщают телу малые ускорения, которыми можно пренебречь при исследовании. Динамические силы связаны с возникновением значительных ускорений, которыми пренебрегать нельзя.
Объемные силы распределены по всему объему, занятому телом. Единица объемной силы – ньютон на кубический метр (Н/м3). Рассмотрим некоторое тело (рис. П1.1). Выделим в нем элементарный объем 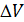 , на который действует объемная сила
, на который действует объемная сила 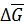 . Среднее значение этой силы находим по формуле
. Среднее значение этой силы находим по формуле
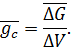
Значение объемной силы в окрестности точки тела равно
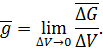
Объемную силу можно разложить по координатным осям х, у, z на составляющие 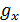 ,
,  ,
, 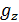 .
.
|
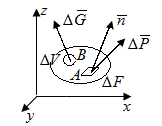
Рис. П1.1. Поверхностная 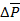 и объемная и объемная 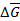 силы, действующие на элементарных участках твердого тела силы, действующие на элементарных участках твердого тела
|
Поверхностные силы распределены по поверхности. Единица поверхностной силы – ньютон на квадратный метр (Н/м2). Выделим в некотором теле на его поверхности элементарную площадку 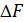 (рис. П1.1). Обозначим через
(рис. П1.1). Обозначим через 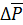 поверхностную силу, действующую на данной элементарной площадке. Среднее значение поверхностной силы определяется по формуле
поверхностную силу, действующую на данной элементарной площадке. Среднее значение поверхностной силы определяется по формуле

Значение поверхностной силы в окрестности точки тела определяет выражение
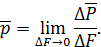
Поверхностную силу можно разложить по координатным осям х, у, z на составляющие 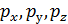 .
.
Если поверхность соприкосновения очень узкая, то можно считать, что сила распределена по линии – распределенная сила. Единица измерения распределенной силы – ньютон на метр (Н/м).
Если площадка, на которой действует поверхностная сила, мала по сравнению с поверхностью всего тела, то поверхностную силу можно считать сосредоточенной в точке тела. Единица сосредоточенной силы - ньютон (Н).
| 
| 
|
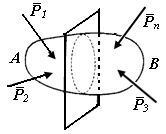
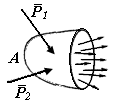
| Рис. П1.2. Внутренние силы в сечении твердого тела | ||
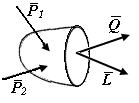
Изменение сил взаимодействия между частицами тела вследствие деформации называют внутренними силами, сопровождающими деформацию. В прикладной механике введено допущение, что тело обладает сплошностью. Для выявления и вычисления внутренних сил применяют метод сечений.
Рассмотрим произвольное тело (рис. П1.2), нагруженное системой сил. Мысленно рассечем его некоторой плоскостью на две части А и В. В точке с обеих сторон сечения будут действовать силы взаимодействия. В зависимости от формы тела и характера приложенных внешних сил интенсивность внутренних сил в различных точках сечения может быть различна. В соответствии с третьим законом Ньютона силы, которые действуют по сечению, принадлежащему части тела А, равны по величине и противоположны по направлению внутренним силам, которые действуют по сечению, принадлежащему части тела В.
Внутренние силы, действующие в сечении, можно привести к одной точке (обычно к центру тяжести сечения), в результате чего на каждой стороне сечения получим главный вектор внутренних сил 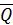 и вектор главного момента внутренних сил
и вектор главного момента внутренних сил 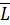 . Для того чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
. Для того чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
|
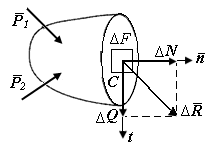
| Рис. П1.3. Элементарная площадка в окрестности точки С |
Рассмотрим сечение А некоторого тела (рис. П1.3). В окрестности точки С выделим элементарную площадку 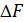 (
( 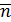 – нормаль к площади сечения). Пусть
– нормаль к площади сечения). Пусть 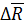 – равнодействующая внутренних сил на площадке,
– равнодействующая внутренних сил на площадке,
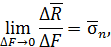
где 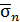 – полное напряжение в окрестности точки С на площадке с нормалью
– полное напряжение в окрестности точки С на площадке с нормалью 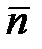 , единица напряжения - Паскаль (Па).
, единица напряжения - Паскаль (Па).
Как равнодействующую внутренних сил 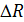 , так и полное напряжение
, так и полное напряжение 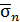 можно разложить на составляющие. Равнодействующую внутренних сил разложим на составляющие
можно разложить на составляющие. Равнодействующую внутренних сил разложим на составляющие 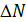 , направленную по нормали к площадке, и
, направленную по нормали к площадке, и 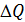 , касательную к площадке. Полное напряжение разложим на нормальное напряжение, действующее в окрестности точки С на площадке с нормалью
, касательную к площадке. Полное напряжение разложим на нормальное напряжение, действующее в окрестности точки С на площадке с нормалью 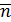 ,
,
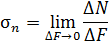
и касательное напряжение, действующее в окрестности точки С на площадке с нормалью 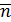 по направлению
по направлению 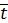 ,
,

Касательное напряжение имеет два индекса – нормали и касательной к площадке.
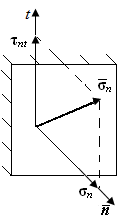
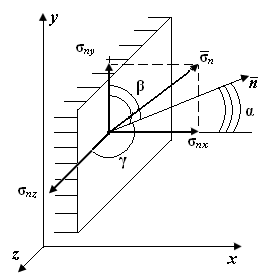
Рассмотрим площадку с нормалью 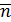 , взятую в окрестности некоторой точки деформируемого тела (рис. П1.4). Полное напряжение в общем случае не совпадает с направлением нормали. Его проекции на направление нормали
, взятую в окрестности некоторой точки деформируемого тела (рис. П1.4). Полное напряжение в общем случае не совпадает с направлением нормали. Его проекции на направление нормали 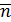 и касательной обозначим соответственно
и касательной обозначим соответственно 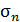 и
и 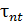 , тогда
, тогда
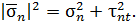
| 
|
Рис. П1.4. Составляющие 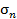 , , 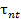 полного напряжения на элементарной площадке полного напряжения на элементарной площадке
| Рис. П1.5. Проекции полного напряжения 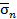 на координатные оси на координатные оси 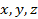
|
Если нормаль к площадке составляет с координатными осями 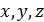 углы
углы 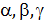 , то нормальную составляющую напряжений
, то нормальную составляющую напряжений 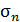 можно найти через проекции полного напряжения на координатные оси
можно найти через проекции полного напряжения на координатные оси 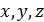 (рис. П1.5)
(рис. П1.5)
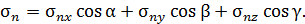
При повороте площадки напряжение в окрестности точки деформированного тела изменяется.
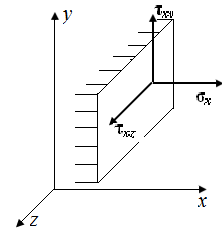
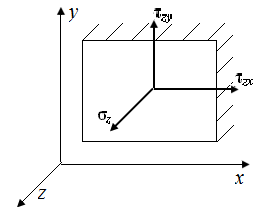
Для полной характеристики напряженного состояния в окрестности точки тела необходимо знать напряжения на трех взаимно перпендикулярных площадках, проведенных через эту точку (рис. П1.6). Девять напряжений 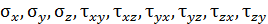 – составляющие полных напряжений, действующих на трех ортогональных площадках в окрестности точки твердого деформированного тела.
– составляющие полных напряжений, действующих на трех ортогональных площадках в окрестности точки твердого деформированного тела.
Если внешняя нормаль к площадке совпадает с положительным направлением оси координат, то положительные составляющие напряжений направлены в положительную сторону осей координат. Если внешняя нормаль к сечению направлена в сторону, противоположную положительному направлению оси координат, то положительные составляющие напряжений направлены в стороны, противоположные соответствующим направлениям осей координат.
| 
| 
|
| Рис. П1.6. Составляющие напряжений | ||
Напряженное состояние в окрестности тела характеризуется девятью составляющими напряжений, которые обычно записывают в виде тензора напряжений
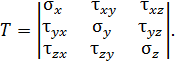
Выделим в твердом теле точку А (рис. П1.7). Пусть под действием внешних сил эта точка займет положение 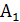 . Отрезок AB называют вектором полного упругого перемещения
. Отрезок AB называют вектором полного упругого перемещения 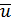 . Проекции вектора полного упругого перемещения на оси декартовой системы координат х, у, z обозначают
. Проекции вектора полного упругого перемещения на оси декартовой системы координат х, у, z обозначают 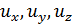 и называют составляющими перемещений точки.
и называют составляющими перемещений точки.
Различают два вида деформации тела: относительное удлинение в окрестности точки и относительный сдвиг.
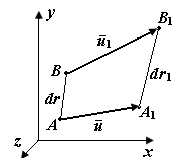
Величина 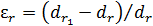 (рис. П1.7) - относительное удлинение в окрестности точки
(рис. П1.7) - относительное удлинение в окрестности точки 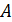 по направлению
по направлению 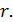 Относительное удлинение будем считать положительным, если бесконечно малые отрезки увеличиваются по длине.
Относительное удлинение будем считать положительным, если бесконечно малые отрезки увеличиваются по длине.
| 
|
| Рис. П1.7. Удлинения в окрестности точки А твердого тела в направлении r | Рис. П1.8. Изменение прямого угла в окрестности точки А при деформации твердого тела |
Рассмотрим прямой угол, образованный в недеформированном теле двумя отрезками AB и АС (рис. П1.8). После нагружения тела внешними силами этот угол изменяется, принимая значение  . Величину, равную изменению прямого угла после нагружения между двумя взаимно перпендикулярными направлениями называют относительным сдвигом, углом сдвига или просто сдвигом. Относительный сдвиг считается положительным, если прямой угол уменьшается.
. Величину, равную изменению прямого угла после нагружения между двумя взаимно перпендикулярными направлениями называют относительным сдвигом, углом сдвига или просто сдвигом. Относительный сдвиг считается положительным, если прямой угол уменьшается.
Относительные линейные и угловые деформации в направлении координатных осей х, у, z обозначают 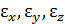 , а изменение углов между этими отрезками –
, а изменение углов между этими отрезками – 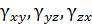 . Величины
. Величины 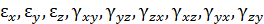 называют составляющими деформации в окрестности точки деформируемого твердого тела. Составляющие деформаций принято записывать в виде тензора, деформации
называют составляющими деформации в окрестности точки деформируемого твердого тела. Составляющие деформаций принято записывать в виде тензора, деформации
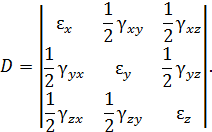
Перемещения и деформации зависят от координат точки тела, а напряжения – от координат точки, через которую проходит площадка (сечение), и от ориентации этой площадки. Составляющие напряжений и деформаций характеризуют напряженно-деформированное состояние точки твердого тела.
Три взаимно перпендикулярных нормальных напряжения, действующие в окрестности точки на площадке, на которых отсутствуют касательные напряжения, называют главными напряжениями:
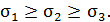
Три взаимно перпендикулярных направления, между которыми отсутствуют углы сдвига, называют главными осями деформации. Относительные удлинения 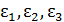 вдоль этих осей называют главными относительными удлинениями.
вдоль этих осей называют главными относительными удлинениями.
В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между нормальным напряжением 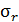 и относительным удлинением
и относительным удлинением 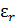
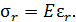
Коэффициент пропорциональности 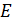 – модуль нормальной упругости – характеризует свойство материала элемента конструкции сопротивляться деформации растяжения.
– модуль нормальной упругости – характеризует свойство материала элемента конструкции сопротивляться деформации растяжения.
Коэффициент пропорциональности между касательным напряжением и относительным сдвигом – модуль упругости при сдвиге G – характеризует свойство материала элемента конструкции сопротивляться сдвигу одного слоя материала конструкции относительно другого.
Взятое по модулю отношение поперечного относительного сжатия тела к относительному удлинению в пределах соблюдения закона Гука называют коэффициентом Пуассона 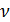 .
.
Величины E и G выражают в Паскалях (Па).
Модуль нормальной упругости E , модуль упругости при сдвиге G и коэффициент Пуассона 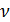 определяют экспериментально.
определяют экспериментально.
Удлинение 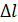 твердого тела длиной l связано с воздействием температуры соотношением
твердого тела длиной l связано с воздействием температуры соотношением
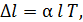
где 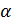 – температурный коэффициент линейного расширения.
– температурный коэффициент линейного расширения.
Если относительное перемещение элементов изделия происходит без деформации, то такую конструкцию называют геометрически изменяемой; если оно происходит только при деформации элементов – геометрически неизменяемой.
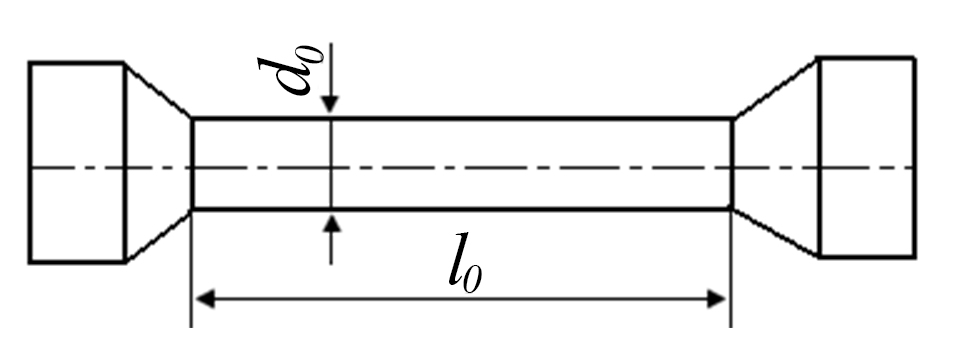
При определении механических свойств конструкционных материалов проводят испытания на растяжение, сжатие, кручение и изгиб образцов, форма и размеры которых стандартизированы (рис. П1.9).
|
| Рис. П1.9. Схема стандартизованного стержня |
Испытания на растяжения выполняют на разрывной машине при нагружении вдоль продольной оси стандартного образца диаметром 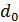 и рабочей частью
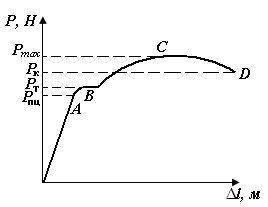
и рабочей частью 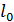 . На рис. П1.10 приведены диаграммы растяжения для пластичного и хрупкого образцов:
. На рис. П1.10 приведены диаграммы растяжения для пластичного и хрупкого образцов:
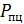 – максимальная нагрузка до которой зависимость между нагрузкой
– максимальная нагрузка до которой зависимость между нагрузкой 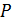 и удлинением образца линейна;
и удлинением образца линейна;
а
| б
|
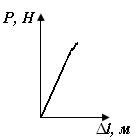
| Рис. П1.10. Диаграммы растяжения для пластичного (а) и хрупкого (б) образцов | |
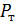 – нагрузка, при которой деформация образца происходит без ее увеличения (стадия текучести материала). После стадии текучести наступает стадия упругости материала. На диаграмме участок до точки С.
– нагрузка, при которой деформация образца происходит без ее увеличения (стадия текучести материала). После стадии текучести наступает стадия упругости материала. На диаграмме участок до точки С.
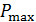 – максимальная нагрузка, которую испытывает образец, по достижении которой, деформация локализуется в ослабленном сечении образца.
– максимальная нагрузка, которую испытывает образец, по достижении которой, деформация локализуется в ослабленном сечении образца.
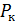 – нагрузка в момент разрушения образца.
– нагрузка в момент разрушения образца.
Для суждения о свойствах материала образца строят диаграмму условных напряжений (рис. П1.11) в системе координат 
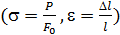 , F0 – первоначальная площадь поперечного сечения образца.
, F0 – первоначальная площадь поперечного сечения образца.
Вычисляют значения механических характеристик материала: характеристик прочности, определяющих способность материала сопротивляться нагрузкам, и характеристик пластичности, определяющих способность материала сопротивляться деформации. Характеристики прочности: предел пропорциональности 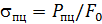 – напряжение, для которого справедлив закон Гука; предел текучести
– напряжение, для которого справедлив закон Гука; предел текучести 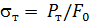 – напряжение,
– напряжение,
при котором деформации растут без заметного увеличения нагрузки (или составляют 0,2% от длины рабочей части образца); временное сопротивление 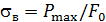 – напряжение, соответствующее максимальной нагрузке, предшествующей разрушению образца; истинное напряжение в момент разрыва
– напряжение, соответствующее максимальной нагрузке, предшествующей разрушению образца; истинное напряжение в момент разрыва 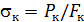 . Характеристики пластичности: относительное удлинение
. Характеристики пластичности: относительное удлинение
после разрыва, %:
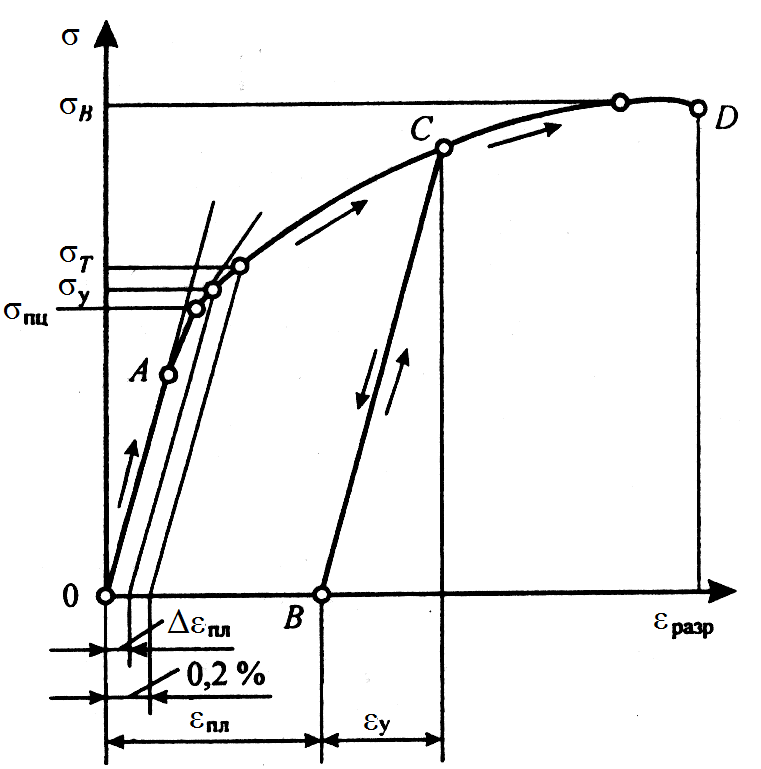
|
| Рис. П1.11. Диаграмма условных нагружений |
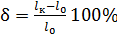 ,
,
относительное сужение поперечного сечения образца после разрыва
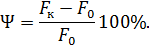
Относительное удлинение e произвольной точки С представляет сумму упругой 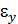 и пластической
и пластической 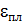 деформации. После разгрузки образца упругая деформация
деформации. После разгрузки образца упругая деформация 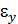 исчезает, а пластическая
исчезает, а пластическая 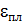 остается.
остается.
Для избежания образования в элементах конструкций заметных остаточных напряжений, за величину опасного напряжения 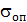 для пластичных материалов принимается обычно предел текучести
для пластичных материалов принимается обычно предел текучести 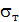 .
.
Для хрупких, а в некоторых случаях и умеренно пластичных материалов за 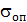 принимают временное сопротивление
принимают временное сопротивление 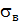 .
.
Расчет напряжений ведется по наибольшему напряжению 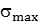 , возникающему в некоторой точке нагруженного тела.
, возникающему в некоторой точке нагруженного тела.
Искомые размеры элемента конструкции получают из условия
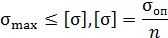
где 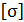 – допускаемое напряжение, n – коэффициент запаса.
– допускаемое напряжение, n – коэффициент запаса.
Пример П1.1. Какие возможности при решении задач дает введение допущений сплошности, однородности и изотропности материала конструкций?
Допущение о сплошности материала элемента конструкции позволяет пользоваться методом анализа бесконечно малых (интегрировать, дифференцировать). Оно приемлемо лишь для тел, размеры которых существенно превышают межатомные расстояния.
Допущение однородности материала допускает, что его свойства (физические и механические) неизменны в пределах рассматриваемой области.
|
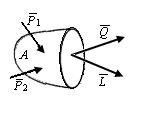
| Рис. П1.12. Главный вектор внутренних сил и вектор главного момента внутренних сил на схеме поперечного сечения стержня |
Допущение анизотропности позволяет считать, что физические и механические свойства не зависят от угловой ориентации элемента конструкции.
Пример П1.2. На какие составляющие раскладываются приведенные к центру тяжести сечения главный вектор внутренних сил и вектор главного момента внутренних сил (рис. П.1.12). Как их называют?
При деформации твердого тела нарушается взаимодействие между его частицами. Это приводит к появлению внутренних сил. Для определения этих сил используют метод сечений. При этом внутренние силы можно представить главным вектором внутренних сил 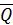 и вектором главного момента
и вектором главного момента 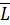 (рис. П1.13, а).
(рис. П1.13, а).
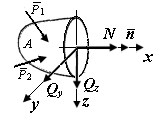
Для удобства вычислений эти векторы раскладывают на составляющие:
а) главный вектор сил на нормальную силу 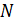 и поперечные силы
и поперечные силы 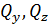 (рис. П1.13, а);
(рис. П1.13, а);
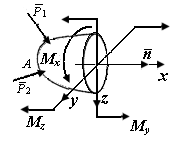
б) вектор главного момента на три пары сил с крутящим моментом  и двумя изгибающими моментами
и двумя изгибающими моментами  и
и 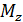 (рис. П1.13, б).
(рис. П1.13, б).
а
| б
|
| Рис. П1.13. Составляющие главного вектора внутренних сил (а) и вектора главного момента внутренних сил (б) | |
П6. Расчет перемещений
При инженерных расчетах перемещений в стержне с постоянной изгибной жесткостью 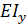 и одним грузовым участком используют полученное при чистом изгибе (
и одним грузовым участком используют полученное при чистом изгибе ( 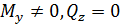 ) приближенное дифференциальное уравнение изогнутой оси стержня
) приближенное дифференциальное уравнение изогнутой оси стержня

где 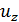 – перемещение по направлению оси z в окрестности точки, через которую проходит поперечное сечение, нагруженное изгибающим моментом
– перемещение по направлению оси z в окрестности точки, через которую проходит поперечное сечение, нагруженное изгибающим моментом  .
.
При кручении стержня с постоянной жесткостью 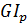 (G – модуль упругости при сдвиге,
(G – модуль упругости при сдвиге, 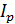 – полярный момент инерции), угол поворота определяют используя дифференциальное уравнение угла закручивания поперечного сечения стержня
– полярный момент инерции), угол поворота определяют используя дифференциальное уравнение угла закручивания поперечного сечения стержня

Формула угла закручивания 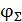 для стержня, имеющего n участков с различными механическими характеристиками материала на каждом i-м участке, при постоянных, в пределах каждого участка, значениях момента
для стержня, имеющего n участков с различными механическими характеристиками материала на каждом i-м участке, при постоянных, в пределах каждого участка, значениях момента  , имеет следующий вид:
, имеет следующий вид:
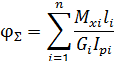
Условие жесткости при кручении стержня характеризуется выражением
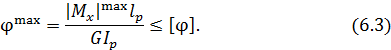
где 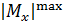 – наибольший по модулю на эпюре
– наибольший по модулю на эпюре  крутящий момент;
крутящий момент; 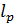 – расчетная длина, на которой определяют угол закручивания;
– расчетная длина, на которой определяют угол закручивания; 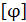 – допустимый на данной длине угол закручивания.
– допустимый на данной длине угол закручивания.
Для упрощения вычислений перемещений разработано несколько методов.
Метод начальных параметров.
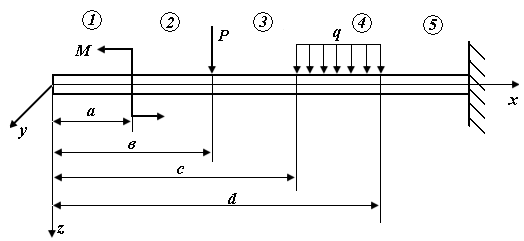
Предположим, стержень (рис. П6.1, а) нагружен сосредоточенным моментом М, приложенным на расстоянии а от левого конца стержня, силой Р на расстоянии b и распределенной нагрузкой q на расстоянии с от начала отсчета. Чтобы обеспечить равенство всех постоянных интегрирования на границах грузовых участков, при составлении дифференциальных уравнений упругой линии и их интегрировании соблюдают следующие правила:
а
|
б
|
в
|
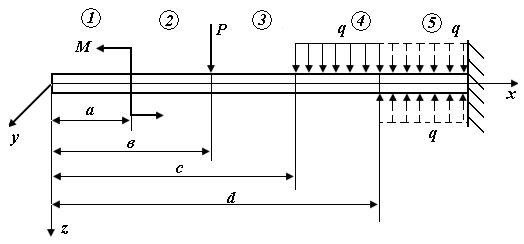
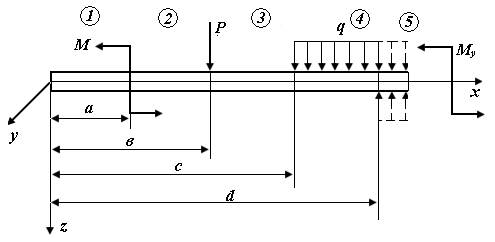
| Рис. П6.1. Схема стержня, нагруженного в плоскости xOz |
1) начало координат выбирают в крайней левой точке стержня;
2) выражение для изгибающего момента  составляют применительно к левой отсеченной части стержня;
составляют применительно к левой отсеченной части стержня;
3) сосредоточенный момент М домножают на 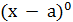 , что равно единице;
, что равно единице;
4) распределенную нагрузку продлевают до конца рассматриваемого сечения, а чтобы общий характер внешнего воздействия не изменился, прикладывают «компенсирующую» нагрузку обратного направления (рис. П6.1, б);
5) уравнения для всех участков интегрируют, не раскрывая скобок.
Если на стержень действуют несколько сосредоточенных моментов, сил и распределенных нагрузок, выражения для перемещений и углов поворота в произвольном сечении можно представить в следующем виде:
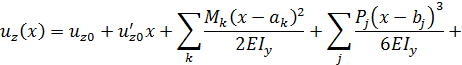
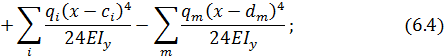
Эти выражения называют универсальными уравнениями упругой линии стержня.
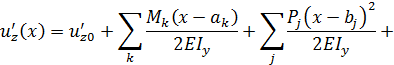
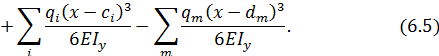
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ…………………………………………………………………… | 3 |
| ЗАДАЧИ………………………………………………………………………. | 3 |
| 1. Основные понятия прикладной механики……………………………. | 3 |
| 2. Закрепление стержней. Опорные реакции…………………………….. | 5 |
| 3. Определение внутренних усилий в стержнях…………………………. | 6 |
| 4. Основные уравнения механики твердого деформированного тела….. | 7 |
| 5. Расчет напряжений и анализ прочности стержней……………………. | 10 |
| 6. Расчет перемещений……………………………………………………. | 13 |
| 7. Определение динамических параметров при ударе………………….. | 16 |
| РЕШЕНИЕ ЗАДАЧ…………………………………………………………... | 17 |
| 1. Основные понятия прикладной механики…………………………….. | 17 |
| 2. Закрепление стержней. Опорные реакции…………………………….. | 20 |
| 3. Определение внутренних усилий в стержнях…………………………. | 23 |
| 4. Основные уравнения механики твердого деформированного тела….. | 25 |
| 5. Расчет напряжений и анализ прочности стержней……………………. | 30 |
| 6. Расчет перемещений……………………………………………………. | 36 |
| 7. Определение динамических параметров при ударе………………….. | 40 |
| ПРИЛОЖЕНИЕ………………………………………………………………. | 42 |
| П1. Основные понятия прикладной механики………………………….. | 42 |
| П2. Закрепление стержней. Опорные реакции…………………………... | 52 |
| П3. Определение внутренних усилий в стержнях………………………. | 56 |
| П4. Основные уравнения механики твердого деформированного тела.. | 60 |
| П5. Расчет напряжений и анализ прочности стержней…………………. | 67 |
| П6. Расчет перемещений………………………………………………….. | 77 |
| П7. Определение динамических параметров при ударе……………….. | 81 |
Бегун Петр Иосифович
Лебедева Елена Александровна
Лобачева Дарья Александровна
Задачи прикладной механики
Электронное учебное пособие
Редактор
Подписано в печать. Формат 60×84 1/16.
Бумага офсетная. Печать цифровая. Печ. л. 3
Гарнитура «TimesNewRoman».
Издательство СПбГЭТУ «ЛЭТИ»
ЗАДАЧИ ПРИКЛАДНОЙ МЕХАНИКИ
Электронное учебное пособие
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2017
УДК 531/534(07)
ББК ж 12я7
Б 37
Авторы: П. И. Бегун, Е. А. Лебедева, Д. А. Лобачева
Задачи прикладной механики: электронное учеб. пособие. СПб.:
Изд-во СПБГЭТУ «ЛЭТИ», 2017. 86 с.
ISBN978-5-7629-1688-2
Содержит два раздела и приложение: первый раздел с условиями задач и второй с их решениями. Задачи скомпонованы по следующим темам: 1. Основные понятия прикладной механики; 2. Закрепление стержней. Опорные реакции; 3. Определение внутренних усилий в стержнях; 4. Основные уравнения механики твердого деформированного тела; 5. Расчет напряжений и анализ прочности стержней; 6. Расчет перемещений; 7. Определение динамических параметров при ударе. Приложение содержит основные понятия по прикладной механике
Предназначено для бакалавров, обучающихся по направлениям 12.03.04, 12.03.01, 20.03.01.
УДК 531/534(07)
ББК ж 12я7
Б 37
Рецензенты: кафедра 24 СПбГУАП; д-р пед. наук, проф. А. В. Самсонова (НГУ им. П. Ф. Лесгафта, СПб).
Утверждено
редакционно-издательским советом университета
в качестве учебного пособия
ВВЕДЕНИЕ
Пособие содержит два раздела: первый раздел с условиями задач и второй с их решениями. Задачи скомпонованы по следующим темам: 1. Основные понятия прикладной механики; 2. Закрепление стержней. Опорные реакции; 3. Определение внутренних усилий в стержнях; 4. Основные уравнения механики твердого деформированного тела; 5. Расчет напряжений и анализ прочности стержней; 6. Расчет перемещений; 7. Определение динамических параметров при ударе.
Задачи построены так, чтобы при незначительной затрате времени при понимании материала темы, дать правильный ответ на поставленную задачу.
Задачи могут быть использованы при экспресс опросе студентов для выяснения степени усвоения материала. Приведенные решения задач дают возможность студенту проконтролировать свои умения в реализации полученных знаний при самостоятельной работе.
ЗАДАЧИ
Основные понятия прикладной механики
1.1. Какие возможности при решении задач механики дают три принципа: 1) принцип относительной жесткости; 2) принцип суперпозиции; 3) принцип Сен-Венана?
1.2. Какие возможности при решении задач дает введение допущений сплошности, однородности и изотропности материала конструкций?
1.3. На какие составляющие раскладываются приведенные к центру тяжести сечения главный вектор внутренних сил и вектор главного момента внутренних сил. Как их называют?
1.4. Какие правила знаков вводят для составляющих главного вектора внутренних сил?
1.5. Какие правила знаков вводят для составляющих вектора главного момента внутренних сил?
1.6. На рис. 1 показан элементарный прямоугольный параллелепипед и касательные напряжения 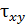 и
и 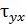 на его гранях. Допускаем, что нижняя грань параллелепипеда жестко закреплена. Указать углы сдвига и перемещения точек.
на его гранях. Допускаем, что нижняя грань параллелепипеда жестко закреплена. Указать углы сдвига и перемещения точек.
1.7. На рис. 2 приведена диаграмма, полученная при растяжении образца из пластичного материала. Допустим, что аналогичный образец нагрузили до величины, соответствующей точке D и стали разгружать. м
Как определить: 1) величины упругой и пластической деформации; 2) изменятся ли механические характеристики образца?

| 
|
| Рис. 1. Деформированный параллелепипед | Рис. 2. Диаграмма растяжения образца из пластичного материала |
1.8 Какая разница между силовыми факторами 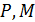 и внутренними силовыми факторами
и внутренними силовыми факторами 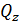 и
и  (рис. 3)?
(рис. 3)?
1.9. Опорные реакции (рис. 4) являются внутренними или внешними силами?

| 
|
| Рис. 3. Силовые факторы в сечении нагруженного стержня | Рис. 4. Нагруженный стержень |
1.10. Какие зависимости раскрывают условия статического равновесия?
1.11. Достаточно ли условий статического равновесия для определения опорных реакций в стержне, приведенном на рис. 5, а, б?
1.12. Как следует закрепить стержень (рис. 6), чтобы: 1) сечение, проходящее через точку А не могло перемещаться вдоль осей x и z и поворачиваться вокруг оси y; 2) сечения, проходящие через точки А и В не могли перемещаться вдоль осей x и z и поворачиваться в плоскости xOz; 3) сечения, проходящее через точку A не могло перемещаться вдоль осей x и z, а сечение, проходящее через точку B - вдоль оси z?
а

| б

|
| Рис. 5. Нагруженный стержень | |

|
Рис. 7. Стержень нагруженный в плоскости xOz |
| Рис. 6. Незафиксированный стержень | |
1.13. Каким свойством обладает материал стержня (Рис. 7), если после снятия нагрузки: 1) полностью восстанавливает свою первоначальную форму и размеры; 2) частично восстанавливает свою первоначальную форму и размеры; 3) сохраняет ту форму, которую получил при нагружении?
| а | б |

| 
|
| Рис. 8. Схемы стержней, нагруженных вдоль оси х и закрепленных по левому контуру | |
Закрепление стержней. Опорные реакции
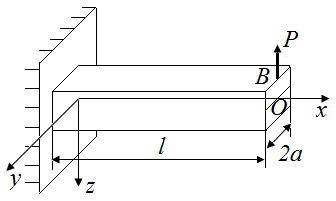
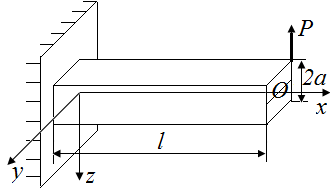
2.1. Какие опорные реакции возникают в стержнях, нагруженных в соответствии с рис. 8 и 9. Определить величины этих опорных реакций в стержне длиной l квадратного поперечного сечения со стороной 2a.
| а | б |
| 
|
| в | |
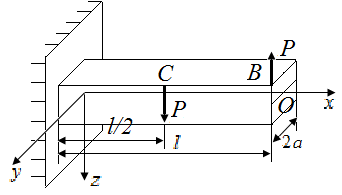
| Рис. 9. Схемы стержней, нагруженных вдоль оси z и закрепленных по левому контуру |
Дата: 2019-02-25, просмотров: 411.
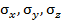 на трех взаимно перпендикулярных площадках
на трех взаимно перпендикулярных площадках