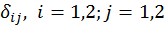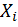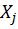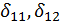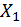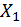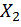Рассмотрим систему канонических уравнений (2). Как уже отмечалось, коэффициенты при неизвестных  – перемещения по направлению силы , вызванные единичной силой . Принято перемещения от единичных воздействий называть удельными перемещениями. В первом уравнении  – перемещения по направлению силы , вызванные соответственно единичными силами  и . Во втором уравнении 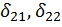– перемещения по направлению силы 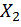, вызванные соответственно единичными силам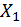и  и 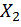. Свободные (или грузовые члены)  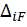,  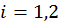 – перемещения по направлению силы 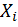, вызванные заданной нагрузкой.

Все перемещения находим методом Максвелла - Мора (перемножением соответствующих эпюр изгибающих моментов):

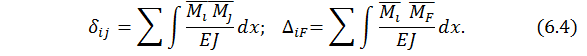
В формулах (6.4) интегрирование проводится в пределах длины участка перемножения, суммирование – по количеству таких участков.

Отметим два свойства коэффициентов при неизвестных.

1. Перемещения с одинаковыми индексами всегда положительны, не могут быть равны нулю, поэтому их называют главными (в данном примере это 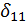 и ).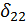

2. Коэффициенты с разными индексами называют побочными коэффициентами. На основании теоремы взаимности перемещений .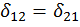

56

В выражениях (6.4) 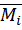 (или 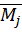) – эпюры изгибающих моментов, построенные в выбранной основной системе метода сил от единичных значений неизвестных;  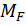– эпюра изгибающих моментов, построенная в ОСМС от заданной нагрузки.

Для проверки найденных коэффициентов и свободных членов канонических уравнений необходимо построить суммарную единичную эпюру 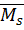 – эпюру от одновременного действия единичных значений неизвестных. Эпюра  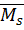 строится в выбранной ОСМС алгебраическим сложением единичных эпюр: 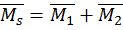. В общем случае можно записать 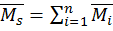, где n – степень статической неопределимости системы.

Рассмотрим способы проверки коэффициентов и свободных членов канонических уравнений метода сил.

1. Построчная проверка коэффициентов при неизвестных: алгебраическая сумма коэффициентов i - й строки равна результату перемножения i - й единичной эпюры изгибающих моментов на суммарную единичную эпюру изгибающих моментов:

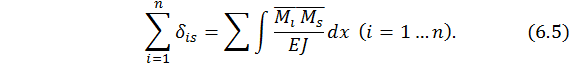
Например, для первой строки системы уравнений (6.5) (при i =1), имеем

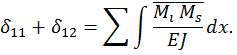
2. Универсальная проверка коэффициентов при неизвестных: алгебраическая сумма всех коэффициентов при неизвестных равна результату перемножения суммарной единичной эпюры изгибающих моментов самой на себя: 

57

                   .

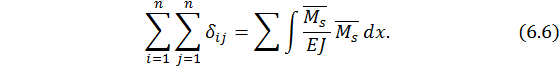В рассматриваемом примере с учетом равенства коэффициентов 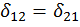будем иметь

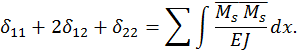
3. Проверка свободных (грузовых) членов: алгебраическая сумма грузовых членов равна результату перемножения грузовой эпюры 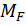 на суммарную единичную эпюру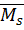

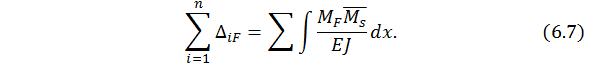
В правой части всех записанных выражений суммирование проводится по количеству участков перемножения, интегрирование – по длине каждого перемножаемого участка.

Выполнение проверок коэффициентов и свободных членов помогает обнаружить возможную ошибку на более ранней стадии расчета, поэтому их выполнение является желательным. Как правило, выполняют либо построчные проверки коэффициентов и проверку грузовых членов, либо универсальную проверку и также проверку грузовых членов.