Внецентренное сжатие в наибольшей степени интересно при использовании хрупких материалов. Как уже отмечалось ранее, для хрупких материалов расчетное сопротивление при сжатии не совпадает с расчетным сопротивлением при растяжении. В этом случае условие
22
прочности по нормальным напряжениям записывается в виде системы неравенств.
Определим опасные точки поперечного сечения. Очевидно (см. рис. 3.2), опасными являются точка 1 (в области сжатия) и точка 2 (в области растяжения), так как эти точки наиболее удалены от нейтральной линии. В точке 1 возникает наименьшее, а в точке 2 – наибольшее нормальные напряжения:
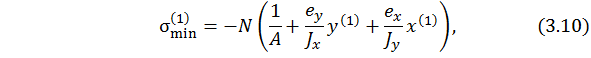
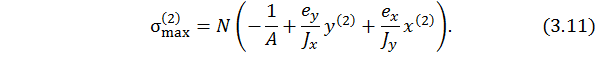
Тогда для указанных точек условие прочности принимает вид
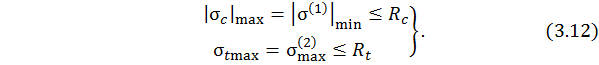
Можно рассмотреть напряжения от каждого отдельного вида внутреннего силового фактора: 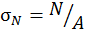 – нормальные напряжения при центральном сжатии;
– нормальные напряжения при центральном сжатии; 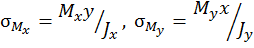 – нормальные напряжения при изгибе относительно осей x и y соответственно. Обратим внимание на очевидные зависимости при построении соответствующих эпюр напряжений. Напряжения
– нормальные напряжения при изгибе относительно осей x и y соответственно. Обратим внимание на очевидные зависимости при построении соответствующих эпюр напряжений. Напряжения 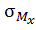 линейно зависят от координаты
линейно зависят от координаты 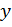 ; базисная линия эпюры
; базисная линия эпюры 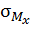 проводится параллельно оси
проводится параллельно оси 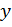 . Аналогично
. Аналогично 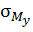 линейно зависят от координаты x; базисная линия эпюры
линейно зависят от координаты x; базисная линия эпюры 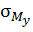 проводится параллельно оси x. Базисная линия эпюры
проводится параллельно оси x. Базисная линия эпюры 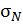 параллельна продольной оси рассматриваемого стержня (оси z), поэтому данную эпюру нужно показать для расчетной схемы заданного стержня, а не ограничиваться видом поперечного сечения.
параллельна продольной оси рассматриваемого стержня (оси z), поэтому данную эпюру нужно показать для расчетной схемы заданного стержня, а не ограничиваться видом поперечного сечения.
23
Замечание к расчету на прочность. Случаи сложного сопротивления можно разделить на две группы.
К первой группе относятся косой изгиб, внецентренное сжатие и внецентренное растяжение. Предполагается, что влияние возникающих в поперечных сечениях касательных напряжений невелико, поэтому расчет на прочность проводится без учета касательных напряжений и основан на рассмотрении нормальных напряжений в опасных точках поперечного сечения. Гипотезы прочности при этом не используются.
Ко второй группе относятся изгиб с кручением, сжатие или растяжение с кручением, сжатие или растяжение с кручением и изгибом одновременно. В этих случаях в поперечных сечениях возникают не только нормальные, но и касательные напряжения, причем значениями последних пренебрегать нельзя. Расчет на прочность проводится на основе гипотез прочности с учетом и нормальных, и касательных напряжений.
Глава 4. ЯДРО СЕЧЕНИЯ
Определение ядра сечения
Ядро сечения – выпуклая область вокруг центра тяжести сечения, обладающая свойством: если действующая сила приложена в ядре сечения, то нормальные напряжения во всех точках поперечного сечения имеют одинаковый знак. Знак нормальных напряжений определяется направлением действующей силы: если сила сжимающая, то напряжения отрицательные; если сила растягивающая, то напряжения положительные.
Известно, что многие строительные материалы (бетон, кирпич) плохо работают на растяжение, но хорошо выдерживают сжимающие нагрузки: 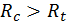 в несколько раз. Поэтому на практике ставится задача не допустить появления растягивающих напряжений в колоннах, выполненных из хрупких материалов. Этой задаче и служит построения ядра сечения в плоскости поперечного сечения.
в несколько раз. Поэтому на практике ставится задача не допустить появления растягивающих напряжений в колоннах, выполненных из хрупких материалов. Этой задаче и служит построения ядра сечения в плоскости поперечного сечения.
24
Свойства ядра сечения
1) Чем дальше от начала координат расположен полюс, т.е. чем больше по абсолютной величине эксцентриситеты 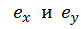 , тем ближе к центру тяжести проходит нейтральная линия. Это очевидно: с увеличением эксцентриситетов уменьшаются длины отрезков, которые нейтральная линия (НЛ) отсекает на главных центральных осях поперечного сечения, и наоборот.
, тем ближе к центру тяжести проходит нейтральная линия. Это очевидно: с увеличением эксцентриситетов уменьшаются длины отрезков, которые нейтральная линия (НЛ) отсекает на главных центральных осях поперечного сечения, и наоборот.
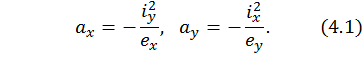
2) Если полюс расположен на одной из главных центральных осей инерции, то НЛ перпендикулярна этой оси. Докажем это.
| Рис. 4.1 |
| О |
| y |
| x |
| НЛ |
1-е положение. Пусть точка О находится на горизонтальной оси х. Очевидно, существует 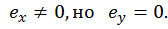 Тогда
Тогда
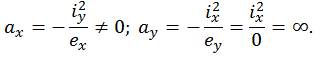
25
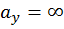 означает, что пересечение НЛ с осью у возможно только в бесконечности, т. е. НЛ параллельна вертикальной оси у.
означает, что пересечение НЛ с осью у возможно только в бесконечности, т. е. НЛ параллельна вертикальной оси у.
2-е положение. Пусть точка О находится на вертикальной оси у. Очевидно, существует 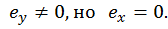 Тогда
Тогда
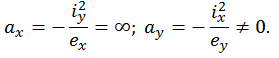
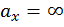 означает, что пересечение НЛ с осью x возможно только в бесконечности, т. е. НЛ параллельна горизонтальной оси x .
означает, что пересечение НЛ с осью x возможно только в бесконечности, т. е. НЛ параллельна горизонтальной оси x .
| y |
| О |
| x |
| НЛ |
Рис. 4.2
Дата: 2019-02-25, просмотров: 309.