Рассмотрим произвольный многоугольник, в котором оси yx – главные центральные оси.
| а5 |
| а5 |
| а4 |
| а4 |
| а3 |
| а3 |
| а 2 |
| а 2 |
| а 1 |
| а 1 |
| A5 |
| A4 |
| A3 |
| A2 |
| A1 |
| y |
| x |
Рис. 4.4
29
Каждому положению полюса соответствует строго определенное положение нейтральной линии.
Точка А1 – полюс, НЛ – а1 а1.
Точка А2 – полюс, НЛ – а2 а2.
Точка А3 – полюс, НЛ – а3 а3.
Точка А4 – полюс, НЛ – а4 а4.
Точка А5 – полюс, НЛ – а5 а5.
Например, при перемещении полюса по прямой а2 а2 НЛ вращается вокруг А2 по ходу часовой стрелки, занимая различные положения.
Порядок построения ядра сечения
1) Определить центр тяжести и главные центральные оси поперечного сечения.
2) Определить геометрические характеристики (площадь, осевые моменты инерции, квадраты радиусов инерции).
3) Если сечение имеет вид многоугольника (т.е. образовано отрезками прямых), то последовательно задаем положения НЛ, совпадающие с линией контура поперечного сечения.
В этом случае фактически известны отрезки, которые НЛ отсекает, поэтому по формулам (4.4) вычисляем координаты полюса, соответствующие конкретному положению НЛ.
4) Полученные точки полюса соединяем прямыми линиями.
Важно. Внутренние узлы поперечного сечения не рассматриваем.
| А |
| В |
| С |
| D |
| E |
| Рис. 4.5 |
30
5) Если сечение имеет кривые линии, то задают положение НЛ в нескольких точках, касательных к кривой. Полученные точки полюсов соединяют кривыми линиями.
Положений нейтральной линии необходимо задать столько, сколько потребуется для построения замкнутого многоугольника обхода контура поперечного сечения. Например, на рис. 4 пунктирными
линиями показаны возможные положения нейтральной линии для построения ядра сечения: линии AB, BC, CD, DE и АЕ. Обратим внимание: обход сечения проводится только по внешним точкам контура сечения. Соединяя точки полюса, полученные для каждого положения нейтральной линии, получим замкнутый многоугольник – ядро сечения. Заметим, если сечение симметричное, то ядро сечения также симметрично. Далее показаны примеры построения ядра сечения в широко распространенных сечения.
31
Глава 5. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Основные понятия
При сжатии стержня может наблюдаться не только потеря прочности, но и потеря устойчивости (выпучивание стержня). При этом несущая способность стержня вследствие потери устойчивости может быть исчерпана раньше, чем непосредственно от сжатия.
Проблема (задача) потери устойчивости возникает при осевом (центральном) сжатии гибкого достаточно длинного и тонкого стержня. Вспомним, что при осевом сжатии короткого стержня наблюдается деформация сжатия. Из теоретической механики известно, что равновесие твердых тел может быть устойчивым и неустойчивым. Упругое равновесие называется устойчивым, если при каком-либо внешнем воздействии система стремится вернуться в исходное положение. В случае неустойчивого равновесия система деформируется до полного разрушения. Замечание. В нашем курсе мы будем рассматривать потерю устойчивости отдельных стержней системы, а не потерю устойчивости системы стержней в целом.
Потерей устойчивости стержня называется его переход из первоначального положения равновесия к другому положению равновесия, то есть переход из одной равновесной формы в другую. Нагрузка, при которой происходит потеря устойчивости, называется критической. На рис. 5.1 показаны возможные положения стержня в зависимости от значения сжимающей силы. Обозначим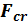 
– некоторое критическое значение сжимающей силы.
Критической силой принято называть наименьшее значение центрально приложенной силы, при котором прямолинейная форма равновесия становится неустойчивой. Для ответа на вопрос о состоянии стержня или стержневой системы с точки зрения потери устойчивости действующее значение сжимающей силы сравнивается с с критическим значением.
32
| F = F cr |
| б) |
| F < F cr |
| а) |
| F > F cr |
| в) |
| Рис. 5.1 |
Очевидно, стержень находится в состоянии устойчивого равновесия, если действующая сжимающая сила меньше некоторого критического значения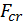 
– рис. 5.1, а.
Если сжимающая сила достигает критического значения, стержень отклоняется от вертикального положения; возникает состояние как бы безразличного равновесия: после отклонения стержень приобретает равновесие и в искривленном положении; при этом он не возвращается в первоначальное положение, но и не искривляется далее. Происходит бифуркация, то есть раздвоение состояния равновесия: прямолинейная форма теряет устойчивость, а криволинейная еще не успевает ее приобрести (см. рис. 5.1, б). Наконец, если действующая сила превышает критическое значение, то возникает новая криволинейная форма устойчивого равновесия (см. рис. 5.1, в). С практической точки зрения состояния, изображенные на рис. 5.1, б и 5.1, в, для строительных конструкций неприемлемы. Например, в последнем случае стержень работает не только на сжатие, но и дополнительно на изгиб: могут возникнуть недопустимо большие прогибы и напряжения даже при небольшом превышении критического значения.
33
§ 5.2. Формула Эйлера определения критической силы
Леонард Эйлер (Leonard Euler, 1707 – 1783) – величайший математик, физик, механик, астроном. Родился в Швейцарии, но более 30 лет жил в Петербурге; академик Петербургской Академии Наук.
Предварительно заметим, что существуют различные методы исследования устойчивости, которые рассматриваются в специальных курсах: например, известен курс «Устойчивость сооружений». Метод Эйлера является наиболее простым для решения задач инженерной практики. Метод основан на анализе разветвления возможных форм равновесия упругой системы. Повторим рассуждения Эйлера. Формула была выведена для случая шарнирного закрепления концов стержня (рис. 5.2), причем Эйлер доказал, что деформированная ось стержня (на рисунке показана тонкой линией) – полуволна синусоиды. В дальнейшем изогнутую ось стержня в случае потери устойчивости так и называют – полуволна синусоиды Эйлера.
| Рис. 5.2 |
| F |
 |
Известно приближенное дифференциальное уравнение упругой линии
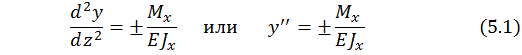
34
Справа в выражении (5.1) использовано распространенное обозначение производной штрихами; два штриха обозначают вторую производную: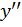 
= 
.
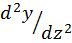Мы будем рассматривать принятую нами ранее систему координат (на рис. 5.2 она не показана): начало координат поместим в нижней опоре; вдоль стержня направим ось z вверх; перпендикулярно ей ось y влево от начала координат. Выбранной системе координат соответствует знак плюс в уравнениях (5.1):
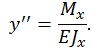
| (5.2) |
В правой части записанных выражений (5.1) и (5.2)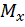 
– изгибающий момент в произвольном сечении балки на расстоянии 
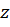от начала координат; 
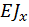– жесткость сечения балки при изгибе.
Замечание. Дифференциальное уравнение упругой линии можно использовать и при изучении устойчивости сжатых стержней, так как потеря устойчивости стержня возникает при малых деформациях, т. е. справедлива гипотеза о малости деформаций.
В произвольном сечении стержня (отсчет от начала координат) с абсциссой z изгибающий момент имеет значение
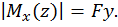
Тогда (5.2) перепишем с учетом выражения момента, дополнительно учтем правило знака между прогибом и второй производной прогиба:
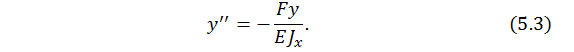
Обратим внимание: появился знак минус! Существует правило: прогиб (y) и вторая производная прогиба (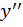 
) всегда разнозначны независимо от выбора положительного направления оси ординат.
35
Введем дополнительно обозначение:
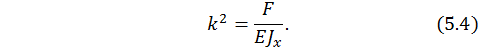
Тогда выражение (5.3) примет вид
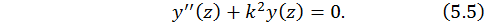
Получили однородное дифференциальное уравнение второго порядка. Общий интеграл этого уравнения (известно из высшей математики) представляет собой выражение вида
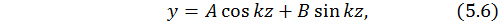
где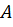 
и 
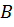– некоторые коэффициенты, которые можно найти из граничных условий по концам стержня.
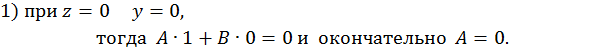
С учетом найденного значения для 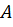выражение (5.6) принимает более простой вид:
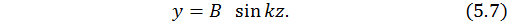
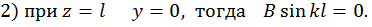Таким образом, получаем
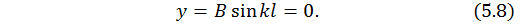
Уравнение (5.8) верно, если один из сомножителей равен нулю.
Если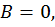 
то в выражении (5.6) заведомо 
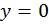, а это не соответствует условию задачи.
Очевидно, второй сомножитель должен быть равен нулю, т. е.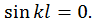 
36
Решением этого тригонометрического уравнения является
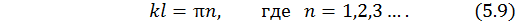
Возводим в квадрат обе части выражения (5.9), получим
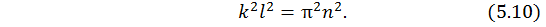
Отсюда выразим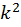 
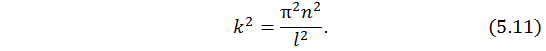
Вспомним о введенном ранее обозначении (5.4) и приравняем правые части (5.4) и (5.11), получим:
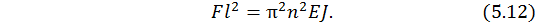
Выразим значение силы в виде
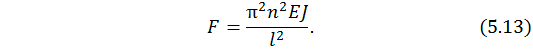
Таким образом, получили выражение критической силы в виде (5.13). Как видим из формулы, существует не одна, а множество значений критической силы в силу изменения параметра n. Очевидно, наименьшее значение критической силы имеем при минимальном значении n , т.е. при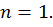 
Для прямых стержней известна формула Эйлера в виде
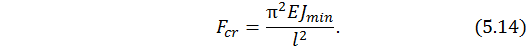
Здесь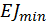 
– минимальная жесткость сечения стержня при изгибе; 
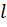– длина сжатого стержня.
37
Важно. Потеря устойчивости происходит в плоскости наименьшей жесткости!
Выводы. 1. Если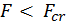 
, то возможна только прямолинейная форма равновесия, которая в этом случае является устойчивой.
2. Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости, но совершенно не зависит от прочностных характеристик материала стержня.
Далее на рис. 5.3 показаны возможные формы потери устойчивости при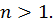 
(на рисунке изображены красными линиями)
Рис. 5.3
Дата: 2019-02-25, просмотров: 234.
